算法训练之BFS实现FloodFill算法

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥
♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥
♥♥♥我们一起努力成为更好的自己~♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥
✨✨✨✨✨✨个人主页✨✨✨✨✨✨
这一篇博客我们来学习新的算法,准备好了吗~我们发车去探索算法的奥秘啦~🚗🚗🚗🚗🚗🚗
目录
Flood Fill算法😜
什么是Flood Fill算法?😁
算法原理及步骤😊
三种实现方式👌
图像渲染😜
岛屿数量😜
岛屿的最大面积😜
被围绕的区域😜
Flood Fill算法😜
什么是Flood Fill算法?😁
Flood Fill,中文常译为“洪水填充”或“种子填充”算法,它是一种非常经典的区域填充算法。
它的核心思想非常直观,就像它的名字一样:
从一个起始点(种子点)开始,向四面八方(四向或八向)蔓延,将所有在指定区域内且相连的、颜色相同的点,都替换为新的颜色。这个过程就像一滴墨水滴在纸上,或者洪水漫过平原一样,因此得名。
一个最经典的类比就是 Windows 系统自带的“画图”软件里的【油漆桶】工具:你点击画布上的一个点,它就会把一片连续的同色区域全部填充为你新选择的颜色。
算法原理及步骤😊
Flood Fill算法的基本思路可以用以下步骤概括:
输入:一个起始点(x, y)、一种新的颜色、一个多维数组(通常代表图像或网格)。
目标:将起始点所在的连通区域(所有相连的、颜色相同的点)的颜色全部替换为新颜色。
过程:
检查起始点的颜色。如果它已经是新颜色,或者不是我们想要替换的旧颜色,则直接返回,无需操作。否则,将起始点的颜色改为新颜色。然后,递归地(或使用循环)对其邻接点(上、下、左、右,或者包括对角线)执行相同的操作。
三种实现方式👌
1. 递归实现 (DFS - 深度优先搜索)
核心思想: “一条路走到黑,再原路返回”。从一个点开始,选择一个方向前进,直到碰壁(遇到边界或不同颜色),然后退回上一个岔路口,选择另一个未探索的方向继续前进。
怎么做:从起点开始,给它上色, 立即对它的上、下、左、右四个邻居中的每一个,递归地调用自己。每个被调用的函数又做同样的事:上色,然后递归调用自己的邻居。
优点:代码非常简洁,最直观,最容易理解和实现。
缺点:非常危险! 对于大面积区域,递归层级会非常深,极易导致栈溢出(Stack Overflow),导致程序崩溃。不适用于生产环境。
比喻:像是一个执着的人,遇到一个岔路口就选一条路一直走下去,走到底后再返回到上一个岔路口换另一条路。
2. 迭代+栈实现 (DFS - 深度优先搜索)
核心思想: “用便签纸记录待办任务”。我们用一个栈(Stack)这种数据结构来模拟递归的过程,但避免了函数调用带来的开销和深度限制。
怎么做:
1、准备一张“便签纸”(栈),把起点写上去。
2、只要便签纸上还有任务:拿起最上面那张便签(弹出栈顶),去那个点上色。把这个点的上、下、左、右四个邻居地址,只要它们符合条件(是旧颜色且未越界),就写成新的便签纸压到栈顶。
3、重复步骤2。
优点:解决了递归方法的栈溢出问题,性能更好。保持了深度优先的搜索特性。
缺点:代码比递归稍长一些。
比喻:你有一个待探索地点的清单(栈)。你总是先去清单上最后一个加入的地点,处理完后把它邻居中新发现的地点加到清单末尾。这是最推荐的DFS实现方式。
3. 迭代+队列实现 (BFS - 广度优先搜索)
核心思想: “一圈一圈地向外扩张”。我们用一个队列(Queue)来保证先处理 older 的点,再处理 newer 的点,从而实现层层扩散的效果。
怎么做:
1、准备一个“待办队列”,把起点加入队列。
2、只要队列不为空:取出队列最前面的那个点(先进先出),去上色。把这个点的上、下、左、右四个邻居地址,只要符合条件,就追加到队列的末尾。
3、重复步骤2。
优点:同样避免了递归的栈溢出问题, 它以起点为中心均匀地向外扩散,在某些应用上更符合直觉(比如扫雷打开空白区域)。
缺点:通常需要存储的中间节点数量略多于栈实现,但非常可靠。
比喻:像一滴墨水滴入水中产生的波纹,一圈一圈地、均匀地向外扩散。这是最常用和最可靠的工业级实现方法。
总结对比
| 特性 | 递归DFS | 迭代栈(DFS) | 迭代队列(BFS) |
|---|---|---|---|
| 数据结构 | 函数调用栈 | 栈 (Stack) | 队列 (Queue) |
| 处理顺序 | 深度优先 | 深度优先 (后进先出) | 广度优先 (先进先出) |
| 空间风险 | 高 (易栈溢出) | 低 | 低 |
| 代码简洁性 | 非常简洁 | 简洁 | 简洁 |
| 推荐度 | 不推荐,仅用于学习 | 推荐 | 最推荐 |
结论:在实际编程中,应优先选择使用队列(BFS)或栈(DFS)的迭代实现,避免使用递归。
这一篇博客我们就是使用BFS实现这个Flood Fill算法~
图像渲染😜
图像渲染
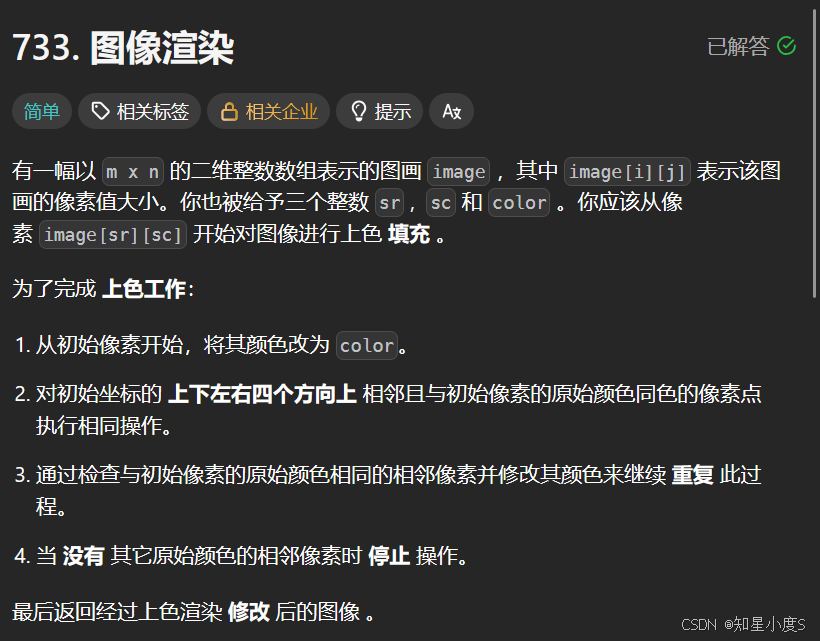
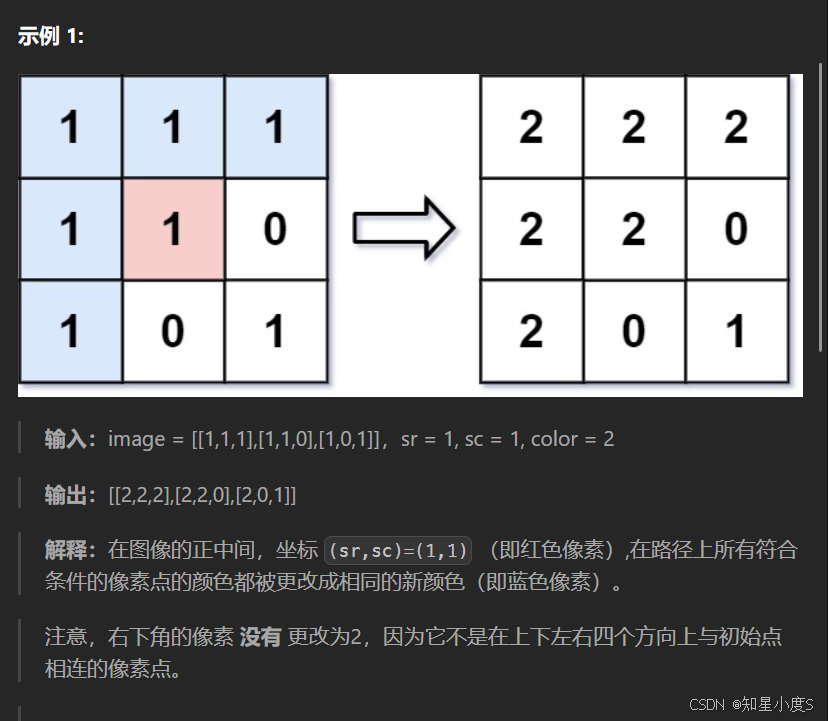
这个题目显然就需要用到我们的Flood Fill算法~
结合前面提到的实现方式,相信在这里这道题目是小菜一碟了~
算法思路:
边界情况处理:如果起始像素的颜色已经等于目标颜色,直接返回原图像(无需修改)。
初始化:
获取图像尺寸(行数 m 和列数 n)
记录起始像素的原始颜色(prev)
创建访问标记数组(vis)和队列(BFS所需)
广度优先搜索(BFS):
1、将起始像素加入队列,修改其颜色,并标记为已访问
2、从队列中取出像素,检查其上下左右四个方向的相邻像素
3、如果相邻像素在图像范围内、颜色与原始颜色相同且未被访问过,则将其加入队列并着色记录被访问
终止条件:当队列为空时,表示所有相连的相同颜色像素都已处理完毕
代码实现:
//图像渲染
class Solution
{typedef pair<int, int> PII;//类型更加简洁//两个数组对应四个方向int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };public:vector<vector<int>> floodFill(vector<vector<int>>& maze, int sr, int sc, int color){//处理边界情况if (maze[sr][sc] == color)return maze;//统计行列int m = maze.size();int n = maze[0].size();//记录原来的颜色int prev = maze[sr][sc];int vis[51][51] = { 0 };//记录位置是否被访问queue<PII> q;//队列保存//起点入队列q.push({ sr,sc });maze[sr][sc] = color;//修改颜色vis[sr][sc] = 1;//起点已经被访问while (q.size()){auto [qx, qy] = q.front();//取队头元素坐标q.pop();//对周围满足条件的进行上色for (int i = 0; i < 4; i++){int cx = qx + dx[i], cy = qy + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && maze[cx][cy] == prev && !vis[cx][cy]){q.push({ cx,cy });//入队列maze[cx][cy] = color;//修改为需要的颜色vis[cx][cy] = 1;//标记为被访问}}}//返回修改后的结果return maze;}
};
顺利通过~
岛屿数量😜
岛屿数量
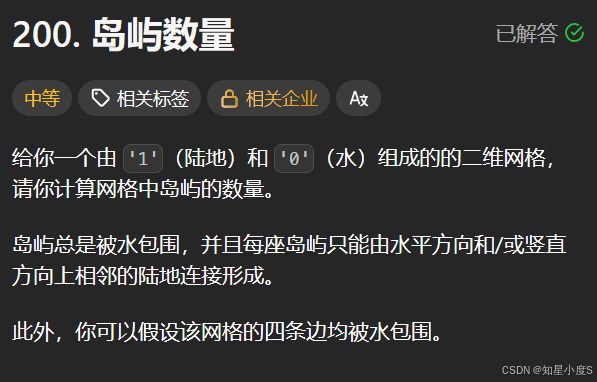
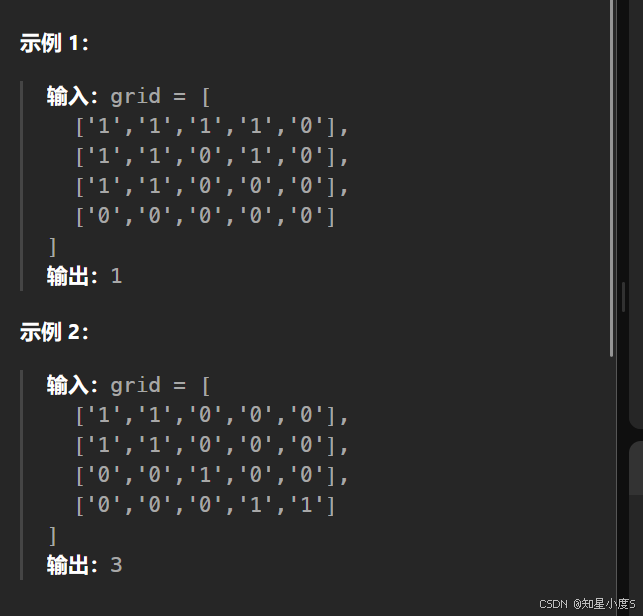
这一个题目和前面的又有一些不一样,不是进行修改颜色,需要我们求联通块的数量,这里我们就需要增加一个返回值了~
算法思路
遍历网格:逐个检查网格中的每个单元格。
发现岛屿:当遇到一个未被访问的陆地单元格('1')时,表示发现了一个新岛屿,计数器增加。
标记连通区域:通过 BFS 标记所有与该陆地单元格相连的陆地单元格(上下左右方向),确保整个岛屿被标记为已访问。
继续搜索:重复上述过程,直到所有单元格都被处理完毕。
代码实现:
//岛屿数量
class Solution
{typedef pair<int, int> PII;//类型更加简洁//两个数组对应四个方向int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };int m = 0, n = 0;//全局变量统计行列——函数都可以用int vis[301][301] = { 0 };//全局数组统计是否被访问——函数都可以用
public:int numIslands(vector<vector<char>>& grid){m = grid.size();n = grid[0].size();int count = 0;//记录联通块的数量for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (grid[i][j] == '1' && !vis[i][j]){count++;//联通块数量++bfs(grid, i, j);//标记联通块}}}return count;}void bfs(vector<vector<char>>& grid, int i, int j){queue<PII> q;q.push({ i,j });vis[i][j] = 1;while (q.size()){auto [qx, qy] = q.front();q.pop();for (int k = 0; k < 4; k++){int cx = qx + dx[k], cy = qy + dy[k];if (cx >= 0 && cx < m && cy >= 0 && cy < n && grid[cx][cy] == '1' && !vis[cx][cy]){q.push({ cx,cy });//是联通块内的入队列vis[cx][cy] = 1;//标记被访问}}}}
};
顺利通过~
岛屿的最大面积😜
岛屿的最大面积
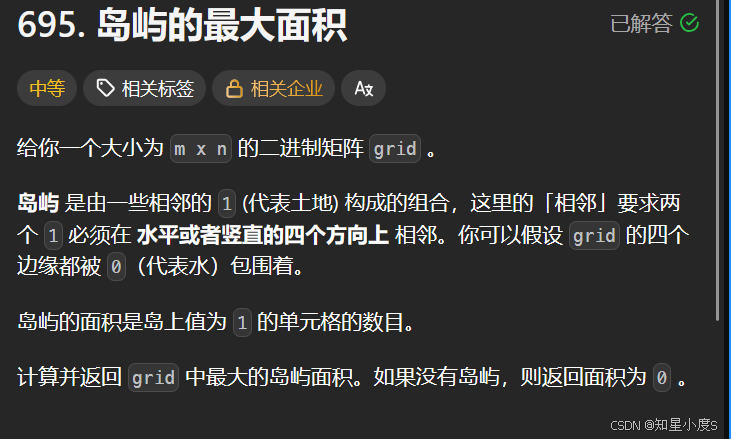
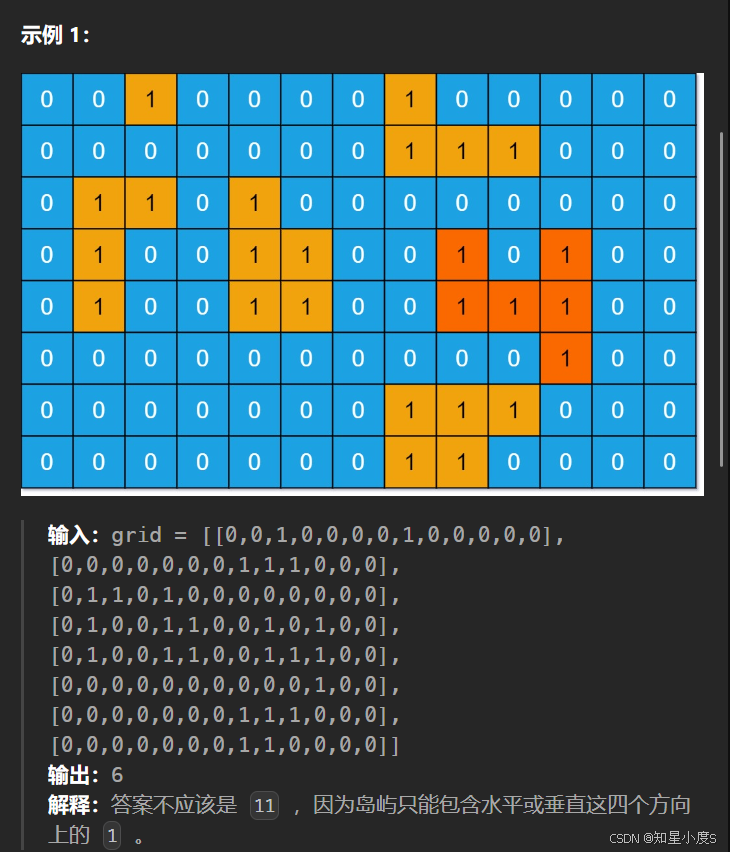
这一道题目和前面的题目有些类似,不同的是这一个题目需要找到的是最大面积,所以需要及时更新最大面积~
算法思路:
遍历网格:逐个检查每个单元格
发现新岛屿:当遇到值为1且未被访问过的单元格时,开始BFS
探索岛屿:从起点出发,探索所有相邻的陆地单元格
统计面积:在BFS过程中计数访问到的陆地单元格数量
更新最大值:比较当前岛屿面积与历史最大值
代码实现:
//岛屿的最大面积
class Solution
{typedef pair<int, int> PII;int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };int m = 0, n = 0;int vis[51][51] = { 0 };//记录是否被访问
public:int maxAreaOfIsland(vector<vector<int>>& grid){//统计行列m = grid.size();n = grid[0].size();//记录结果int ret = 0;//按序BFS遍历找岛屿的最大面积for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (grid[i][j] && !vis[i][j]){ret = max(ret, bfs(grid, i, j));//更新结果}}}//返回结果return ret;}//使用bfs记录当前岛屿面积返回int bfs(vector<vector<int>> grid, int i, int j){int count = 0;//记录当前岛屿面积queue<PII> q;q.push({ i,j });vis[i][j] = 1;//当前位置记录被访问count++;//当前位置也算一个面积while (q.size()){auto [qx, qy] = q.front();q.pop();for (int k = 0; k < 4; k++){int cx = qx + dx[k], cy = qy + dy[k];if (cx >= 0 && cx < m && cy >= 0 && cy < n && grid[cx][cy] && !vis[cx][cy]){//是当前位置周围的陆地入队列,计数++q.push({ cx,cy });count++;vis[cx][cy] = 1;//记录被访问}}}cout << count << endl;return count;}};
顺利通过~
被围绕的区域😜
被围绕的区域
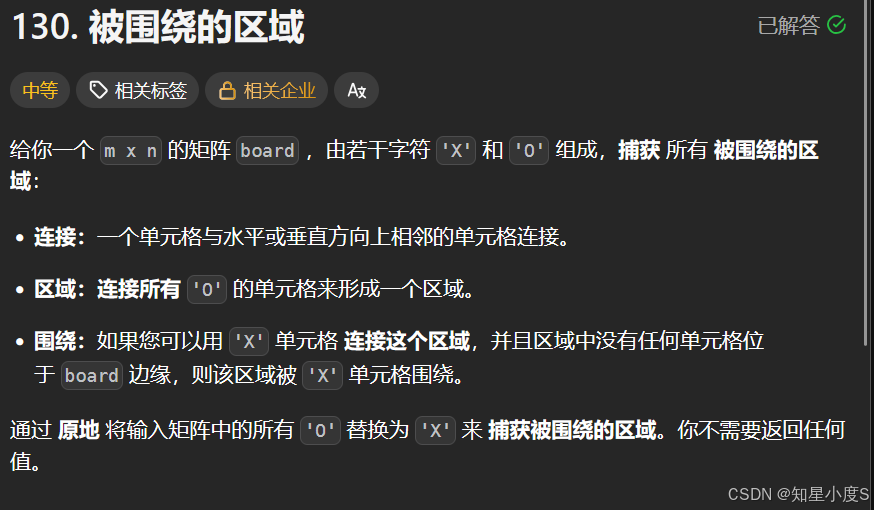

这道题目按照我们的常规思路是有点难解决的,因为到达边界的时候不好处理,那么我们就可以换一种思路,先处理边界的情况~
算法思路:
处理边界区域:遍历矩阵的四条边界(上、下、左、右),当遇到边界上的'O'时,开始标记与之相连的区域
标记连通区域:使用BFS/DFS遍历(这里使用BFS)所有与边界'O'相连的'O'单元格,将这些单元格标记为特殊字符(如'$'),表示它们不会被包围
转换字符:
遍历整个矩阵,将未被标记的'O'(即被围绕的区域)转换为'X',将特殊标记'$'恢复为原来的'O'
完成处理:
所有被围绕的区域已被正确捕获,矩阵修改完成
代码实现:
//被围绕的区域
class Solution
{typedef pair<int, int> PII;int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };int m = 0, n = 0;int vis[201][201] = { 0 };
public:void solve(vector<vector<char>>& board){m = board.size();n = board[0].size();//处理边界联通块!!!//边界'O'更换为字符$for (int i = 0; i < m; i++){if (board[i][0] == 'O')bfs(board, i, 0);if (board[i][n - 1] == 'O')bfs(board, i, n - 1);}for (int i = 0; i < n; i++){if (board[0][i] == 'O')bfs(board, 0, i);if (board[m - 1][i] == 'O')bfs(board, m - 1, i);}//遍历修改和还原字符for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){//修改if (board[i][j] == 'O')board[i][j] = 'X';//还原边界联通块else if (board[i][j] == '$')board[i][j] = 'O';}}}void bfs(vector<vector<char>>& board, int i, int j){queue<PII> q;q.push({ i,j });vis[i][j] = 1;board[i][j] = '$';while (q.size()){auto [qx, qy] = q.front();q.pop();for (int k = 0; k < 4; k++){int cx = qx + dx[k], cy = qy + dy[k];if (cx >= 0 && cx < m && cy >= 0 && cy < n && board[cx][cy] == 'O' && !vis[cx][cy]){q.push({ cx,cy });vis[cx][cy] = 1;board[cx][cy] = '$';//修改字符}}}}
};
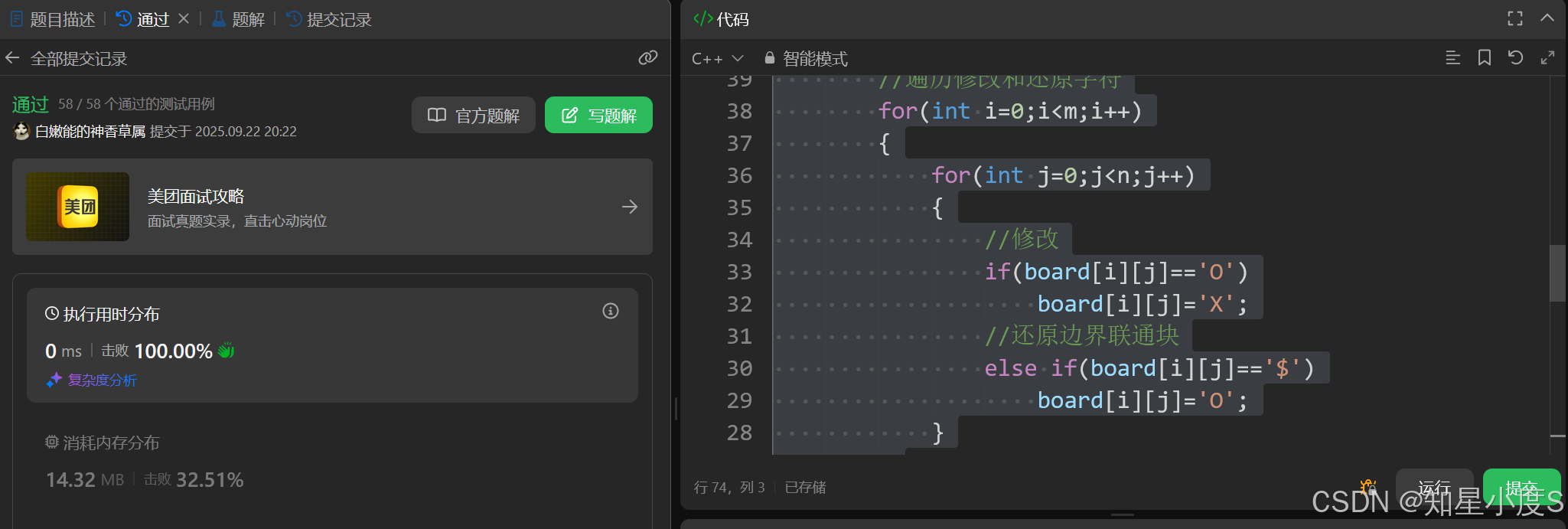
顺利通过~
♥♥♥本篇博客内容结束,期待与各位优秀程序员交流,有什么问题请私信♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
✨✨✨✨✨✨个人主页✨✨✨✨✨✨
