当前位置： 首页 > news >正文

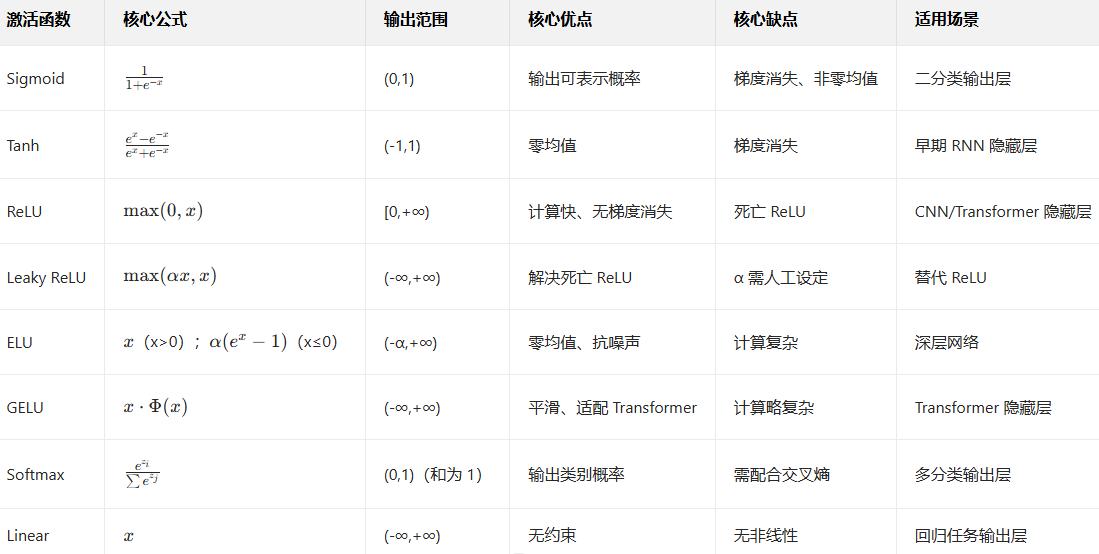
神经网络常用激活函数公式

news 2025/10/13 6:53:32

激活函数是神经网络的核心组件，负责为模型引入非线性能力，使其能够拟合复杂的数据分布（若没有激活函数，多层神经网络会退化为单层线性模型）。以下是深度学习中最常用的激活函数及其核心公式、特性与适用场景，按功能分类整理：

一、饱和激活函数（传统经典型）

“饱和” 指函数输出会趋近于固定值（如 0 或 1），早期神经网络中广泛使用，但因梯度消失问题逐渐被非饱和函数替代。

1. Sigmoid 函数

  • 核心公式：\sigma(x) = \frac{1}{1 + e^{-x}}
  • 输出范围：(0, 1)
  • 特性：
    • 将任意输入映射到 (0,1) 区间，可模拟 “概率”（如二分类任务的输出层）；
    • 缺点：输入绝对值较大时(x \to \pm\infty)，导数趋近于 0，导致梯度消失；输出非零均值（均值约 0.5），会导致后续层输入偏移，影响训练效率。
  • 适用场景：二分类任务的输出层（配合交叉熵损失）。

2. Tanh 函数（双曲正切函数）

  • 核心公式：\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = 2\sigma(2x) - 1
  • 输出范围：(-1, 1)
  • 特性：
    • 是 Sigmoid 的 “零中心化” 版本（输出均值接近 0），解决了 Sigmoid 的输入偏移问题；
    • 缺点：仍存在梯度消失问题(x \to \pm\infty)时导数趋近于 0）。
  • 适用场景：早期 RNN（如 LSTM）的隐藏层，或对输出范围有对称需求的场景。

二、非饱和激活函数（现代主流型）

“非饱和” 指函数在正区间（或部分区间）导数恒定（如 1），从根本上缓解了梯度消失问题，是当前 CNN、Transformer 等模型的首选。

1. ReLU 函数（Rectified Linear Unit，修正线性单元）

  • 核心公式：\text{ReLU}(x) = \max(0, x)
  • 输出范围：[0, +\infty)
  • 特性：
    • 优点：计算极快（仅需判断正负）；x > 0 时导数为 1，完全避免梯度消失；稀疏激活    ( x < 0 时输出为 0，减少神经元冗余）；
    • 缺点：存在死亡 ReLU 问题（若训练中某神经元输入长期为负，其权重会永久冻结，无法更新）。
  • 适用场景：CNN、Transformer 的隐藏层（当前最广泛使用的激活函数）。

2. Leaky ReLU 函数（带泄漏的 ReLU）

  • 核心公式：\text{Leaky ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}
  • 其中 \alpha 是人工设定的小正数（通常取0.01或0.02）。
  • 输出范围：(-\infty, +\infty)
  • 特性：
    • 解决了 “死亡 ReLU 问题”（x < 0时仍有微小梯度 \alpha ，允许权重更新）；
    • 缺点：\alpha 是固定超参数，无法自适应数据分布。
  • 适用场景：替代 ReLU，尤其适用于可能出现大量负输入的网络（如深层 CNN）。

3. ELU 函数（Exponential Linear Unit，指数线性单元）

  • 核心公式：\text{ELU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha (e^x - 1) & \text{if } x \leq 0 \end{cases}
  • 其中 \alpha > 0 是超参数（通常取1.0）。
  • 输出范围：(-\alpha, +\infty)
  • 特性：
    • 兼具 Leaky ReLU 的优点（x < 0 时非零输出，避免死亡神经元）；
    • 输出更接近零均值（x \to -\infty 时输出趋近于 -\alpha ），降低后续层输入偏移；
    • 缺点：计算复杂度高于 ReLU（需计算指数），训练速度略慢。
  • 适用场景：对训练稳定性要求高的深层网络。

4. Swish 函数

  • 核心公式：\text{Swish}(x) = x \cdot \sigma(\beta x)其中 \sigma 是 Sigmoid 函数，\beta 是可学习参数（或固定为 1.0）。
  • 输出范围：(-\infty, +\infty)
  • 特性：
    • 非线性更强（由 Sigmoid 的平滑特性引入），在深层模型（如 ResNet、Transformer）中表现常优于 ReLU；
    • 处处可导（无 ReLU 的 “折点”），梯度传播更平滑；
    • 缺点：计算复杂度高于 ReLU（需计算 Sigmoid）。
  • 适用场景：大型 CNN、Transformer 的隐藏层（Google 提出，在 ImageNet 等任务中验证有效）。

5. GELU 函数（Gaussian Error Linear Unit，高斯误差线性单元）

  • 核心公式：\text{GELU}(x) = x \cdot \Phi(x)其中\Phi(x)是标准正态分布的累积分布函数（CDF），近似计算式为：\text{GELU}(x) \approx 0.5x \left[1 + \tanh\left(\sqrt{\frac{2}{\pi}} (x + 0.044715x^3)\right)\right]
  • 输出范围：(-\infty, +\infty)
  • 特性：
    • 本质是 “概率加权的 ReLU”（将x乘以其大于 0 的概率 \Phi(x) ），更符合生物神经元的随机激活特性；
    • 平滑性优于 ReLU，梯度传播更稳定，在 Transformer 模型中表现极佳；
  • 适用场景：Transformer（如 BERT、GPT）的隐藏层（当前 Transformer 的默认激活函数）。

三、输出层专用激活函数

此类函数需配合特定损失函数，满足任务的输出约束（如概率、多分类、回归）。

1. Softmax 函数（多分类输出）

  • 核心公式（对K分类任务，输入为向量\mathbf{z} = [z_1, z_2, ..., z_K]）：\text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \quad (i=1,2,...,K)
  • 输出范围：每个输出值 \in (0,1)，且所有输出之和为 1（概率分布）。
  • 特性：将多维度输入映射为 “类别概率”，配合交叉熵损失解决多分类问题。

2. Linear 函数（回归任务输出）

  • 核心公式：\text{Linear}(x) = x
  • 输出范围：(-\infty, +\infty)（无约束）。
  • 特性：无非线性，直接输出模型预测值，配合MSE（均方误差） 损失解决回归任务（如房价预测、股价预测）。

http://www.dtcms.com/a/473684.html

相关文章：

  • 回归预测 | MATLAB实现CNN(卷积神经网络)多输入单输出+SHAP可解释分析+新数据预测
  • 中国十大旅游网站wordpress视频试看付费
  • Docker部署的gitlab升级的详细步骤(升级到17.6.1版本)
  • 一个基于稀疏混合专家模型（Sparse Mixture of Experts, Sparse MoE） 的 Transformer 语言模型
  • Litho项目架构解析：四阶段流水线如何实现自动化文档生成
  • 济南建站免费模板logo制作用什么软件
  • Docker为什么比虚拟机资源利用率高，启动快
  • AI 颠覆室内设计：SpatialGen 实现 “一句话生成 3D 房间”
  • 有序逻辑回归的概念、适用场景、数据要求，以及其在Stata中的操作命令及注意事项，Stata ologit回归结果怎么看？并附详细示例
  • PHP开发环境搭建
  • 门户网站与官网的区别做照片的ppt模板下载网站
  • Next.js数据获取演进史
  • 【深入理解计算机网络09】路由算法与路由协议
  • 手机域名解析错误刷seo排名
  • Golang 切片（深入了解切片底层扩容机制，部分源码，测试实战+核心用法）
  • go语言结构体内存对齐
  • 爬虫+卷积神经网络项目实战解析——对图像狗的识别分类
  • golang读写锁
  • 怎么用ftp清空网站大庆seo推广
  • 云南网官方网站博客园和wordpress
  • MyBatis基本工作原理
  • 第16届深圳国际移动电子展AI生活主题将带来哪些新体验？
  • AI智能体赋能战略分析与制订之仿真：“主权AI” —— 是国家安全的“诺亚方舟”，还是创新生态的“孤岛”？
  • 公司手机网站建设wordpress页眉页脚
  • MySQL时间格式转换，时间数据混乱不堪如何彻底重构？
  • Docker 安装 Node.js
  • vscode 怎么运行 c++ 文件
  • 【基础算法】记忆化搜索
  • wordpress yum上海搜索引擎优化公司排名
  • c++类和对象（下）