【基础算法】记忆化搜索

一、记忆化搜索

1. 什么是记忆化搜索

记忆化搜索也是一种剪枝策略。通过创建一个 “备忘录”，记录第一次搜索到的结果，当下一次搜索到这个状态时，直接在 “备忘录” 里面找结果，而不用去重新计算。

记忆化搜索，有时候也叫动态规划。

---

2. 【案例】斐波那契数

【题目链接】

509. 斐波那契数 - 力扣（LeetCode）

这道题十分经典，解决方法也很多。我们很容易写出下面的代码：

class Solution 
{
public:int fib(int n) {if(n == 1 || n == 0) return n;else return fib(n - 1) + fib(n - 2);}
};

但是，这样很容易就超时了，原因在于我们实际上重复计算了很多项。

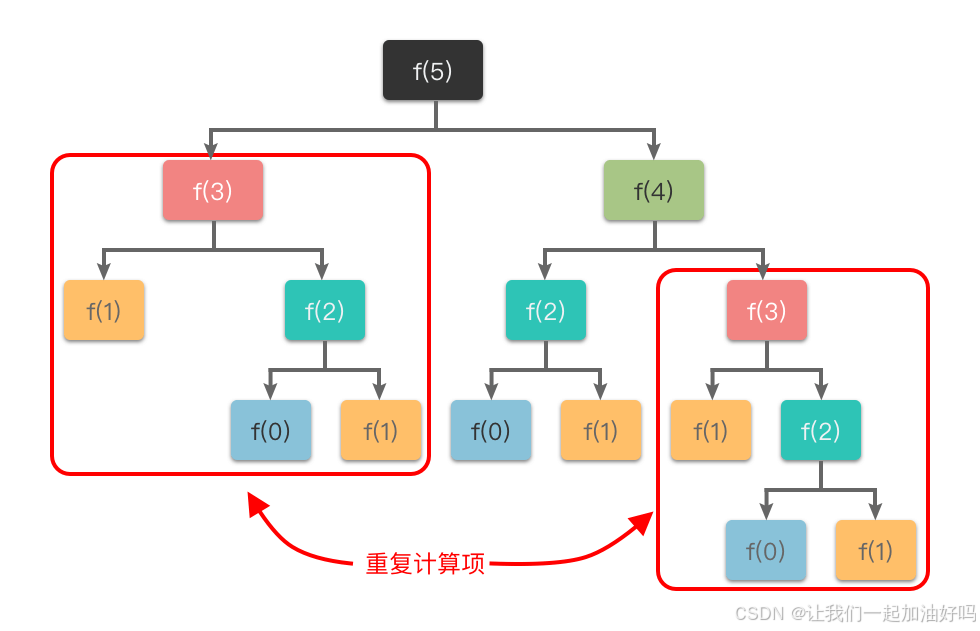
如果不想重复计算，我们可以创建一个数组，下标为 n 的地方用于存储 f(n) 的计算结果，当我们第一次计算某个 f(i) 的时候，计算完成我们就把结果存储在对应的位置，那么当下一次我们再次遇到 f(i) 时就可以直接从里面拿值而非再递归重新计算。这种优化方案就是记忆化搜索。

class Solution 
{int memo[101];
public:int dfs(int n){if(n <= 1) return n;// 如果数组里面的值不是 -1，说明我们已经计算过了，直接拿值返回即可if(memo[n] != -1) return memo[n];// 数组里面的值是 -1, 说明第一次计算，正常递归进去计算memo[n] = dfs(n - 1) + dfs(n - 2);// 计算完之后返回这个值即可return memo[n];}int fib(int n) {// 把数组里的值全部初始化为 -1// 之所以初始化为 -1 而非 0，是因为避免与 f(0) 混淆memset(memo, -1, sizeof(memo));return dfs(n);}
};

---

二、OJ 练习

1. Function ⭐

【题目链接】

P1464 Function - 洛谷

【题目描述】

对于一个递归函数 $w(a,b,c)$

• 如果 $a\le 0$ 或 $b\le 0$ 或 $c\le 0$ 就返回值 $1$。
• 如果 $a>20$ 或 $b>20$ 或 $c>20$ 就返回 $w(20,20,20)$
• 如果 $a<b$ 并且 $b<c$ 就返回 $w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c)$。
• 其它的情况就返回 $w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1)$

这是个简单的递归函数，但实现起来可能会有些问题。当 $a,b,c$ 均为 $15$ 时，调用的次数将非常的多。你要想个办法才行。

注意：例如 $w(30,-1,0)$ 又满足条件 $1$ 又满足条件 $2$，请按照最上面的条件来算，答案为 $1$。

【输入格式】

会有若干行。

并以 $-1,-1,-1$ 结束。

【输出格式】

输出若干行，每一行格式：

w(a, b, c) = ans

注意空格。

【示例一】

1 1 1
2 2 2
-1 -1 -1

【示例二】

w(1, 1, 1) = 2
w(2, 2, 2) = 4

【说明/提示】

保证输入的数在 $[-9223372036854775808,9223372036854775807]$ 之间，并且是整数。

保证不包括 $-1,-1,-1$ 的输入行数 $T$ 满足 $1\le T\le 10^5$。

---

(1) 解题思路

其实这道题就是加强版的斐波那契数，当我们举一个例子画出递归展开图时我们会发现，出现了大量的重复子问题，因此为了避免大量的重复计算，我们需要剪枝，于是可以采用记忆化搜索。

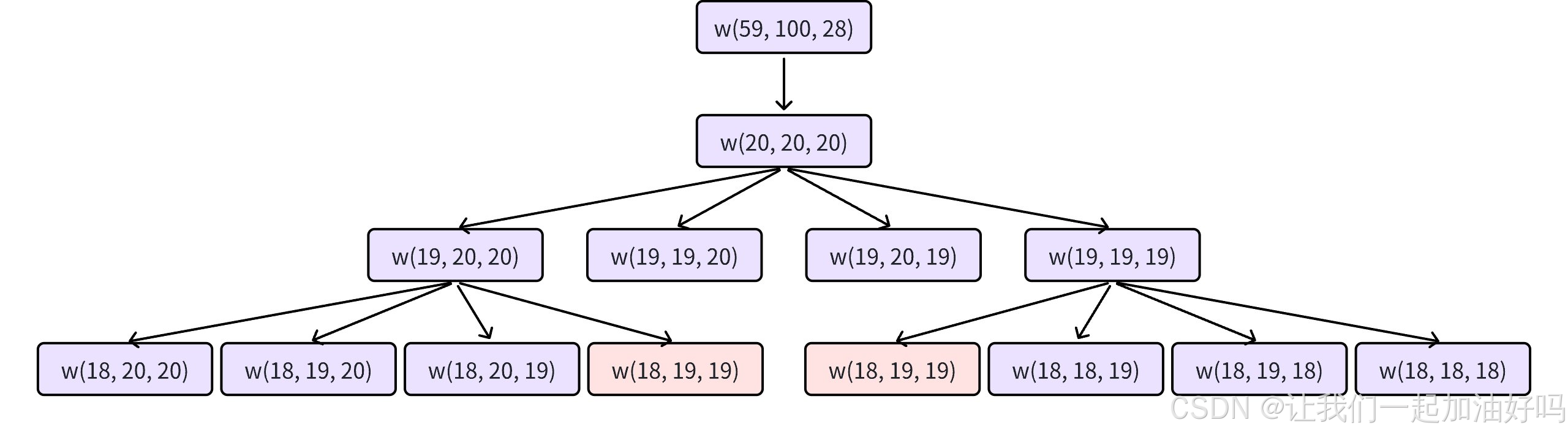
我们依旧创建一个备忘录，当发现是第一次计算的时候，我们正常按照规则进行计算并把对应的值存进备忘录中。当发现备忘录中的值已经计算过了时，我们直接拿值返回即可。

---

(2) 代码实现

#include<iostream>using namespace std;typedef long long LL;
const int N = 25;
int f[N][N][N];  // 备忘录，f[a][b][c] 存储的是 w(a, b, c) 的值LL w(LL a, LL b, LL c)
{if(a <= 0 || b <= 0 || c <= 0) return 1;if(a > 20 || b > 20 || c > 20) return w(20, 20, 20);// 当备忘录中的值非 0，即已经计算过了，直接拿值if(f[a][b][c]) return f[a][b][c];// 下面就是没有计算过的情况// 按照题目中的规则计算然后存入备忘录中即可if(a < b && b < c){f[a][b][c] =  w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);return f[a][b][c];}f[a][b][c] = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b ,c - 1) - w(a - 1, b - 1, c - 1);return f[a][b][c];
}int main()
{while(1){LL a, b, c;cin >> a >> b >> c;if(a == -1 && b == -1 && c == -1) break;printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, w(a, b, c));}return 0;
}

---

2. 天下第一 ⭐⭐

【题目链接】

P5635 【CSGRound1】天下第一 - 洛谷

【题目背景】

天下第一的 cbw 以主席的身份在 8102 年统治全宇宙后，开始了自己休闲的生活，并邀请自己的好友每天都来和他做游戏。由于 cbw 想要显出自己平易近人，所以 zhouwc 虽然是一个蒟蒻，也有能和 cbw 玩游戏的机会。

【题目描述】

游戏是这样的：

给定两个数 $x$，$y$，与一个模数 $p$。

cbw 拥有数 $x$，zhouwc 拥有数 $y$。

第一个回合：$x\leftarrow (x+y)\mathrm{mod}p$。

第二个回合：$y\leftarrow (x+y)\mathrm{mod}p$。

第三个回合：$x\leftarrow (x+y)\mathrm{mod}p$。

第四个回合：$y\leftarrow (x+y)\mathrm{mod}p$。

以此类推…

如果 $x$ 先到 $0$，则 cbw 胜利。如果 $y$ 先到 $0$，则 zhouwc 胜利。如果 $x,y$ 都不能到 $0$，则为平局。

cbw 为了捍卫自己主席的尊严，想要提前知道游戏的结果，并且可以趁机动点手脚，所以他希望你来告诉他结果。

【输入格式】

有多组数据。

第一行：$T$ 和 $p$ 表示一共有 $T$ 组数据且模数都为 $p$。

以下 $T$ 行，每行两个数 $x,y$。

【输出格式】

共 $T$ 行

$1$ 表示 cbw 获胜，$2$ 表示 zhouwc 获胜，error表示平局。

【示例一】

输入

1 10
1 3

输出

error

【示例二】

输入

1 10
4 5

输出

1

【说明/提示】

$1\le T\le 200$。

$1\le x,y,p\le 10000$。

---

(1) 解题思路

我们可以把递归函数 dfs 的返回值设置为 char，返回值为 '1' 表示 cbw 胜，返回值为 '2' 表示 zhouwc 胜，'e' 表示平局。传入参数 x 和 y，那么只要 x 为 0 就返回 ’1‘，只要 y 为 0 就返回 '2'。如果二者都不为 0，那么就递归到下一轮，根据模运算的性质，我们可以直接返回 dfs((x + y) % p, (x + y + y) % p)。

但是这样遇到平局的话就会出现死循环，于是我们需要采用记忆化搜索的方式来发现这一个重复的情况。我们可以创建一个备忘录 char f[N][N]，值为 '1' 表示 cbw 胜，值为 '2' 表示 zhouwc 胜，'e' 表示平局。初始化为空字符，只要走到一个位置，就把对应位置设置为 'e'，如果再次遇到，说明这局必定为平局，那么返回这个 'e' 即可。

---

(2) 代码实现

#include<iostream>using namespace std;const int N = 1e4 + 10;
int x, y, p;// 备忘录f[x][y]记录对应值为 x, y 时的胜负情况
// '1': cbw胜  '2': zhouwc胜  'e': 平局
char f[N][N];
// 用 char 原因是防止爆空间char dfs(int x, int y)
{// 如果备忘录里有值，直接拿值if(f[x][y]) return f[x][y];// 只要第一次计算，就先把它设置成平局，这样再次遇到时，就可以返回 'e' 平局的信息f[x][y] = 'e';// 而如果这时候有一个变成 0 了，就把备忘录中的信息修改正确了再返回if(x == 0) return f[x][y] = '1';if(y == 0) return f[x][y] = '2';// 还没有分出胜负就继续return f[x][y] = dfs((x + y) % p, (x + y + y) % p);
}int main()
{int T;cin >> T >> p;while(T--){cin >> x >> y;char ret = dfs(x, y);if(ret == '1') cout << '1' << endl;if(ret == '2') cout << '2' << endl;if(ret == 'e') cout << "error" << endl;}return 0;
}

---

3. 滑雪 ⭐⭐

【题目描述】

Michael 喜欢滑雪。这并不奇怪，因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子：

1   2   3   4   5
16  17  18  19  6
15  24  25  20  7
14  23  22  21  8
13  12  11  10  9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度会减小。在上面的例子中，一条可行的滑坡为 $24-17-16-1$（从 $24$ 开始，在 $1$ 结束）。当然 $25$－$24$－$23$－$\dots$－$3$－$2$－$1$ 更长。事实上，这是最长的一条。

【输入格式】

输入的第一行为表示区域的二维数组的行数 $R$ 和列数 $C$。下面是 $R$ 行，每行有 $C$ 个数，代表高度（两个数字之间用 $1$ 个空格间隔）。

【输出格式】

输出区域中最长滑坡的长度。

【示例一】

输入

5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9

输出

25

【说明/提示】

对于 $100\%$ 的数据，$1\le R,C\le 100$。

---

(1) 解题思路

暴力枚举，遍历整个矩阵，看看以当前位置为起点，最远能滑行多远的距离。在所有情况里面，取最大值即可。

如何计算从某个位置 [x, y] 开始的最远滑行距离？只需直到我们当前位置的上下左右四个位置（如果存在的话）能滑行的最远距离的最大值然后 + 1 即可。即大致思路为：

dfs(x, y) = max(dfs(x - 1, y), dfs(x + 1, y), dfs(x, y - 1), dfs(x, y + 1)) + 1

当然这其中需要判断有没有上下左右，并且只有高度比当前位置低才能到该位置。更重要的是，我们在计算的过程中，某个位置能滑行的最远距离一定是确定的，当我们计算了一次之后就可以保存下来不必再次递归计算。因此我们可以采用记忆化搜索进行优化。

---

(2) 代码实现

#include<iostream>using namespace std;
const int N = 105;
int h[N][N];  // 记录高度
int f[N][N];  // 备忘录
int r, c;// 从 [x, y] 位置开始能滑行的最远距离
int dfs(int x, int y)
{// 如果计算过了，直接拿值返回即可if(f[x][y]) return f[x][y];int t = 1;  // 记录最远距离，最小为 1// 上if(y > 0 && h[x][y - 1] < h[x][y]) t = max(t, dfs(x, y - 1) + 1);// 下if(y < c - 1 && h[x][y + 1] < h[x][y]) t = max(t, dfs(x, y + 1) + 1);// 左if(x > 0 && h[x - 1][y] < h[x][y]) t = max(t, dfs(x - 1, y) + 1);// 右if(x < r - 1 && h[x + 1][y] < h[x][y]) t = max(t, dfs(x + 1, y) + 1);f[x][y] = t;return f[x][y];
}int main()
{cin >> r >> c;for(int i = 0; i < r; i++)for(int j = 0; j < c; j++)cin >> h[i][j];int res = -1;for(int i = 0; i < r; i++)for(int j = 0; j < c; j++)res = max(res, dfs(i, j));cout << res << endl;return 0;
}