当前位置：首页 > news >正文

Tensorflow循环神经网络RNN

news 2025/10/13 6:37:26

循环神经网络是一种专门用于处理序列数据的人工神经网络。
序列数据：数据点之间存在顺序依赖关系，前一个数据点会影响后一个数据点。例如城市每小时的温度、文本单词的顺序排列、天气数据等。一旦RNN学习了数据中过去的模式，它便能够利用这些知识来预测未来，当然，前提是过去的模式仍然在未来成立。
普通的前馈神经网络在处理一个句子中每个单词的时候，完全不知道前面出现过的单词，将每个单词当作独立的、不相关的输入，无法理解语言上下文的含义。RNN的解决思路是在处理下一个单词的时候会将上一个单词产生的状态和记忆一并作为输入，这样，网络就具备上下文信息。
此外，将探讨RNN面临的两个主要问题：不稳定的梯度，可以通过各种技术（包括循环Dropout和循环层归一化）来缓解；非常有限的短期记忆，可以使用LSTM和GRU单元进行扩展。

一、循环神经元和层

前馈神经网络，其中激活仅在一个方向上流动，从输入层流向输出层。循环神经网络看起来非常像前馈神经网络，只不过它还具有反向的连接。

最简单的RNN：它由一个接收输入、产生输出并将输出或状态反送回自身的神经元组成。在每个时间步长t（也称为帧），该循环神经元接收输入x(t)和前一个时间步长的输出ŷ(t-1)。由于在第一个时间步长中不涉及先前的输出，因此通常将其设置为0。可以沿时间轴来展开这个小网络，如图所示。这被称为时间展开网络（它是同一循环神经元在每个时间步长的表示）。

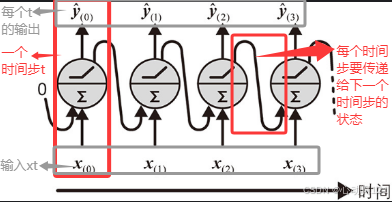
每个循环神经元都有两组权重：一组用于输入x(t)，另一组用于前一个时间步长的输出ŷ(t-1)。我们称这些权重向量为wx和wŷ。如果考虑整个循环神经元层（简称“循环层”）而不仅仅是一个循环神经元，则可以将所有权重向量放在wx和wŷ这两个权重矩阵中。然后，可以如预期的那样计算整个循环层的输出向量，如公式所示，其中b是偏置向量，φ()是激活函数（例如ReLU)

单个实例的循环层输出： $\hat{y}_{(t)} = \phi(W_x^{T}x_{(t)} + W_{\hat{y}}^{T}\hat{y}_{(t-1)} + b)$

就像前馈神经网络一样，可以通过将时间步长处的所有输入放在输入矩阵 $X_{(t)}$ 中，来一次性计算出整个小批量的循环层输出： $\hat{Y}_{(t)} = \phi(X_{(t)}W_x + \hat{Y}_{(t-1)}W_{\hat{y}} + b)$ ，也可以写成： $\hat{Y}_{(t)} = \phi(([X_{(t)} \ \hat{Y}_{(t-1)}]W + b)), \quad W = \begin{bmatrix} W_x \\ W_{\hat{y}} \end{bmatrix}$

在此等式中：

$\hat{Y}_{(t)}$ ：是一个 $m \times n_{\text{neurons}}$ 矩阵，包含小批量中每个实例在时间步长 t 处该层的输出。（m 是小批量中的实例数量， $n_{\text{neurons}}$ 是神经元数量。）该函数是关于 $X_{(t)},\hat{Y}_{(t-1)}$ 的函数。这使 $\hat{Y}_{(t)}$ 成为自时间 t=0 以来所有输入（即 $X_{(0)}, X_{(1)}, \ldots, X_{(t)}$ ）的函数。在第一个时间步长 t=0 时，没有先前的输出，因此通常假定它们均为零。
$X_{(t)}$ ：是一个 $m \times n_{\text{inputs}}$ 矩阵，包含所有实例的输入。（ $n_{\text{inputs}}$ 是输入特征的数量。）
$W_x$ ：是一个 $n_{\text{inputs}} \times n_{\text{neurons}}$ 矩阵，包含当前时间步长的输入连接权重。
$W_{\hat{y}}$ ：是一个 $n_{\text{neurons}} \times n_{\text{neurons}}$ 矩阵，包含前一时间步长的输出连接权重。
$b$ ：是大小为 $n_{\text{neurons}}$ 的向量，包含每个神经元的偏置项。
权重矩阵 $W_x,W_{\hat{y}}$ 经竖直重合并形成形状为 $(n_{\text{inputs}} + n_{\text{neurons}}) \times n_{\text{neurons}}$ 的单个权重矩阵 W
符号 $[X_{(t)} \ \hat{Y}_{(t-1)}]$ 表示矩阵 $X_{(t)},\hat{Y}_{(t-1)}$ 的水平合并。

1、记忆单元（循环神经元）

由于在时间步长t时，循环神经元的输出是先前时间步长中所有输入的函数，因此，可以说他是具有记忆的形式。神经网络中跨时间步长保留某些状态的部分被称为记忆单元。

单个神经元或神经元层是非常基本的单元，只能够学习短模式（通常约为10个步长）。能够学习更长的模式需要更复杂的单元类型（循环神经元），也就是说需要在单个神经元输出 ŷ 的基础之上还有一个关于状态的输出h(t)。

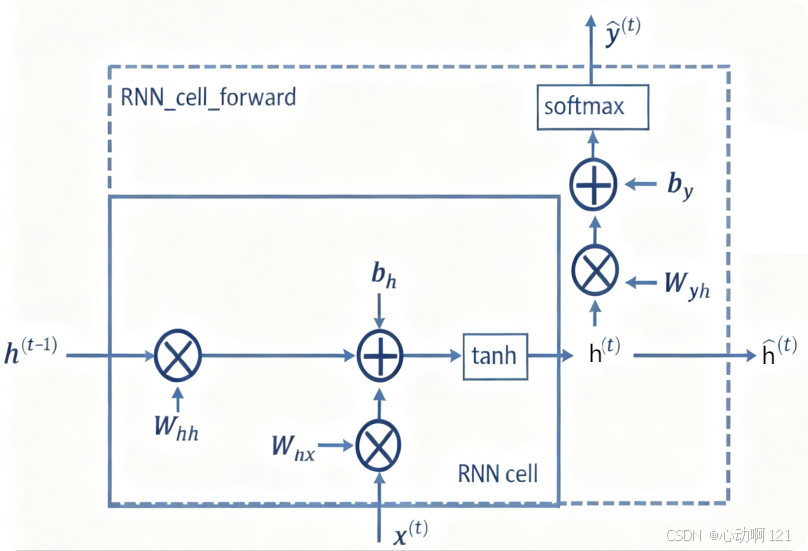
LSTM神经元：比简单的循环神经元复杂的多，内部包含三个门（遗忘门、输入门、输出门）和一个细胞状态（像一条传送带，在整个链上运行，只有少量的线性交互，使得信息可以很容易地保持不变地流过）

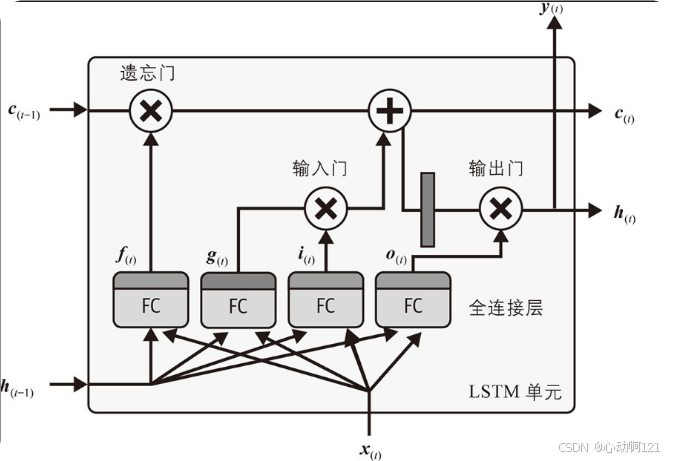
$\begin{aligned} i_{(t)} &= \sigma\left(W_{xi}^{\top} x_{(t)} + W_{hi}^{\top} h_{(t-1)} + b_i \right) \\ f_{(t)} &= \sigma\left(W_{xf}^{\top} x_{(t)} + W_{hf}^{\top} h_{(t-1)} + b_f \right) \\ o_{(t)} &= \sigma\left(W_{xo}^{\top} x_{(t)} + W_{ho}^{\top} h_{(t-1)} + b_o \right) \\ g_{(t)} &= \tanh\left(W_{xg}^{\top} x_{(t)} + W_{hg}^{\top} h_{(t-1)} + b_g \right) \\ c_{(t)} &= f_{(t)} \otimes c_{(t-1)} + i_{(t)} \otimes g_{(t)} \\ h_{(t)} &= o_{(t)} \otimes \tanh\left(c_{(t)}\right) \\ y_{(t)} &= h_{(t)} \end{aligned}$

2、循环层

单个循环神经元的能力有限，为了增强模型的表达能力，会将多个循环神经元并行的组织在一起，形成一个循环层。一个全连接层是多个传统神经元的集合。同样，一个循环层是多个循环神经元的集合。

在循环层中，输入 x_t、隐藏状态 h_t 都从标量变成了向量。x_t 是一个向量，表示在时间步 t 的所有输入特征。h_t 是一个向量，它的维度等于该层中循环神经元的数量（也称为隐藏单元数）。这个向量的每一个元素，都对应一个循环神经元的当前状态。

循环层在处理一个序列的时候有两种输出模式：一个是返回最后一个隐藏状态（ return_sequences = False ）适用于多对一的任务；另一个是返回整个状态序列（ return_sequences = True ）适用于多对多的任务。

由于数据在遍历RNN时会经历转换，因此在每个时间步都会丢失一些信息。一段时间后，RNN的状态几乎不包含第一个输入的踪迹。为了解决这个问题，人们引入了具有长期记忆的各种类型的单元。其中最受欢迎的是LSTM单元。

由多个基本的LSTM神经元组成LSTM层，GRU层。GRU层是LSTM的一个简化版，它将遗忘门和输入门合并为一个“更新门”，并混合了细胞状态和隐藏状态。它参数更少，计算更快，但在多数任务上表现与LSTM相当。

model = tf.keras.Sequential([tf.keras.layers.LSTM(32, return_sequences=True, input_shape=[None, 5]),tf.keras.layers.Dense(14)
])
opt = tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9)
early_stopping_cb = tf.keras.callbacks.EarlyStopping(monitor="val_mae", patience=50, restore_best_weights=True)
model.compile(loss=tf.keras.losses.Huber(), optimizer=opt, metrics=["mae"])
history = model.fit(seq2seq_train, validation_data=seq2seq_valid, epochs=500, callbacks=[early_stopping_cb])

利用循环层具有状态性和序列处理能力这一核心特性，来构建出功能强大的模型，解决从图像描述到机器翻译等各种复杂的序列问题。

概念	描述	与循环层的关系
向量到序列	从一个固定向量生成一个变长序列。	循环层作为解码器，利用其循环性（隐藏状态）来逐步生成有序序列。
序列到向量	将一个变长序列编码为一个固定向量。	循环层作为编码器，通过处理整个序列并将其最终状态作为总结。
编码器-解码器	一个两阶段模型，先将序列编码为向量，再将该向量解码为另一个序列。	核心由两个循环层网络构成：一个作为编码器，一个作为解码器。它完美结合了前两种模式，是处理序列转换任务（如翻译）的基石。

向量到序列的网络：在每个时间步长中一次又一次地向网络提供相同的输入向量，并让其输出一个序列，这是多对多或编码器-解码器的简化版。

序列到向量的网络：读取并理解整个输入序列（如一句英文句子），之后将整个序列的语义压缩成一个单一的固定长度的向量。

最后，可能有一个称为编码器的序列到向量的网络，后跟一个称为解码器的向量到序列的网络。例如，这可以用于将句子从一种语言翻译成另一种语言。可以用一种语言向网络输入一个句子，编码器会将其转换为单个向量表示，然后解码器会将此向量解码为另一种语言的句子。这种称为“编码器—解码器”(Encoder-Decoder)的两步模型比使用单个序列到序列的RNN进行即时翻译要好得多：句子的最后一个单词会影响翻译的第一个单词，因此在翻译之前需要等待，直到看完整个句子。

二、RNN预测时间序列

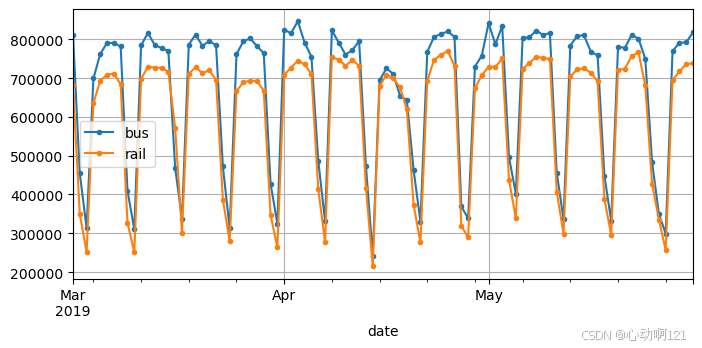
如图所示的数据具备每周季节性(seasonality)，这样的模式很强大，以至于仅通过复制一周前的值来预测明天的乘客量便可产生相当不错的结果。这称为朴素预测：通过简单地复制过去的值来做出预测。朴素预测通常是一个很好的基准，在某些情况下甚至很难被击败。

为了可视化这些朴素预测，我们用虚线叠加两个时间序列（bus和rail）以及滞后一周（即向右移动）的相同时间序列。还将绘制两者之间的差异（即时间t处的值减去时间t-7处的值），这称为差分

现在我们有个基准（即朴素预测), 尝试使用到目前为止介绍的机器学习模型来预测这个时间序列，先从一个基本的线性模型开始。目标是根据过去8周（56天）的客运量数据来预测“明天”的客运量。因此，模型的输入将是序列（一旦模型投入生产，通常每天一个序列），每个序列包含从时间步t-55到t的56个值。对于每个输入序列，模型将输出一个值：时间步t+1的预测值。

1、准备数据

如何准备训练数据：将使用过去的每个56天（作为窗口）作为训练数据，每个窗口对应的目标值将是紧随其后的值。Keras实际上有一个很好的实用函数（叫作tf.keras.utils.timeseries_dataset_from_array()），它可以帮助准备训练集。它以时间序列作为输入，并构建一个包含所需长度的所有窗口及其相应目标值的tf.data.Dataset。获得相同结果的另一种方法是使用tf.data的Dataset类的window()方法。它更复杂，但它给了完全的控制权，window()方法返回窗口数据集的数据集。

# 方法一
import tensorflow as tf
my_series = [0,1,2,3,4,5]
my_dataset = tf.keras.utils.timeseries_dataset_from_array(my_series,targets=my_series[3:],sequence_length=3,batch_size=2
)# 方法二： 创建辅助函数，更方便地从数据集提取窗口
def to_windows(dataset, length):dataset = dataset.window(length, shift=1, drop_remainder=True)return dataset.flat_map(lambda window_ds: window_ds.batch(length))
# 使用map方法将每个窗口拆分为输入和目标值，然后将生成的窗口分组为大小为2的批次
dataset = to_windows(tf.data.Dataset.range(6), 4)
dataset = dataset.map(lambda window: (window[:-1], window[-1]))
list(dataset.batch(2))

接下来，使用timeseries_dataset_from_array()创建用于训练和验证的数据集。由于梯度下降期望训练集中的实例独立同分布(IID)，因此必须设置参数shuffle=True来打乱训练窗口

import pandas as pd
from pathlib import Pathpath = Path("datasets/ridership/CTA_-_Ridership_-_Daily_Boarding_Totals.csv")
df = pd.read_csv(path, parse_dates=["service_date"])
df.columns = ["date", "day_type", "bus", "rail", "total"]  #  更短的名字
df = df.sort_values("date").set_index("date")
df = df.drop("total", axis=1)  # 不需要全部，只需要bus + rail
df = df.drop_duplicates()  # 删掉重复的月份 (2011-10 and 2014-07)# 拆分训练，验证和测试，并归一化
rail_train = df["rail"]["2016-01":"2018-12"] / 1e6
rail_valid = df["rail"]["2019-01":"2019-05"] / 1e6
rail_test = df["rail"]["2019-06":] / 1e6
seq_length = 56
train_ds = tf.keras.utils.timeseries_dataset_from_array(rail_train.to_numpy(),targets=rail_train[seq_length:],sequence_length=seq_length,batch_size=32,shuffle=True,seed=42
)
valid_ds = tf.keras.utils.timeseries_dataset_from_array(rail_valid.to_numpy(),targets=rail_valid[seq_length:],sequence_length=seq_length,batch_size=32,
)

2、使用不同的模型进行预测

（1）使用线性模型进行预测

tf.random.set_seed(42)model = tf.keras.Sequential([tf.keras.layers.Dense(1, input_shape=[seq_length])
])
early_stopping_cb = tf.keras.callbacks.EarlyStopping(monitor="val_mae", patience=50, restore_best_weights=True) # monitor 早停的监控指标 val_mae 验证集的平均绝对值误差
opt = tf.keras.optimizers.SGD(learning_rate=0.02, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(), optimizer=opt, metrics=["mae"])
history = model.fit(train_ds, validation_data=valid_ds, epochs=500, callbacks=[early_stopping_cb])
model.evaluate(valid_ds) # 为什么这里是0.03...之前是 42143.271739，因为数据除以了1e6
model.evaluate(valid_ds)[-1] * 1e6 # 这里的结果是37928.10067534447

（2）使用简单的RNN进行预测

Keras中的所有循环层都期望形状为［批量大小、时间步、维度］的三维输入，其中一元时间序列的维度为1，多元时间序列的维度更高。回想一下，input_shape参数忽略了第一个维度（即批量大小），并且由于循环层可以接受任何长度的输入序列，因此可以将第二个维度设置为None，这意味着“任何大小”。最后，由于我们处理的是一元时间序列，因此最后一个维度的大小应为1。这就是我们指定输入形状[None，1]的原因：它表示“任意长度的一元序列”。请注意，数据集实际上包含形状为［批量大小，时间步］的输入，因此缺少最后一个维度（大小为1），但在这种情况下Keras非常友好地为我们添加了它。

model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(1, input_shape=[None, 1])
])
def fit_and_evaluate(model,learning_rate=0.02,epochs=500,train_ds = train_ds, valid_ds = valid_ds):early_stopping_cb = tf.keras.callbacks.EarlyStopping(monitor="val_mae",patience=50, restore_best_weights=True)opt = tf.keras.optimizers.SGD(learning_rate=learning_rate, momentum=0.9)model.compile(loss= tf.keras.losses.Huber(), optimizer=opt, metrics=["mae"])my_history = model.fit(train_ds, validation_data=valid_ds, epochs=epochs, callbacks=[early_stopping_cb])print("验证集误差："+str(model.evaluate(valid_ds)[-1] *1e6))
fit_and_evaluate(model) # 这里的结果是102777.6449918747

它的验证MAE大于100000！这是意料之中的，原因有二：

该模型只有一个循环神经元，因此它在每个时间步可以用来进行预测的唯一数据是当前时间步的输入值和前一个时间步的输出值。换句话说，RNN的记忆极其有限：它只记忆一个数字，即它之前的输出。让我们数一数这个模型有多少个参数：因为该循环神经元只有2个输入值，所以整个模型只有3个参数（2个权重加上1个偏置项）。对于这个时间序列来说，这还远远不够。相比之下，我们之前的模型可以一次查看56个先前的值，它总共有57个参数。
时间序列包含从0到大约1.4的值，但由于默认激活函数是tanh，因此循环层只能输出-1到+1之间的值。它无法预测1.0到1.4之间的值。

让我们来解决这两个问题：我们将创建一个具有更大循环层（包含32个循环神经元）的模型，并在其顶部添加一个密集输出层（具有一个输出神经元且没有激活函数）。循环层能够将更多信息从一个时间步携带到下一个时间步，密集输出层将最终输出从32维投影到一维，没有任何值范围限制：

model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(32,input_shape=[None, 1]),tf.keras.layers.Dense(1)
])
fit_and_evaluate(model) # 这里的结果是30570.054426789284

显然，这个是相对前两个来说是较好的结果。

（3）使用深度RNN进行预测

使用Keras实现深度RNN非常简单：只需堆叠循环层即可。在下面的示例中，使用3个SimpleRNN层,前两个是序列到序列的层，最后一个是序列到向量的层。最后，Dense层（可以将其视为向量到向量的层）生成模型的预测值。所以，这个模型就像图中表示的模型一样，只不过输出Ŷ(0)到Ŷ(t-1)被忽略，并且在Ŷ(t)之上有一个密集层。

deep_model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(32, return_sequences=True, input_shape=[None, 1]),tf.keras.layers.SimpleRNN(32, return_sequences=True),tf.keras.layers.SimpleRNN(32),tf.keras.layers.Dense(1)
])
fit_and_evaluate(deep_model)    # 结果为28308.261185884476

确保为所有循环层设置return_sequences=True（最后一层除外）。如果你忘记为某个循环层设置此参数，它将输出一个仅包含最后一个时间步的输出的二维数组，而不是包含所有时间步的输出的三维数组。下一个循环层会报错：没有以预期的三维格式为其提供序列。。

（4）多元时间序列预测

神经网络的一大优点是它们非常灵活，特别是，它们可以处理多元时间序列而几乎无须改变它们的架构。例如，尝试使用公共汽车和铁路数据作为输入来预测铁路时间序列。事实上，还可以加入日期类型，由于可以提前知道明天是工作日、周末还是假期，因们可以将日期类型序列偏移一天，这样模型就可以将“明天”的日期类型作为输入了。为了简单起见，将使用Pandas进行此处理：

df_mulvar = df[["bus", "rail"]] / 1e6
df_mulvar["next_day_type"] = df["day_type"].shift(-1) # 给数据表加一列，明天是什么日子
df_mulvar = pd.get_dummies(df_mulvar, dtype=float)# 自动将字符串的列转换成独热编码

现在df_mulvar是一个包含5列的DataFrame，这5列分别是公共汽车数据列、铁路数据列，以及包含第二天类型的独热编码的3列（有3种可能的日期类型W、A和U）。接下来可以重复之前的操作。首先，将数据分成训练、验证和测试：

mulvar_train = df_mulvar["2016-01":"2018-12"]
mulvar_valid = df_mulvar["2019-01":"2019-05"]
mulvar_test = df_mulvar["2019-06":]
tf.random.set_seed(42)
train_mulvar_ds = tf.keras.utils.timeseries_dataset_from_array(mulvar_train.to_numpy(),  # 使用5列作为输入，将表格转换成numpytargets=mulvar_train["rail"][seq_length:],  # 只预测铁路序列sequence_length=seq_length,batch_size=32,shuffle=True,seed=42
)
valid_mulvar_ds = tf.keras.utils.timeseries_dataset_from_array(mulvar_valid.to_numpy(),targets=mulvar_valid["rail"][seq_length:],sequence_length=seq_length,batch_size=32
)
mulvar_model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(32, input_shape=[None, 5]),tf.keras.layers.Dense(1)
])
fit_and_evaluate(mulvar_model,train_ds=train_mulvar_ds, valid_ds=valid_mulvar_ds)

它与univar_model RNN的唯一区别是输入形状不同：在每个时间步，该模型接收5个输入而不是1个。该模型实际的验证MAE达到了23000左右。取得了很大的进步！

让RNN同时预测公共汽车和铁路客运量并不难，只需要在创建数据集时更改目标，针对训练集将它们设置为mulvar_train[["bus"，"rail"]][seq_length：]，针对验证集设置为mulvar_valid[["bus"，"rail"]][seq_length：]。还必须在输出Dense层中添加一个额外的神经元，因为它现在必须进行两项预测：一项针对明天的公共汽车客运量，另一项针对铁路客运量。

对多个相关任务使用单个模型可能会比对每个任务使用单独的模型产生更好的性能，不仅因为针对一个任务学习的特征可能对其他任务也有用，而且还因为必须跨多个任务表现良好可以防止模型过拟合

tf.random.set_seed(42)seq_length = 56
train_multask_ds = tf.keras.utils.timeseries_dataset_from_array(mulvar_train.to_numpy(),targets=mulvar_train[["bus", "rail"]][seq_length:],  # 2个目标sequence_length=seq_length,batch_size=32,shuffle=True,seed=42
)
valid_multask_ds = tf.keras.utils.timeseries_dataset_from_array(mulvar_valid.to_numpy(),targets=mulvar_valid[["bus", "rail"]][seq_length:],sequence_length=seq_length,batch_size=32
)tf.random.set_seed(42)
multask_model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(32, input_shape=[None, 5]),tf.keras.layers.Dense(2)
])opt = tf.keras.optimizers.SGD(learning_rate=0.02, momentum=0.9)
multask_model.compile(loss=tf.keras.losses.Huber(), optimizer=opt, metrics=["mae"])
history = multask_model.fit(train_multask_ds, validation_data=valid_multask_ds, epochs=500, callbacks=[early_stopping_cb])# 评估多任务RNN的预测
Y_preds_valid = multask_model.predict(valid_multask_ds)
for idx, name in enumerate(["bus", "rail"]):mae = 1e6 * tf.keras.metrics.MeanAbsoluteError()(mulvar_valid[name][seq_length:], Y_preds_valid[:, idx])print(name, int(mae))

（5）预测未来多个时间步

到目前为止，只预测了下一个时间步的值，但通过适当地改变目标我们可以预测未来多个时间步的值。训练RNN一次性预测未来的14个值。仍然可以使用序列到向量的模型，但它会输出14个值而不是1个值。

但是，首先需要将目标更改为包含接下来的14个值的向量。为此，可以再次使用timeseries_dataset_from_array()，但这次要求它创建没有目标(targets=None)且更长的序列的数据集，长度为seq_length+14。然后，可以使用数据集的map()方法将自定义函数应用于每批序列，将它们拆分为输入和目标值。

def split_inputs_and_targets(mulvar_series, ahead=14, target_col=1):# (32，70，5)return mulvar_series[:, :-ahead], mulvar_series[:, -ahead:, target_col]ahead_train_ds = tf.keras.utils.timeseries_dataset_from_array(mulvar_train.to_numpy(),targets=None,sequence_length=seq_length+14,batch_size=32,shuffle=True,seed=42
).map(split_inputs_and_targets)ahead_valid_ds = tf.keras.utils.timeseries_dataset_from_array(mulvar_valid.to_numpy(),targets=None,sequence_length=seq_length+14,batch_size=32).map(split_inputs_and_targets)
# 输出用14个单元
ahead_model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(32, input_shape=[None, 5]),tf.keras.layers.Dense(14)
])
fit_and_evaluate(ahead_model,train_ds=ahead_train_ds, valid_ds=ahead_valid_ds)
# 训练好后 一次预测接下来的14个值
import numpy as np
X = mulvar_valid.to_numpy()[np.newaxis, :seq_length]  # shape [1, 56, 5]
Y_pred = ahead_model.predict(X)  # shape [1, 14]

（6）使用序列到序列模型进行预测

与其训练模型仅在最后一个时间步预测接下来的14个值，不如训练它在每个时间步预测接下来的14个值。换句话说，可以将这个序列到向量的循环神经网络转变为序列到序列的循环神经网络。这种技术的优点是损失将包含RNN在每个时间步的输出的损失项，而不仅仅包含最后一个时间步的输出的损失项。这意味着将有更多的误差梯度流过模型，并且它们不必在时间中流动那么多，因为它们来自每个时间步的输出，而不仅仅是来自最后一个时间步。这既能稳定训练，又能加速训练。

需要明确的是，在时间步0，模型将输出一个向量，其中包含时间步1到14的预测值。在时间步1，模型将预测时间步2到15的值，以此类推。换句话说，目标是连续窗口的序列，在每个时间步移动一个时间步。目标不再是向量，而是与输入长度相同的序列，每一步都包含一个14维向量。

# 创建辅助函数为序列到序列模型准备数据集。
def to_seq2seq_dataset(series, seq_length=56, ahead=14, target_col=1, batch_size=32, shuffle=False, seed=None):ds = to_windows(tf.data.Dataset.from_tensor_slices(series), ahead+1)ds = to_windows(ds, seq_length).map(lambda S: (S[:, 0], S[:, 1:, target_col])) # 这个维度需要验证下if shuffle:ds = ds.shuffle(8 * batch_size, seed=seed)return ds.batch(batch_size)
# 创建数据集
seq2seq_train = to_seq2seq_dataset(mulvar_train, shuffle=True, seed=42)
seq2seq_valid = to_seq2seq_dataset(mulvar_valid)# 构建序列模型
seq2seq_model = tf.keras.Sequential([tf.keras.layers.SimpleRNN(32, return_sequences=True, input_shape=[None, 5]),tf.keras.layers.Dense(14)
])
fit_and_evaluate(seq2seq_model,0.1,seq2seq_train,seq2seq_valid)import numpy as np
X = mulvar_valid.to_numpy()[np.newaxis, :seq_length]
y_pred_14 = seq2seq_model.predict(X)[0,-1] # 只需要最后一个时间步的输出
Y_pred_valid = seq2seq_model.predict(seq2seq_valid)
for ahead in range(14):preds = pd.Series(Y_pred_valid[:-1, -1, ahead],index=mulvar_valid.index[56 + ahead : -14 + ahead]) # 因为最后几个窗口没有完整 14 步预测（靠近结尾的数据不足），所以这里裁掉最后 14 步，保证索引与预测数组 Y_pred_valid[:-1] 长度匹配。mae = (preds - mulvar_valid["rail"]).abs().mean() * 1e6print(f"MAE for +{ahead + 1}: {mae:,.0f}")

使用RNN（尤其是LSTM/GRU）预测时间序列是一个强大而灵活的方法。其核心流程可以概括为：数据归一化 -> 构建滑动窗口数据集 -> 构建LSTM/GRU模型 -> 训练 -> 预测 -> 反归一化。

查看全文

http://www.dtcms.com/a/473569.html