【论文阅读】Segment Any 3D Gaussians

Abstract

本文提出了一种基于3DGS的高效3D可提示分割方法SAGA。该方法以二维视觉提示作为输入，能够在4毫秒内分割出由三维高斯函数表示的相应三维目标。该方法通过为每个三维高斯函数附加一个尺度门控的亲和性特征，赋予其新的多粒度分割特性来实现。具体而言，针对尺度门控亲和性特征学习，提出了一种尺度感知的对比训练策略。该策略
（1）将SAM模型从二维mask中提取的分割能力提取到亲和性特征中，
（2）采用一种软尺度门控机制，通过根据指定的三维物理尺度调整每个特征通道的幅度，解决3D分割中的多粒度模糊性问题。
评估表明SAGA实现了实时多粒度分割，其质量和SOTA相当。

Introduction

本文提出SAGA，一种将SAM的分割能力无缝整合到3DGS的三维可提示分割方法。SAGA将2D视觉提示作为输入，并输出由3D高斯表示的对应三维目标。
为了实现这一目标，SAGA 面临两个主要挑战。首先，SAGA 需要找到一种有效的方法赋予每个三维高斯函数三维分割的能力，从而保留 3D-GS 的高效率。其次，作为一种鲁棒的可快速分割方法，SAGA 必须有效地解决多粒度模糊性问题，即单个三维高斯函数可能属于不同粒度级别的不同部位或物体。

为了解决这两大挑战，SAGA 分别引入了两种解决方案。首先，SAGA 在场景中的每个三维高斯上附加一个亲和特征，使其具备用于分割的新属性。两个亲和特征之间的相似性指示相应的三个维高斯是否属于同一个三维目标。

其次，受到 GARField（Kim 等，2024）的启发，SAGA 采用一个软尺度门控机制来处理多粒度歧义。根据指定的三维物理尺度，尺度门控调整每个特征通道的幅度。该机制将高斯亲和特征映射到用于不同尺度的各自子空间，从而保留多粒度信息，同时缓解由多粒度歧义带来的特征学习干扰。

为实现这两种解决方案，SAGA 提出了一种尺度感知对比学习策略，该策略将 SAM 的分割能力从二维掩模中提炼到尺度门控亲和特征中。这一策略基于三维尺度来确定图像中像素对之间的相关性。然后利用这些相关性通过一个对应蒸馏损失对渲染的亲和特征进行监督。相关信息通过可微分光栅化算法在反向传播过程中传递给高斯亲和特征。训练完成后，SAGA 实现了实时的多粒度分割，且精确度高。

Related Work

2D可提示分割

2D可提示分割任务在SAM一文中提出，目标是在图像中给定输入提示来指定分割目标时，返回分割掩膜。Segment Anything Model(SAM)是一种开创性的分割基础模型。类似的还有SEEM。在这些模型之前，和可提示二维分割最相关的任务是交互式图像分割。受到SAM的启发，许多研究提出将SAM用于三维分割。本文不同之处在于将重点放在通过3DGS提升SAM的三维能力。

3D辐射场中的分割

随着辐射场的成功，越来越多的研究在其中进行3D分割。

和SAGA最密切相关的方法是GARField，它利用了3D物理尺度来解决3D分割中的多粒度模糊性问题，启发了SAGA的尺度门控机制。然而GARField依赖于隐式特征场来输出3D特征，这需要在不同尺度上重复查询分割，从而降低了效率。相比之下，SAGA的尺度门控机制通过直接和3DGS集成而无需额外计算来提高效率。

Method

首先回顾3DGS和尺度条件3D特征。然后介绍SAGA整体流程，解释尺度门控高斯亲和力特征和尺度感知对比学习。

3.1 Scale-condtioned 3D Feature:

LERF首次提出了一个尺度条件特征场的概念。用于从通过CLIP获得的全局图像嵌入中进行学习。
GARField随后将其引入到体积辐射场分割领域，旨在解决多粒度的歧义性。为了计算二维mask $M$的三维尺度，将M投影到带有相机内参和由预训练辐射场预测的深度信息的三维信息。设P表示得到的点云，$X(P)$ $Y(P)$ $Z(P)$表示$P$的三维坐标分量集合，则mask尺度$S_M$为：
$$S_M=2\sqrt{std(X(P){)}^2+std(Y(P){)}^2+std(Z(P){)}^2}$$
其中std表示一组标量的标准差，由于这些尺度是在三维空间中计算的，因此在不同视图之间通常是一致的。SAGA使用三维尺度进行多粒度分割，但以更高效的方式实现。

3.2 整体流程

如图，给定一个预训练的三维高斯模型$G$，SAGA为G中的每一个三维高斯附加一个高斯亲和特征$f_g\in R^D$。D表示特征维度。
为了处理三维可提示分割固有的多粒度歧义性，SAGA采用软尺度门控机制，将这些特征投影到用于不同尺度s的不同尺度门控特征子空间。

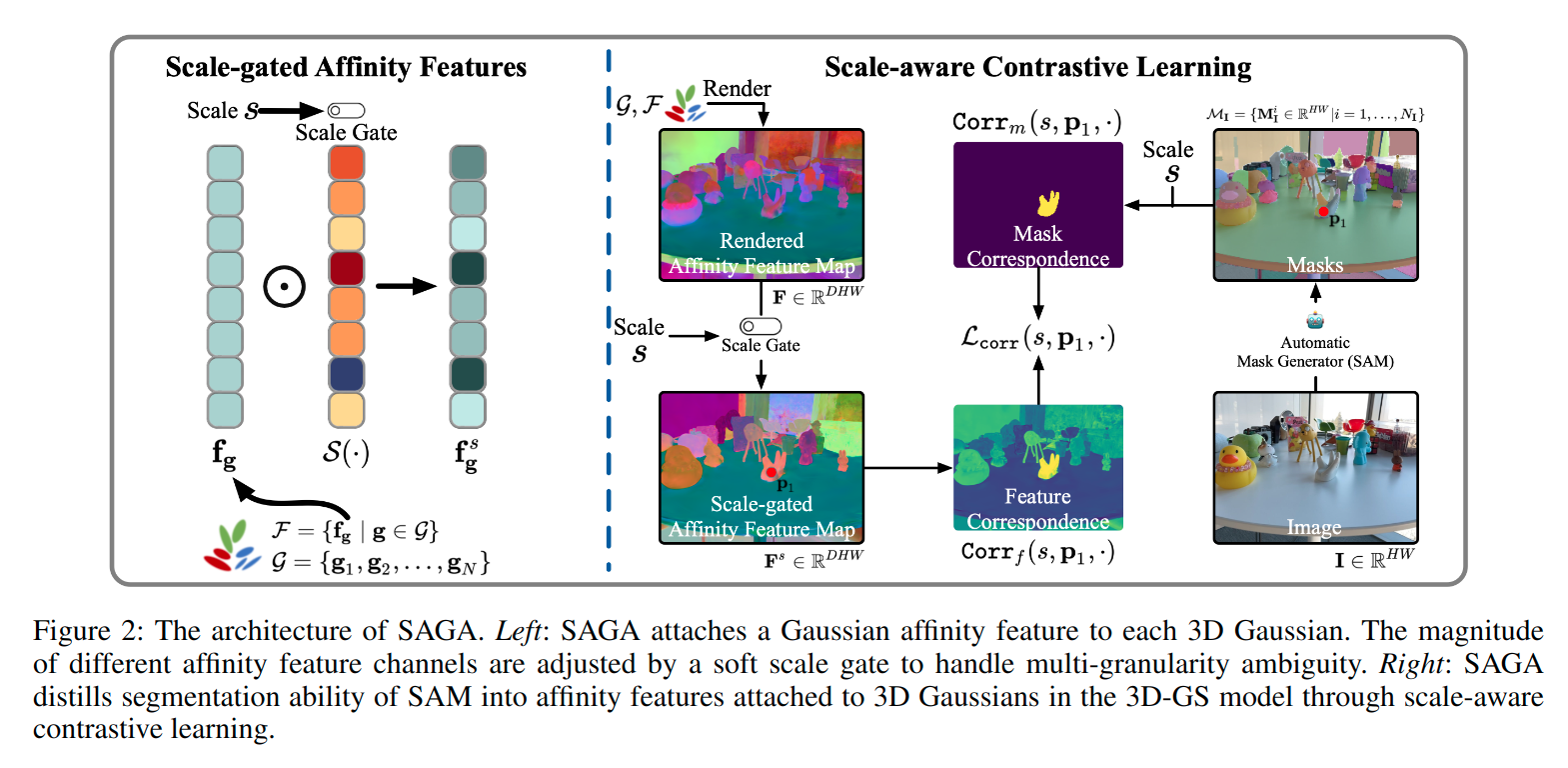
为了训练亲和特征，SAGA从训练集的每一张图像 $I$ 中提取一组多粒度掩膜：
MI={MIi∈{0,1}HW∣i=1,…,NI} \mathcal{M}_{\mathbf{I}}=\left\{\mathbf{M}_{\mathbf{I}}^i \in\{0,1\}^{H W} \mid i=1, \ldots, N_{\mathbf{I}}\right\} MI​={MIi​∈{0,1}HW∣i=1,…,NI​}
其中H,W是图像的高度和宽度。N是提取的mask数量。对于每个mask ${\mathbf{M}}_{\mathbf{I}}^I$，其三维物理尺度 $s_{{\mathbf{M}}_{\mathbf{I}}^i}$ 通过高斯给出的深度和相机位姿计算。
然后，SAGA采用一个尺度感知对比学习策略将多视角2D mask中包含的多粒度分割能力提炼到尺度门控的亲和特征中。在训练完成后，在给定尺度下，两个高斯之间的亲和特征相似性指示它们是否属于同一个3D目标。

推理阶段，给定特定视点，将3D视觉提示（具有尺度的点）转换成相应的三维尺度门控查询特征，并通过评估和3D亲和特征的特征相似性来对3D目标进行分割，此外，凭借训练良好的亲和特征，通过简单聚类即可实现3D场景分解。此外通过和CLIP的结合，SAGA可以在不需要语言字段的情况下执行开放词汇分割。

3.3 高斯亲和特征（Gaussian Affinity Feature）

SAGA的核心是高斯亲和特征： F={fg∣g∈G}F=\{\mathbf{f}_\mathbf{g} | \mathbf{g}\in \mathcal{G}\}F={fg​∣g∈G}
通过用SAM提取的多视角二维掩膜中学习得到。
为了解决提示式分割中固有的多粒度歧义性，引入一个尺度门控机制，将特征空间划分为同于不同三维物理尺度的多个子空间。随后，一个三维高斯在不同粒度下可以属于不同的分割目标而不会产生冲突。

尺度门控亲和特征 （Scale-Gated Affinity Features）

给定一个高斯亲和特征 ${\mathbf{f}}_{\mathbf{g}}$ 和一个特定尺度 $s$，SAGA采用尺度门控来相应地调整各通道的幅值。尺度门控被定义为一个映射：
$$\mathcal{S}:[0,1]\to [0,1{]}^D$$
它将尺度标量 $s\in [0,1]$投影到其对应的软门向量$\mathcal{S}(s)$。为了最大化分割效率，尺度门控设计极其简化：只有一个线性层，加一个sigmoid。
在尺度$s$下，尺度门控的亲和特征为：
$${\mathbf{f}}_{\mathbf{g}}^s=\mathcal{S}(s)\odot {\mathbf{f}}_{\mathbf{g}}$$
其中 $\odot$ 代表逐元素相乘。

因为在尺度s上所有高斯亲和特征共用一个尺度门控，在训练时可以先将亲和特征渲染到二维然后再对二维渲染的特征应用尺度门控：

$$\begin{array}{c}\mathbf{F}(\mathbf{p})=\sum _{i=1}^{|{\mathcal{G}}_{\mathbf{p}}|}{\mathbf{f}}_{{\mathbf{g}}_i^{\mathbf{p}}}{\alpha }_{{\mathbf{g}}_i^{\mathbf{p}}}\prod _{j=1}^{i-1}\left(1-{\alpha }_{{\mathbf{g}}_j^{\mathbf{p}}}\right),\\ {\mathbf{F}}^s(\mathbf{p})=\mathcal{S}(s)\odot \mathbf{F}(\mathbf{p}).\end{array}$$
推理过程中，尺度门控直接应用于高斯亲和特征，以进行三维分割。

局部特征平滑（Local Feature Smoothing）

在实际应用中发现三维空间中存在许多噪声高斯，和分割目标之间的特征相似性很高。这种情况可能由多种原因引起，例如光栅化时权重过小导致训练不足，或3DGS学习到的几何结构不正确。为了解决该问题，SAGA采用了三维高斯的空间局部性先验。在训练过程中使用高斯$\mathbf{g}$的平滑亲和特征来替代原始特征：

$${\mathbf{f}}_{\mathbf{g}}\leftarrow \frac{1}{K}\sum _{{\mathbf{g}}^{\prime }\in \text{KNN}(\mathbf{g})}{\mathbf{f}}_{{\mathbf{g}}^{\prime }}$$

$\text{KNN}(\mathbf{g})$表示g的K个最近邻。训练完成后，每个三维高斯的亲和特征被保存为其平滑后的特征。

3.4 尺度感知对比学习（Scale-Aware Contrastive Learning）

为了训练高斯亲和特征，采用尺度感知对比学习策略，通过可微分光栅化将来自2D掩膜的像素级相关信息蒸馏到三维高斯中。

尺度感知像素身份向量（Scale-aware Pixel Identity Vector）

为了进行尺度感知对比训练，对于图像 $\mathbf{I}$，先将自动提取的2D masks转换成尺度感知的监督信号。为此，给 $\mathbf{I}$ 的每个像素 $P$ 制定一个尺度感知的像素身份向量:
V(s,p)∈{0,1}NI\mathbf{V}(s,\mathbf{p})\in \{0,1\}^{N_\mathbf{I}}V(s,p)∈{0,1}NI​

身份向量反映了像素在特定尺度下所属的2D mask。如果在给定尺度下，两个像素p1、p2共享至少一个相同mask（$\mathbf{V}(s,{\mathbf{p}}_1)\cdot \mathbf{V}(s,{\mathbf{p}}_2)>0$），那它们在尺度 $s$ 下应具有相似的特征。

计算像素身份向量的步骤是：首先按照mask尺度对集合 ${\mathcal{M}}_{\mathbf{I}}$ 进行降序排序，得到有序的mask列表:
$${\mathcal{O}}_{\mathbf{I}}=({\mathcal{M}}_{\mathbf{I}}^{(1)},...,{\mathcal{M}}_{\mathbf{I}}^{(N_{\mathbf{I}})})$$
其中$s_{{\mathcal{M}}_{\mathbf{I}}^{(1)}}>s_{{\mathcal{M}}_{\mathbf{I}}^{(N_{\mathbf{I}})}}$
然后，对于像素 $p$：
当 $s_{{\mathbf{M}}_{\mathbf{I}}^{(i)}}<s$ 时，$\mathbf{V}(s,\mathbf{p})$ 的第 $i$ 个分量被设置为 ${\mathbf{M}}_{\mathbf{I}}^{(i)}(\mathbf{P})$；

当 $s_{{\mathbf{M}}_{\mathbf{I}}^{(i)}}\ge s$ 时，$\mathbf{V}(s,\mathbf{p})$ 的第 $i$ 个分量被设置为 1 的充要条件是：

${\mathbf{M}}_{\mathbf{I}}^{(i)}(\mathbf{P})=1$ 并且在所有更小的掩膜集合 {MI(j)∣s≤sMI(j)<sMI(i)}\{ \mathbf{M}_\mathbf{I}^{(j)}|s≤s_{\mathbf{M}_\mathbf{I}^{(j)}}<s_{\mathbf{M}_\mathbf{I}^{(i)}} \}{MI(j)​∣s≤sMI(j)​​<sMI(i)​​} 中的掩膜在像素p上的取值均为0。
公式化如下：
$$\begin{array}{rl}& {\mathbf{V}}^i(s,\mathbf{p})=\{\begin{array}{ll}{\mathbf{M}}_{\mathbf{I}}^{(i)}(\mathbf{p})& \text{ if }{s}_{{\mathbf{M}}_{\mathbf{I}}^{(i)}}<s\text{ or }\mathcal{C}(\mathbf{p})\\ 0& \text{ otherwise }\end{array}\\ & \mathcal{C}(\mathbf{p})\triangleq \left(\forall \mathbf{M}\in \left\{{\mathbf{M}}_{\mathbf{I}}^{(j)}\mid s\le s_{{\mathbf{M}}_{\mathbf{I}}^{(j)}}<s_{{\mathbf{M}}_{\mathbf{I}}^{(i)}}\right\},\mathbf{M}(\mathbf{p})=0\right)\end{array}$$

上述像素身份向量的分配基于以下事实：如果一个像素在给定尺度下属于某个mask，那么在较大尺度下它仍属于该mask。

损失函数

对尺度门控高斯亲和特征的训练采用对应蒸馏损失（Correspondence Distillation Loss）。
在给定尺度 $s$ 下，两个像素 ${\mathbf{p}}_1$、${\mathbf{p}}_2$之间的掩膜对应关系为：
$${\mathrm{Corr}}_m\left(s,{\mathbf{p}}_1,{\mathbf{p}}_2\right)=1\left(\mathbf{V}\left(s,{\mathbf{p}}_1\right)\cdot \mathbf{V}\left(s,{\mathbf{p}}_2\right)\right)$$

其中 $1(\cdot )$ 是指示函数，当输入大于等于0时取值为1。
两个像素之间的特征对应关系定义为它们尺度门控特征的余弦相似度：
$${\mathrm{Corr}}_f\left(s,{\mathbf{p}}_1,{\mathbf{p}}_2\right)=⟨{\mathbf{F}}^s\left({\mathbf{p}}_1\right),{\mathbf{F}}^s\left({\mathbf{p}}_2\right)⟩.$$

两个像素之间的对应蒸馏损失为：
$$\begin{array}{rl}{\mathcal{L}}_{\text{corr }}\left(s,{\mathbf{p}}_1,{\mathbf{p}}_2\right)=& \left(1-2\cdot {\mathrm{Corr}}_m\left(s,{\mathbf{p}}_1,{\mathbf{p}}_2\right)\right)\\ & \cdot \max \left({\mathrm{Corr}}_f\left(s,{\mathbf{p}}_1,{\mathbf{p}}_2\right),0\right)\end{array}$$

特征范数正则化

训练时，二维特征通过使用3D亲和特征进行渲染得到。这揭示了2D特征和3D特征之间的错位。2D特征是若干三维特征的线性组合，每个三维特征具有不同的方向。在此类情形下，可能在渲染后的特征图上表现出良好的分割能力，但在三维空间中的表现却不理想，这促使引入特征范数正则化。

具体地，在渲染2D特征图时，3D特征首先被归一化为单位向量。

在引入特征范数正则化项后，SAGA的总损失定义为：
$$\mathcal{L}=\sum _{\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)\in \delta (\mathbf{I})\times \delta (\mathbf{I})}{\mathcal{L}}_{\text{corr }}\left({\mathbf{p}}_1,{\mathbf{p}}_2\right)+\sum _{\mathbf{p}\in \delta (\mathbf{I})}{\mathcal{L}}_{\text{norm }}(\mathbf{p}),$$
这里 $\delta (\mathbf{I})$ 代表图像内的像素集合。

附加训练策略

训练过程中数据不平衡是一个不可避免的问题，表现为：

1. 多数像素对在尺度变化下仍然保持positive或negative，使学习到的特征对尺度不敏感；
2. 绝大多数像素对呈负相关，导致特征塌缩；
3. 在图像中占据更多像素的大目标对优化的影响更大，造成对小目标分割性能不佳。

为解决这些问题，采用对像素进行重采样并对不同样本的损失函数进行重新加权的策略。

3.5 推理

在训练好的高斯亲和特征基础上，SAGA可以在三维空间执行多种分割任务。对于提示式分割，SAGA以特定视图下的二维点提示和尺度作为输入。然后，通过将尺度门控的三维高斯亲和特征和从渲染特征图中根据点提示选取的2D查询特征进行匹配，来对三维目标进行分割。对于自动场景分解，SAGA直接在三维空间中使用HDBSCAN对亲和特征进行聚类。

另外，还涉及了一种基于投票的分割机制，将SAGA和CLIP结合起来进行开放词汇分割。

Experiments