从递归到迭代的全方位解析——力扣38.外观数列（Count and Say）

---

【LeetCode】38. 外观数列（Count and Say）——从递归到迭代的全方位解析（Java详解）

---

一、题目描述

题目链接：LeetCode 38. Count and Say

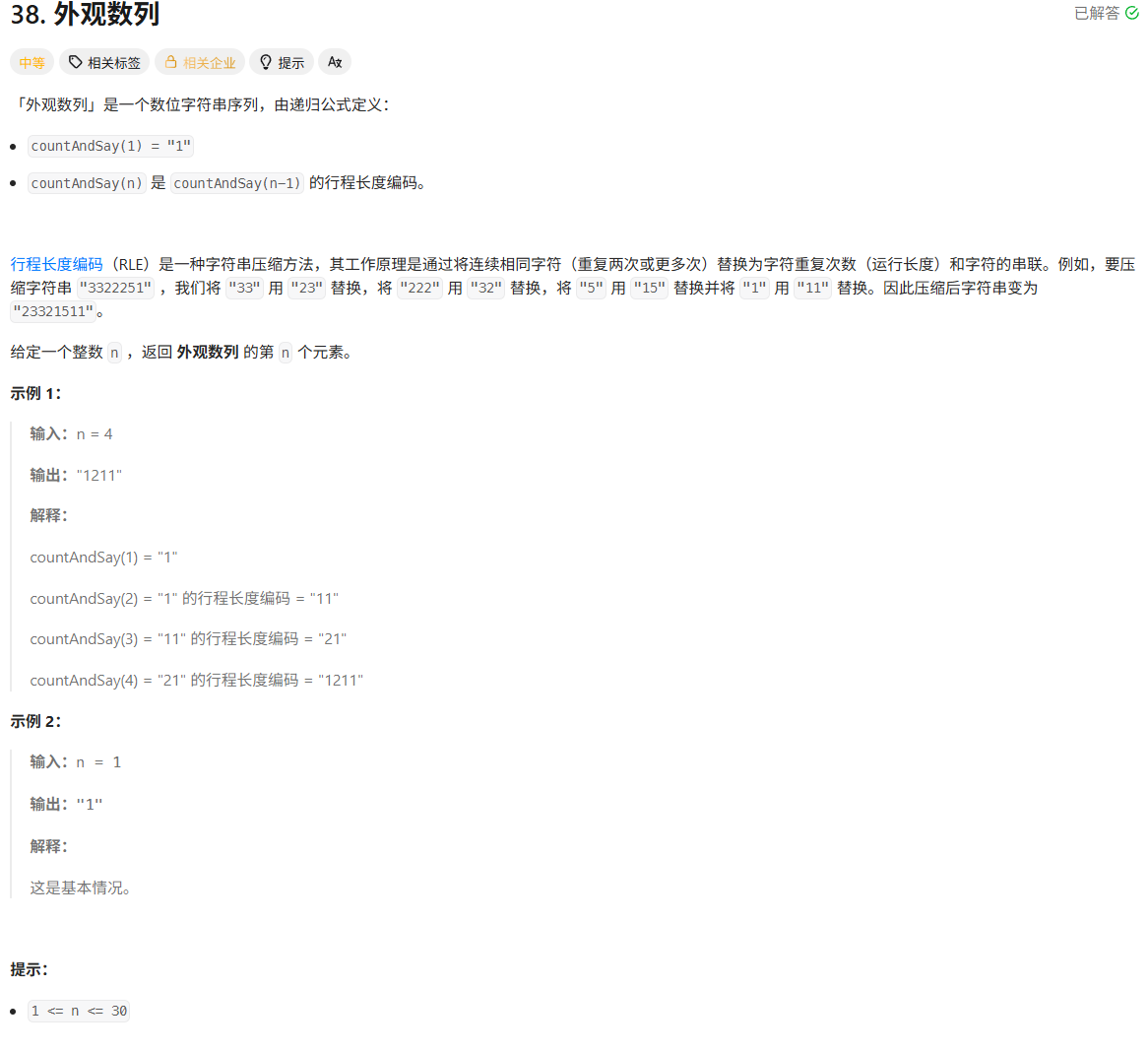
“外观数列”（Count and Say）是一个特殊的数位字符串序列，定义如下：

countAndSay(1) = "1"
countAndSay(n) = 对 countAndSay(n - 1) 进行“行程长度编码（RLE）”得到。

其中，“行程长度编码”指将连续相同的数字用「出现次数 + 数字」的形式表示。

例如：

"3322251" → "23321511"

解释：

• “33” → “23”
• “222” → “32”
• “5” → “15”
• “1” → “11”

拼接结果即为 "23321511"。

---

二、示例

示例 1：

输入：n = 4
输出："1211"解释：
countAndSay(1) = "1"
countAndSay(2) = "11"    （一个 1）
countAndSay(3) = "21"    （两个 1）
countAndSay(4) = "1211"  （一个 2，一个 1）

示例 2：

输入：n = 1
输出："1"

---

三、思路分析

1. 规律总结

外观数列是一种「读数描述」序列：

• 第 1 项为 “1”
• 每一项通过读出前一项的数字规律生成下一项

例如：

1 → 11 → 21 → 1211 → 111221 → 312211 → ...

2. 解法分类

可以使用两种方式求解：

1. 递归法 —— 按定义直接递归生成。
2. 迭代法 —— 从底向上逐步构造结果，更高效。

---

四、方法一：递归实现

思路

根据题目定义：

countAndSay(n) = 对 countAndSay(n - 1) 进行压缩编码

因此可以直接递归调用自身，当 n == 1 时返回 “1”。

Java 实现

public class Solution {public String countAndSay(int n) {// 基础情况if (n == 1) return "1";// 递归获得上一项String prev = countAndSay(n - 1);// 将上一项转换为本项StringBuilder sb = new StringBuilder();int count = 1;for (int i = 1; i <= prev.length(); i++) {if (i == prev.length() || prev.charAt(i) != prev.charAt(i - 1)) {sb.append(count).append(prev.charAt(i - 1));count = 1;} else {count++;}}return sb.toString();}
}

复杂度分析

• 时间复杂度：O(n × m)，其中 m 为字符串长度。
• 空间复杂度：O(n)，递归深度为 n。

---

五、方法二：迭代实现（推荐）

思路

• 从 “1” 开始；
• 每次根据前一项生成下一项；
• 循环 n - 1 次即可。

Java 实现

public class Solution {public String countAndSay(int n) {if (n <= 0) return "";String result = "1";// 从第2项开始构造for (int i = 2; i <= n; i++) {result = getNext(result);}return result;}// 根据上一项字符串生成下一项private String getNext(String s) {StringBuilder sb = new StringBuilder();int count = 1;for (int i = 1; i <= s.length(); i++) {if (i == s.length() || s.charAt(i) != s.charAt(i - 1)) {sb.append(count).append(s.charAt(i - 1));count = 1;} else {count++;}}return sb.toString();}
}

优势

• 无递归调用，逻辑更直观。
• 适合 n 较大的情况（如 n = 30）。

---

六、方法三：字符数组优化（高性能版）

思路

在上一种迭代思路基础上，我们可以避免频繁 StringBuilder 拼接，通过预分配空间提升性能。

Java 实现

public class Solution {public String countAndSay(int n) {if (n <= 0) return "";String result = "1";for (int i = 2; i <= n; i++) {char[] chars = result.toCharArray();StringBuilder sb = new StringBuilder();int count = 1;for (int j = 1; j <= chars.length; j++) {if (j == chars.length || chars[j] != chars[j - 1]) {sb.append(count).append(chars[j - 1]);count = 1;} else {count++;}}result = sb.toString();}return result;}
}

该实现逻辑清晰、性能较优，适合面试中书写。

---

七、运行示例

输入 n	输出
1	1
2	11
3	21
4	1211
5	111221
6	312211

---

八、总结

实现方式	思想	优点	缺点
递归法	按定义直接实现	简单直观	递归层数深，性能较差
迭代法	从底向上生成	高效、可控	代码稍长
数组优化	字符遍历优化	性能最好	实现最复杂

推荐优先使用迭代实现，逻辑清晰且无栈风险。

---