深度学习(DL)概念及实例操作
深度学习是机器学习的一个子领域,它使用包含多个处理层的神经网络来学习和表示数据的复杂模式。简单来说,就是让计算机通过"深度"的神经网络来模拟人脑的学习过程。
一、"深度"的理解?
-
浅层网络:只能学习简单的线性或近似线性关系
-
深层网络:可以学习复杂的非线性关系,逐层提取特征
-
底层:学习基础特征(如边缘、颜色)
-
中层:组合基础特征(如形状、纹理)
-
高层:识别复杂模式(如物体、场景)
-
二、神经网络基础:
神经元 (Neuron) | 类似于我们大脑中的基本组成单元,在收到输入的信号之后,神经元通过处理,然后把结果输出给其它的神经元或者直接作为最终的输出。 |
权重/加权 (Weights) | 每个输入将会存在着一个与之相应的权重因子。在初始化网络的时候,这些权重会被随机设置,然后在训练模型的过程中再不断地发生更改。 训练过程中,一个输入具有的权重因子越高,意味着这个输入越重要,当权重因子为0时意味着这个输入是无价值的。 |
偏置/偏倚 (Bias) | 除了权重之外,输入还需要经过另外一种线性处理,叫做偏置。通过把偏置b与加权后的输入信号 X * W1 直接相加,以此作为激活函数的输入信号。 |
激活函数 | 上面线性处理之后的输入信号通过激活函数进行非线性变换,从而得到输出信号。即最后输出的信号具有 f(X * W1 + b)的形式,其中 f( ) 为激活函数。 |
上述可简化为:
输入 → 加权求和 → 激活函数 → 输出
↓ ↓ ↓ ↓
(,
) →
*
+
*
+ b → f(∑) → y
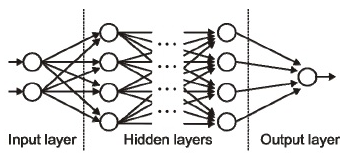
输入层/输出层/隐藏层
输入层代表接受输入数据的一层,基本上是网络的第一层;
输出层是产生输出的一层,或者是网络的最后一层;
网络中间的处理层叫做隐藏层。
多层感知器 (MLP-Multi Layer Perceptron)
将多个神经元堆叠起来工作进而产生有用的输出
三、主要神经网络类型
前馈神经网络(FNN) | 输入层 → 隐藏层1 → 隐藏层2 → ... → 输出层 |
卷积神经网络(CNN)—— 主要用于图像处理 | 输入图像 → 卷积层 → 池化层 → 卷积层 → 全连接层 → 输出 |
循环神经网络(RNN)—— 用于序列数据 | 时间步1 → 时间步2 → 时间步3 → ... ↓ ↓ ↓ 隐藏状态 → 隐藏状态 → 隐藏状态 |
Transformer —— 现代NLP的主流架构 | 输入 → 位置编码 → 多头注意力 → 前馈网络 → 输出 特点:自注意力机制、并行处理、长距离依赖) |
四、深度学习的关键技术
先认识下面几个重要的概念
成本函数 (cost function)
神经网络的目标是增加预测的准确性从而减少误差,即最小化成本函数。
常见的算法有:
(1)均方误差作为成本误差,即表示为 C= 1/m ∑(y – a)2 , 其中m是训练过程中输入数据的个数,a是相应的预测值,y代表实际值。
(2)梯度下降(gradient descent):从起始点x开始,一次移动一点,如此重复下去,直到达到局部的极小值,此时认为极小值就是成本最小的地方。
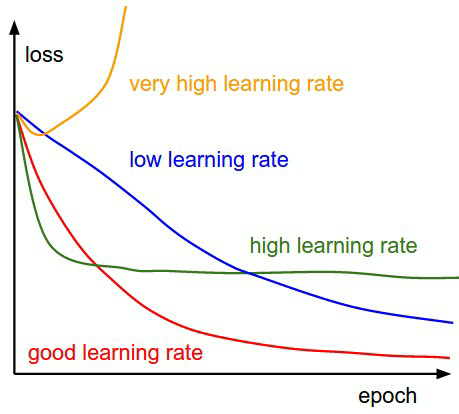
学习速率 (Learning Rate)
学习速率定义为在每次迭代过程中对成本函数的最小化次数。简单来说,学习速率就是指朝着成本函数最小值的下降速率。选择学习速率需要很谨慎,过大会导致可能越过最优解,过小会导致收敛花费太多的时间。
整个深度学习的关键分为以下几点:
传播算法 | for 每个训练批次: 前向传播:计算预测值 计算损失:predicted vs actual 反向传播:计算梯度 ∂loss/∂weight 更新权重:weight = weight - lr * gradient |
分批 (Batches) | 将数据随机地分为几个大小一致的数据块,再分批次输入,分批训练能够使模型的适用性更好 。 |
周期 (epochs) | 一个周期表示对所有的数据批次都进行了一次迭代,包括一次正向传播和一次反向传播。往往周期数越高,模型的准确性就越高,但是,耗时往往就越长。同时还需要考虑次数过高可能会出现过拟合的情况。 |
激活函数 | ReLU: f(x) = max(0, x) Sigmoid: f(x) = 1/(1+e^(-x)) Tanh: f(x) = (e^x - e^(-x))/(e^x + e^(-x)) Softmax: 用于多分类输出 |
优化器 | (常见的优化算法) SGD: W = W - lr * ∇W Momentum: 考虑历史梯度方向 Adam: 自适应学习率 + Momentum |
五、深度学习工作流程
数据准备 | 数据收集 → 数据清洗 → 数据增强 → 标准化 → 划分训练/验证/测试集 |
模型设计 | if 图像分类: 使用CNN(ResNet, VGG) if 文本处理: 使用Transformer(BERT, GPT) if 时序预测: 使用LSTM或Transformer if 推荐系统: 使用深度矩阵分解 |
训练与调优 | 超参数调优: 学习率、批大小、网络深度、Dropout率、正则化强度 |
评估与部署 | 模型评估指标: 准确率、精确率、召回率、F1分数、AUC-ROC(分类) MSE、MAE、R²(回归 |
总结:神经网络是由大量彼此相连、概念化的人造神经元组成的,这些神经元彼此之间传递着数据,相应的权重也会随着神经网络的经历而进行调整。神经元们有着激活的阈值,当它们遇到相应的数据以及权重时会被激活,这些被激活的神经元组合起来导致了“学习”行为的产生。
六、示例操作
本例来自下面链接,原代码有些小错误,我对代码进行了部分修改:https://mbd.baidu.com/newspage/data/dtlandingsuper?nid=dt_4054819818344122608&sourceFrom=search_a
例子内容:展示神经网络如何学习数学函数——神经网络正在学习如何从输入 预测输出
,通过调整数百万个内部参数,逐渐逼近这个三次函数的形状。
## 1、导入模块
import torch
import torch.nn as nn # 导入PyTorch的神经网络模块
import torch.optim as optim # 导入PyTorch的优化器模块
import matplotlib.pyplot as plt # 导入matplotlib用于绘制图表
import numpy as np # 导入numpy用于生成数据## 2、数据准备
x = np.linspace(-10,10,1000) #生成1000个等间距的点,从-10到10
y = x ** 3 # 对应输出y = x^3# 将numpy数组转化为Pytorch张量
x_train = torch.tensor(x,dtype=torch.float32).unsqueeze(1) ## 将x转化为二维的浮点型张量y_train = torch.tensor(y,dtype=torch.float32).unsqueeze(1) ## 将y转化为二维的浮点型张量## 3、模型定义--定义简单的神经网络
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()self.layer1 = nn.Linear(1, 128) # 输入1个特征,输出128个神经元self.layer2 = nn.Linear(128, 128) # 隐藏层,输入128,输出128self.layer3 = nn.Linear(128, 1) # 输出层,输入128个特征,输出1个值def forward(self, x):# ReLU激活函数:引入非线性,让网络能够学习复杂模式x = torch.relu(self.layer1(x)) ## 第一层 + ReLU激活x = torch.relu(self.layer2(x)) ## 第二层 + ReLU激活x = self.layer3(x) # 输出层(无激活函数,因为这是回归问题)return x## 4、训练设置
# 初始化模型、损失函数和优化器
model = SimpleNN() # 创建模型实例#使用均方误差(MSE)作为损失函数(MSELoss:均方误差,适合回归问题 loss = (预测值 - 真实值)² 的平均值)
criterion = nn.MSELoss()
# Adam优化器,学习率设为0.001
optimizer = optim.Adam(model.parameters(), lr=0.001)epochs = 2000 # 训练轮数
losses = [] # 记录每轮的损失值# 训练循环
for epoch in range(epochs):outputs = model(x_train) # 前向传播:得到预测值loss = criterion(outputs, y_train)# 计算损失值(预测值和真实值的差异)optimizer.zero_grad() # 将所有参数的梯度清零,以免之前的梯度累加loss.backward() # 反向传播,计算每个参数的梯度optimizer.step() # 优化器更新模型的参数losses.append(loss.item()) # 记录损失值# 每100轮打印一次损失if (epoch + 1) % 100 ==0:print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')## 5、结果可视化
# 绘制损失曲线
plt.figure(figsize=(12, 4))plt.subplot(1, 2, 1)
plt.plot(losses) # 回执损失值曲线
plt.title('Loss during training') #设置图表标题
plt.xlabel('Epoch') # X轴标签
plt.ylabel('Loss') # y轴标签
plt.grid(True) #显示网格# 进行预测并绘制对比图
plt.subplot(1, 2, 2)
with torch.no_grad(): # 禁用梯度计算,节省内存predicted = model(x_train).numpy() # 得到最终预测结果# 绘制实际值和预测值
plt.scatter(x, y, label='Actual', color='blue', s=1) # 真实值(蓝色)
plt.scatter(x, predicted, label='Predicted', color='red', s=1) # 预测值(红色)
plt.title('Model Prediction vs Actual') #设置图表标题
plt.legend() #设置图例
plt.grid(True)plt.tight_layout() #自动调整布局
plt.show() #显示图表
输出结果:
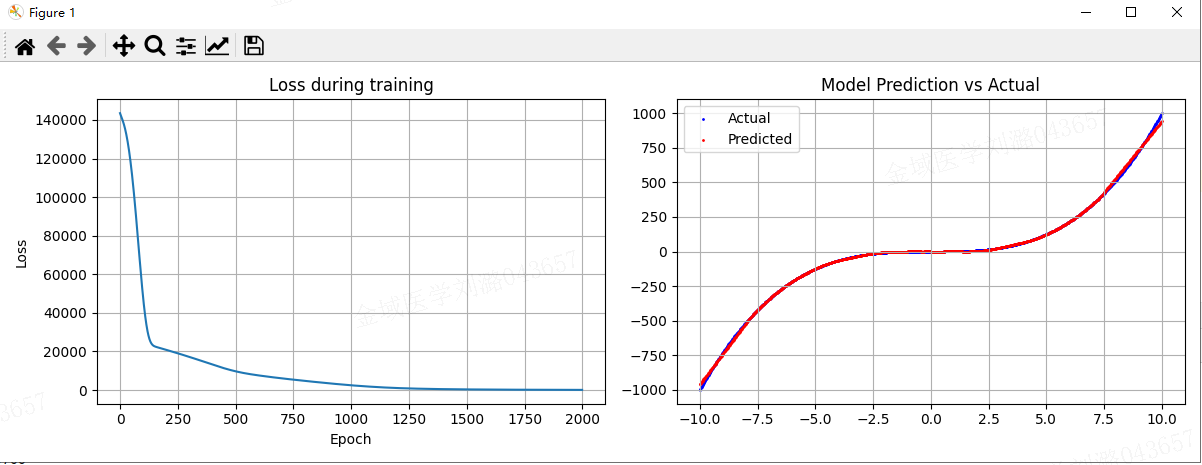
上面代码展示了深度学习的基本流程:数据准备 → 模型定义 → 训练 → 评估,这是所有深度学习项目的基础模式。
