当前位置：首页 > news >正文

深度学习入门（二）——反向传播与向量化推导

news 2025/10/12 6:58:45

一、前言：梯度从哪来？

在第一篇里，我们讲过神经元和前向传播。
我们知道一个神经网络的基本结构：输入经过层层加权求和、非线性激活，最后得到输出。
接着通过损失函数计算误差。

但在实际训练时，模型不是“知道答案”的。
它只能根据输出和真实标签之间的**误差（Loss）**来判断：我做得对不对。
问题是，它该如何知道“哪里错了、错了多少、怎么改”？

答案就是：反向传播（Backpropagation）。

反向传播的作用是：

告诉每个参数该往哪个方向调、调多少，才能让整体误差下降。

这就是神经网络能够自我学习的关键机制。
而实现这一点的基础，就是梯度。

二、梯度的本质：变化的方向

我们先不急着讲复杂公式，先回到一个直觉问题：
当我们说“一个函数的梯度”时，它到底是什么？

在一维情况下，函数 f(x)f(x)f(x) 的梯度其实就是导数 f′(x)f'(x)f′(x)，代表斜率。
如果 f′(x)>0f'(x) > 0f′(x)>0，我们要让函数变小，就往反方向（负方向）走一点。
这就是最朴素的梯度下降法。

在多维情况下，梯度就是偏导数的向量：

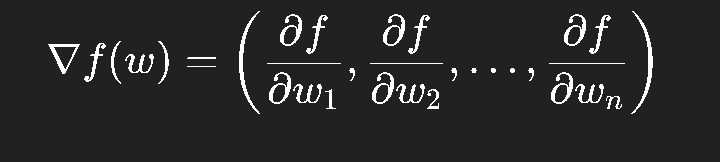
它指向函数增大的最快方向。
所以想让函数减小，就朝反方向走。

在神经网络中，每个参数 www 都参与损失的计算。
反向传播要做的，就是求出每个 www 对整体损失 LLL 的偏导数 ∂L∂w\frac{\partial L}{\partial w}∂w∂L。

如果你能算出这个梯度，你就能训练模型。

三、前向传播回顾：信息是如何流动的

让我们先复习一个最简单的三层网络（输入层 → 隐藏层 → 输出层）：

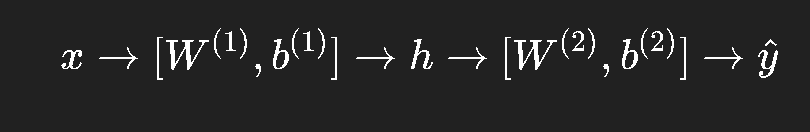
它的计算流程是：

隐藏层输入：
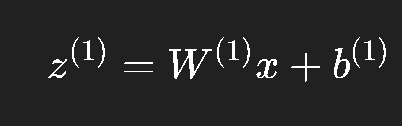
隐藏层输出（激活）：
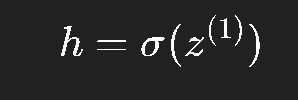
输出层输入：
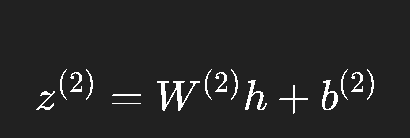
输出层输出（预测）：
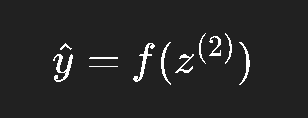
损失函数：

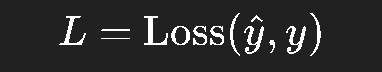
整个计算是从左到右的：输入 → 线性变换 → 激活 → 线性变换 → 输出。
这叫 前向传播（Forward Propagation）。

但要更新参数，我们要知道“每个参数改动后，Loss 怎么变”。
也就是说，我们需要从输出往回传递“误差信息”——这就是反向传播。

四、链式法则：反向传播的核心

如果你只想记住反向传播的一句话，那就是——

反向传播 = 链式法则的系统应用。

链式法则告诉我们：如果一个变量依赖于另一个变量，那么它们的导数可以层层传递。

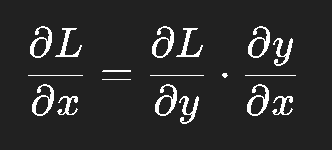
在神经网络中，层与层之间正好符合这种依赖关系：

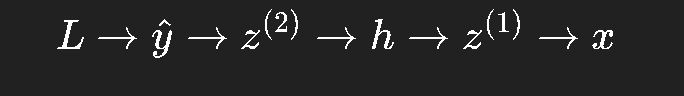
因此可以通过链式法则一步步地把误差从输出层传回输入层。
每一层都只需要知道“自己输出的梯度”和“当前的局部导数”，就能求出“输入的梯度”。

这就是为什么反向传播算法能在复杂的多层结构中高效传播梯度。

五、反向传播的推导：一层一层地来

我们以刚才那三层网络为例，推导每一层的梯度。

1. 输出层

损失函数 LLL 对输出 y^\hat{y}y^ 的导数：

比如使用平方误差损失：

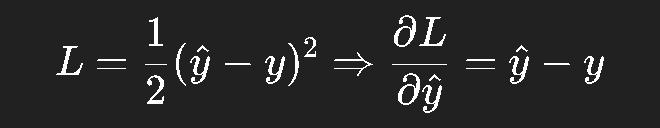
再往前一层：

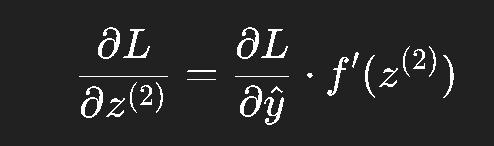
因为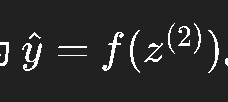

然后对参数求导：

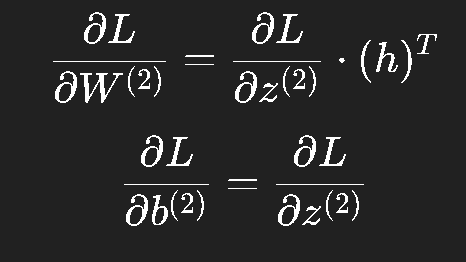
再往前传：

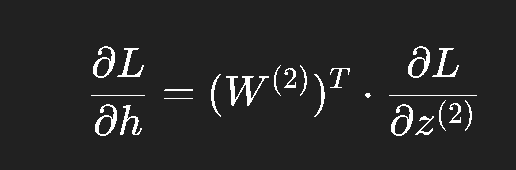
2. 隐藏层

隐藏层的输出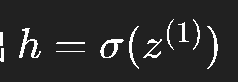

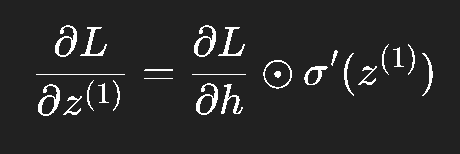
其中 “⊙\odot⊙” 表示元素级乘法。

然后：

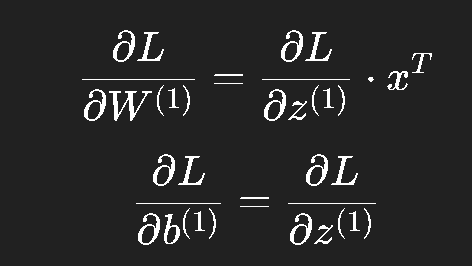
这就完成了从输出层到输入层的一次完整反向传播。

六、伪代码演示：一步步实现 BP 算法

我们可以把上面的推导写成伪代码：

# 前向传播
z1 = W1 @ x + b1
h = sigmoid(z1)
z2 = W2 @ h + b2
y_hat = z2  # 假设线性输出
loss = 0.5 * (y_hat - y)**2# 反向传播
dL_dyhat = y_hat - y
dL_dz2 = dL_dyhat * 1.0           # 因为 y_hat = z2
dL_dW2 = dL_dz2 @ h.T
dL_db2 = dL_dz2
dL_dh = W2.T @ dL_dz2
dL_dz1 = dL_dh * h * (1 - h)
dL_dW1 = dL_dz1 @ x.T
dL_db1 = dL_dz1# 参数更新
W1 -= lr * dL_dW1
b1 -= lr * dL_db1
W2 -= lr * dL_dW2
b2 -= lr * dL_db2

这个过程本质上就是矩阵形式的链式法则。
每一层只需要知道“上层传来的梯度”，再乘上本层的导数，就能求得自己的梯度。

七、向量化思想：从标量推导到矩阵运算

在上面的推导中，如果你仔细看，会发现每个变量其实都可以是向量或矩阵。
这就是**向量化（Vectorization）**的意义。

为什么要向量化？

因为在深度学习中，数据往往是批量的。
我们不可能一个样本一个样本地算梯度，否则计算效率太低。
GPU 的强大之处就是能同时对成千上万个样本做矩阵运算。

比如批量大小为 BBB，输入维度为 nnn，那么：

则整个前向传播可以写成：

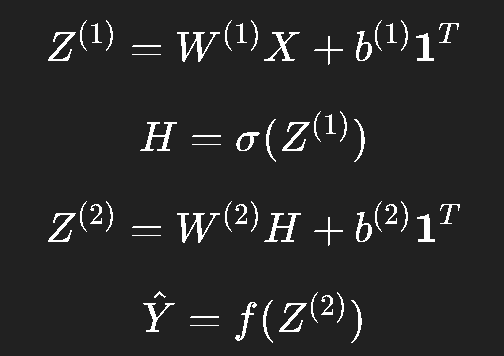
反向传播同样用矩阵表示：

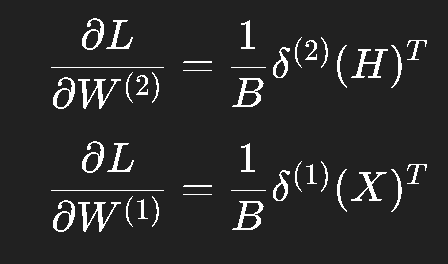
其中：

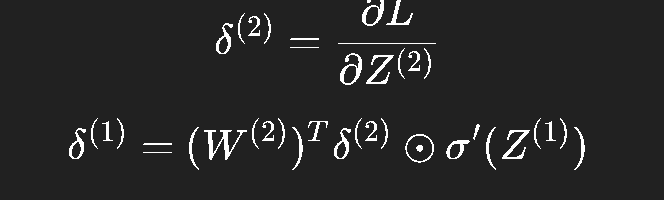
这种表示方式非常紧凑，而且与现代深度学习框架（如 PyTorch、TensorFlow）的实现完全一致。

八、数值稳定性与梯度爆炸/消失

理解反向传播的过程中，你可能听过两个著名的问题：
梯度消失（Vanishing Gradient） 和 梯度爆炸（Exploding Gradient）。

它们都与链式法则的“乘法效应”有关。

假设网络有很多层，每一层都有导数。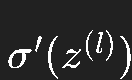
那么梯度传回输入层时是这些导数的连乘积：

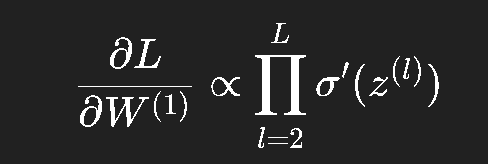
如果这些导数平均小于 1（如 sigmoid），那么乘积会迅速趋近 0，导致梯度几乎消失。
如果大于 1，则可能迅速膨胀，导致梯度爆炸。

这两个问题都会让训练变得极不稳定。

常见的解决办法包括：

使用 ReLU 激活（避免梯度饱和）；
使用合适的权重初始化（如 Xavier、He 初始化）；
对梯度进行裁剪（gradient clipping）。

九、从理论到工程：反向传播是如何实现的？

在框架层面，反向传播是通过**计算图（Computational Graph）**自动完成的。

简单来说，框架在前向传播时会记录每个操作的输入、输出和导数规则；
然后在反向阶段，根据依赖关系自动应用链式法则。

伪代码大概这样：

# 自动求导的基本逻辑
def backward(node):if node.grad is None:node.grad = 0for parent, local_grad in node.dependencies:parent.grad += node.grad * local_gradbackward(parent)

这就是 PyTorch 的 autograd 机制背后的核心思想。
因此我们在写网络时不需要手动写出每一层的导数，框架会帮我们自动完成。