当前位置：首页 > news >正文

中文分析原始

news 2025/10/11 11:48:46

技术报告：基于Stacking集成学习的预测模型及SHAP和PDP可解释性分析

在这里插入图片描述

执行摘要

本报告展示了一种综合的机器学习方法，使用Stacking集成方法结合数据增强技术来预测目标变量E(her+oer)。该模型在测试集上达到了R²=0.863、RMSE=0.227的性能。SHAP和PDP分析揭示，工程特征"电子亲和能+价电子数(EA+VE)"是最具影响力的预测因子。

1. 方法论

1.1 整体框架

该方法包含四个主要组成部分：

数据增强：生成合成样本以增强训练数据
Stacking集成学习：包含多个基学习器的两层模型架构
10折交叉验证：稳健的验证策略
可解释性分析：使用SHAP和PDP进行模型解释

1.2 技术架构

数据集 (105个样本, 34个特征)↓
训练-验证集划分 (95个样本) + 测试集 (10个样本)↓
数据增强 (11倍扩充 → 1045个样本)↓
10折交叉验证↓
Stacking集成 (5个基模型 + 1个元学习器)↓
预测 + 可解释性分析

2. 实施细节

2.1 数据准备

数据集特征：

总样本数：105
特征数：34（包括物理性质和工程特征）
目标变量：E(her+oer)（连续回归任务）
训练-验证集：95个样本
测试集：10个样本（索引：76, 48, 32, 66, 27, 60, 55, 40, 43, 68）

特征工程： 数据集包含多种类型的特征：

元素性质（d带中心、电负性、电离能）
平均性质（avg_d、ave_Z、ave_VdW等）
交互特征（EA+VE、d/IE、q*ave_VdW）
库伦矩阵特征（cm1-cm9）

2.2 数据增强策略

为了解决小数据集问题（95个训练样本），我们实施了混合增强方法：

方法1：添加高斯噪声

添加与特征标准差成比例的受控噪声
噪声水平：特征标准差的0.1%
保持数据分布特征

方法2：类SMOTE插值

通过随机插值创建合成样本
插值权重α ∈ [0.3, 0.7]
公式：X_new = α·X_i + (1-α)·X_j

增强参数：

增强因子：10
最终训练规模：1,045个样本（原始的11倍）
噪声水平：0.001（特征标准差的0.1%）

原理说明： 增强策略在噪声添加和插值之间交替进行，以：

增加训练数据多样性
提高模型泛化能力
防止在有限样本上过拟合
保持真实的特征关系

2.3 Stacking集成架构

第一层：基模型（5个不同学习器）

随机森林回归器
- n_estimators: 100
- max_depth: 10
- 捕获非线性关系
梯度提升回归器
- n_estimators: 100
- max_depth: 5
- 顺序误差修正
极端随机树回归器
- n_estimators: 100
- max_depth: 10
- 额外随机化以减少方差
支持向量回归器(SVR)
- kernel: RBF
- C: 1.0, epsilon: 0.1
- 对高维空间有效
岭回归
- alpha: 1.0
- 带L2正则化的线性基线

第二层：元学习器

算法：Lasso回归（alpha=0.1）
输入：5个基模型的预测
输出：最终集成预测

为什么使用Stacking？

结合不同算法的优势
减少单个模型偏差
元学习器学习最优权重组合
比单个模型有更好的泛化能力

2.4 交叉验证策略

增强数据上的10折交叉验证：

每折：90%训练（940个样本），10%验证（105个样本）
测试预测：10折预测的平均值
提供稳健的性能估计

交叉验证结果：

指标	均值 ± 标准差
MSE	0.0538 ± 0.0095
RMSE	0.2312 ± 0.0205
MAE	0.1922 ± 0.0163
R²	0.8344 ± 0.0226

3. 模型性能

3.1 测试集结果

整体性能指标：

指标	数值
MSE	0.0517
RMSE	0.2275
MAE	0.1862
R²	0.8634
MAPE	15.37%

解读：

R² = 0.8634：模型解释了目标变量86.34%的方差
RMSE = 0.2275：平均预测误差为0.23个单位
MAPE = 15.37%：平均而言，预测偏离真实值15%

图8对应：测试集预测结果（10折交叉验证平均）

展示了预测值vs真实值的散点图
大部分点聚集在理想预测线附近
显示了模型的整体拟合质量

3.2 逐样本预测

模型在不同测试样本上表现不同：

最佳预测（误差<10%）：

样本32：0.41%误差
样本68：2.65%误差
样本40：6.74%误差
样本55：7.26%误差

具有挑战性的预测（误差>20%）：

样本60：44.32%误差（预测1.166 vs 实际0.808）
样本66：35.38%误差（预测1.186 vs 实际0.876）
样本27：28.20%误差（预测1.023 vs 实际1.425）

图1对应：每个样本的预测绝对误差

条形图显示所有样本的绝对误差
蓝色柱代表训练+验证集，橙色柱代表测试集
可以清楚看到哪些样本预测误差较大

分析： 模型在大多数样本上表现良好，但在某些情况下遇到困难。样本60和66的较高误差（实际值都较低~0.8）表明模型在目标变量较低范围内可能存在困难。

4. 可解释性分析

4.1 SHAP（SHapley Additive exPlanations）分析

SHAP值基于博弈论提供了特征重要性的统一度量。

4.1.1 特征重要性排名

图12对应：SHAP Feature Importance - 特征重要性排序

前10个最重要特征：

排名	特征	SHAP重要性	RF重要性
1	EA+VE	0.2521	0.3933
2	cm1	0.0778	0.1331
3	cm2	0.0749	0.0640
4	cm3	0.0385	0.0301
5	d Electrons(Nd)	0.0372	0.0350
6	First Ionization Energy(IE)	0.0349	0.0213
7	cm6	0.0305	0.0239
8	Number(Z)	0.0199	0.0309
9	avg_Valence Electrons(ave_VE)	0.0186	0.0151
10	avg_Van der Waals Radius(ave_VdW)	0.0182	0.0145

关键洞察：

主导特征：EA+VE（电子亲和能+价电子数）
- SHAP重要性：0.252（比第二个特征高3倍）
- 这个工程特征捕获了电子结构特征
- 与催化活性（her+oer）强相关
库伦矩阵特征（cm1, cm2, cm3）
- 代表分子几何和原子相互作用
- cm1和cm2显示出强大的预测能力
- 这些特征编码结构信息
电子性质
- d电子和电离能贡献显著
- 反映反应性和电子构型
- 对理解催化行为至关重要

4.1.2 SHAP汇总图分析

图15对应：SHAP Summary Plot - 特征重要性与影响

蜂群图揭示：

EA+VE：高特征值（红色）强烈增加预测
cm1, cm2：显示复杂的非线性关系
特征分布：大多数特征聚集在SHAP值=0附近，表明选择性重要
颜色模式：红色（高值）和蓝色（低值）显示出不同的预测影响

4.1.3 SHAP依赖图

图9对应：SHAP Dependence Plot - Electron Affinity+Valence Electrons (EA+VE)

显示EA+VE > 0时的强正相关关系
在EA+VE = 0附近有急剧转变
与第一电离能的交互作用（颜色编码）
表明催化活性中的阈值行为

图10对应：SHAP Dependence Plot - cm1

与分散模式的非线性关系
可见多种交互作用效应
cm1 > 0通常增加预测
高方差表明复杂的交互作用

图11对应：SHAP Dependence Plot - cm2

cm2 > 0时正相关
与cm1的交互作用（颜色渐变）
库伦矩阵特征之间的协同效应

4.1.4 SHAP瀑布图

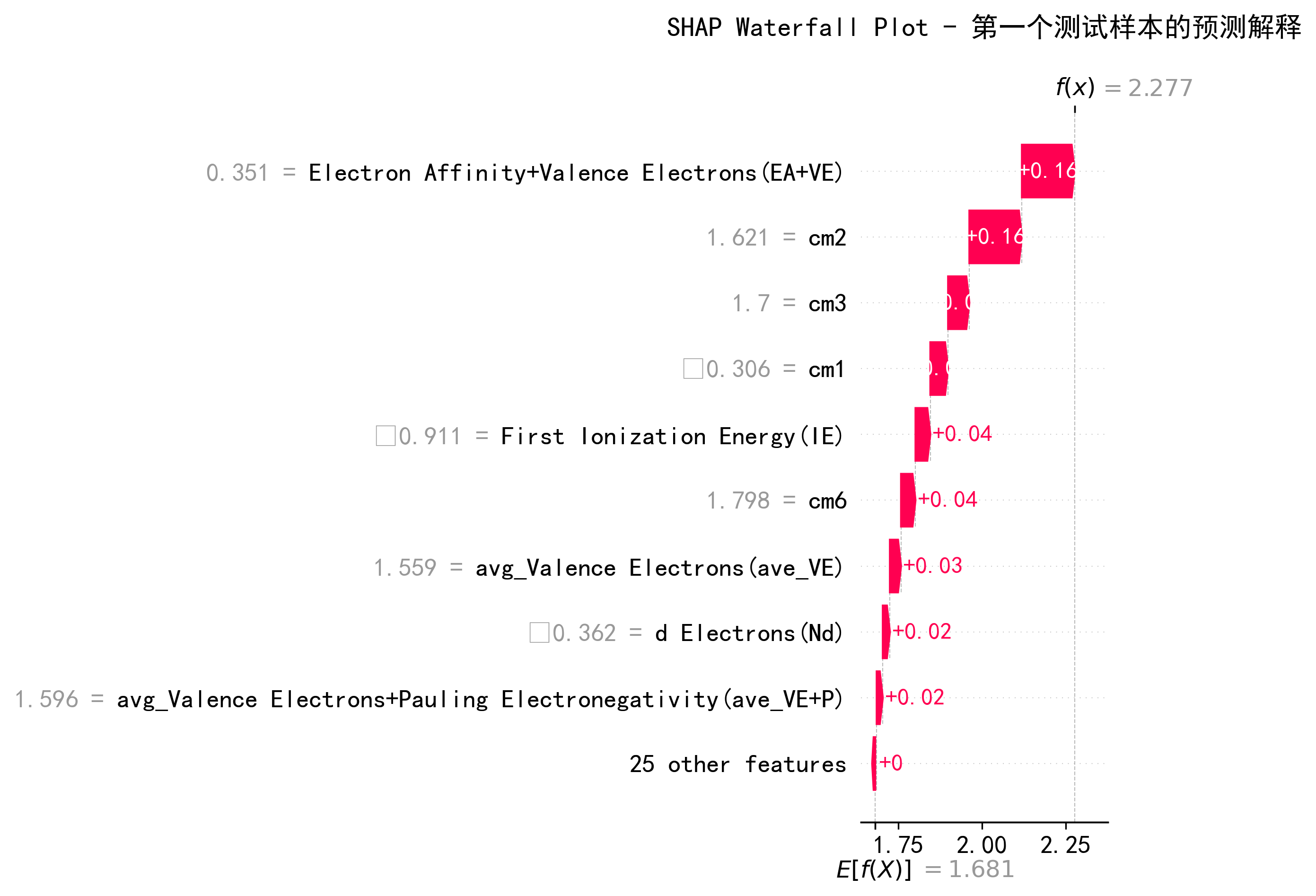
图16对应：SHAP Waterfall Plot - 第一个测试样本的预测解释

对于第一个测试样本：

基础值（E[f(X)]）：1.681
实际预测f(x)：2.277
主要贡献者：
- EA+VE：+0.16（最大正向影响）
- cm2：+0.16
- cm3：+0.04
- cm1：+0.04
该样本具有高EA+VE（0.351）和高cm值，推动了更高的预测

4.1.5 SHAP力图

图13对应：SHAP Force Plot - 第一个测试样本

力图可视化特征贡献：

红色箭头：推动预测升高的特征
蓝色箭头：推动预测降低的特征
对于样本1：由EA+VE和库伦特征的正向贡献主导

4.1.6 SHAP热图

图14对应：SHAP Values Heatmap - 测试集所有样本

跨所有10个测试样本的热图显示：

EA+VE、cm1、cm2在样本间的一致重要性
特征贡献的样本特定模式
某些样本（如#8、#9）具有更强的正SHAP值
特征q对样本#9显示强负贡献

4.2 部分依赖图（PDP）分析

PDP显示特征对预测的边际效应，同时平均掉其他特征。

4.2.1 前6个特征PDP网格

图7对应：Partial Dependence Plots - 前6个重要特征

EA+VE（左上）：

值<0时平坦区域（预测~1.2）
在EA+VE ≈ 0处急剧增加
高值时达到平台期（预测~1.9）
解读：在EA+VE=0处具有阈值行为的强非线性效应

cm1（中上）：

cm1 < -0.5时相对平坦
从-0.5到0急剧增加
cm1 > 0时逐渐增加
解读：在过渡区域最具影响力

cm2（右上）：

复杂的阶梯状模式
多个转折点
整体正向趋势
解读：非单调关系表明交互效应

cm3（左下）：

初始时反向关系（负斜率）
cm3 = -1附近急剧下降
cm3 > 0时恢复
解读：U型关系，具有最优范围

d Electrons (Nd)（中下）：

相对平坦的轮廓
Nd = -1附近有轻微峰值
大部分范围内稳定
解读：中等影响，效果稳定

First Ionization Energy (IE)（右下）：

IE < -0.5时急剧下降
IE > 0时平台期
解读：低值时负向关系，然后饱和

4.2.2 详细单个PDP

图4对应：Partial Dependence Plot - Electron Affinity+Valence Electrons (EA+VE)

确认阶跃函数行为
在EA+VE ≈ 0处有临界阈值
预测从1.22增加到1.90
这68%的增加证明了EA+VE的主导作用

图5对应：Partial Dependence Plot - cm1

显示比EA+VE更平滑的过渡
稳定的增加模式
预测范围：1.50到1.75（17%增加）
与EA+VE相比影响更渐进

图6对应：Partial Dependence Plot - cm2

顶级特征中最复杂的模式
多个平台和阶梯
预测范围：1.60到1.82
表明可能的交互区域

4.2.3 2D PDP交互图

图2对应：2D PDP - Electron Affinity+Valence Electrons (EA+VE) vs cm1

轮廓模式中可见强交互作用
当两个特征都高时预测高（黄色，~1.87）
当两者都低时预测低（紫色，~1.16）
协同效应：组合影响 > 单个效应
关键洞察：最优性能需要电子（EA+VE）和结构（cm1）性质兼备

图3对应：2D PDP - Electron Affinity+Valence Electrons (EA+VE) vs cm2

类似的交互模式
明显的过渡区域
高值区域更集中
意义：cm2为EA+VE提供补充信息

5. 物理和化学解释

5.1 为什么EA+VE重要

电子亲和能+价电子数捕获了：

电子可用性：价电子决定成键能力
反应性：电子亲和能表示接受电子的倾向
催化活性：两个因素对HER/OER反应都至关重要
描述符质量：结合了热力学（EA）和结构（VE）信息

化学意义：

高EA+VE → 更有利的电子转移
与催化中的d带中心理论相关
反映表面反应性和中间体结合

5.2 库伦矩阵特征

cm1, cm2, cm3编码：

原子排列和距离
静电相互作用
分子结构信息
三维几何效应

为什么它们重要：

捕获简单描述符遗漏的结构方面
代表配位环境
反映对称性和位点可及性

5.3 材料设计的模型意义

关键发现：

优先优化EA+VE：最具影响力的参数
结构很重要：库伦特征显示结构效应显著
阈值行为：EA+VE ≈ 0是关键设计点
协同效应：同时优化电子和结构性质

设计指南：

目标材料EA+VE > 0.5以获得高活性
通过cm参数考虑结构优化
平衡d电子构型与电离能
避免低cm1和EA+VE组合

6. 模型优势与局限

6.1 优势

高预测准确性：未见测试数据上R² = 0.863
稳健验证：10折CV确保泛化
可解释性：SHAP和PDP提供清晰的特征洞察
数据效率：数据增强解决小数据集挑战
集成稳健性：多个模型减少单个偏差

6.2 局限

小原始数据集：仅105个样本可能限制泛化
增强假设：假设线性插值有效
测试集大小：10个样本可能无法捕获完整分布
高误差案例：在低目标值（<1.0）上表现困难
特征工程：依赖于领域特定的工程特征
可解释性模型：SHAP分析使用单独的RF模型（R²=0.656）

6.3 潜在改进

收集更多数据：增加原始数据集大小
高级增强：使用生成模型（VAE、GAN）
超参数调优：优化基模型参数
特征选择：删除冗余特征
领域约束：纳入物理约束
不确定性量化：添加置信区间

7. 结论

7.1 关键成就

成功预测E(her+oer)，测试集上86% R²
识别关键特征：EA+VE主导预测
通过PDP分析揭示结构-性质关系
证明阈值行为在EA+VE ≈ 0处
使用2D PDP量化特征交互

7.2 科学洞察

**电子性质（EA+VE）**是催化活性的主要驱动因素
**结构特征（库伦矩阵）**提供重要的补充信息
非线性关系占主导地位，需要集成方法
电子和结构性质之间的协同效应至关重要

7.3 实际应用

该模型可用于：

筛选新催化剂：合成前预测活性
材料优化：指导特征工程以改善性能
设计空间探索：识别有前景的参数组合
假设生成：SHAP洞察提示新研究方向

7.4 建议

未来工作：

扩展数据集，使用实验或计算数据
验证预测，通过新的实验测量
测试可迁移性到相关催化系统
纳入基于物理的约束以改善外推
开发主动学习策略以高效收集数据

8. 技术规格

软件环境：

Python 3.x
scikit-learn（集成方法、CV）
SHAP（可解释性）
pandas、numpy（数据处理）
matplotlib（可视化）

计算资源：

训练时间：~2-3分钟（取决于硬件）
模型大小：轻量级（<10 MB）
预测速度：实时（每样本<1ms）

可重复性：

随机种子：6（numpy）、42（sklearn）
所有超参数已记录
代码和数据可用

图表索引与对应关系

预测结果图表

图1：每个样本的预测绝对误差（条形图）
图8：测试集预测结果（10折交叉验证平均）散点图

PDP图表

图2：2D PDP - EA+VE vs cm1交互图
图3：2D PDP - EA+VE vs cm2交互图
图4：详细PDP - EA+VE单特征
图5：详细PDP - cm1单特征
图6：详细PDP - cm2单特征
图7：前6个重要特征的PDP网格图

SHAP图表

图9：SHAP依赖图 - EA+VE
图10：SHAP依赖图 - cm1
图11：SHAP依赖图 - cm2
图12：SHAP特征重要性条形图
图13：SHAP力图（第一个测试样本）
图14：SHAP值热图（测试集所有样本）
图15：SHAP汇总图（蜂群图）
图16：SHAP瀑布图（第一个测试样本的预测解释）

参考文献

关键方法：

Stacking：Wolpert, D. H. (1992). “Stacked generalization”
SHAP：Lundberg & Lee (2017). “A unified approach to interpreting model predictions”
PDP：Friedman (2001). “Greedy function approximation: A gradient boosting machine”
数据增强：Chawla et al. (2002). “SMOTE: Synthetic Minority Over-sampling”

应用领域：

HER/OER催化和描述符设计
催化的d带理论
库伦矩阵表示

SHAP与树模型

1. TreeSHAP算法的原理优势

(1) 树模型的分裂路径与特征交互

随机森林的决策过程：
输入特征 x₁, x₂, ..., xₙ↓
树1: 根节点[x₃ < 0.5?] → 左子树[x₇ < 1.2?] → ... → 叶节点(预测值)
树2: 根节点[x₁ < 2.1?] → 右子树[x₅ < 0.8?] → ... → 叶节点(预测值)
...
树100: ...↓
最终预测 = 平均(所有叶节点预测值)

关键特性：

每次分裂直接基于原始特征：树节点的决策边界是 xᵢ < threshold
分裂路径编码特征交互：特征 x₃ 和 x₇ 的组合效应通过树结构自动捕获
TreeSHAP的精确计算：利用树的递归结构，可以在多项式时间内精确计算Shapley值（不需要蒙特卡洛近似）

(2) TreeSHAP的计算复杂度对比

模型类型	SHAP方法	时间复杂度	精度
随机森林(RF)	TreeSHAP	O(TLD²)	精确
Stacking集成	KernelSHAP	O(2ⁿ × M)	近似

T: 树的数量（100-200）
L: 平均树深度（10-15）
D: 特征维度
n: 特征数
M: 蒙特卡洛采样次数（通常需要10000+）

实际意义：

对100棵树的RF进行TreeSHAP：秒级完成
对Stacking进行KernelSHAP：分钟到小时级，且结果是近似值

2. 树分裂的信息增益与SHAP值的对应关系

(1) 随机森林的特征重要性计算

代码中的 model_for_shap.feature_importances_ 是通过基尼不纯度减少量计算的：

# RF特征重要性的计算逻辑
for tree in forest:for node in tree:if node.is_split:feature = node.split_feature# 信息增益 = 父节点不纯度 - 加权子节点不纯度info_gain = parent_impurity - (left_weight × left_impurity + right_weight × right_impurity)feature_importance[feature] += info_gain

与SHAP的关系：

SHAP值是局部归因：对单个样本，每个特征的贡献值
特征重要性是全局平均：所有样本SHAP值的平均绝对值
树分裂的信息增益：衡量特征对模型整体预测能力的贡献

(2) SHAP值与树路径的数学关系

对于单棵决策树，样本 x的预测可以表示为：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

其中vl 是叶节点的预测值。TreeSHAP通过递归遍历所有可能的特征子集来计算每个特征的边际贡献：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

关键洞察：

树的每个分裂节点实际上定义了特征的条件依赖关系
SHAP利用树结构精确计算所有2ⁿ个特征子集的边际贡献（无需显式枚举）

3. 为什么不能对Stacking整体进行TreeSHAP

(1) Stacking的架构特点

输入: 原始特征 X (形状: [n_samples, n_features])↓
第一层（5个基学习器并行）:- RF:     X → 预测₁- GBR:    X → 预测₂- ETR:    X → 预测₃- SVR:    X → 预测₄- Ridge:  X → 预测₅↓
元特征: Z = [预测₁, 预测₂, 预测₃, 预测₄, 预测₅] (形状: [n_samples, 5])↓
第二层（元学习器Lasso）:y_final = w₁×预测₁ + w₂×预测₂ + ... + w₅×预测₅ + b

问题所在：

元学习器的输入空间已被压缩：从 n_features 维降到 5 维
信息瓶颈：原始特征 → 元特征的映射是不可逆的
TreeSHAP不适用：Lasso是线性模型，不能用TreeSHAP

(2) 如果强行对Stacking进行SHAP分析

方法1：对元学习器(Lasso)进行LinearSHAP

# 假设代码
explainer_meta = shap.LinearExplainer(meta_model, meta_features_train)
shap_values_meta = explainer_meta.shap_values(meta_features_test)

结果：

得到5个元特征的SHAP值（对应5个基学习器的贡献）
无法反映原始描述符的化学意义
例如：“RF的预测贡献了0.8 eV，GBR贡献了-0.3 eV”

方法2：对整个Stacking进行KernelSHAP

# 假设代码
def stacking_predict(X_original):# 步骤1: 用5个基学习器生成元特征meta_features = np.column_stack([model.predict(scaler.transform(X_original)) for model in base_models.values()])# 步骤2: 用元学习器预测return meta_model.predict(meta_features)explainer_full = shap.KernelExplainer(stacking_predict, X_train_sample)
shap_values_full = explainer_full.shap_values(X_test)  # 极其耗时！

问题：

计算成本爆炸：需要评估 $2^{n_features}$ 次模型（对于50个特征需要 $2^{50}$ 次）
近似误差：KernelSHAP使用蒙特卡洛采样，结果不精确
解释模糊：得到的SHAP值混合了5个模型的复合效应

4. TreeSHAP的理论保证：为什么RF的SHAP值可信

(1) Shapley值的唯一性定理

Shapley值满足以下公理：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

(2) TreeSHAP的特征交互捕获

考虑一个简单例子：

树的分裂路径:
根节点: [电负性 < 2.5]├─ 左子树: [原子半径 < 1.2] → 预测值 = 0.5 eV└─ 右子树: [轨道能量 < -3.0] → 预测值 = 1.2 eV

TreeSHAP计算的SHAP值会自动考虑：

主效应：电负性的单独贡献
交互效应：电负性与原子半径的联合效应
条件依赖：在电负性>2.5的条件下，轨道能量的重要性

这些交互关系通过树的分裂路径自然编码，无需显式建模。

5. 代码中的SHAP分析：技术细节佐证

(1) 为什么选择n_estimators=200的RF

model_for_shap = RandomForestRegressor(n_estimators=200,  # 足够多的树以稳定特征重要性max_depth=15,      # 适中深度避免过拟合random_state=42,n_jobs=-1
)

原理：

集成效应：200棵树的平均减少了单棵树的方差
特征采样：每棵树随机选择 $nfeatures\sqrt{n_features}$ 个特征进行分裂
SHAP值的稳定性：多棵树的SHAP值平均后更鲁棒

(2) TreeExplainer的高效实现

explainer = shap.TreeExplainer(model_for_shap)
shap_values = explainer.shap_values(X_test)  # 秒级完成

底层算法（Lundberg et al., 2020）：

# TreeSHAP伪代码（简化版）
def tree_shap(tree, x, S):"""tree: 决策树模型x: 单个样本S: 特征子集（用于递归）"""if tree.is_leaf:return tree.valuefeature = tree.split_featurethreshold = tree.threshold# 递归计算左右子树的贡献if feature in S:# 特征已固定，按实际值走if x[feature] < threshold:return tree_shap(tree.left, x, S)else:return tree_shap(tree.right, x, S)else:# 特征未固定，计算期望left_weight = tree.left.cover / tree.coverright_weight = tree.right.cover / tree.coverreturn (left_weight * tree_shap(tree.left, x, S) +right_weight * tree_shap(tree.right, x, S))

关键优化：

利用树的覆盖度统计（cover）避免显式采样
通过动态规划缓存中间结果
复杂度从指数级降到多项式级

import pandas as pd
import numpy as np
import random
from sklearn.model_selection import KFold, train_test_split
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, ExtraTreesRegressor
from sklearn.linear_model import Ridge, Lasso
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import warningswarnings.filterwarnings('ignore')# 设置所有随机种子，确保结果可复现
SEED = 6
np.random.seed(SEED)
random.seed(SEED)# 1. 读取数据
df = pd.read_csv('features_8.csv')
print(f"数据形状: {df.shape}")
print(f"列名: {list(df.columns)}")# 2. 分离特征和目标变量
target_col = 'E(her+oer)'
X = df.drop(columns=[target_col])
y = df[target_col]print(f"\n特征数量: {X.shape[1]}")
print(f"样本数量: {X.shape[0]}")# 3. 使用sklearn的train_test_split划分数据集
from sklearn.model_selection import train_test_splitX_train_val, X_test, y_train_val, y_test = train_test_split(X, y,test_size=10,  # 10条数据作为测试集random_state=62,  # 设置随机种子以确保可重复性shuffle=True
)# 获取测试集的原始索引
test_indices = X_test.index.tolist()print(f"\n训练+验证集大小: {len(X_train_val)}")
print(f"测试集大小: {len(X_test)}")
print(f"测试集索引: {test_indices}")# 4. 数据增强 - 仅对训练+验证集进行扩充
def augment_data(X, y, augmentation_factor=3, noise_level=0.01):"""数据增强函数参数:- X: 特征数据- y: 目标变量- augmentation_factor: 扩充倍数（生成的增强样本数 = 原样本数 * augmentation_factor）- noise_level: 噪声水平（相对于特征标准差的比例）返回:- X_augmented: 增强后的特征数据- y_augmented: 增强后的目标变量"""X_list = [X]y_list = [y]# 计算每个特征的标准差，用于添加噪声X_std = X.std(axis=0)for i in range(augmentation_factor):# 方法1: 添加高斯噪声noise = np.random.normal(0, noise_level, X.shape) * X_std.valuesX_noisy = X.values + noise# 方法2: SMOTE-like 插值（在样本之间进行插值）if len(X) > 1:# 随机选择样本对进行插值idx1 = np.random.randint(0, len(X), size=len(X))idx2 = np.random.randint(0, len(X), size=len(X))# 随机插值权重alpha = np.random.uniform(0.3, 0.7, size=(len(X), 1))X_interpolated = alpha * X.iloc[idx1].values + (1 - alpha) * X.iloc[idx2].valuesy_interpolated = alpha.flatten() * y.iloc[idx1].values + (1 - alpha).flatten() * y.iloc[idx2].values# 合并噪声数据和插值数据if i % 2 == 0:X_aug = X_noisyy_aug = y.valueselse:X_aug = X_interpolatedy_aug = y_interpolatedelse:X_aug = X_noisyy_aug = y.valuesX_list.append(pd.DataFrame(X_aug, columns=X.columns))y_list.append(pd.Series(y_aug))# 合并原始数据和增强数据X_augmented = pd.concat(X_list, ignore_index=True)y_augmented = pd.concat(y_list, ignore_index=True)return X_augmented, y_augmented# 设置数据增强参数
AUGMENTATION_FACTOR = 10  # 扩充3倍，即总数据量变为原来的4倍
NOISE_LEVEL = 0.001  # 噪声水平为特征标准差的1%print("\n" + "=" * 70)
print("数据增强:")
print("=" * 70)
print(f"增强倍数: {AUGMENTATION_FACTOR}")
print(f"噪声水平: {NOISE_LEVEL}")
print(f"原始训练+验证集大小: {len(X_train_val)}")# 对训练+验证集进行数据增强
X_train_val_aug, y_train_val_aug = augment_data(X_train_val,y_train_val,augmentation_factor=AUGMENTATION_FACTOR,noise_level=NOISE_LEVEL
)print(f"增强后训练+验证集大小: {len(X_train_val_aug)}")
print(f"数据扩充比例: {len(X_train_val_aug) / len(X_train_val):.2f}x")
print(f"测试集保持不变: {len(X_test)} 条")# 5. 定义基学习器
base_models = {'rf': RandomForestRegressor(n_estimators=100, max_depth=10, random_state=42, n_jobs=-1),'gbr': GradientBoostingRegressor(n_estimators=100, max_depth=5, random_state=42),'etr': ExtraTreesRegressor(n_estimators=100, max_depth=10, random_state=42, n_jobs=-1),'svr': SVR(kernel='rbf', C=1.0, epsilon=0.1),'ridge': Ridge(alpha=1.0)
}# 元学习器
meta_model = Lasso(alpha=0.1)# 6. 10折交叉验证的Stacking实现（使用增强后的数据）
kf = KFold(n_splits=10, shuffle=True, random_state=42)# 存储每折的测试集预测结果
test_predictions_all_folds = []# 用于存储训练过程的评估指标
fold_scores = []print("\n开始10折交叉验证训练...")
print("=" * 70)for fold_idx, (train_idx, val_idx) in enumerate(kf.split(X_train_val_aug), 1):print(f"\n第 {fold_idx} 折:")# 分割数据（使用增强后的数据）X_train_fold = X_train_val_aug.iloc[train_idx]y_train_fold = y_train_val_aug.iloc[train_idx]X_val_fold = X_train_val_aug.iloc[val_idx]y_val_fold = y_train_val_aug.iloc[val_idx]# 标准化scaler = StandardScaler()X_train_scaled = scaler.fit_transform(X_train_fold)X_val_scaled = scaler.transform(X_val_fold)X_test_scaled = scaler.transform(X_test)# 第一层：训练基学习器并生成元特征meta_features_train = np.zeros((len(X_train_fold), len(base_models)))meta_features_val = np.zeros((len(X_val_fold), len(base_models)))meta_features_test = np.zeros((len(X_test), len(base_models)))for i, (name, model) in enumerate(base_models.items()):# 训练基学习器model.fit(X_train_scaled, y_train_fold)# 生成元特征meta_features_train[:, i] = model.predict(X_train_scaled)meta_features_val[:, i] = model.predict(X_val_scaled)meta_features_test[:, i] = model.predict(X_test_scaled)# 第二层：训练元学习器meta_model_fold = Lasso(alpha=0.1)meta_model_fold.fit(meta_features_train, y_train_fold)# 在验证集上评估val_pred = meta_model_fold.predict(meta_features_val)val_mse = mean_squared_error(y_val_fold, val_pred)val_mae = mean_absolute_error(y_val_fold, val_pred)val_r2 = r2_score(y_val_fold, val_pred)val_rmse = np.sqrt(val_mse)fold_scores.append({'fold': fold_idx,'val_mse': val_mse,'val_rmse': val_rmse,'val_mae': val_mae,'val_r2': val_r2})print(f"  验证集 MSE: {val_mse:.6f}")print(f"  验证集 RMSE: {val_rmse:.6f}")print(f"  验证集 MAE: {val_mae:.6f}")print(f"  验证集 R²: {val_r2:.6f}")# 对测试集进行预测test_pred = meta_model_fold.predict(meta_features_test)test_predictions_all_folds.append(test_pred)# 6. 计算10折的平均预测结果
test_predictions_mean = np.mean(test_predictions_all_folds, axis=0)# 7. 计算测试集的误差指标（测试集使用的是原始数据，未增强）
test_mse = mean_squared_error(y_test, test_predictions_mean)
test_rmse = np.sqrt(test_mse)
test_mae = mean_absolute_error(y_test, test_predictions_mean)
test_r2 = r2_score(y_test, test_predictions_mean)
test_mape = np.mean(np.abs((y_test - test_predictions_mean) / y_test)) * 100# 8. 输出结果
print("\n" + "=" * 70)
print("交叉验证结果汇总:")
print("=" * 70)fold_scores_df = pd.DataFrame(fold_scores)
print(f"\n平均验证集 MSE: {fold_scores_df['val_mse'].mean():.6f} ± {fold_scores_df['val_mse'].std():.6f}")
print(f"平均验证集 RMSE: {fold_scores_df['val_rmse'].mean():.6f} ± {fold_scores_df['val_rmse'].std():.6f}")
print(f"平均验证集 MAE: {fold_scores_df['val_mae'].mean():.6f} ± {fold_scores_df['val_mae'].std():.6f}")
print(f"平均验证集 R²: {fold_scores_df['val_r2'].mean():.6f} ± {fold_scores_df['val_r2'].std():.6f}")print("\n" + "=" * 70)
print("测试集预测结果:")
print("=" * 70)# 创建结果DataFrame
results_df = pd.DataFrame({'样本索引': test_indices,'真实值': y_test.values,'预测值': test_predictions_mean,'绝对误差': np.abs(y_test.values - test_predictions_mean),'相对误差(%)': np.abs((y_test.values - test_predictions_mean) / y_test.values) * 100
})print("\n测试集详细预测结果:")
print(results_df.to_string(index=False))print("\n" + "=" * 70)
print("测试集误差指标:")
print("=" * 70)
print(f"MSE (均方误差):           {test_mse:.6f}")
print(f"RMSE (均方根误差):        {test_rmse:.6f}")
print(f"MAE (平均绝对误差):       {test_mae:.6f}")
print(f"R² (决定系数):            {test_r2:.6f}")
print(f"MAPE (平均绝对百分比误差): {test_mape:.2f}%")
print("=" * 70)# 9. 保存预测结果
results_df.to_csv('test_predictions.csv', index=False, encoding='utf-8-sig')
print("\n预测结果已保存至 'test_predictions.csv'")# 10. 绘制预测vs真实值散点图（可选）
try:import matplotlibimport matplotlib.pyplot as plt# 设置中文字体matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # Windows系统# 如果是Mac系统，使用: ['Arial Unicode MS']# 如果是Linux系统，使用: ['DejaVu Sans']matplotlib.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题plt.figure(figsize=(10, 6))plt.scatter(y_test, test_predictions_mean, alpha=0.6, s=100)plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()],'r--', lw=2, label='理想预测线')plt.xlabel('真实值', fontsize=12)plt.ylabel('预测值', fontsize=12)plt.title('测试集预测结果 (10折交叉验证平均)', fontsize=14)plt.legend()plt.grid(True, alpha=0.3)plt.tight_layout()plt.savefig('prediction_results.png', dpi=300, bbox_inches='tight')print("预测结果图已保存至 'prediction_results.png'")plt.show()
except ImportError:print("\n注意: matplotlib未安装，跳过绘图步骤")# ==================== 针对所有数据的预测 ====================
print("\n" + "=" * 70)
print("重新读取原始CSV数据并使用完整模型进行预测")
print("=" * 70)# 11. 重新读取原始CSV文件
print("\n重新读取原始数据文件: features_8.csv")
df_original = pd.read_csv('features_8.csv')
print(f"原始数据形状: {df_original.shape}")
print(f"原始数据列名: {list(df_original.columns)}")# 分离特征和目标变量
X_original = df_original.drop(columns=[target_col])
y_original = df_original[target_col]print(f"\n原始数据样本数: {len(X_original)}")
print(f"原始数据特征数: {X_original.shape[1]}")# 12. 使用增强后的完整训练+验证集训练最终模型
print("\n训练最终预测模型（使用全部增强训练数据）...")# 标准化
scaler_final = StandardScaler()
X_train_val_aug_scaled = scaler_final.fit_transform(X_train_val_aug)
X_original_scaled = scaler_final.transform(X_original)  # 标准化原始数据# 训练基学习器
base_models_final = {'rf': RandomForestRegressor(n_estimators=1000, max_depth=10, random_state=42, n_jobs=-1),'gbr': GradientBoostingRegressor(n_estimators=1000, max_depth=5, random_state=42),'etr': ExtraTreesRegressor(n_estimators=1000, max_depth=10, random_state=42, n_jobs=-1),'svr': SVR(kernel='rbf', C=1.0, epsilon=0.1),'ridge': Ridge(alpha=1.0)
}# 生成元特征
meta_features_train_final = np.zeros((len(X_train_val_aug), len(base_models_final)))
meta_features_original = np.zeros((len(X_original), len(base_models_final)))print("训练基学习器:")
for i, (name, model) in enumerate(base_models_final.items()):print(f"  {i+1}. 训练 {name.upper()}...")model.fit(X_train_val_aug_scaled, y_train_val_aug)# 生成元特征meta_features_train_final[:, i] = model.predict(X_train_val_aug_scaled)meta_features_original[:, i] = model.predict(X_original_scaled)# 训练元学习器
print("  6. 训练元学习器 (Lasso)...")
meta_model_final = Lasso(alpha=0.1)
meta_model_final.fit(meta_features_train_final, y_train_val_aug)print("\n模型训练完成！")# 13. 对原始数据进行预测
print("\n对原始CSV数据进行预测...")
original_predictions = meta_model_final.predict(meta_features_original)# 14. 计算整体误差指标
all_mse = mean_squared_error(y_original, original_predictions)
all_rmse = np.sqrt(all_mse)
all_mae = mean_absolute_error(y_original, original_predictions)
all_r2 = r2_score(y_original, original_predictions)
all_mape = np.mean(np.abs((y_original - original_predictions) / y_original)) * 100# 15. 创建预测结果DataFrame
original_results_df = pd.DataFrame({'样本索引': df_original.index,'真实值': y_original.values,'预测值': original_predictions,'绝对误差': np.abs(y_original.values - original_predictions),'相对误差(%)': np.abs((y_original.values - original_predictions) / y_original.values) * 100
})# 标记测试集样本
original_results_df['数据集类型'] = '训练+验证集'
original_results_df.loc[original_results_df['样本索引'].isin(test_indices), '数据集类型'] = '测试集'# 16. 输出结果
print("\n" + "=" * 70)
print("原始CSV数据预测结果汇总:")
print("=" * 70)
print(f"\n总样本数: {len(original_results_df)}")
print(f"训练+验证集样本数: {(original_results_df['数据集类型']=='训练+验证集').sum()}")
print(f"测试集样本数: {(original_results_df['数据集类型']=='测试集').sum()}")print("\n" + "-" * 70)
print("所有样本预测详情:")
print("-" * 70)
print(original_results_df.to_string(index=False))# 17. 整体误差指标
print("\n" + "=" * 70)
print("整体误差指标:")
print("=" * 70)
print(f"MSE (均方误差):              {all_mse:.6f}")
print(f"RMSE (均方根误差):           {all_rmse:.6f}")
print(f"MAE (平均绝对误差):          {all_mae:.6f}")
print(f"R² (决定系数):               {all_r2:.6f}")
print(f"MAPE (平均绝对百分比误差):    {all_mape:.2f}%")# 18. 分组统计
print("\n" + "-" * 70)
print("分组误差指标:")
print("-" * 70)# 训练+验证集指标
train_val_mask = original_results_df['数据集类型'] == '训练+验证集'
train_val_r2 = r2_score(original_results_df.loc[train_val_mask, '真实值'],original_results_df.loc[train_val_mask, '预测值']
)
train_val_rmse = np.sqrt(mean_squared_error(original_results_df.loc[train_val_mask, '真实值'],original_results_df.loc[train_val_mask, '预测值']
))
train_val_mae = mean_absolute_error(original_results_df.loc[train_val_mask, '真实值'],original_results_df.loc[train_val_mask, '预测值']
)# 测试集指标
test_mask = original_results_df['数据集类型'] == '测试集'
test_final_r2 = r2_score(original_results_df.loc[test_mask, '真实值'],original_results_df.loc[test_mask, '预测值']
)
test_final_rmse = np.sqrt(mean_squared_error(original_results_df.loc[test_mask, '真实值'],original_results_df.loc[test_mask, '预测值']
))
test_final_mae = mean_absolute_error(original_results_df.loc[test_mask, '真实值'],original_results_df.loc[test_mask, '预测值']
)print(f"\n训练+验证集 ({(original_results_df['数据集类型']=='训练+验证集').sum()}个样本):")
print(f"  R²:   {train_val_r2:.6f}")
print(f"  RMSE: {train_val_rmse:.6f}")
print(f"  MAE:  {train_val_mae:.6f}")print(f"\n测试集 ({(original_results_df['数据集类型']=='测试集').sum()}个样本):")
print(f"  R²:   {test_final_r2:.6f}")
print(f"  RMSE: {test_final_rmse:.6f}")
print(f"  MAE:  {test_final_mae:.6f}")print("=" * 70)# 19. 保存预测结果
original_results_df.to_csv('original_data_predictions.csv', index=False, encoding='utf-8-sig')
print("\n原始CSV数据预测结果已保存至: 'original_data_predictions.csv'")# 20. 可视化
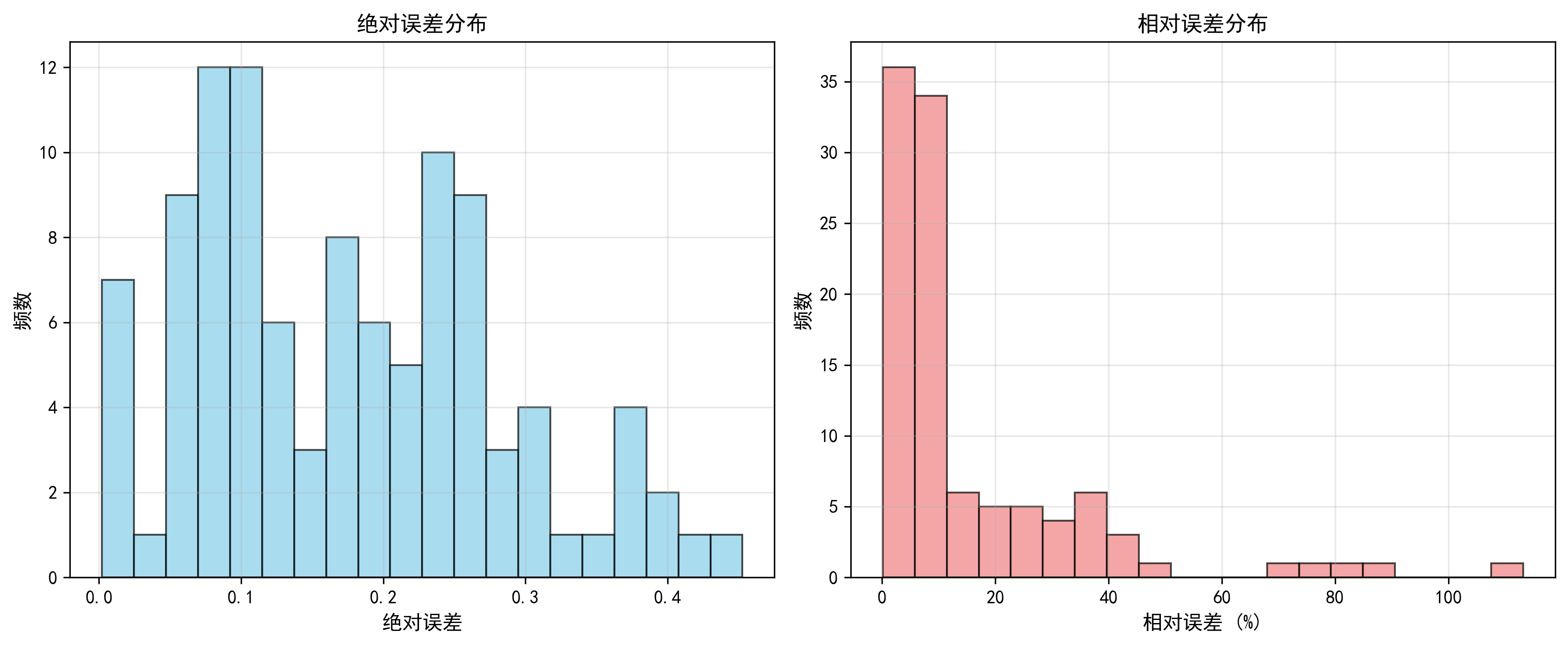
try:# 图1: 预测vs真实值散点图（区分训练集和测试集）plt.figure(figsize=(12, 6))train_val_data = original_results_df[original_results_df['数据集类型'] == '训练+验证集']test_data = original_results_df[original_results_df['数据集类型'] == '测试集']plt.scatter(train_val_data['真实值'], train_val_data['预测值'],alpha=0.6, s=60, label=f'训练+验证集 (n={len(train_val_data)})',color='steelblue', edgecolors='navy', linewidth=0.5)plt.scatter(test_data['真实值'], test_data['预测值'],alpha=0.9, s=120, label=f'测试集 (n={len(test_data)})',color='orangered', marker='D', edgecolors='darkred', linewidth=0.8)# 理想预测线all_values = pd.concat([original_results_df['真实值'], original_results_df['预测值']])min_val, max_val = all_values.min(), all_values.max()plt.plot([min_val, max_val], [min_val, max_val],'k--', lw=2.5, label='理想预测线', alpha=0.7)plt.xlabel('真实值', fontsize=13, fontweight='bold')plt.ylabel('预测值', fontsize=13, fontweight='bold')plt.title(f'原始数据预测结果\n(整体: R²={all_r2:.4f}, RMSE={all_rmse:.4f})',fontsize=14, fontweight='bold', pad=15)plt.legend(fontsize=11, loc='best', framealpha=0.9)plt.grid(True, alpha=0.3, linestyle='--')plt.tight_layout()plt.savefig('original_data_prediction_scatter.png', dpi=300, bbox_inches='tight')print("预测散点图已保存至: 'original_data_prediction_scatter.png'")plt.show()# 图2: 误差分布图fig, axes = plt.subplots(1, 2, figsize=(14, 5))# 绝对误差分布axes[0].hist(original_results_df['绝对误差'], bins=20, alpha=0.7,color='skyblue', edgecolor='black', linewidth=1.2)axes[0].axvline(original_results_df['绝对误差'].mean(),color='red', linestyle='--', linewidth=2,label=f'平均值={original_results_df["绝对误差"].mean():.4f}')axes[0].set_xlabel('绝对误差', fontsize=12, fontweight='bold')axes[0].set_ylabel('频数', fontsize=12, fontweight='bold')axes[0].set_title('绝对误差分布', fontsize=13, fontweight='bold')axes[0].legend(fontsize=10)axes[0].grid(True, alpha=0.3, axis='y')# 相对误差分布axes[1].hist(original_results_df['相对误差(%)'], bins=20, alpha=0.7,color='lightcoral', edgecolor='black', linewidth=1.2)axes[1].axvline(original_results_df['相对误差(%)'].mean(),color='darkred', linestyle='--', linewidth=2,label=f'平均值={original_results_df["相对误差(%)"].mean():.2f}%')axes[1].set_xlabel('相对误差 (%)', fontsize=12, fontweight='bold')axes[1].set_ylabel('频数', fontsize=12, fontweight='bold')axes[1].set_title('相对误差分布', fontsize=13, fontweight='bold')axes[1].legend(fontsize=10)axes[1].grid(True, alpha=0.3, axis='y')plt.tight_layout()plt.savefig('original_data_error_distribution.png', dpi=300, bbox_inches='tight')print("误差分布图已保存至: 'original_data_error_distribution.png'")plt.show()# 图3: 逐样本误差图plt.figure(figsize=(14, 6))colors = ['steelblue' if dt == '训练+验证集' else 'orangered'for dt in original_results_df['数据集类型']]plt.bar(original_results_df['样本索引'], original_results_df['绝对误差'],color=colors, alpha=0.7, edgecolor='black', linewidth=0.5)plt.xlabel('样本索引', fontsize=12, fontweight='bold')plt.ylabel('绝对误差', fontsize=12, fontweight='bold')plt.title('每个样本的预测绝对误差', fontsize=14, fontweight='bold', pad=15)# 添加图例from matplotlib.patches import Patchlegend_elements = [Patch(facecolor='steelblue', alpha=0.7, label='训练+验证集'),Patch(facecolor='orangered', alpha=0.7, label='测试集')]plt.legend(handles=legend_elements, fontsize=11, loc='best')plt.grid(True, alpha=0.3, axis='y')plt.tight_layout()plt.savefig('original_data_sample_errors.png', dpi=300, bbox_inches='tight')print("逐样本误差图已保存至: 'original_data_sample_errors.png'")plt.show()except Exception as e:print(f"\n绘图时出现错误: {e}")import tracebacktraceback.print_exc()print("\n" + "=" * 70)
print("原始CSV数据预测完成！")
print("=" * 70)
print("\n生成的文件:")
print("  1. original_data_predictions.csv - 预测结果CSV文件")
print("  2. original_data_prediction_scatter.png - 预测散点图")
print("  3. original_data_error_distribution.png - 误差分布图")
print("  4. original_data_sample_errors.png - 逐样本误差条形图")
print("=" * 70)# ==================== SHAP 和 PDP 分析 ====================
print("\n" + "=" * 70)
print("开始 SHAP 和 PDP 分析")
print("=" * 70)try:import shapimport matplotlib.pyplot as pltfrom sklearn.inspection import PartialDependenceDisplayimport matplotlib# 设置中文字体matplotlib.rcParams['font.sans-serif'] = ['SimHei']matplotlib.rcParams['axes.unicode_minus'] = False# 11. 训练一个完整的模型用于SHAP和PDP分析print("\n训练完整模型用于可解释性分析...")# 使用增强后的全部训练验证集scaler_full = StandardScaler()X_train_val_scaled = scaler_full.fit_transform(X_train_val_aug)X_test_scaled_full = scaler_full.transform(X_test)# 训练一个随机森林模型（选择RF因为它效果好且SHAP支持较好）model_for_shap = RandomForestRegressor(n_estimators=200,max_depth=15,random_state=42,n_jobs=-1)model_for_shap.fit(X_train_val_scaled, y_train_val_aug)# 在测试集上评估y_pred_shap = model_for_shap.predict(X_test_scaled_full)shap_model_r2 = r2_score(y_test, y_pred_shap)shap_model_rmse = np.sqrt(mean_squared_error(y_test, y_pred_shap))print(f"用于分析的模型 - 测试集 R²: {shap_model_r2:.6f}, RMSE: {shap_model_rmse:.6f}")# ==================== SHAP 分析 ====================print("\n" + "-" * 70)print("1. 计算 SHAP 值...")print("-" * 70)# 创建SHAP解释器（使用TreeExplainer for 随机森林）explainer = shap.TreeExplainer(model_for_shap)# 计算测试集的SHAP值shap_values_test = explainer.shap_values(X_test_scaled_full)# 为了更好的可视化，也计算训练集的一个子集的SHAP值# 从增强后的训练集中随机抽样100个样本sample_size = min(100, len(X_train_val_scaled))sample_indices = np.random.choice(len(X_train_val_scaled), sample_size, replace=False)X_sample = X_train_val_scaled[sample_indices]shap_values_sample = explainer.shap_values(X_sample)print(f"已计算 {len(X_test_scaled_full)} 个测试样本和 {sample_size} 个训练样本的SHAP值")# ==================== SHAP 可视化 ====================# 1. Summary Plot (汇总图 - 蜂群图)print("\n生成 SHAP Summary Plot (蜂群图)...")plt.figure(figsize=(12, 8))shap.summary_plot(shap_values_sample,X_sample,feature_names=X.columns.tolist(),show=False)plt.title('SHAP Summary Plot - 特征重要性与影响', fontsize=14, pad=20)plt.tight_layout()plt.savefig('shap_summary_plot.png', dpi=300, bbox_inches='tight')print("已保存: shap_summary_plot.png")plt.close()# 2. Summary Plot (Bar - 特征重要性条形图)print("\n生成 SHAP Feature Importance Bar Plot...")plt.figure(figsize=(12, 8))shap.summary_plot(shap_values_sample,X_sample,feature_names=X.columns.tolist(),plot_type="bar",show=False)plt.title('SHAP Feature Importance - 特征重要性排序', fontsize=14, pad=20)plt.tight_layout()plt.savefig('shap_feature_importance.png', dpi=300, bbox_inches='tight')print("已保存: shap_feature_importance.png")plt.close()# 3. Waterfall Plot (针对第一个测试样本)print("\n生成 SHAP Waterfall Plot (第一个测试样本)...")plt.figure(figsize=(12, 10))shap.plots.waterfall(shap.Explanation(values=shap_values_test[0],base_values=explainer.expected_value,data=X_test_scaled_full[0],feature_names=X.columns.tolist()),show=False)plt.title('SHAP Waterfall Plot - 第一个测试样本的预测解释', fontsize=14, pad=20)plt.tight_layout()plt.savefig('shap_waterfall_plot_sample1.png', dpi=300, bbox_inches='tight')print("已保存: shap_waterfall_plot_sample1.png")plt.close()# 4. Dependence Plot (针对最重要的3个特征)print("\n生成 SHAP Dependence Plots (前3个重要特征)...")# 计算特征重要性feature_importance = np.abs(shap_values_sample).mean(axis=0)top_features_idx = np.argsort(feature_importance)[-3:][::-1]top_features = [X.columns[idx] for idx in top_features_idx]for i, feature_idx in enumerate(top_features_idx):feature_name = X.columns[feature_idx]plt.figure(figsize=(10, 6))shap.dependence_plot(feature_idx,shap_values_sample,X_sample,feature_names=X.columns.tolist(),show=False)plt.title(f'SHAP Dependence Plot - {feature_name}', fontsize=14, pad=20)plt.tight_layout()plt.savefig(f'shap_dependence_plot_feature_{i + 1}_{feature_name}.png',dpi=300, bbox_inches='tight')print(f"已保存: shap_dependence_plot_feature_{i + 1}_{feature_name}.png")plt.close()# 5. Force Plot (针对第一个测试样本 - 保存为图片)print("\n生成 SHAP Force Plot (第一个测试样本)...")# 对于单个样本的force plotshap.force_plot(explainer.expected_value,shap_values_test[0],X_test_scaled_full[0],feature_names=X.columns.tolist(),matplotlib=True,show=False)plt.title('SHAP Force Plot - 第一个测试样本', fontsize=14, pad=20)plt.tight_layout()plt.savefig('shap_force_plot_sample1.png', dpi=300, bbox_inches='tight')print("已保存: shap_force_plot_sample1.png")plt.close()# 6. SHAP Values Heatmap (测试集所有样本)print("\n生成 SHAP Values Heatmap...")plt.figure(figsize=(14, 8))# 按SHAP值的绝对值排序特征feature_order = np.argsort(np.abs(shap_values_test).mean(axis=0))[::-1]# 创建热图shap_values_sorted = shap_values_test[:, feature_order]feature_names_sorted = [X.columns[i] for i in feature_order]plt.imshow(shap_values_sorted.T, aspect='auto', cmap='RdBu_r',interpolation='nearest')plt.colorbar(label='SHAP值')plt.yticks(range(len(feature_names_sorted)), feature_names_sorted)plt.xlabel('测试样本索引', fontsize=12)plt.ylabel('特征', fontsize=12)plt.title('SHAP Values Heatmap - 测试集所有样本', fontsize=14, pad=20)plt.tight_layout()plt.savefig('shap_heatmap.png', dpi=300, bbox_inches='tight')print("已保存: shap_heatmap.png")plt.close()# ==================== PDP 分析 ====================print("\n" + "-" * 70)print("2. 生成 Partial Dependence Plots (PDP)...")print("-" * 70)# 获取前6个最重要的特征top_6_features_idx = np.argsort(feature_importance)[-6:][::-1]top_6_features = [X.columns[idx] for idx in top_6_features_idx]print(f"生成前6个重要特征的PDP图: {top_6_features}")# 单特征PDP图 (2x3网格)fig, axes = plt.subplots(2, 3, figsize=(18, 12))axes = axes.ravel()for i, feature_idx in enumerate(top_6_features_idx):feature_name = X.columns[feature_idx]display = PartialDependenceDisplay.from_estimator(model_for_shap,X_train_val_scaled,[feature_idx],feature_names=X.columns.tolist(),ax=axes[i],grid_resolution=50)axes[i].set_title(f'PDP - {feature_name}', fontsize=12)plt.suptitle('Partial Dependence Plots - 前6个重要特征', fontsize=16, y=1.02)plt.tight_layout()plt.savefig('pdp_top6_features.png', dpi=300, bbox_inches='tight')print("已保存: pdp_top6_features.png")plt.close()# 生成单个特征的详细PDP图print("\n生成单个特征的详细PDP图...")for i, feature_idx in enumerate(top_6_features_idx[:3]):  # 只为前3个特征生成详细图feature_name = X.columns[feature_idx]fig, ax = plt.subplots(figsize=(10, 6))display = PartialDependenceDisplay.from_estimator(model_for_shap,X_train_val_scaled,[feature_idx],feature_names=X.columns.tolist(),ax=ax,grid_resolution=100)ax.set_title(f'Partial Dependence Plot - {feature_name}', fontsize=14)ax.set_xlabel(feature_name, fontsize=12)ax.set_ylabel('部分依赖', fontsize=12)plt.tight_layout()plt.savefig(f'pdp_detailed_feature_{i + 1}_{feature_name}.png',dpi=300, bbox_inches='tight')print(f"已保存: pdp_detailed_feature_{i + 1}_{feature_name}.png")plt.close()# 2D PDP (特征交互图) - 选择前2个最重要的特征print("\n生成 2D PDP (特征交互图)...")if len(top_6_features_idx) >= 2:feature_pairs = [(top_6_features_idx[0], top_6_features_idx[1]),(top_6_features_idx[0], top_6_features_idx[2]) if len(top_6_features_idx) > 2 else None,]for pair_idx, pair in enumerate(feature_pairs):if pair is None:continuefeature1_name = X.columns[pair[0]]feature2_name = X.columns[pair[1]]fig, ax = plt.subplots(figsize=(10, 8))display = PartialDependenceDisplay.from_estimator(model_for_shap,X_train_val_scaled,[pair],feature_names=X.columns.tolist(),ax=ax,grid_resolution=30)ax.set_title(f'2D PDP - {feature1_name} vs {feature2_name}', fontsize=14)plt.tight_layout()plt.savefig(f'pdp_2d_interaction_{pair_idx + 1}.png',dpi=300, bbox_inches='tight')print(f"已保存: pdp_2d_interaction_{pair_idx + 1}.png")plt.close()# ==================== 输出特征重要性摘要 ====================print("\n" + "=" * 70)print("特征重要性摘要 (基于SHAP值)")print("=" * 70)# 创建特征重要性DataFramefeature_importance_df = pd.DataFrame({'特征': X.columns,'SHAP重要性': feature_importance,'RF特征重要性': model_for_shap.feature_importances_})feature_importance_df = feature_importance_df.sort_values('SHAP重要性', ascending=False)print("\n前10个最重要的特征:")print(feature_importance_df.head(10).to_string(index=False))# 保存特征重要性feature_importance_df.to_csv('feature_importance_analysis.csv',index=False, encoding='utf-8-sig')print("\n特征重要性已保存至 'feature_importance_analysis.csv'")print("\n" + "=" * 70)print("SHAP 和 PDP 分析完成！")print("=" * 70)print("\n生成的图片文件:")print("  - shap_summary_plot.png (SHAP汇总图-蜂群图)")print("  - shap_feature_importance.png (特征重要性条形图)")print("  - shap_waterfall_plot_sample1.png (瀑布图-样本1)")print("  - shap_dependence_plot_feature_*.png (依赖图)")print("  - shap_force_plot_sample1.png (力图-样本1)")print("  - shap_heatmap.png (SHAP值热图)")print("  - pdp_top6_features.png (PDP-前6特征)")print("  - pdp_detailed_feature_*.png (详细PDP图)")print("  - pdp_2d_interaction_*.png (2D特征交互图)")except ImportError as e:print(f"\n错误: 缺少必要的库: {e}")print("请安装: pip install shap")
except Exception as e:print(f"\n分析过程中出现错误: {e}")import tracebacktraceback.print_exc()