命题逻辑基础，形式系统，定理证明（二）

一.命题逻辑运算

1.一元运算¬：取反

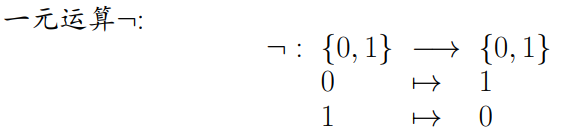
2.二元运算∧：全1则1

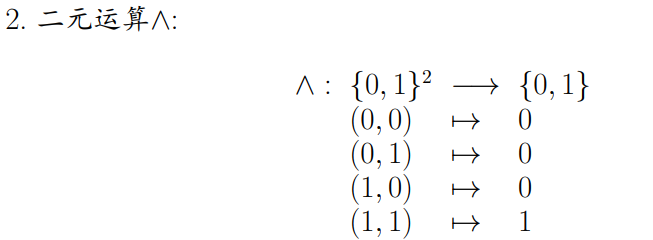
3.二元运算∨：全0则0

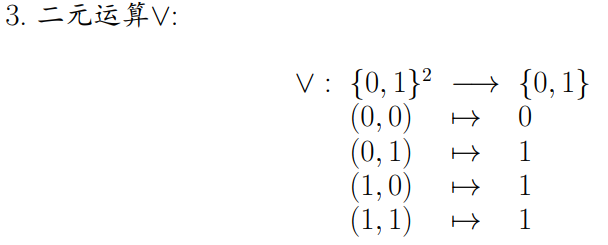
4.二元运算→ ：大推小为0，否则为1

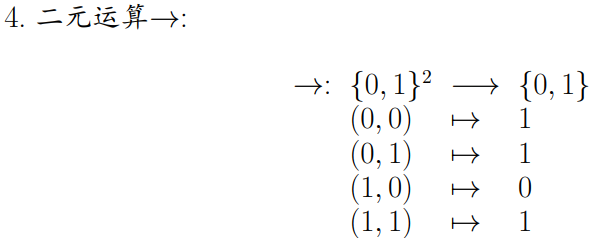
二.析取、合取范式

1.定义

合取范式（Conjunctive Normal Form, CNF）和析取范式（Disjunctive Normal Form, DNF）是逻辑学中用于描述命题逻辑表达式的两种标准形式。

合取范式是指一个逻辑表达式由多个析取子句通过逻辑与（∧）连接而成，例： (A∨B)∧(C∨D)。

析取范式是指一个逻辑表达式由多个合取子句通过逻辑或（∨）连接而成，例： (A∧B)∨(¬A∧C)。

每个命题公式都存在与之等值的合取范式和析取范式，并且它们的形式是唯一的。

最后这个定理表明，析取范式是一个永真式（1），在求取过程中，列出真值表，将最后真值为1的式子全部使用逻辑或（∨）连接起来。合取范式是一个矛盾式（0），在求取过程中，列出真值表，将最后真值为0的式子全部使用逻辑与（∧）连接起来。

2.重言式、矛盾式

简而言之，对于某式子，无论式子中各个命题变元取什么值，式子恒为1，则说明该式子为重言式（永真）。无论式子中各个命题变元取什么值，式子恒为0，则说明该式子为矛盾式（永假）。一般来说，某式子对于命题变元取不同的值，会有不同的结果，或真（1），或假（0）。

给个重言式的证明：

3.求取范式，运用逻辑运算

分析：在本式子中，列出真值表，合取范式是将所有为0的式子进行逻辑与（∧），每个式子由各个命题变元或命题变元的非运算用或运算（∨）连接起来的；析取范式是将所有为1的式子进行逻辑或（∨），每个式子由各个命题变元或命题变元的非运算用与运算（∧）连接起来的。

三.逻辑等价、真值等价

1.概念

这个地方主要是将或运算，与运算和蕴含（→）串联起来进行运算，原理是命题变元取一样的值，最后运算的结果一致。比如在求取某式子的析取合取范式时，将式子中出现的蕴含符号消去，运算后化成范式的标准形式。 在运算过程中可以使用离散数学中的一些定理简化运算。

可以使用上式子去除蕴含符号。

2.求取析取、合取范式

这个图是在浏览器中搜到的，足以展示。

四.真度

1.概念

~假设式子A含有n个命题变元，则A的赋值有2^n个。

~对图片中真度，换一种方式解释，列出某式A的真值表，选出值为1的，称之为真，作为真度的分子；A中若是有n个命题变元，则设置真度的分母为2^n。则像这样的分式就是该式子A的真度。