信道编码定理和信道编码逆定理

通信理论要解决的根本问题是如何快速、可靠地向目标传递信息，也就是通信系统的有效性和可靠性问题。

        通常用信息传输速率R来衡量通信的有效性，比特错误概率(Bit Error Rate, BER) 来衡量通信的可靠性。传统通信理论认为，二者是一对不可调和的矛盾，若想实现有扰信道下的无差错传输，唯一途径就是将信息传输速率降为零。

        这一传统的神话于1948 年被贝尔实验室的Claude E. Shannon 所击破。根据Shannon 的理论，一个典型的数字通信系统模型如下图所示。

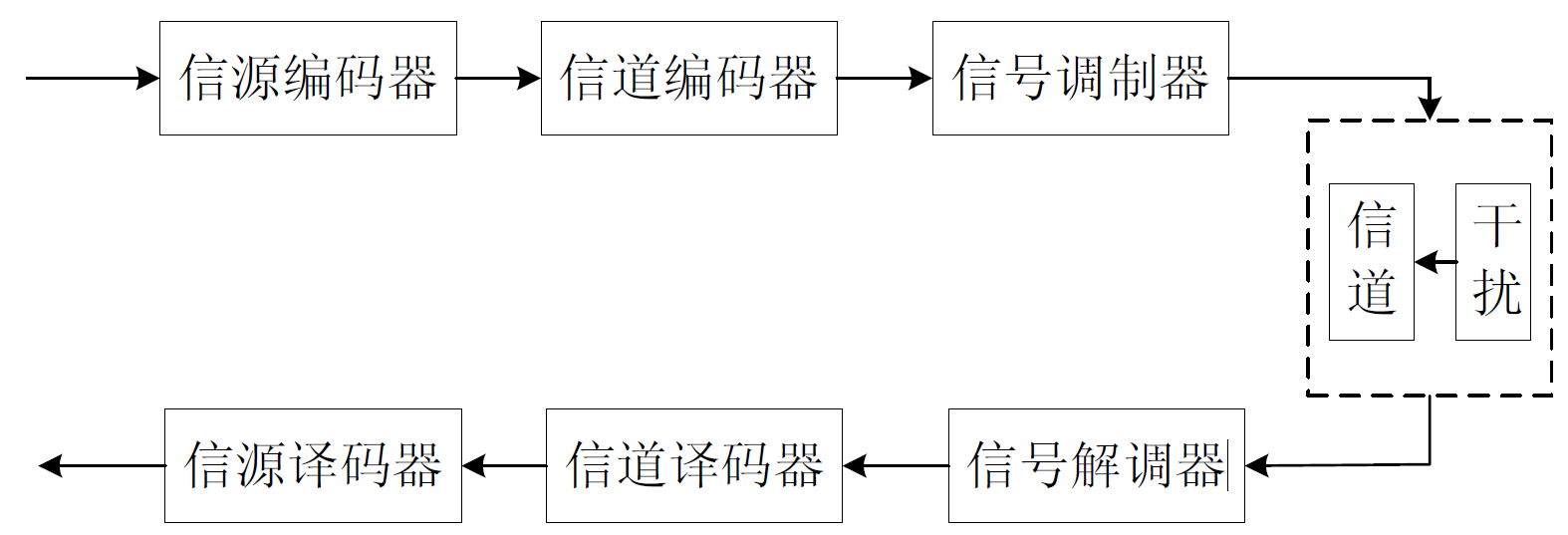
在数字通信系统中，噪声干扰是影响通信性能的根本因素，但是通过构建好的信道来改善通信需要花费高昂的代价，使用信道编码则更为经济和有效。

        Shannon 指出，任意离散输入无记忆平稳有噪声信道都存在信道容量C，它标志着信道传输能力的上限，只要信息传输速率R < C，就一定存在某种编码方式，当码长n足够大时，译码错误概率可以任意小；反之, 如果R > C，则无论采取何种编码方式也不能保证错误概率任意小。

        以上描述即为著名的信道编码定理和信道编码逆定理。