软考中级习题与解答——第十五章_数据结构与算法应用（2）

例题2

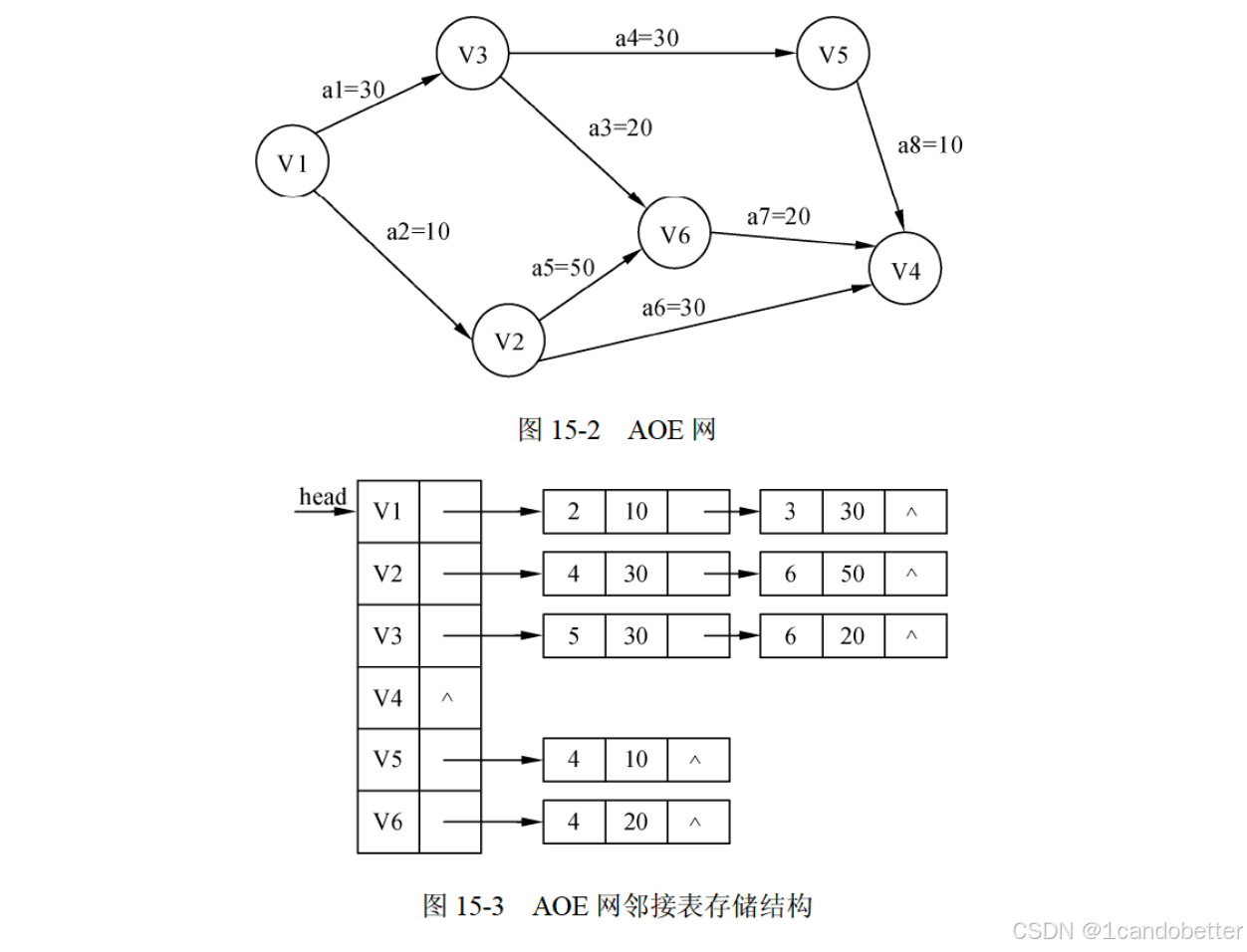
答案解析

(1) indegree[p->adjvex]++

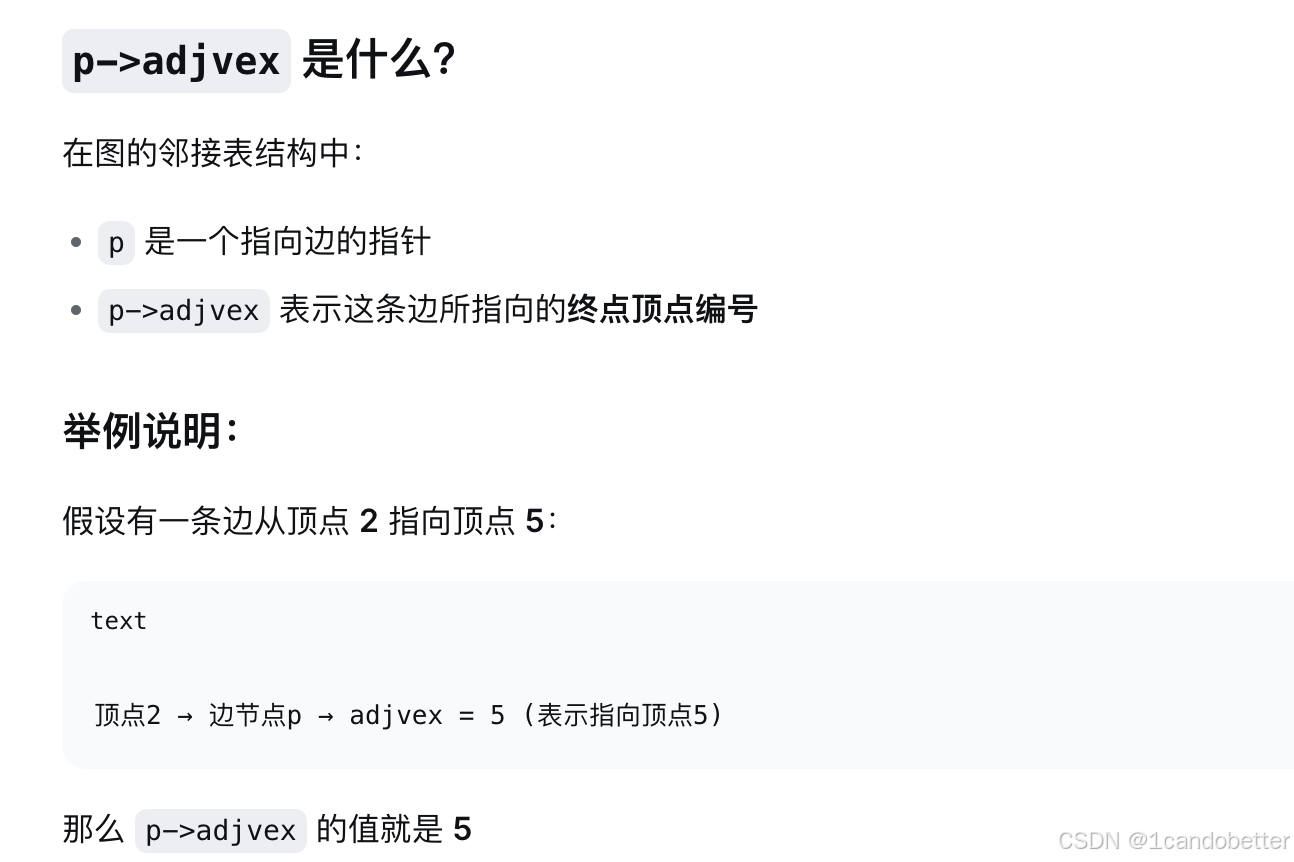
for( j = 1; j <= G.n; j++ ){      // 遍历图中的所有顶点p = G.head[j].Firstadj;       // 获取顶点 j 的第一个邻接边while(p ){                    // 当还有邻接边时循环___(1)__                  // 这里需要填写处理每条边的代码p = p->nextarc;           // 移动到下一个邻接边}
}

• G.n：图中顶点的总数

• G.head[j]：图中第 j 个顶点的头结点

• G.head[j].Firstadj：顶点 j 的第一条邻接边（边链表头指针）

• p：当前正在处理的边指针

• p->nextarc：当前边的下一条邻接边

(2) Stack[top--]

• 从栈中弹出栈顶元素

• top-- 表示先取栈顶元素，然后将栈顶指针下移

while(top > 0) {           // 当栈不为空时循环w = ___(2)__;          // 从栈中弹出一个顶点printf("%c", G.head[w].vdata);  // 输出该顶点p = G.head[w].Firstadj;         // 获取该顶点的第一条出边

(3) indegree[p->adjvex]--

• 减少顶点 p->adjvex 的入度

• 在拓扑排序中，当删除一个顶点时，需要减少其邻接点的入度

while(top > 0) {           // 当栈不为空时循环w = ___(2)__;          // 从栈中弹出一个顶点printf("%c", G.head[w].vdata);  // 输出该顶点p = G.head[w].Firstadj;         // 获取该顶点的第一条出边

(4) (ve[w]+p->weight) > ve[p->adjvex]

• 比较：从顶点 w 到 p->adjvex 的路径长度是否大于当前已知的最早开始时间

• 如果是，则更新 ve[p->adjvex] 的值

• 这是关键路径算法中求最早发生时间的关键步骤

    while(p) {                        // 遍历所有邻接点___(3)__;                     // 减少邻接点的入度if(!indegree[p->adjvex])      // 如果邻接点入度变为0Stack[++top] = p->adjvex; // 将该邻接点入栈if( ___(4)__ )                // 关键路径判断ve[p->adjvex] = ve[w] + p->weight;  // 更新最早开始时间p = p->nextarc;               // 处理下一条边}

(5) ve[w]