软考软件设计师常考知识点：（三）数据结构

一、线性结构

考点1：线性表

顺序表：数据在内存中紧邻。

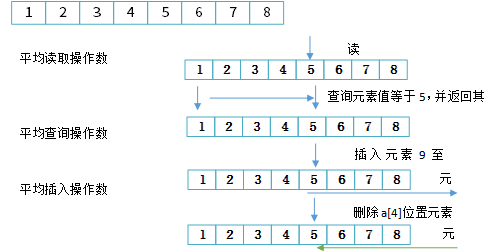
（1）顺序存储方式：数组的内存是连续分配的，并且是静态分配的，即在使用数组之前需要确定空间的大小，灵活性差。读数据快，其他操作效率慢。

a0

a1

a2

a3

a4

a5

a6

a7

（2）链表（linked-list）存储方式：链表的内存是不连续的。前一个元素紧邻的地址不一定是下一个元素。链表通过当前元素存储下个元素地址的方式把所有元素串起来。不需要连续空间，对内存友好。但是存储下个元素的地址，耗费更多空间。

特点：

①n个结点离散分布，彼此通过指针相联系。

②除头结点和尾结点外，每个结点只有一个前趋结点和一个后继结点。头结点没有前趋结点，尾结点没有后继结点。

③头结点并不存放有效数据，只存放链表首地址。其头结点的数据类型和首结点类型一样。

④加头结点的目的是方便对链表的操作，比如在链表头部进行结点的删除、插入。

【链表的分类】

单链表、循环链表、双向链表。

考点2：栈与队列

队列：先进先出

栈：先进后出

循环队列（通过整数取余运算实现）

队空条件：head=tail

队满条件：(tail+1)%size=head

队列长度：(tail-head+size)%size

循环队列的优点：

相比普通队列，此时入队和出队操作都不需要移动队列中的其他元素。

考点3：串

串的定义：串是仅由字符构成的有限序列，是一种线性表。一般记为S=‘a1a2a3…an’，其中，S是串名，单引号括起来的字符序列是串值。

串的存储

顺序存储；链式存储。

串的几个基本概念

（1）空串与空格串

空串：长度为零，不包含任何字符。

空格串：由一个或多个空格组成的串。虽然空格是一个空白字符，但它也是一个字符，在计算串长度时要将其计算在内。

（2）子串与子序列

子串：由串中任意长度的连续字符构成的序列称为子串。含有子串的串称为主串。子串在主串中的位置是指子串首次出现时，该子串的第一个字符在主串中的位置。空串是任意串的子串。

子序列：一个串的“子序列”（subsequence）是将这个串中的一些字符提取出来得到一个新串，并且不改变它们的相对位置关系。

（3）串比较与串相等

串比较：两个串比较大小时以字符的ASCII码值（或其他字符编码集合）作为依据。实质上，比较操作是从两个字符串的第一个字符开始进行，字符的码值大者所在的串为大；若其中一个串先结束，则以串长较大者为大。

串相等：指两个串长度相等且对应序号的字符也相同。

串的基本操作：

（1）赋值操作StrAssign(s,t)：将串s的值赋给串t。

（2）连接操作Concat(s,t)：将串t接续在串s的尾部，形成一个新的串。

（3）求串长StrLength(s)：返回串s的长度。

（4）串比较StrCompare(s,t)：比较两个串的大小。返回值-1、0和1分别表示s<t、s=t和s>t三种情况。

（5）求子串SubString(s,start,len)：返回串S中从start开始的、长度为len的字符序列。

二、数组与矩阵

数组

数组类型	存储地址计算
一维数组a[n]	a[i]的存储地址为：a+i*len
二维数组a[m][n]	a[i][j]的存储地址（按行存储）为：a+(i*n+j)*len a[i][j]的存储地址（按列存储）为：a+(j*m+i)*len

注：下标一般从0开始。

已知5行5列的二维数组a中的各元素占两个字节，求元素a[2][3]按行优先存储的存储地址？

间隔元素数量的计算口诀：

行标准，行标*总列数+列标，简称行列列。

列标准，列标*总行数+行标，简称列行行。

矩阵

稀疏矩阵	示意图	要点
上三角矩阵	上三角矩阵示意图	在矩阵中下标分别为i和j的元素，对应的一维数组的下标计算公式为： (2n-i+1) ´ i/2+j
下三角矩阵	下三角矩阵示意图	在矩阵中下标分别为i和j的元素，对应的一维数组的下标计算公式为： (i+1) ´

特殊矩阵	示意图	要点
对角矩阵	对角矩阵示意图	矩阵中的非零元素都集中在以主对角线为中心的对称带状区域中。

稀疏矩阵的表示形式：三元组表（行号，列号，元素值），例：（1,1,5），（1,2,10）等。

三、树

考点1：二叉树的存储与特性

1.树与二叉树的概念

结点（圆形）

分支（结点下面的线）

结点的度：该结点的子树数目

树的度：各结点度的最大值

叶子结点：度为0的结点-无分支

分支结点（非终端结点）：度不为0的结点-有分支

内部结点：除根以外的分支结点

层次：根为第1层，以此类推

树的高度：一棵树的最大层次数-总层数

父结点、子结点、兄弟结点

2.二叉树的定义

二叉树是n（n≥0）个结点的有限集合，它或者是空树（n=0），或者是由1个根结点及两棵不相交的且分别称为左、右子树的二叉树所构成。可见，二叉树同样具有递归性质

空树：没有结点的树。

单结点树：就只有一个顶点结点。

二叉树：所有结点的度不大于2的树。

满二叉树：任意结点，度为0或2（除最后一层以外，所有结点的度都为2）

软考更多备考学习资料

2025软考考试资料下载PDF版_软考历年真题打包下载版_免费视频课程下载_软考教材下载推荐_思维导图下载_考前冲刺备考资料_历年真题电子版网盘下载-希赛网https://wangxiao.xisaiwang.com/rk/xxzl/n101.html?fcode=h1000118_e3072