磁共振成像原理（理论）22：图像重建的常见问题 (General Issues of Image Reconstruction)

图像合成（或称重建）是断层成像的一个重要课题，主要原因在于空间信息是在数据采集过程中被编码到测量数据中的。根据空间信息被编码到测量数据中的方式不同，所需的图像重建技术可能会有显著差异。主要的编码方式有以下两种：

1. 笛卡尔采样​：从傅里叶变换样本进行图像重建，如下图左所示。
   • 数据点填充在由$k_x$和$k_y$轴构成的直角坐标系网格上。采样轨迹是平行于$k_x$轴或$k_y$轴的直线。在大多数序列中，这些线是逐行（或逐列）顺序填充的。
2. 径向采样​：从拉东变换样本进行图像重建，如下图右所示。
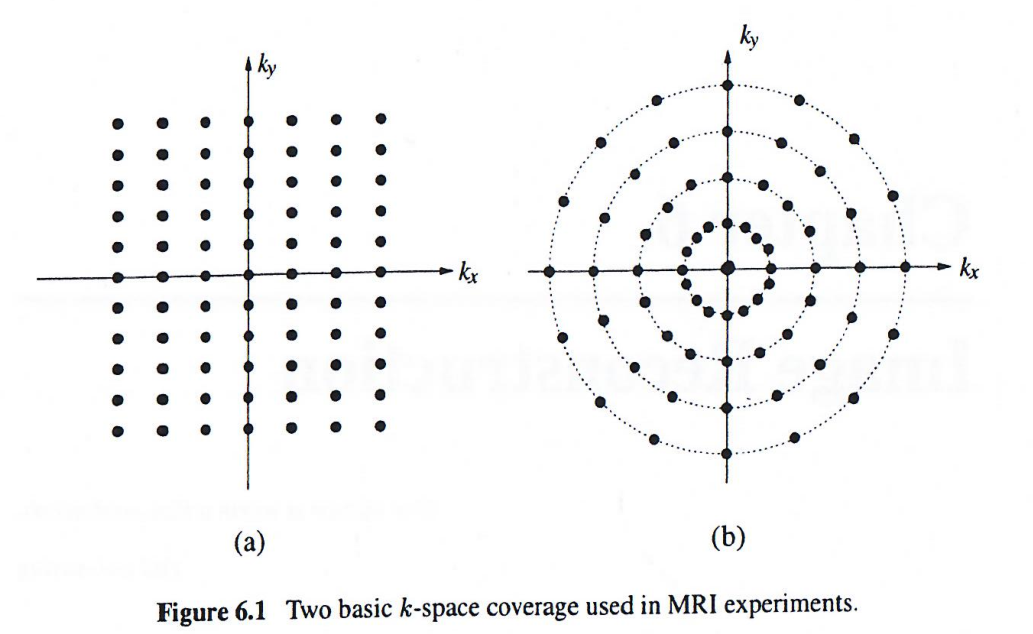
   • 数据采集沿着从K空间中心（原点）向外辐射的直线进行。这些径向线通常以固定的角度间隔旋转，从而覆盖整个K空间。图中所示的虚线包络线形象地表示了这种填充方式会形成一系列同心圆。
     

对于其他的$k$空间覆盖方式，通常采用信号插值技术将测量数据重新网格化到上述两种“标准”格式之一，以便应用基础的重建算法。

图像重建的常见问题

在磁共振成像中，图像重建问题的数学表述可以形式化地定义为：寻找一个图像函数 $I$，使其与测量信号 $S$ 满足已知的成像方程：

S=T{I}(6.1) S = \mathcal{T}\{I\} \tag{6.1} S=T{I}(6.1)

其中 $\mathcal{T}$ 通常是一个积分变换算子。在磁共振成像中，$\mathcal{T}$ 代表了各种空间信息编码方案。方程(6.1)通常被称为数据一致性约束，任何满足此约束的函数$\mathcal{T}$都被称为可行重建。

数据一致性约束的重要性在于，图像重建的本质是将测量数据中的信息转换为图像格式。违反数据一致性约束可能意味着这种转换步骤不忠实，可能导致有效信息的丢失或虚假信息的引入。

理论上，如果 $\mathcal{T}$ 是可逆的，则可以通过逆变换获得数据一致的图像函数：
I=T−1{S}(6.2) I = \mathcal{T}^{-1}\{S\} \tag{6.2} I=T−1{S}(6.2)

然而，在实际应用中，由于数据空间仅被部分采样，致使T−1{S}\mathcal{T}^{-1}\{S\}T−1{S} 无法直接计算。因此，图像重建的重点不是直接实现逆变换公式，而是通过逆变换的近似实现或其他方法，寻找满足数据一致性约束的图像函数。因此图像重建过程中涉及的一般性问题包括：

• 存在性
  • 给定一组测量数据，与数据一致的图像函数 $I$ 总是存在的，因为这些数据就是从物理对象产生的，这应该是不证自明的。
• 唯一性
  • 图像函数是否唯一取决于数据空间的采样方式。如果使用有限采样（实践中总是如此），对于给定的测量数据会存在多个可行的图像函数。而从众多“可行”的图像中选择一个，也是后续章节进一步要介绍的，这里先按下不表。
• 稳定性
  • 图像重建技术的稳定性涉及数据域中的扰动如何转化为可能的图像误差。这也是当下我们比较关心的：当梯度场存在非线性，接收机存在时序抖动时，这些负面影响最终都会转化为$k$空间数据的抖动，进而让重建出来的图像产生误差（比如说伪影）。

这里对稳定性简单展开介绍一下：具体来说，如果数据受到扰动 $\Delta S$，相应地图像函数产生误差 $\Delta I$，则有：
S+ΔS=T{I+ΔI}(6.3) S + \Delta S = \mathcal{T}\{I + \Delta I\} \tag{6.3} S+ΔS=T{I+ΔI}(6.3)

一个重要的问题是：对于小的 $\Delta S$，$\Delta I$ 是否也会很小？答案是：不一定。

以傅里叶成像为例，$\mathcal{T}$ 是傅里叶变换算子。根据著名的黎曼-勒贝格引理，我们可以向图像函数添加任意大幅度的分量，而不会显著扰动k空间数据。

假设一维物体的图像函数的误差为：
$$\Delta I=A\sin (2\pi k_{0}x)\text{\hspace{1em}(6.4)}$$
其中：

• $\Delta I$ 表示对原始图像 $I(x)$ 的扰动。
• $A$ 是正弦波的振幅，可以为任意大的常数。
• $k_0$ 是正弦波的空间频率，也可以为任意大的常数。
• $x$ 是空间坐标。

在傅里叶成像中，$k$空间数据 $S(k)$ 是图像 $I(x)$ 的傅里叶变换。因此，图像扰动 $\Delta I$ 导致的 $k$空间数据变化 $\Delta S(k)$ 为：

ΔS(k)=F{ΔI(x)}=∫−∞∞ΔI(x)e−i2πkxdx \Delta S(k) = \mathcal{F}\{\Delta I(x)\} = \int_{-\infty}^{\infty} \Delta I(x) e^{-i2\pi kx} dx ΔS(k)=F{ΔI(x)}=∫−∞∞​ΔI(x)e−i2πkxdx
当物体的实际尺寸被限制为$W_x$时，积分的上下限转化为 $[-W_x/2,W_x/2]$，即
$$\Delta S(k)={\int }_{-W_x/2}^{W_x/2}\Delta I(x)e^{-i2\pi kx}dx$$
将 $\Delta I=A\sin (2\pi k_{0}x)$ 代入上式：
$$\Delta S(k)={\int }_{-W_x/2}^{W_x/2}A\sin (2\pi k_{0}x)e^{-i2\pi kx}dx$$

利用欧拉公式 $\sin (\theta )=\frac{e^{i\theta }-e^{-i\theta }}{2i}$，将正弦函数展开：
$$\sin (2\pi k_{0}x)=\frac{e^{i2\pi k_{0}x}-e^{-i2\pi k_{0}x}}{2i}$$
代入积分式：
$$\Delta S(k)={\int }_{-W_x/2}^{W_x/2}A\left(\frac{e^{i2\pi k_{0}x}-e^{-i2\pi k_{0}x}}{2i}\right)e^{-i2\pi kx}dx$$
简化指数项：
$$\Delta S(k)=\frac{A}{2i}{\int }_{-W_x/2}^{W_x/2}\left[e^{i2\pi (k_0-k)x}-e^{-i2\pi (k_0+k)x}\right]dx$$

当 $k_0$ 趋近于无穷大时，被积函数 $e^{i2\pi (k_0-k)x}$ 和 $e^{-i2\pi (k_0+k)x}$ 成为高频振荡函数。根据黎曼-勒贝格引理，有限区间内的高频振荡函数的积分值趋近于零，可得：
$$\underset{k_0\to \infty }{\lim }\Delta S(k)=\underset{k_0\to \infty }{\lim }\frac{A}{2i}{\int }_{-W_x/2}^{W_x/2}\left[e^{i2\pi (k_0-k)x}-e^{-i2\pi (k_0+k)x}\right]dx=0$$

因此，得到公式 6.5：
$$\underset{k_0\to \infty }{\lim }\Delta S=\underset{k_0\to \infty }{\lim }{\int }_{-W_x/2}^{W_x/2}\Delta I(x)e^{-i2\pi kx}dx=0\text{\hspace{1em}(6.5)}$$

方程(6.4)和(6.5)表明，$\Delta S$ 可以变得可忽略不计，而 $\Delta I$ 却可以任意大。具有这种性质的算子被称为病态的。

由于大多数成像算子在本质上是病态的，并且由于有限采样而没有唯一解，重建问题被认为是一个病态问题。因此，从理论上讲，获得精确的真实图像函数是不可能的。

然而，如果我们"适当地"选择图像函数，可以在已知与真实图像函数偏差的情况下获得可接受的图像。如果成像过程是线性的，这种偏差可以通过点扩散函数完全表征，并且在某些情况下可以变得可忽略不计。