「机器学习笔记8」决策树学习：从理论到实践的全面解析（下）

本文将深入探讨决策树的高级话题，包括过拟合问题解决方案和实际应用中的扩展处理。

在上一篇文章中，我们介绍了决策树的基础概念和ID3算法原理。本文将继续深入探讨决策树学习中的过拟合问题、剪枝技术以及实际应用中的各种扩展处理方法。

一、决策树过拟合问题回顾

我们说h ∈H 对训练集过拟合，如果 存在另一个假设 h’ ∈H 满足：

$er{r}_{train}(h)<er{r}_{train}(h’)$ AND $er{r}_{train}(h)<er{r}_{train}(h’)$

过拟合是指模型在训练集上表现良好，但在未知数据上性能较差的现象。

决策树过拟合的一个极端例子:

• 每个叶节点都对应单个训练样本 —— 每个训练样本都被完美地分类
• 整棵树仅仅相当于一个数据查表实现

二、如何避免过拟合：剪枝技术

对决策树来说，有两种主要方法避免过拟合：

• 当数据的分裂在统计意义上并不显著时，就停止增长：预剪枝
• 构建一棵完全树，然后做后剪枝

1. 预剪枝：提前停止分裂

​基于样本数的停止条件​：当一个节点的训练样本数小于特定比例（如5%）时，不再继续分裂。这种方法避免了基于过少数据做出决策，减少了泛化误差。

​基于信息增益阈值的停止条件​：设定一个较小阈值，当信息增益低于该阈值时停止分裂。这种方法利用了所有训练数据，但阈值的设定需要经验。

2. 后剪枝：先构建后剪枝

后剪枝方法先构建一棵完全树，然后进行剪枝：

• ​验证集方法​：将数据集分为训练集和验证集，在验证集上测试剪去每个可能节点的影响，贪心地去掉能提升验证集准确率的节点

• ​MDL原则​：最小化描述长度，即 minimize(size(tree) + size(misclassifications(tree)))

3. 后剪枝: 错误降低剪枝

• 验证集
  • 已知标签
  • 测试效果
  • 在该集合上不做模型更新！
• 剪枝直到再剪就会对损害性能
  • 在验证集上测试剪去每个可能节点(和以其为根的子树)的影响
  • 贪心地去掉某个可以提升验证集准确率的节点

将节点剪去后，会出现新的叶子节点。如果定义新的叶节点的标签呢?

​叶节点标签赋值策略​：

• 赋值成最常见的类别

• 给这个节点多类别的标签

  • 每个类别有一个支持度 (根据训练集中每种标签的数目)
  • 测试时: 依据概率选择某个类别或选择多个标签

• 对于回归树（数值标签），可以做平均或加权平均

错误降低剪枝的效果

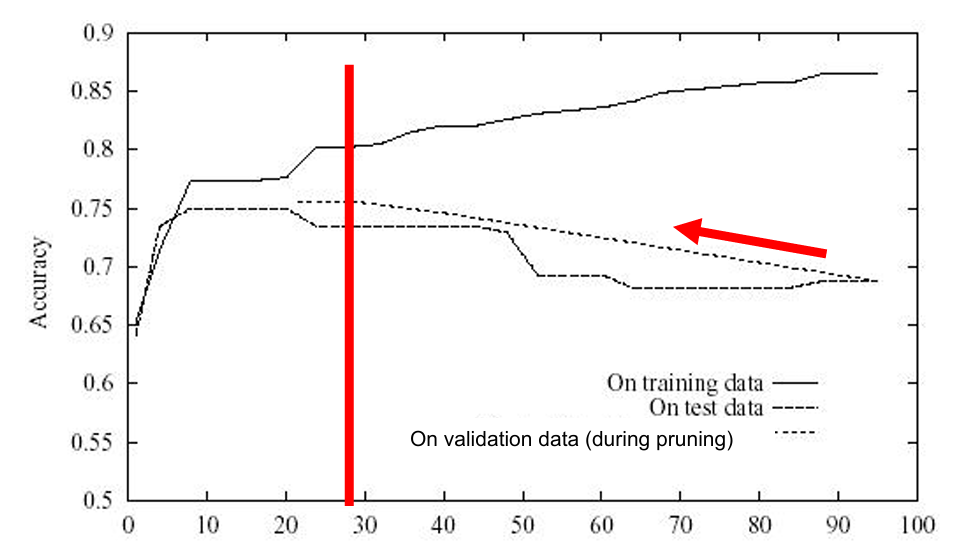
如上图，从后往前剪纸，一个个剪纸，让验证集性能进行提升，直到性能不再提升，结果大概是28个节点

4. 后剪枝：规则后剪枝

规则后剪枝是一种被广泛使用的方法（如C4.5算法），包含三个步骤：

1. ​规则转换​：将树转换成等价的规则集合

   • e.g. if (outlook=sunny)^(humidity=high) then playTennis = no

2. ​规则剪枝​：对每条规则去除能够提升准确率的规则前件

   • (outlook=sunny), (humidity=high)

3. ​规则排序​：将规则排序成一个序列 (根据规则的准确率从高往低排序)

4. 用该序列中的最终规则对样本进行分类（依次查看是否满足规则序列）

注：在规则被剪枝后，它可能不再能恢复成一棵树

为什么在剪枝前将决策树转化为规则?

• 1. 独立于上下文
  • 否则，如果子树被剪枝，有两个选择:
    • 完全删除该节点
    • 保留它
• 2. 不区分根节点和叶节点
• 3. 提升可读性

三、实际应用中的扩展处理

1. 连续属性值处理

温度	40	48	60	72	80	90
决策	No	No	Yes	Yes	Yes	No

决策树适合离散取值

实际应用中，我们需要将连续属性值离散化：

• ​选择阈值​：选择相邻但决策不同的值的中间值 $x_s=(x_l+x_u)/2$

• ​概率方法​：考虑概率 $x_s=(1-P)x_l+P{x}_u$

Fayyad在1991年证明了满足特定条件的阈值可以使信息增益最大化。

2. 具有过多取值的属性

问题:
• 偏差: 如果属性有很多值，根据信息增益IG，会优先被选择
• e.g. 享受运动的例子中，将一年里的每一天作为属性

• 一个可能的解决方法: 用 GainRatio （增益比）来替代

当属性有过多取值时，信息增益会偏向这些属性。解决方案是使用增益比​（GainRatio）替代信息增益：

$$GainRatio(S,A)=Gain(S,A)/SplitInformation(S,A)$$

其中SplitInformation是属性A上的熵，作为惩罚项。

3. 缺失属性值处理

处理缺失数据的常见方法：

• ​训练中最常见值​：选择该节点上训练样本中最常见的值

• ​相同标签中最常见值​：选择相同类别样本中最常见的值

• ​概率赋值​：根据概率分布进行赋值

以下面数据为例

BTR	Temp	…	label
neg	normal		-
neg	normal		-
neg	normal		-
neg	normal		-
neg	high		+
pos	normal		+
pos	high		+
pos	high		+
?	normal		+
训练中最常见值: 为neg
相同标签中最常见值: +对应的为pos
概率赋值: neg为5/8， pos为3/8

4. 有代价的属性

当某些属性收集代价较大时，可考虑代价敏感的决策树算法：

• Tan & Schlimmer (1990)

$$Gai{n}^2(S,A)/Cost(A)$$

• Nunez (1988)

$$\frac{2^{G}ain(S,A)-1}{(Cost(A)+1{)}^w}$$

w为代价因子，取值范围[0,1]

5. 其他信息

• 可能是最简单和频繁使用的算法

  • 易于理解
  • 易于实现
  • 易于使用
  • 计算开销小

• 决策森林

  • 由C4.5产生的许多决策树

实际应用

决策树在研究和应用中广泛使用：

• ​医疗诊断​：从临床症状推断疾病

• ​信用分析​：从个人信息判断客户价值

• ​日程规划​：自动化决策支持

决策树通常作为复杂算法的基准方法，也常被用作集成学习框架中的基础组件。

四、归纳学习假设

机器学习的核心是从已知样本中获得一般化概念。​归纳学习假设表明：任一假设若在足够大的训练样例集中很好地逼近目标函数，它也能在未见实例中很好地逼近目标函数。

这一假设是机器学习能够泛化的理论基础，但也需要注意过拟合问题，确保模型真正学习到了通用规律而非训练数据的特例。

---

决策树学习作为机器学习中最直观易懂的算法之一，不仅为初学者提供了理解机器学习概念的优秀途径，也在实际应用中发挥着重要作用。随着集成学习方法如随机森林和梯度提升决策树的发展，决策树的核心思想仍在继续推动着机器学习领域的进步。