《强化学习数学原理》学习笔记11——阶段策略迭代算法
前期知识:
1、值迭代算法;
2、策略迭代算法。
在强化学习的策略优化领域,价值迭代(Value Iteration)和策略迭代(Policy Iteration)是两种经典算法,但它们各有特点与局限。阶段策略迭代算法作为二者的“中间态”,巧妙融合优势,在计算效率与收敛速度间取得平衡。本文将深入剖析该算法。
一、价值迭代与策略迭代回顾
(一)策略迭代(Policy Iteration)
- 核心步骤(从 π0\pi_0π0 开始):
- 策略评估(Policy Evaluation, PE):给定策略 πk\pi_kπk,求解该策略下的状态价值 vπkv_{\pi_k}vπk,满足方程 vπk=rπk+γPπkvπkv_{\pi_k} = r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}vπk=rπk+γPπkvπk。
- 策略改进(Policy Improvement, PI):基于上一步得到的状态价值 vπkv_{\pi_k}vπk,求解更优策略 πk+1=argmaxπ(rπ+γPπvπk)\pi_{k + 1} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_{\pi_k})πk+1=argmaxπ(rπ+γPπvπk)。
- 特点:在策略评估阶段,求解状态价值 vπkv_{\pi_k}vπk 时也使用迭代求解的方式,相当于迭代算法中嵌套了一个迭代算法(理论上迭代了无限次),保证了价值的准确性,但计算成本高。
(二)价值迭代(Value Iteration)
- 核心步骤(从 v0v_0v0 开始):
- 策略更新(Policy Update, PU):给定当前状态价值vkv_kvk,求解策略πk+1=argmaxπ(rπ+γPπvk)\pi_{k + 1} = \arg\max_{\pi} (r_{\pi} + \gamma P_{\pi} v_k)πk+1=argmaxπ(rπ+γPπvk)。
- 价值更新(Value Update, VU):用新策略πk+1\pi_{k + 1}πk+1计算新状态价值vk+1=rπk+1+γPπk+1vkv_{k + 1} = r_{\pi_{k + 1}} + \gamma P_{\pi_{k + 1}} v_kvk+1=rπk+1+γPπk+1vk。
- 特点:策略更新时,状态价值 vkv_kvk 的计算在一次迭代中仅进行一步,计算高效,但因价值更新“粗糙”,收敛速度较慢。
二、阶段策略迭代的提出
上面两种算法的执行步骤如下所示:
策略迭代: π0⟶PEvπ0⟶PIπ1⟶PEvπ1⟶PIπ2⟶PEvπ2⟶PI…价值迭代: v0⟶PUπ1′⟶VUv1⟶PUπ2′⟶VUv2⟶PU…\begin{align*} \text{策略迭代: } &\pi_0 \stackrel{PE}{\longrightarrow} v_{\pi_0} \stackrel{PI}{\longrightarrow} \pi_1 \stackrel{PE}{\longrightarrow} v_{\pi_1} \stackrel{PI}{\longrightarrow} \pi_2 \stackrel{PE}{\longrightarrow} v_{\pi_2} \stackrel{PI}{\longrightarrow} \dots \\ \text{价值迭代: } &v_0 \stackrel{PU}{\longrightarrow} \pi_1' \stackrel{VU}{\longrightarrow} v_1 \stackrel{PU}{\longrightarrow} \pi_2' \stackrel{VU}{\longrightarrow} v_2 \stackrel{PU}{\longrightarrow} \dots \end{align*} 策略迭代: 价值迭代: π0⟶PEvπ0⟶PIπ1⟶PEvπ1⟶PIπ2⟶PEvπ2⟶PI…v0⟶PUπ1′⟶VUv1⟶PUπ2′⟶VUv2⟶PU…
通过对比价值迭代和策略迭代的执行步骤,发现二者流程相似,但在价值更新的深度上有差异:
| 步骤 | 策略迭代算法 | 价值迭代算法 | 说明 |
|---|---|---|---|
| 1)策略 | π0\pi_0π0 | 无 | - |
| 2)价值 | vπ0=rπ0+γPπ0vπ0v_{\pi_0} = r_{\pi_0} + \gamma P_{\pi_0} v_{\pi_0}vπ0=rπ0+γPπ0vπ0 | v0≐vπ0v_0 \doteq v_{\pi_0}v0≐vπ0 | - |
| 3)策略 | π1=argmaxπ(rπ+γPπvπ0)\pi_1 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{\pi_0})π1=argmaxπ(rπ+γPπvπ0) | π1=argmaxπ(rπ+γPπv0)\pi_1 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_0)π1=argmaxπ(rπ+γPπv0) | 两种策略相同 |
| 4)价值 | vπ1=rπ1+γPπ1vπ1v_{\pi_1} = r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}vπ1=rπ1+γPπ1vπ1 | v1=rπ1+γPπ1v0v_1 = r_{\pi_1} + \gamma P_{\pi_1} v_0v1=rπ1+γPπ1v0 | vπ1≥v1v_{\pi_1} \geq v_1vπ1≥v1,因vπ1≥vπ0v_{\pi_1} \geq v_{\pi_0}vπ1≥vπ0 |
| 3)策略 | π2=argmaxπ(rπ+γPπvπ0)\pi_2 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{\pi_0})π2=argmaxπ(rπ+γPπvπ0) | π2=argmaxπ(rπ+γPπv1)\pi_2 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_1)π2=argmaxπ(rπ+γPπv1) | - |
价值迭代在第四步仅做一步价值更新(v1=rπ1+γPπ1v0v_1 = r_{\pi_1} + \gamma P_{\pi_1} v_0v1=rπ1+γPπ1v0),而策略迭代要精确求解vπ1=rπ1+γPπ1vπ1v_{\pi_1} = r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}vπ1=rπ1+γPπ1vπ1(理论上需无限次迭代)。若把策略迭代中策略评估的迭代次数限制为有限次,就得到了阶段策略迭代。
三、阶段策略迭代算法
(一)算法流程
阶段策略迭代与策略迭代类似,只是在策略评估步骤仅执行有限次迭代(记为jtruncatej_{\text{truncate}}jtruncate)。具体步骤如下:
- 初始化:已知所有(s,a)(s, a)(s,a)对应的概率模型p(r∣s,a)p(r|s, a)p(r∣s,a)和p(s′∣s,a)p(s'|s, a)p(s′∣s,a),设定初始策略π0\pi_0π0。
- 策略评估:
- 初始化:选择vk(0)=vk−1v_k^{(0)} = v_{k - 1}vk(0)=vk−1作为初始猜测,设置最大迭代次数jtruncatej_{\text{truncate}}jtruncate。
- 迭代更新:对于每个状态s∈Ss \in \mathcal{S}s∈S,执行vk(j+1)(s)=∑aπk(a∣s)[∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(j)(s′)]v_k^{(j + 1)}(s) = \sum_a \pi_k(a|s) \left[ \sum_r p(r|s, a)r + \gamma \sum_{s'} p(s'|s, a)v_k^{(j)}(s') \right]vk(j+1)(s)=∑aπk(a∣s)[∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(j)(s′)],直到迭代次数达到jtruncatej_{\text{truncate}}jtruncate,然后令vk=vk(jtruncate)v_k = v_k^{(j_{\text{truncate}})}vk=vk(jtruncate)。
- 策略改进:
- 对每个状态s∈Ss \in \mathcal{S}s∈S和动作a∈A(s)a \in \mathcal{A}(s)a∈A(s),计算qk(s,a)=∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′)q_k(s, a) = \sum_r p(r|s, a)r + \gamma \sum_{s'} p(s'|s, a)v_k(s')qk(s,a)=∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vk(s′)。
- 找到使qk(s,a)q_k(s, a)qk(s,a)最大的动作a∗(s)=argmaxaqk(s,a)a^*(s) = \arg\max_a q_k(s, a)a∗(s)=argmaxaqk(s,a),更新策略πk+1(a∣s)=1\pi_{k + 1}(a|s) = 1πk+1(a∣s)=1(若a=ak∗a = a^*_ka=ak∗),否则πk+1(a∣s)=0\pi_{k + 1}(a|s) = 0πk+1(a∣s)=0。
- 收敛判断:若vkv_kvk未收敛,重复上述步骤;否则停止,得到最优状态价值和最优策略。
(二)算法特点
- 与价值迭代、策略迭代的关系:
- 当jtruncate=1j_{\text{truncate}} = 1jtruncate=1时,阶段策略迭代退化为价值迭代,因为策略评估仅做一步更新。
- 当jtruncate→∞j_{\text{truncate}} \to \inftyjtruncate→∞时,阶段策略迭代退化为策略迭代,因为策略评估要精确求解。
- 优势:
- 相较于策略迭代,阶段策略迭代在策略评估步骤只需有限次迭代,计算效率更高。
- 相较于价值迭代,阶段策略迭代通过在策略评估步骤多进行几次迭代,能加快收敛速度。
四、收敛性分析
(一)价值改进性质
考虑策略评估步骤的迭代算法:vπk(j+1)=rπk+γPπkvπk(j),j=0,1,2,…v_{\pi_k}^{(j + 1)} = r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}^{(j)}, \ j = 0,1,2,\dotsvπk(j+1)=rπk+γPπkvπk(j), j=0,1,2,…。若初始猜测vπk(0)=vπk−1v_{\pi_k}^{(0)} = v_{\pi_{k - 1}}vπk(0)=vπk−1,则有vπk(j+1)≥vπk(j)v_{\pi_k}^{(j + 1)} \geq v_{\pi_k}^{(j)}vπk(j+1)≥vπk(j)对j=0,1,2,…j = 0,1,2,\dotsj=0,1,2,…成立。
(二)证明(简要)
- 由迭代公式可得vπk(j+1)−vπk(j)=γPπk(vπk(j)−vπk(j−1))=⋯=γjPπkj(vπk(1)−vπk(0))v_{\pi_k}^{(j + 1)} - v_{\pi_k}^{(j)} = \gamma P_{\pi_k} (v_{\pi_k}^{(j)} - v_{\pi_k}^{(j - 1)}) = \dots = \gamma^j P_{\pi_k}^j (v_{\pi_k}^{(1)} - v_{\pi_k}^{(0)})vπk(j+1)−vπk(j)=γPπk(vπk(j)−vπk(j−1))=⋯=γjPπkj(vπk(1)−vπk(0))。
- 因为vπk(0)=vπk−1v_{\pi_k}^{(0)} = v_{\pi_{k - 1}}vπk(0)=vπk−1,且πk=argmaxπ(rπ+γPπvπk−1)\pi_k = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{\pi_{k - 1}})πk=argmaxπ(rπ+γPπvπk−1),所以vπk(1)=rπk+γPπkvπk−1≥rπk−1+γPπk−1vπk−1=vπk−1=vπk(0)v_{\pi_k}^{(1)} = r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_{k - 1}} \geq r_{\pi_{k - 1}} + \gamma P_{\pi_{k - 1}} v_{\pi_{k - 1}} = v_{\pi_{k - 1}} = v_{\pi_k}^{(0)}vπk(1)=rπk+γPπkvπk−1≥rπk−1+γPπk−1vπk−1=vπk−1=vπk(0)。
- 代入上式可推出vπk(j+1)≥vπk(j)v_{\pi_k}^{(j + 1)} \geq v_{\pi_k}^{(j)}vπk(j+1)≥vπk(j)。
尽管实际中vπk−1v_{\pi_{k - 1}}vπk−1不可直接获取,只有vk−1v_{k - 1}vk−1可用,但该性质仍为阶段策略迭代的收敛性提供了理论支撑。
五、总结
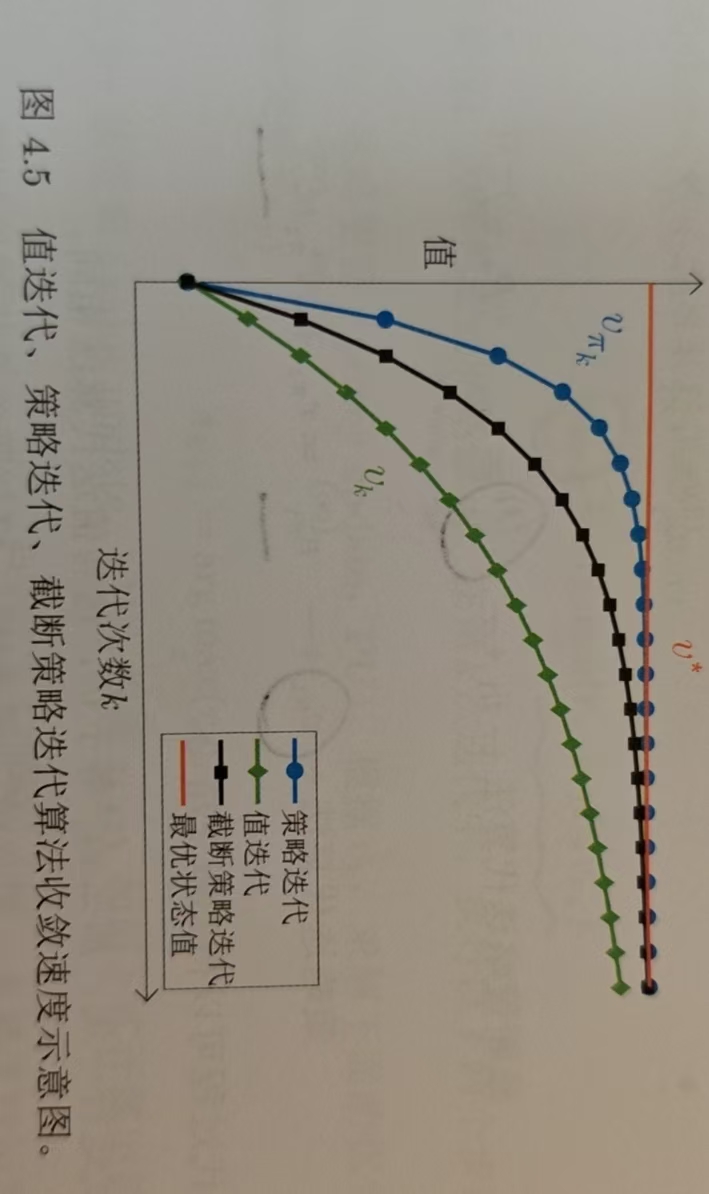
阶段策略迭代算法是强化学习中一种灵活的策略优化方法,它处于价值迭代和策略迭代之间,既避免了策略迭代中策略评估的高计算成本,又弥补了价值迭代收敛速度慢的不足,在计算效率与收敛速度间取得了良好平衡,为解决强化学习中的策略优化问题提供了更高效的途径。三种算法的收敛速度对比示意图如下: