当前位置：首页 > news >正文

leetcode排序链表

news 2025/10/9 7:00:32

自用

1.归并排序

归并排序（Merge Sort）是一种经典的分治算法，用于将一组数据按照指定顺序（通常是升序或降序）进行排序。它的核心思想是将一个大问题分解成若干个小问题，分别解决这些小问题，然后将结果合并起来，从而得到最终的解决方案。以下是归并排序的详细步骤：

分解（Divide）

步骤描述：将待排序的数组从中间位置分成两个大致相等的子数组。如果数组长度为偶数，则两个子数组长度相等；如果数组长度为奇数，则一个子数组比另一个子数组多一个元素。
举例：对于数组 [8, 4, 23, 42, 16, 15]，分解后得到两个子数组 [8, 4, 23] 和 [42, 16, 15]。

解决（Conquer）

步骤描述：递归地对这两个子数组进行归并排序。递归的基本情况是当子数组的长度为1或0时，认为它已经有序，不需要进一步分解。
举例：对子数组 [8, 4, 23] 进行归并排序，首先将其分解为 [8] 和 [4, 23]。[8] 已经有序，对 [4, 23] 进行归并排序，分解为 [4] 和 [23]，这两个子数组都有序，然后合并它们得到 [4, 23]。最后将 [8] 和 [4, 23] 合并得到 [4, 8, 23]。

合并（Combine）

步骤描述：将两个已经排序的子数组合并成一个有序的数组。合并过程中，比较两个子数组的元素，将较小的元素依次放入新的数组中，直到所有元素都被合并。
举例：合并 [4, 8, 23] 和 [15, 16, 42]，首先比较 4 和 15，将 4 放入新数组；然后比较 8 和 15，将 8 放入；接着比较 23 和 15，将 15 放入；依此类推，最终得到 [4, 8, 15, 16, 23, 42]。

性能分析

时间复杂度：归并排序的时间复杂度为 O(n log n)，其中 n 是数组的长度。
这是因为每次分解都将问题规模减半->logn
而合并操作需要线性时间->n
空间复杂度：归并排序需要额外的存储空间来合并子数组，因此其空间复杂度为 O(n)。

稳定性

稳定性：归并排序是一种 稳定排序算法。在合并过程中，如果两个元素相等，会先放入来自左侧子数组的元素，从而保持它们的相对顺序。

2.链表+归并

1.排序合并

归并的核心就是拆解排序再合并

假如有两个有序链表该如何合并，这个比较简单，使用双指针即可

参考题目：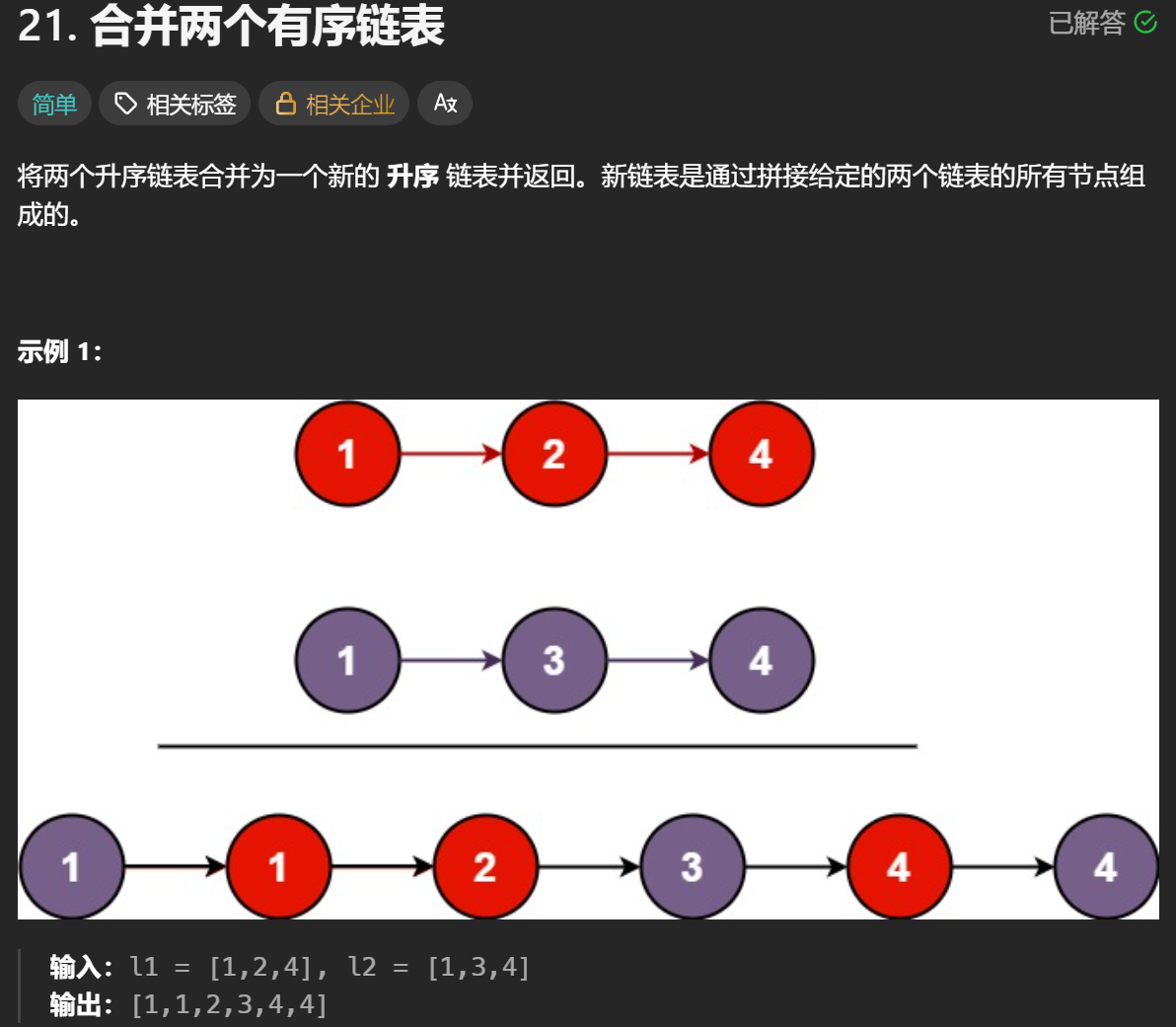

https://leetcode.cn/problems/merge-two-sorted-lists

用两个指针分别指向两个链表的开头，比较两个指针指向的数的大小，选择小的，再把这个指针向前移动一步就行

class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {ListNode* preHead = new ListNode(-1);ListNode* prev = preHead;while (l1 != nullptr && l2 != nullptr) {if (l1->val < l2->val) {prev->next = l1;l1 = l1->next;} else {prev->next = l2;l2 = l2->next;}prev = prev->next;}// 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可prev->next = l1 == nullptr ? l2 : l1;return preHead->next;}
};

2.拆分

每次都从中间拆分，如何找到中间的位置，这里使用快慢指针处理

快指针的速度是慢指针速度的两倍，使得快指针到达末尾时慢指针到一半的位置

ListNode* sortList(ListNode* head, ListNode* tail) {if (head == nullptr) {return head;}if (head->next == tail) {head->next = nullptr;return head;}//特殊判断ListNode* slow = head, *fast = head;while (fast != tail) {slow = slow->next;fast = fast->next;if (fast != tail) {fast = fast->next;}}//快慢指针找到头尾ListNode* mid = slow;return merge(sortList(head, mid), sortList(mid, tail));
//递归调用}

相当于就是对于每一个链表，只要链表元素在2个及以上就可以拆成两个部分放入排序

力扣参考答案：

class Solution {
public:ListNode* sortList(ListNode* head) {return sortList(head, nullptr);}ListNode* sortList(ListNode* head, ListNode* tail) {if (head == nullptr) {return head;}if (head->next == tail) {head->next = nullptr;return head;}ListNode* slow = head, *fast = head;while (fast != tail) {slow = slow->next;fast = fast->next;if (fast != tail) {fast = fast->next;}}ListNode* mid = slow;return merge(sortList(head, mid), sortList(mid, tail));}ListNode* merge(ListNode* head1, ListNode* head2) {ListNode* dummyHead = new ListNode(0);ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;while (temp1 != nullptr && temp2 != nullptr) {if (temp1->val <= temp2->val) {temp->next = temp1;temp1 = temp1->next;} else {temp->next = temp2;temp2 = temp2->next;}temp = temp->next;}if (temp1 != nullptr) {temp->next = temp1;} else if (temp2 != nullptr) {temp->next = temp2;}return dummyHead->next;}
};作者：力扣官方题解
链接：https://leetcode.cn/problems/sort-list/solutions/492301/pai-xu-lian-biao-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3.非递归解法

非递归解法就是基于最开始的分治思想，

从长度1开始对两段链表排序，

然后是长度2的两段链表排序，

直到链表长度超过了总长度的一半，

现在只需要对超过总长度一半的链表和剩下的一段链表排序即可

边界处理比较复杂但是当每一个小段长度是1的时候最容易理解代码

class Solution {
public:ListNode* sortList(ListNode* head) {if (head == nullptr) {return head;}//特判int length = 0;ListNode* node = head;while (node != nullptr) {length++;node = node->next;}//计算长度ListNode* dummyHead = new ListNode(0, head);//设置哨兵for (int subLength = 1; subLength < length; subLength <<= 1) {ListNode* prev = dummyHead, *curr = dummyHead->next;while (curr != nullptr) {ListNode* head1 = curr;for (int i = 1; i < subLength && curr->next != nullptr; i++) {curr = curr->next;}ListNode* head2 = curr->next;curr->next = nullptr;curr = head2;for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {curr = curr->next;}ListNode* next = nullptr;if (curr != nullptr) {next = curr->next;curr->next = nullptr;}ListNode* merged = merge(head1, head2);prev->next = merged;while (prev->next != nullptr) {prev = prev->next;}curr = next;}}return dummyHead->next;}ListNode* merge(ListNode* head1, ListNode* head2) {ListNode* dummyHead = new ListNode(0);ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;while (temp1 != nullptr && temp2 != nullptr) {if (temp1->val <= temp2->val) {temp->next = temp1;temp1 = temp1->next;} else {temp->next = temp2;temp2 = temp2->next;}temp = temp->next;}if (temp1 != nullptr) {temp->next = temp1;} else if (temp2 != nullptr) {temp->next = temp2;}return dummyHead->next;}
};作者：力扣官方题解
链接：https://leetcode.cn/problems/sort-list/solutions/492301/pai-xu-lian-biao-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

4.拓展

最直观的方法就是先把所有链表合在一起然后用归并排序处理，但是由于一开始链表就是有序的所以可以利用一下最初有序的条件

这里的标准方法叫做优先队列合并

优先队列

优先队列（Priority Queue） 是一种特殊的队列数据结构，其特点是：

元素按优先级排序：出队顺序由元素的优先级决定，而非入队顺序。
优先级高的元素先出队：每次取出的元素都是当前队列中优先级最高的。

class Solution {
public:struct Status {int val;ListNode *ptr;bool operator < (const Status &rhs) const {return val > rhs.val;}};priority_queue <Status> q;ListNode* mergeKLists(vector<ListNode*>& lists) {for (auto node: lists) {if (node) q.push({node->val, node});}ListNode head, *tail = &head;while (!q.empty()) {auto f = q.top(); q.pop();tail->next = f.ptr; tail = tail->next;if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});}return head.next;}
};作者：力扣官方题解
链接：https://leetcode.cn/problems/merge-k-sorted-lists/solutions/219756/he-bing-kge-pai-xu-lian-biao-by-leetcode-solutio-2/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

结构体 Status

struct Status {int val;          // 当前节点的值ListNode *ptr;    // 当前节点的指针bool operator<(const Status &rhs) const {return val > rhs.val;   // 注意：这是“小根堆”}
};

把链表节点包装成一个可比较的小对象。
重载 < 时反过来写（val > rhs.val），使得 priority_queue 内部 值小的在堆顶，形成 小根堆（模拟最小优先队列）。
bool
返回值类型：这个函数最后只回答“是/否”（true / false）。
operator<
函数名字：它重载了“小于号 <”。
以后写 a < b 时，编译器实际会调用这个函数。
(const Status &rhs) const
参数列表：
- rhs 是“右操作数”，即 a < b 里的 b。
- 前面加 const 并传引用，保证只读且不开销拷贝。
- 末尾的 const 告诉编译器“函数体内**绝不修改当前对象（左操作数 a）的任何成员”。
return val > rhs.val;
函数体：
- 当当前对象的 val 大于 rhs 的 val 时返回 true。
- 效果就是把“更小”的 rhs 判成“排在前面”，从而把小元素推向堆顶。
整体作用
让标准库的大根堆 priority_queue 误以为“小值更大”，于是堆顶变成最小值——小根堆就这么骗出来了。

优先队列定义

priority_queue<Status> q;

默认是 vector 做容器 + 堆算法。
由于上面 < 是反着写的，堆顶永远是 当前最小值。

初始化：把每条链表的头结点全部扔进堆

for (auto node: lists) {if (node) q.push({node->val, node});
}

过滤空链表。
每个 Status 记录头节点的值和指针。

虚拟头节点技巧

ListNode head, *tail = &head;

head 是栈上虚拟头，不存数据。
tail 始终指向结果链表的末尾，方便尾插。

主循环：每次取最小值接在结果后面

while (!q.empty()) {auto f = q.top(); q.pop();   // 取当前最小节点tail->next = f.ptr;          // 尾插tail = tail->next;           // 移动尾指针if (f.ptr->next)             // 如果该节点后面还有节点q.push({f.ptr->next->val, f.ptr->next});
}