530.二叉搜索树的最小绝对差（二叉树算法题）

530.二叉搜索树的最小绝对差

力扣题目链接

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

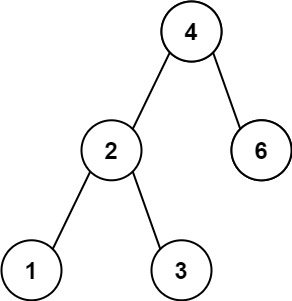
输入：root = [4,2,6,1,3]
输出：1

示例 2：

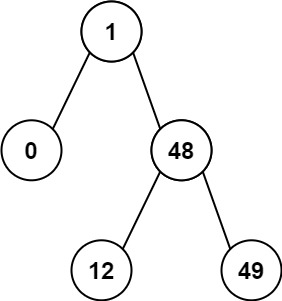
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

• 树中节点的数目范围是 [2, 104]
• 0 <= Node.val <= 105

算法公开课

《代码随想录》算法视频公开课 (opens new window)：二叉搜索树中，需要掌握如何双指针遍历！| LeetCode：530.二叉搜索树的最小绝对差 (opens new window)，相信结合视频再看本篇题解，更有助于大家对本题的理解。

#思路

题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。

注意是二叉搜索树，二叉搜索树可是有序的。

遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值，这样就简单多了。

#递归

那么二叉搜索树采用中序遍历，其实就是一个有序数组。

在一个有序数组上求两个数最小差值，这是不是就是一道送分题了。

最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/class Solution {// 用于存储中序遍历结果的列表// 因为是二叉搜索树（BST），中序遍历会得到一个升序序列private List<Integer> list;/*** 计算二叉搜索树中任意两个节点值之间的最小绝对差* 利用 BST 的性质：中序遍历得到升序序列，最小差值一定出现在相邻节点之间** @param root 二叉搜索树的根节点* @return 最小绝对差值*/public int getMinimumDifference(TreeNode root) {list = new ArrayList<>(); // 初始化列表traversal(root);          // 执行中序遍历，将节点值按升序存入 listint result = Integer.MAX_VALUE; // 初始化结果为最大整数值// 遍历中序序列，比较每一对相邻元素的差值，取最小值for (int i = 1; i < list.size(); i++) {result = Math.min(result, list.get(i) - list.get(i - 1));}return result; // 返回最小差值}/*** 中序遍历二叉树（左 -> 根 -> 右）* 将节点值依次添加到 list 中，形成升序序列** @param root 当前遍历的节点*/public void traversal(TreeNode root) {if (root == null) {return; // 递归终止条件：空节点直接返回}traversal(root.left);  // 先遍历左子树list.add(root.val);    // 再访问根节点，将值加入列表traversal(root.right); // 最后遍历右子树}
}