倍增：快速幂

题目：P1226 【模板】快速幂 - 洛谷

题目概述：求  ？^ ?  % ？等于多少

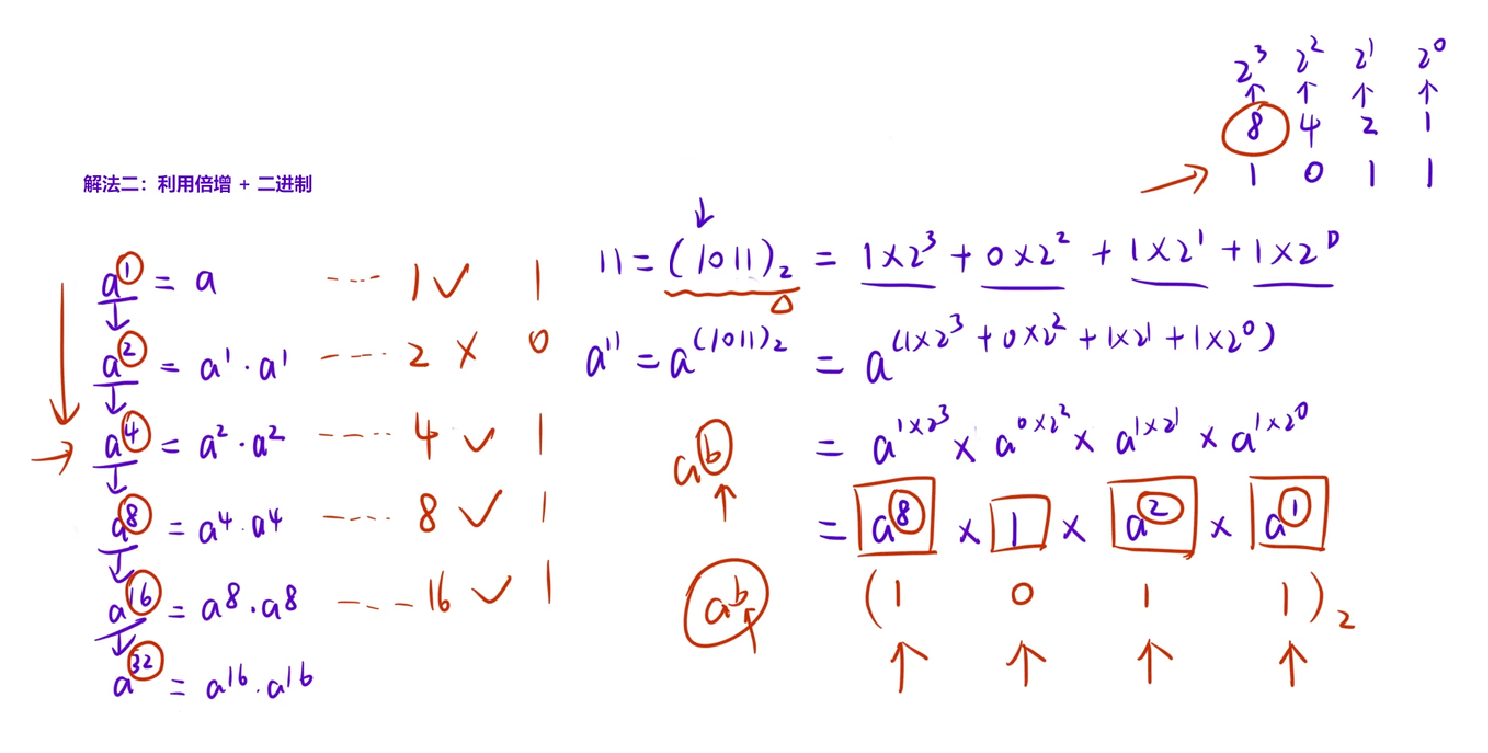
关键代码分析：

LL qpow(LL a, LL b, LL p)//？的 ？次方 %几 
{
    LL ret = 1;   
    while(b) 
    {
        // b&1 检查当前b的最低位是否为0，就是判断二进制下该位是否有效 
        if (b & 1) ret = ret*a%p;    //如果最低位不是0，就把当前的a乘到结果中然后取模 
        a = a*a%p;     // 将a平方，并对p取模，这对应指数每右移一位，底数就要平方一次 
        b >>= 1;         // 指数 b每次被右移一位（b >>= 1），相当于每次将 b除以2，直到 b变为0。循环次数等于 b的二进制位数，即 ⌊log2​b⌋+1   例如 b=16（二进制10000），循环5次
    }
    return ret;
 } 

总代码：

#include <iostream>using namespace std;typedef long long LL;LL a, b, p;LL qpow(LL a, LL b, LL p)//？的 ？次方 %几 
{LL ret = 1;//ret=1 while(b) {if (b & 1) ret = ret*a%p;a = a*a%p;b >>= 1;}return ret;} int main()
{cin >> a >> b >> p;printf("%lld^%lld mod %lld=%lld",a, b, p, qpow(a, b, p));return 0;
}

时间复杂度：O（log b）

由b >>= 1主导，相当于/2