《传感器与检测技术》第 2 章 电阻式传感器原理与应用
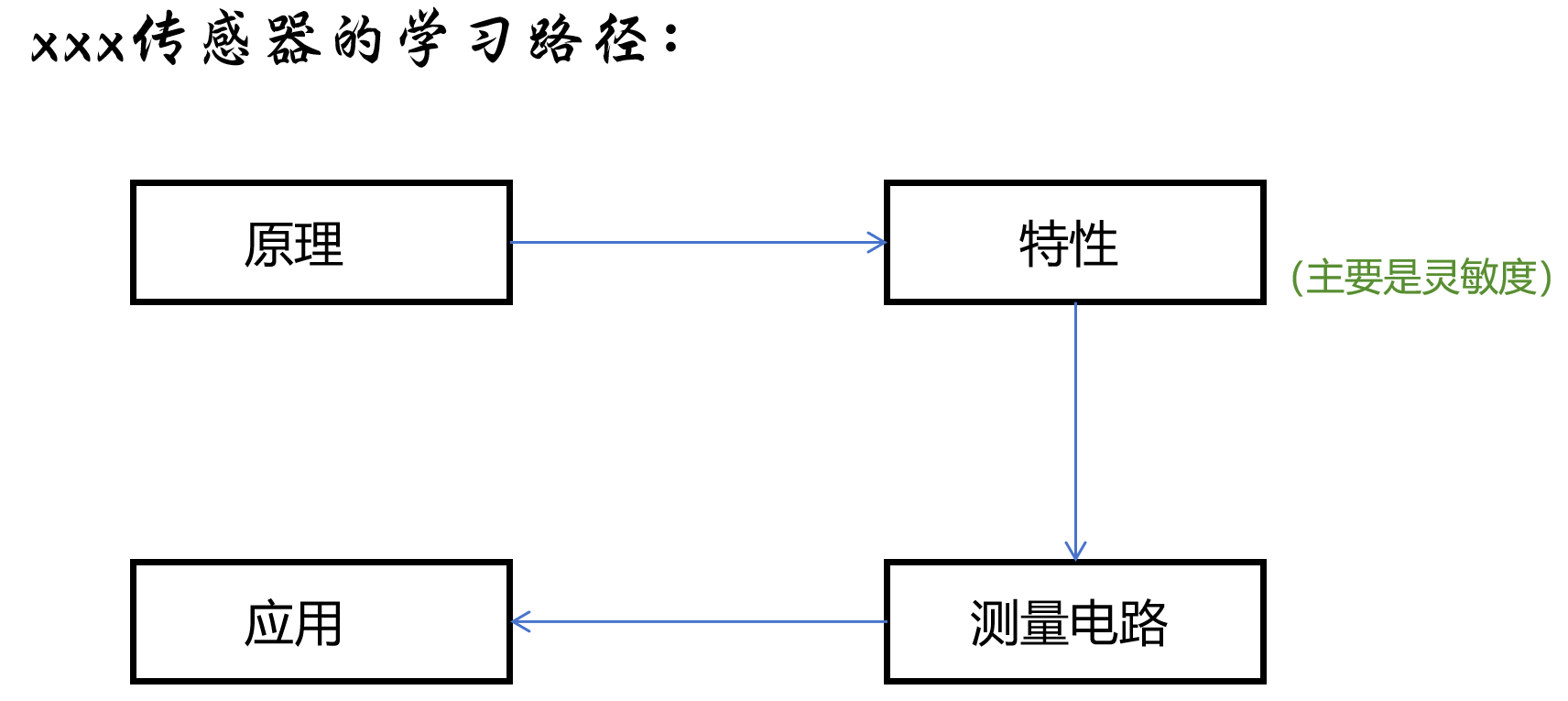
【引言】
电阻式传感器的基本原理是:将被测非电量的变化转变成电阻值的变化,通过测量电阻值达到测量非电量的目的。
按其工作原理,可分为:
- 变阻器式(电位器式) ——滑动变阻器
- 电阻应变式
- 压阻式
- 热电阻式
传感器。
电阻式传感器的应用:可以测量形变、压力、力、位移、加速度和温度等非电量。
本章介绍电阻应变片和压阻式传感器的原理及应用,热电阻式传感器在第6章介绍。




2.1 电阻应变式传感器
电阻应变式传感器具有悠久的历史。由于它具有结构简单、体积小、使用方便、性能稳定、可靠、灵敏度高、动态响应快、适合静态及动态测量、测量精度高等诸多优点,因此是目前应用最广泛的传感器之一。
电阻应变式传感器由弹性元件和电阻应变片构成。
- 当弹性元件感受被测物理量时,其表面产生应变,粘贴在弹性元件表面的电阻应变片的电阻值将随着弹性元件的应变而相应变化。
- 通过测量电阻应变片的电阻值变化,可以用来测量位移、加速度、力、力矩、压力等各种非电量。
2.1.1 电阻应变片的工作原理
(1)金属的电阻应变效应
电阻应变片的工作原理是基于金属的电阻应变效应。
金属的电阻应变效应:金属丝的电阻,随着它所受的机械形变(拉伸或压缩)的大小,而发生相应变化的现象,称为金属的电阻应变效应。
现有如图2.1.1所示的一根金属丝,其电阻设为R,电阻率为ρ,截面积为S,长度为l。
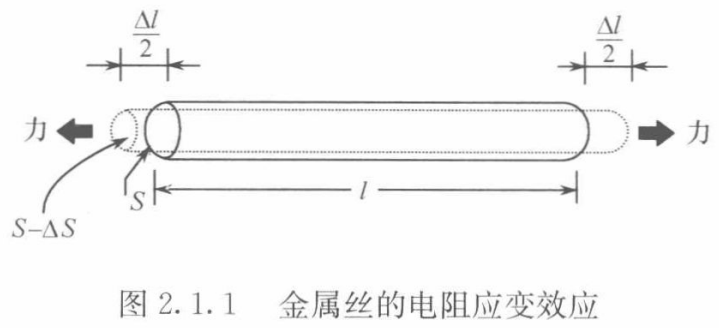
则电阻的表达式为

当金属丝受到拉力作用时,金属丝将沿轴线伸长,伸长量设为∆l,截面积相应减小∆S,电阻率的变化设为∆ρ。
则电阻的相对变化量为

推导:对R求全微分dR,再带入可得
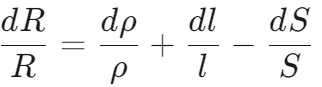


对于半径为r的圆导体:![]() 。(推导:对S求微分dS)
。(推导:对S求微分dS)
又由材料力学可知,在弹性范围内:![]() 。
。
代入式(2.1.2)可得电阻相对变化量
式中单项含义:
- ε为圆导体的纵向应变——其数值一般很小,常以微应变度量;1με =
mm/mm
- μ为金属丝材料的泊松比——一般金属μ为0.3~0.5;
- λ为压阻系数——与材质有关;
- σ为应力值——σ = Eε
- E为材料的弹性模量;
式中组合项含义:
- (1+2μ)ε表示由于几何尺寸变化而引起电阻的相对变化量;
- λEε表示由于材料电阻率的变化而引起电阻的相对变化量;
不同属性的导体,这两项所占的比例相差很大。
通常把单位应变所引起的电阻相对变化称为金属丝的灵敏系数,并用
表示,则
(理论计算)

K0与金属材料及其形状有关。
显然K0越大,单位纵向应变所引起的电阻相对变化越大,说明越灵敏。
大量实验证明,在金属丝拉伸极限内,电阻的相对变化与应变成正比,即K0为常数。
因此,式(2.1.3)可表示为

(2)电阻应变片的结构与种类
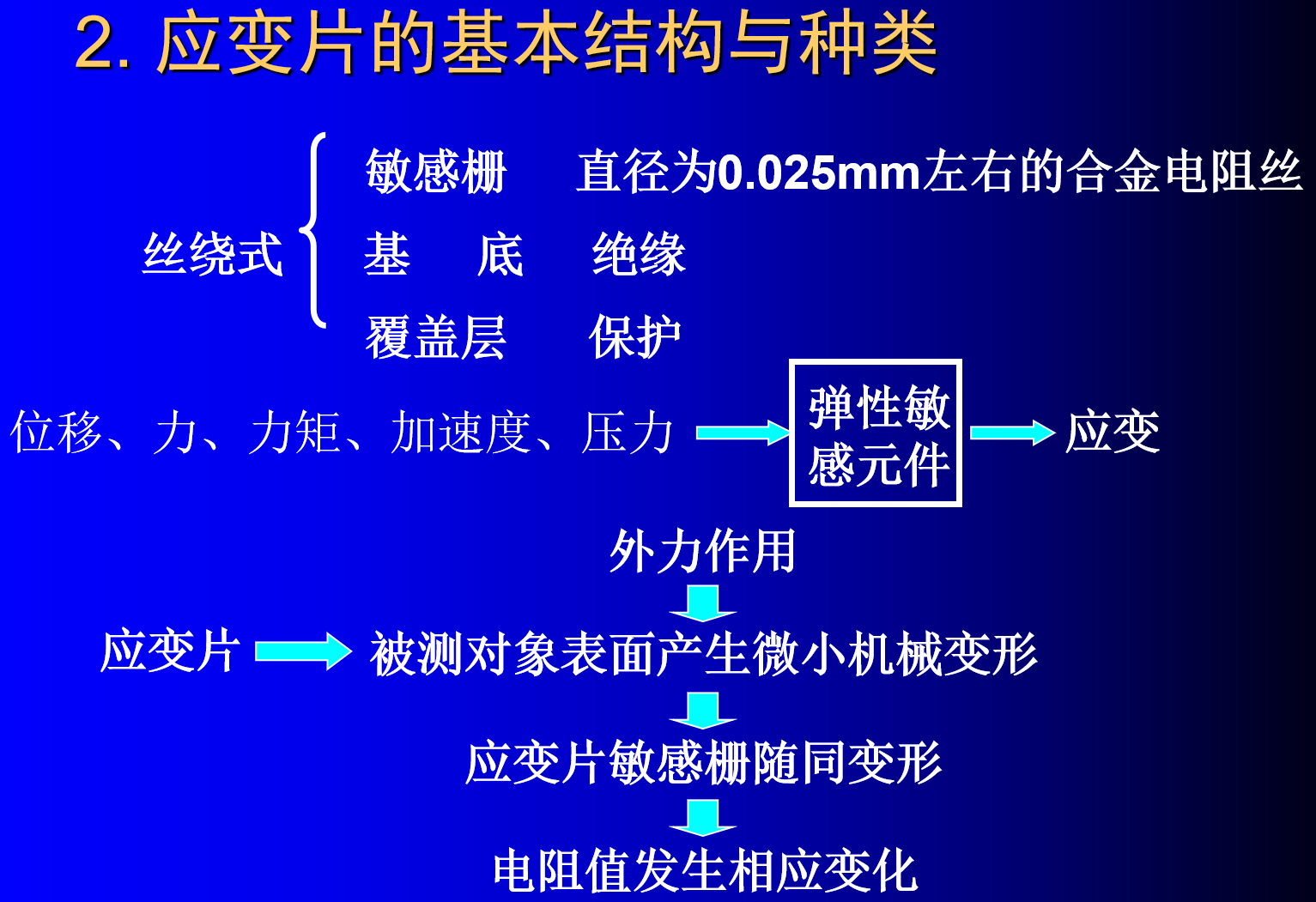
电阻应变片分为丝式应变片、箔式应变片、薄膜应变片3种。
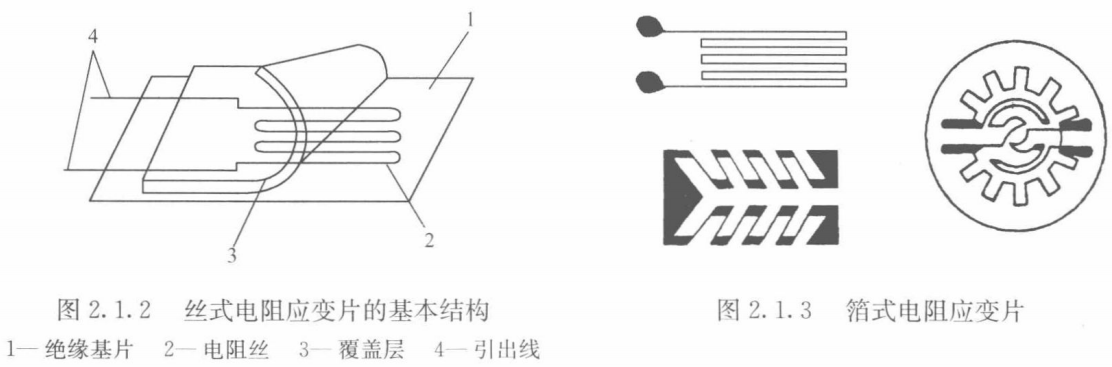
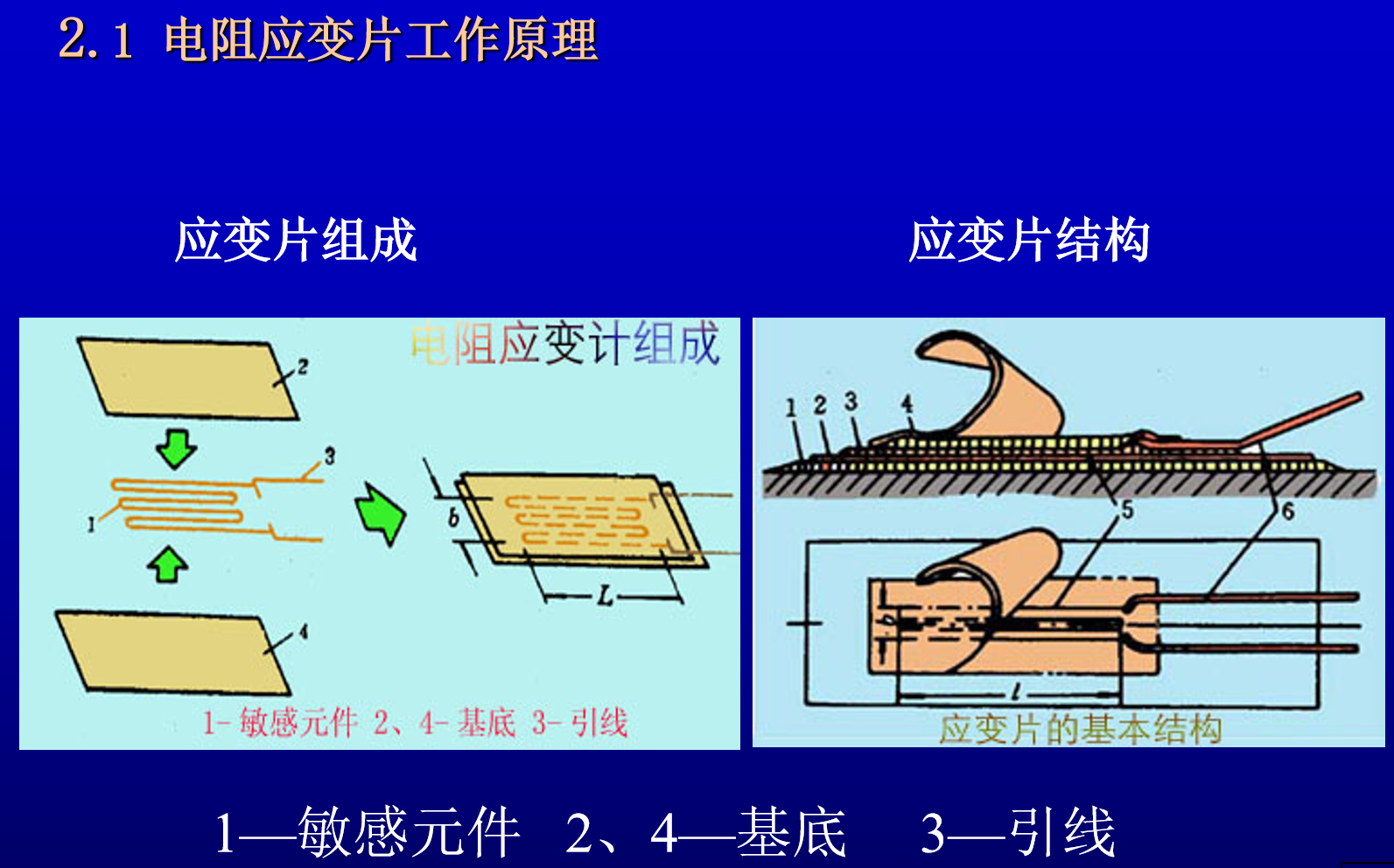
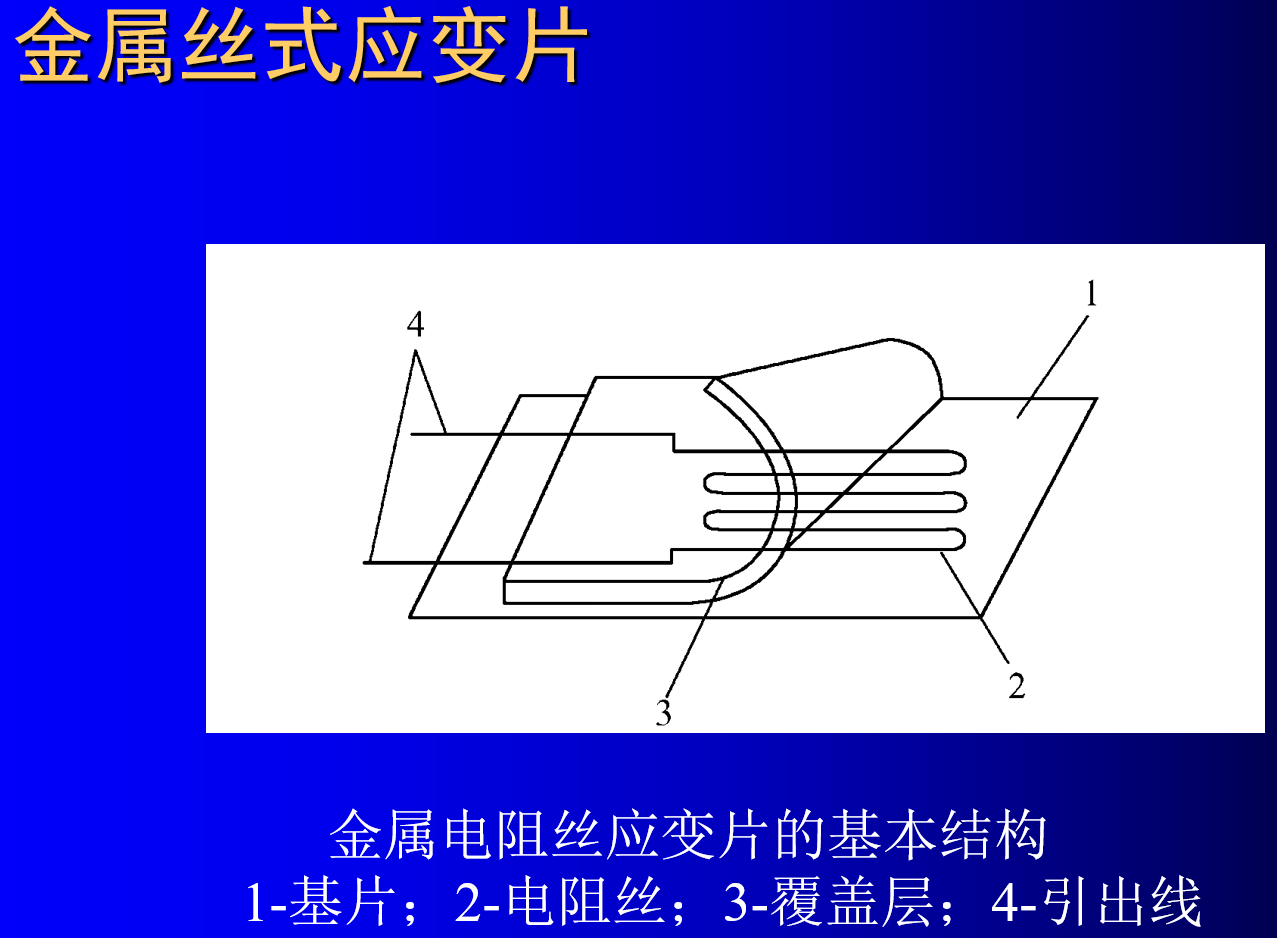
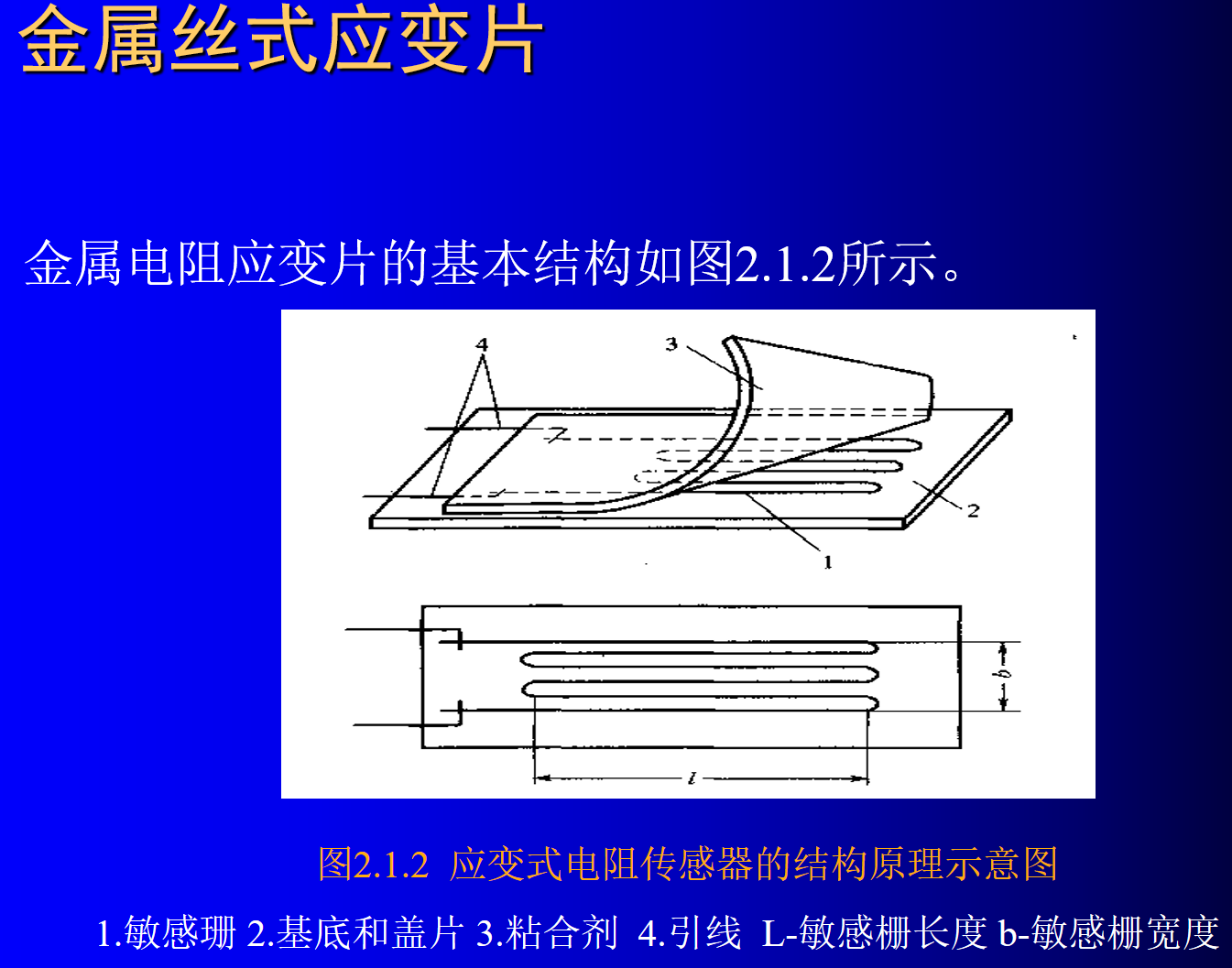
电阻应变片的基本结构大体相同,使用最早的是丝式电阻应变片,如图2.1.2所示。
- 将直径约为0.025mm的高电阻率的电阻丝,弯曲成栅状电阻体2,粘贴在绝缘基片1和覆盖层3之间,由引线4与外部电路相连。
- 这样构成的应变片再通过黏结剂与感受被测物理量的弹性体黏结。


对于电阻应变片,金属材料的电阻率随应变产生的变化很小,可忽略,由式(2.1.3)可得
![]()
由此可见,
- 应变片电阻的相对变化与应变片纵向应变成正比。
- 并且对同一金属材料,K0=1+2μ是常数。
一般用于制造丝式电阻应变片的金属丝,其灵敏系数多为1.7~3.6。(裸丝灵敏系数)




2.1.2 电阻应变片的特性
在实际应用中,选用电阻应变片时,要考虑应变片的性能参数。
应变片的性能参数主要有:
- 应变片的电阻、灵敏度、允许电流和应变极限等。
- 用于动态测量时,还应当考虑应变片本身的动态响应特性。
市售的金属电阻应变片的电阻已趋于标准化,主要规格有60Ω、120Ω、350Ω、600Ω和1000Ω等。
其中120Ω的用得最多。

(1)电阻应变片的灵敏系数
- 将金属单丝做成电阻应变片后,其电阻的应变特性与金属单丝时是不同的。
- 因此必须通过实验重新测定。(K0:理论;K:实测)
此实验必须按规定的统一标准进行。
实验证明,∆R/R与ε的关系在很大范围内仍然有很好的线性关系,即
式中,K称为电阻应变片的灵敏系数。
- 实验表明,电阻应变片的灵敏系数K小于金属单丝的灵敏系数K0。
- 究其原因,主要是在应变片中存在着所谓的横向效应。
电阻应变片的灵敏系数K是通过抽样测定得到的,产品包装上标明的“标称灵敏系数”是出厂时测定的该批产品的平均灵敏系数。

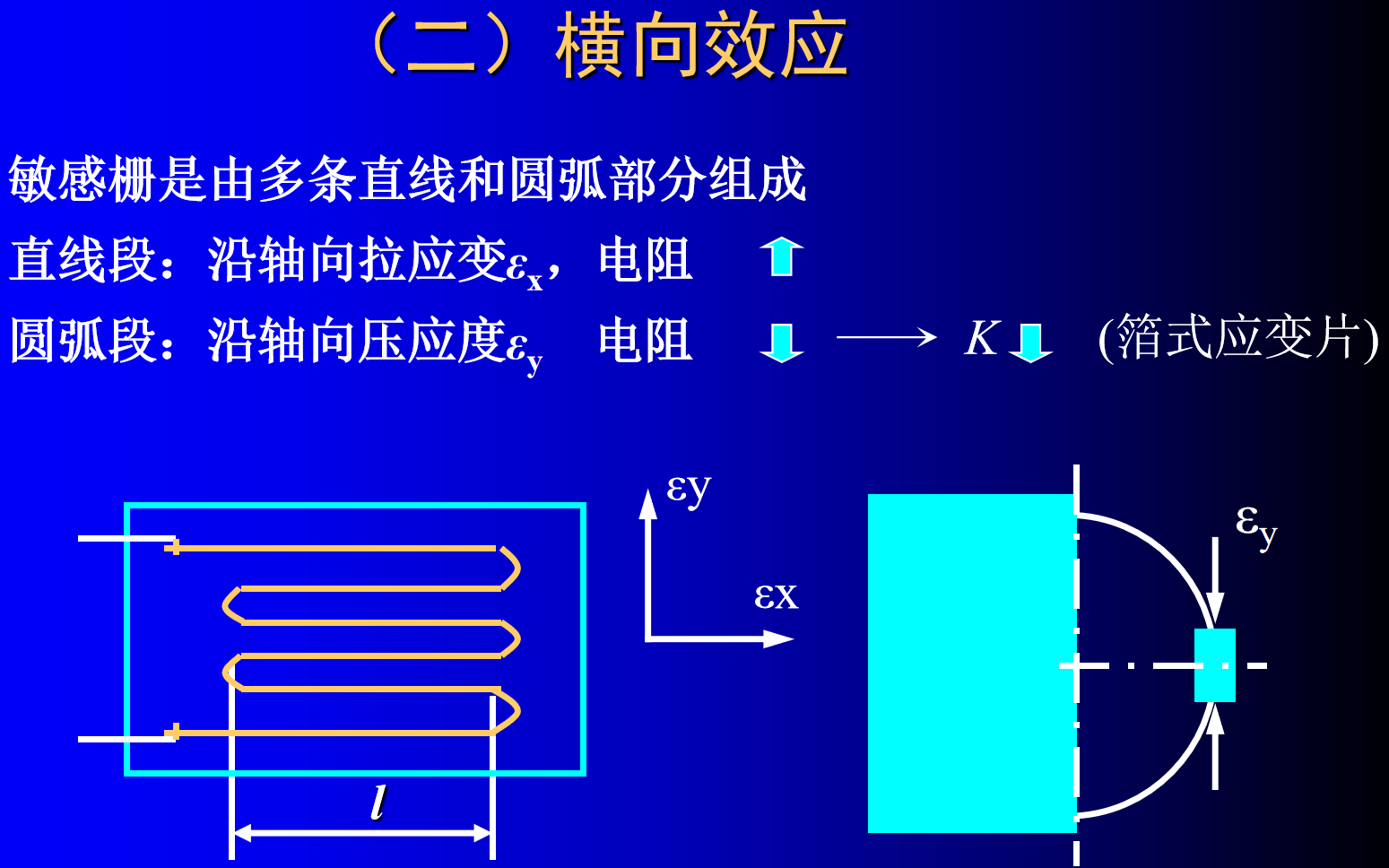
(2)横向效应
应变片的敏感栅除了有纵向丝栅,还有圆弧形或直线形的横栅。
横栅既对应变片轴线方向的应变敏感,又对垂直于轴线方向的横向应变敏感。
当电阻应变片粘贴在一维拉力状态下的试件上时,应变片的纵向丝栅因发生纵向拉应变,使其电阻值增加。
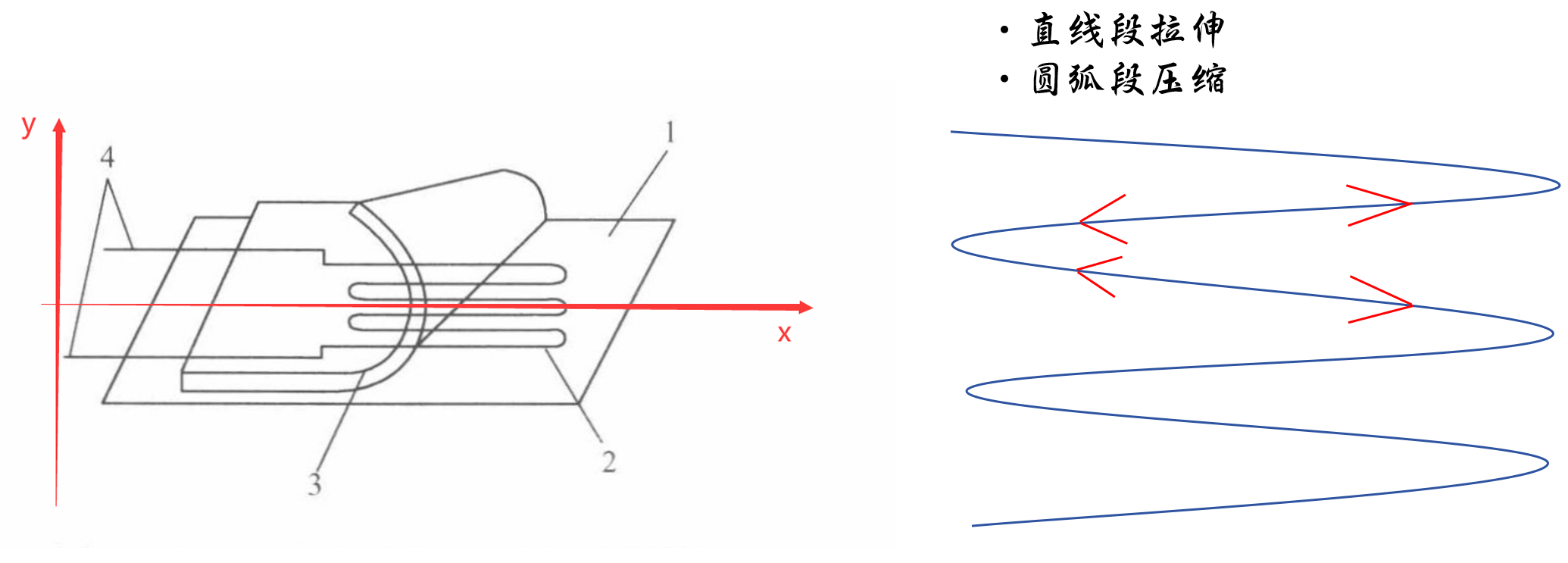
而应变片的横栅因同时感受纵向拉应变,和横向压应变
,使其电阻值减小。
因此,应变片的横栅部分将纵向丝栅部分的电阻变化抵消了一部分,从而降低了整个应变片的灵敏度。这就是应变片的横向效应。
横向效应给测量带来了误差,其大小与敏感栅的构造及尺寸有关。
敏感栅的纵向丝栅越窄、越长,而横栅越宽、越短,则横向效应的影响越小。


(3)温度误差及其补偿
① 温度误差


② 温度补偿方法
应变片的温度补偿方法通常有:电桥补偿、应变片自补偿两大类。
(Ⅰ)电桥补偿法(补偿片法)

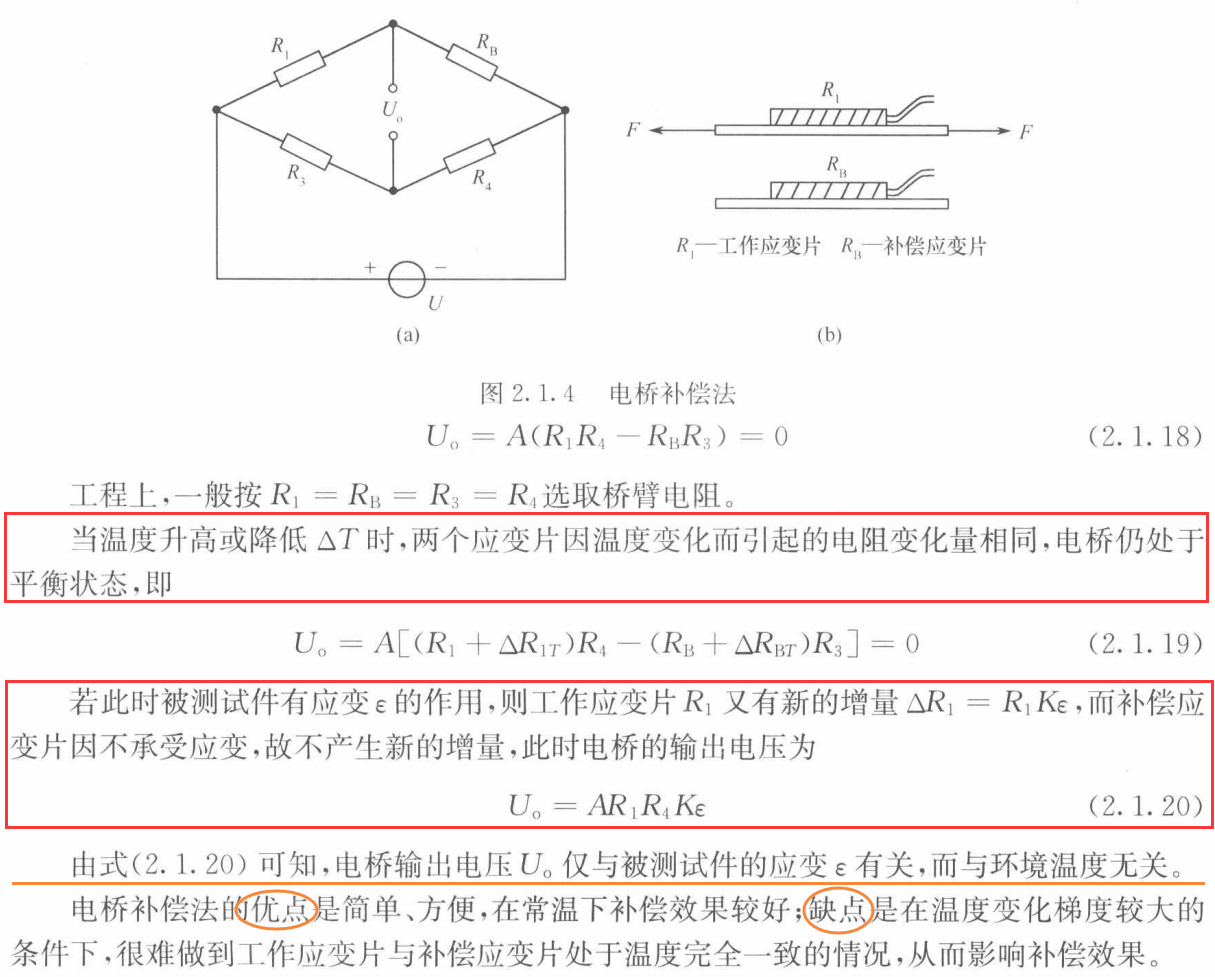
(Ⅱ)应变片自补偿法

![]()
(Ⅲ)热敏电阻补偿法
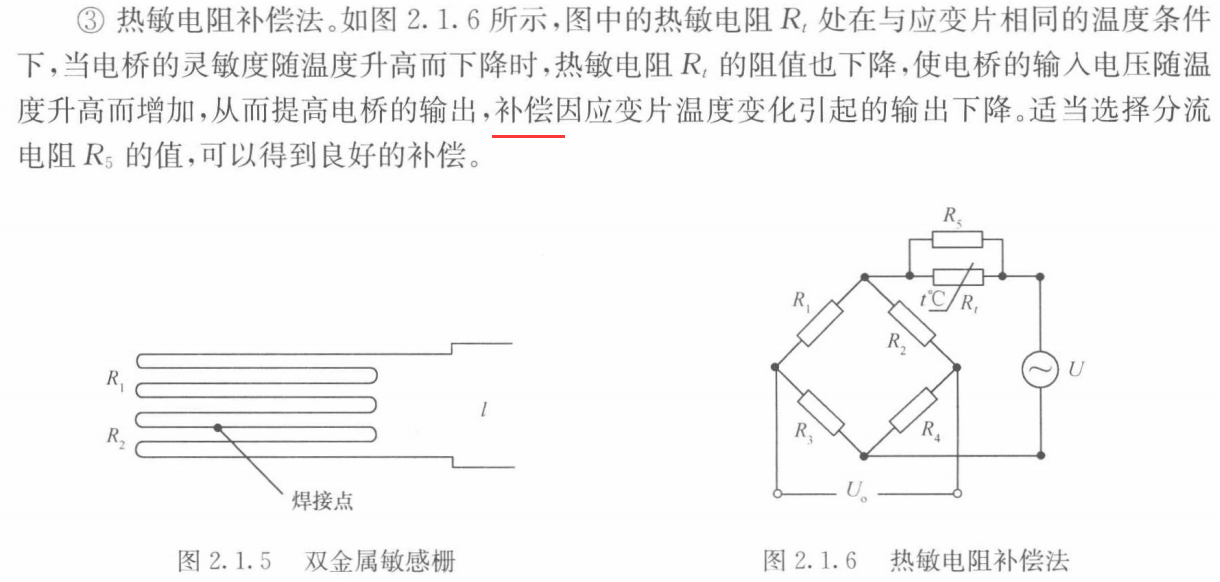
2.1.3 电阻应变片的测量电路
应变片可以将应变转换为电阻的变化,为了显示与记录应变的大小,还要把电阻的变化再转换为电压或电流的变化,因此,需要有专用的测量电路。
通常采用直流电桥和交流电桥。
L、C在交流下正常工作,阻抗 jωL(2πfL)、1/jωC(1/2πfC)的表现需要 ω。
下面对直流不平衡电桥进行介绍。
(1)电桥电路的工作原理
由于应变片电桥电路的输出信号一般比较微弱。
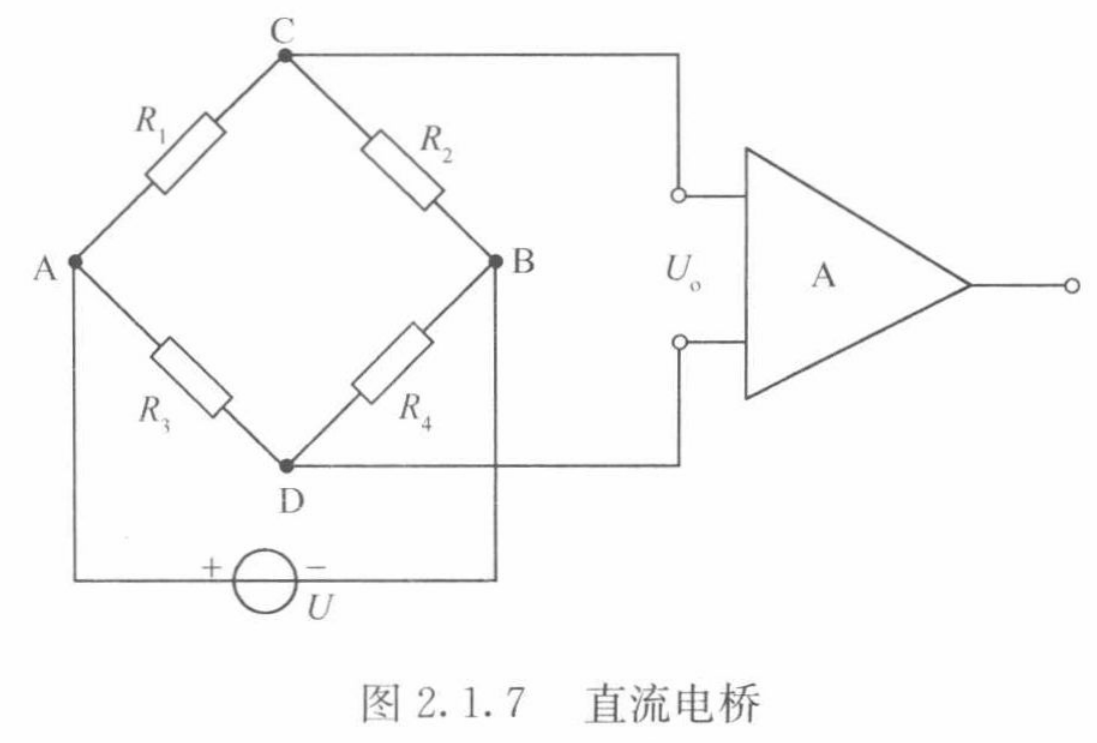
因此目前大部分电阻应变式传感器的电桥输出端与直流放大器相连,如图2.1.7所示。
设电桥各臂的电阻分别为R1、R2、R3和R4,它们可以全部或部分是应变片。
(双臂、全桥:无非线性误差;三臂 == 单臂:引入非线性误差)
由于直流放大器的输入电阻比电桥电阻大得多,因此可将电桥输出端看成开路。
这种电桥称为“电压输出桥”,输出电压Uo为
把电源放成
就为正了,但是取绝对值就不影响。
当R1R4=R2R3时,电桥处于平衡状态,输出电压Uo= 0。(对臂积等、邻臂比等)
若电桥各臂均有相应的电阻增量∆R1、∆R2、∆R3和∆R4,则由式(2.1.23)得
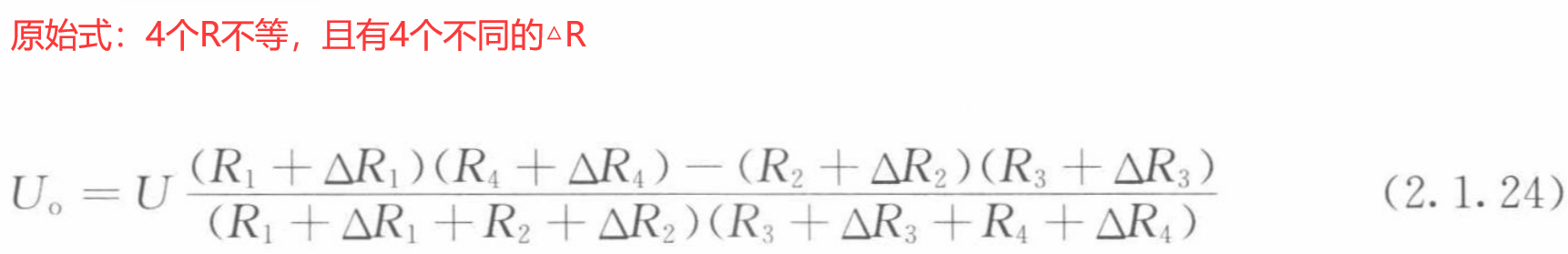

注:同种材料,K相同。
(2)非线性误差及其补偿
式(2.1.27)的线性关系是在应变片的参数变化很小,即∆R << R的情况下得出的。
若应变片所承受的应变太大,则上述假设不成立,电桥输出与应变之间不再呈现严格线性,而是具有非线性误差,呈现非线性关系。
在这种情况下,用按线性关系刻度的仪表进行测量必然带来非线性误差。
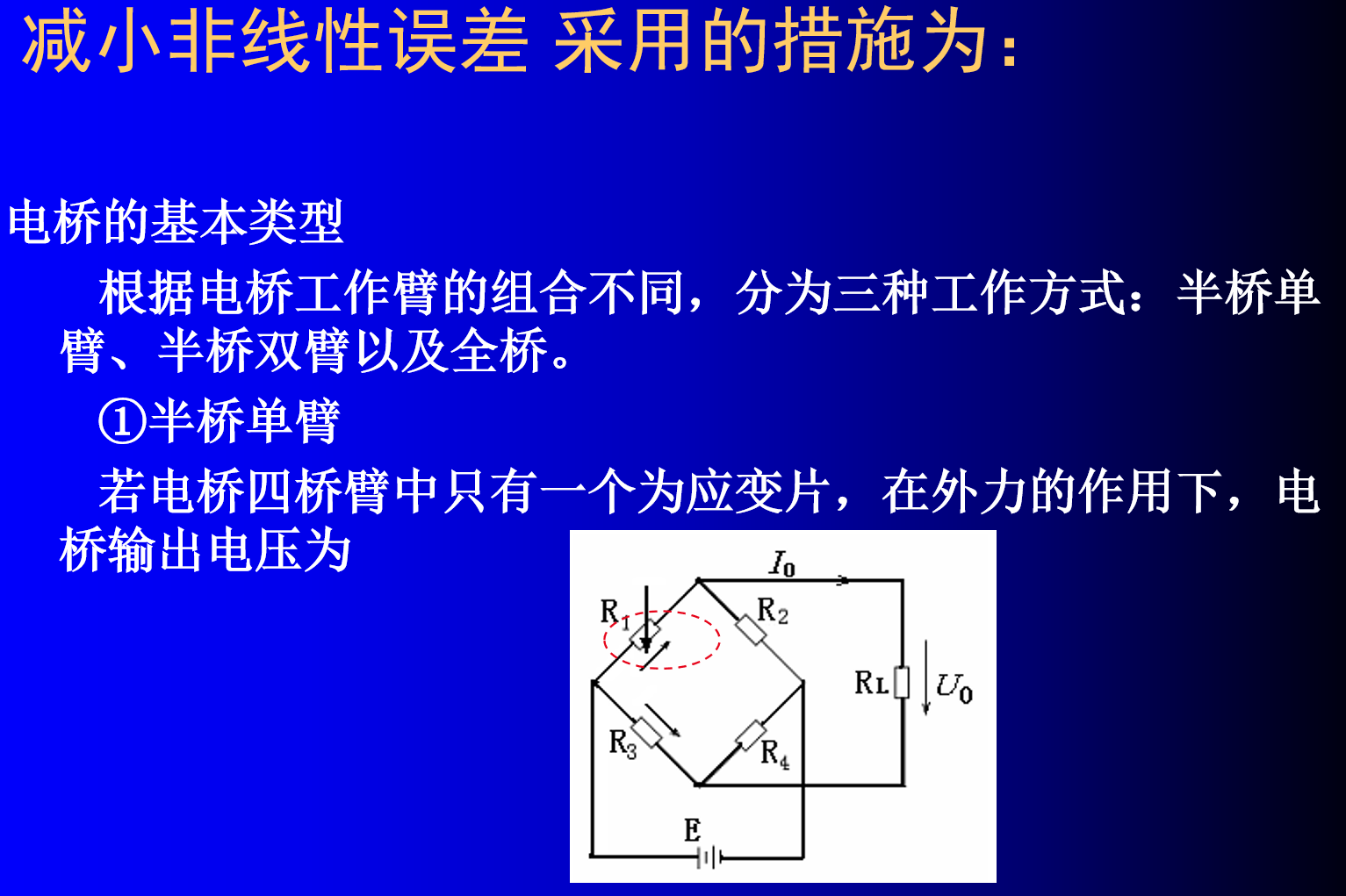
① 半桥单臂
当考虑电桥单臂工作时,即R1桥臂变化∆R。
(Ⅰ)理想线性公式(∆R << R)
由式(2.1.26)得理想的线性关系为
![]()
(Ⅱ)灵敏度(Sensitivity)
结论:电桥单臂工作时,灵敏度是源电压的1/4。
(Ⅲ)实际工作公式(不考虑∆R << R)
而由式(2.1.25)得电桥的实际输出电压为

(Ⅳ)非线性误差
则电桥的相对非线性误差为
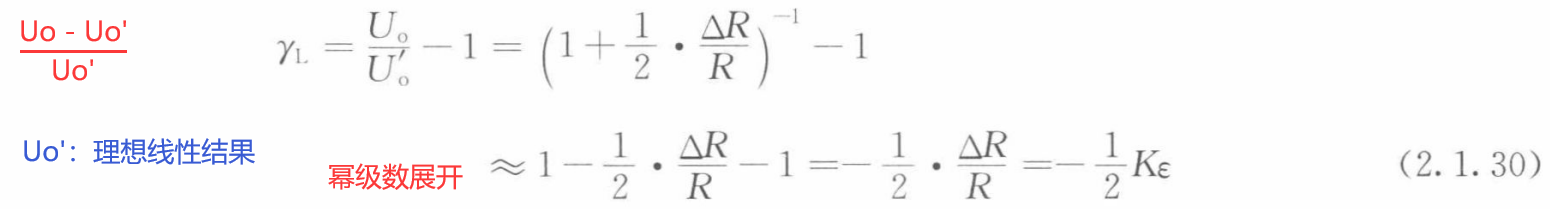
由上式可知,Kε越大,也越大。
当x→0时,有泰勒展开式:
![]()
![]()
在|x| < 1时收敛。
理解1:微小量展开
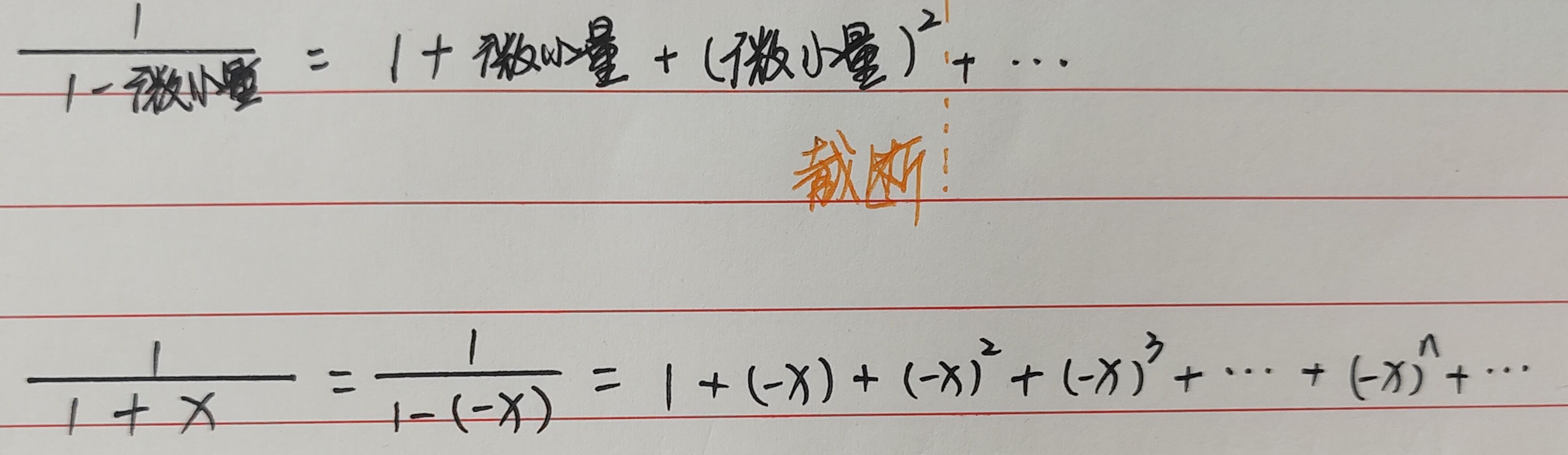
理解2:减法是本体
为了消除非线性误差,在实际应用中,常采用半桥差动电路、全桥差动电路。
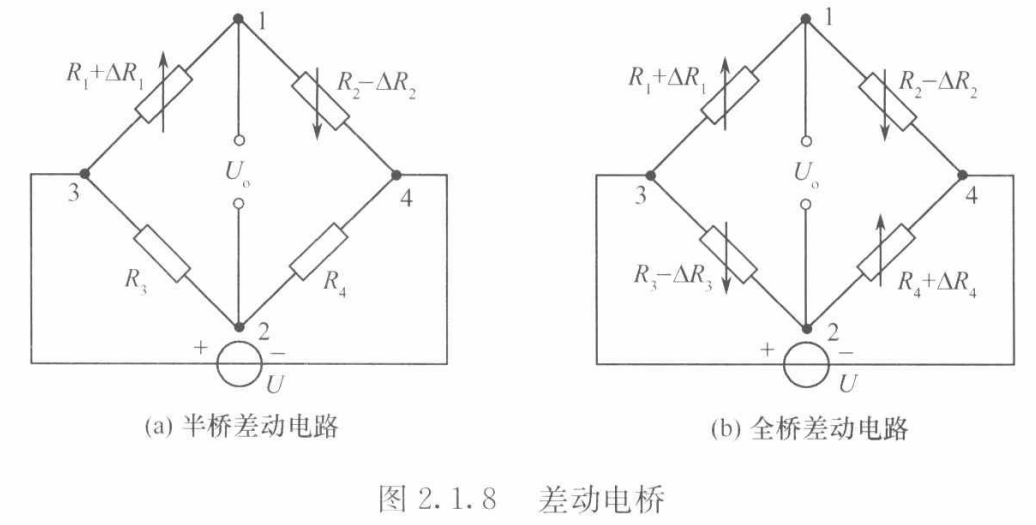
如图2.1.8所示,以改善非线性误差和提高输出灵敏度。
差动:R1与R2极性相反,当R1在被拉伸时,R2在被压缩。









② 半桥双臂
图2.1.8(a)为半桥差动电路,在传感器中经常使用这种接法。粘贴应变片时,使两个应变片一个受拉、一个受压,应变·符号相反,工作时将两个应变片接入电桥的相邻两臂。
设电桥在初始时是平衡的,且为等臂电桥,考虑到![]()
则由式(2.1.25)得:
半桥差动电路的输出电压为
由上式可见:
- 半桥差动电路不仅能消除非线性误差;(严格线性)
- 而且还使电桥的输出灵敏度比单臂工作时提高了一倍;S = U/2。
- 同时还能起温度补偿作用。
注:三臂 == 单臂,又会引入非线性误差。
③ 全桥
如果按图2.1.8(b)所示构成全桥差动电路,同样考虑到![]()
![]() 。
。
则由式(2.1.25)得:
全桥差动电路的输出电压为
可见:
- 全桥差动电路的输出灵敏度是电桥单臂工作时的4倍;
- 非线性误差也得以消除;
- 同时还具有温度补偿的作用。
该电路得到了广泛的应用。

2.1.4 电阻应变式传感器的应用
电阻应变片除测量试件应力、应变外,还被制造成多种应变式传感器来测量力、扭矩、位移、压力、加速度等物理量。
- 电阻应变式传感器由弹性元件和粘贴于其上的应变片构成。
- 弹性元件将获得与被测量成正比的应变,再通过应变片转换为电阻的变化后输出。
下面介绍其典型应用。
(1)应变式力传感器
被测量为载荷或力的应变式传感器,统称为应变式力传感器。它是工业测量中用得较多的一种传感器,量程从几克到几百吨,主要用作各种电子秤与材料试验机的测力元件、发动机的推力测试、水坝坝体承载状况监测等。
应变式力传感器要求有较高的灵敏度和稳定性,当传感器受到侧向作用力或力的作用点发生轻微变化时,不应对输出有明显的影响。
应变式力传感器的弹性元件有柱(筒)式、悬臂式、环式、框式等。
① 柱(筒)式力传感器
圆柱(筒)式力传感器的弹性元件分为实心和空心两种,如图2.1.9(a)、(b)所示。
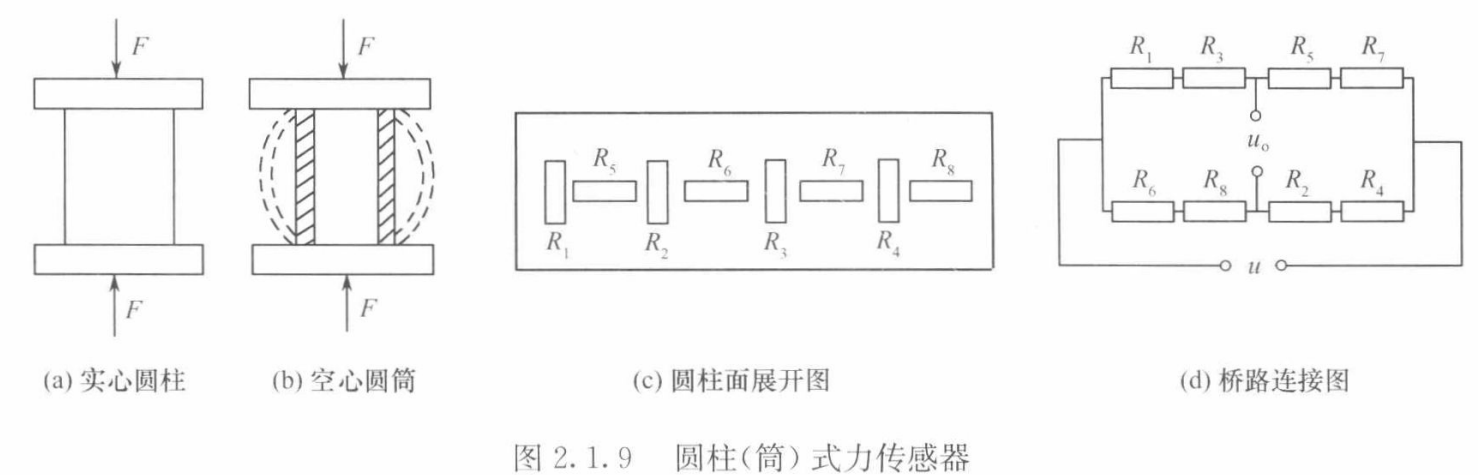
实心圆柱可以承受较大的载荷,在弹性范围内,应力与应变成正比关系,即
![]()
式中:
- ε为应变;(轴向应变、纵向应变)
- F为作用在弹性元件上的集中力;
- S为圆柱的横截面积;
- E为弹性元件的弹性模量;
- σ = F/S为应力;(单位面积压力)

空心圆筒多用于小集中力的测量。
应变片粘贴在弹性体外臂应力分布均匀的中间部分,对称地粘贴多片,电桥接线时应尽量减小载荷偏心和弯矩的影响,应变片粘贴在圆柱面上的位置及其在桥路中的连接如图2.1.9(c)、(d)所示。
- R1和R3串接,R2和R4串接,并置于桥路对臂上,以减小弯矩影响。
- 横向贴片做温度补偿用。
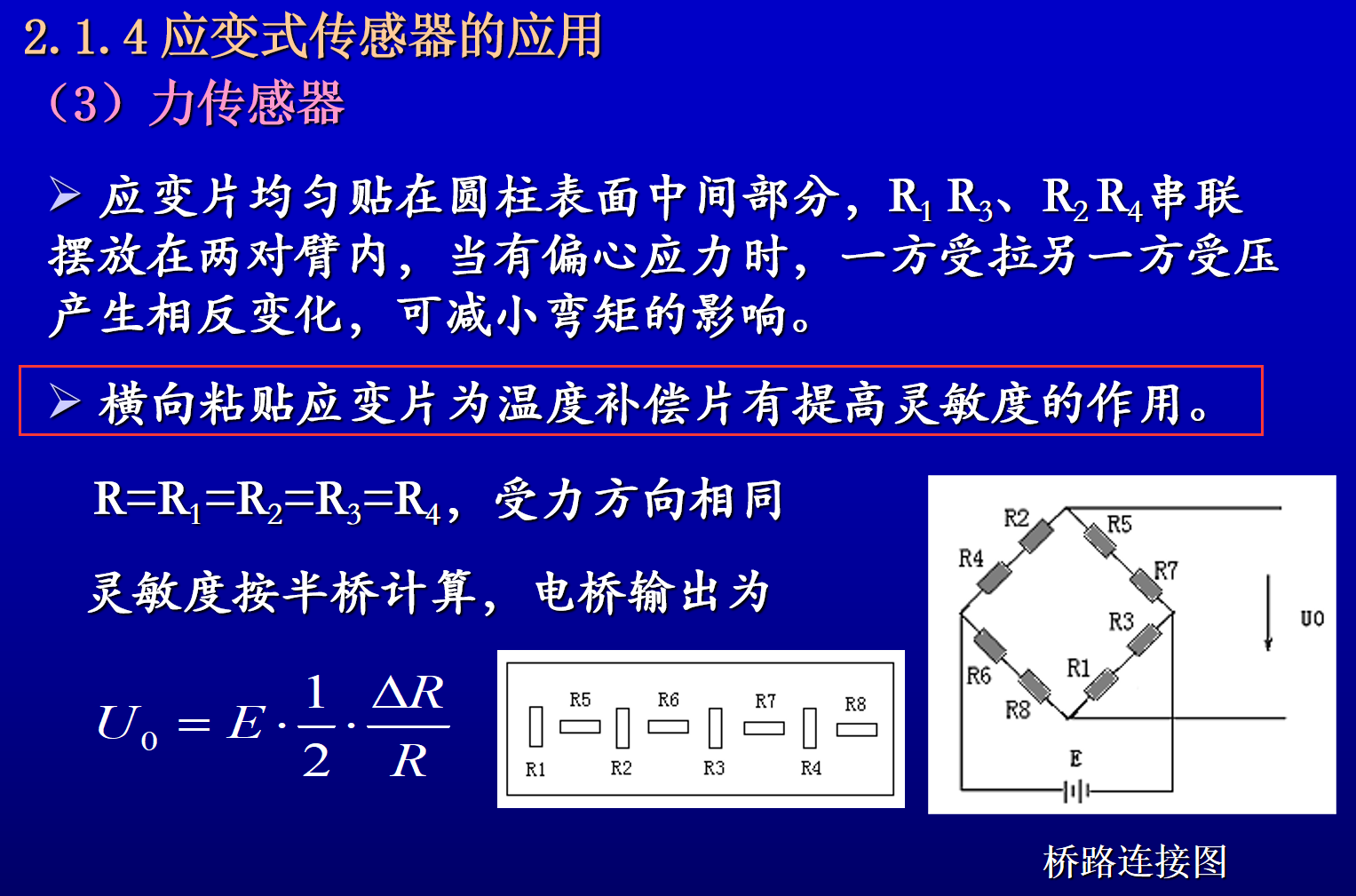
当被测物体比较大(大桥、……),一个电阻应变片只能感受很小范围内的应变,就会让分布在多个位置的R的变化均值作为∆R1,以此类推……
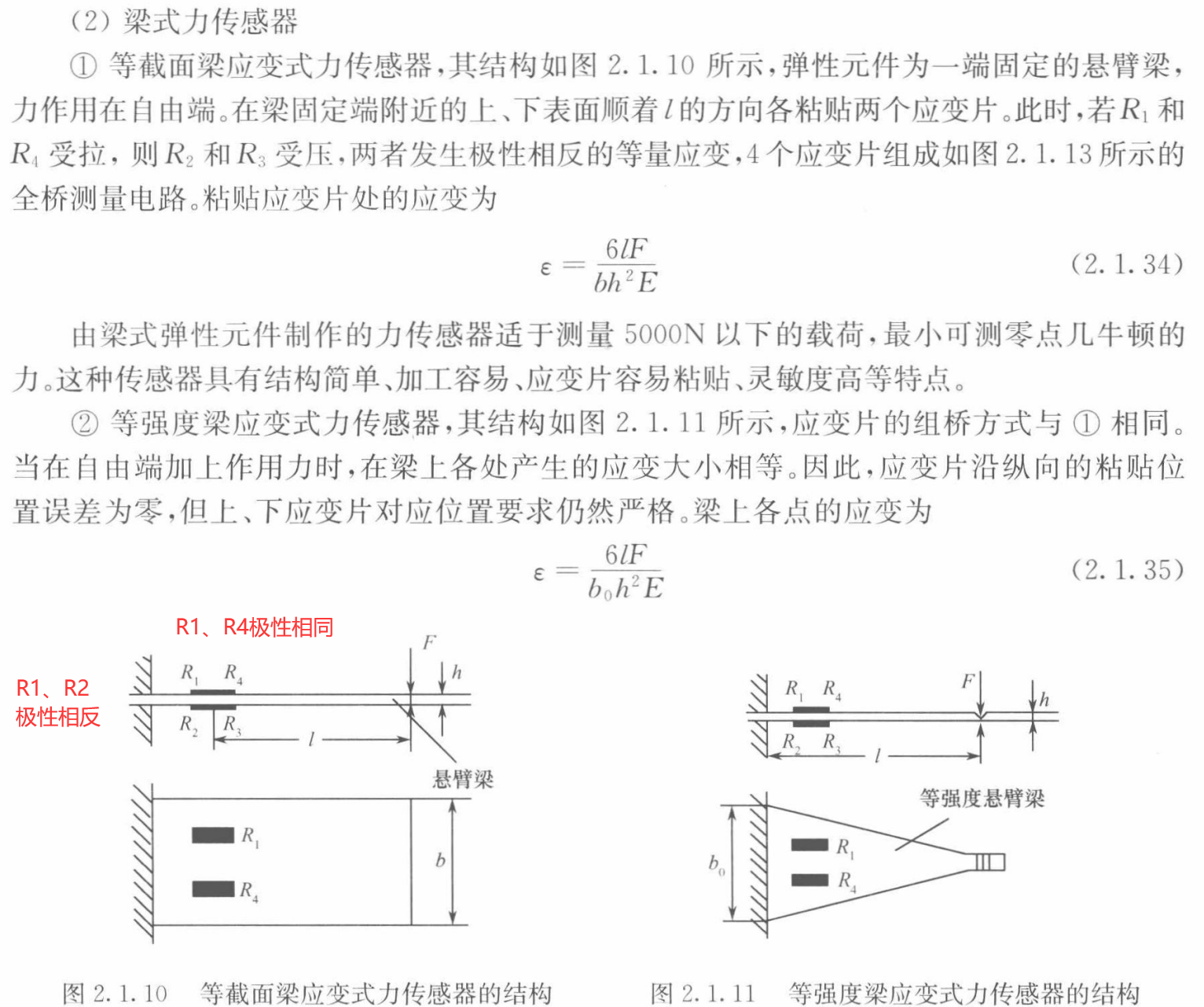
……
(4)应变式加速度传感器
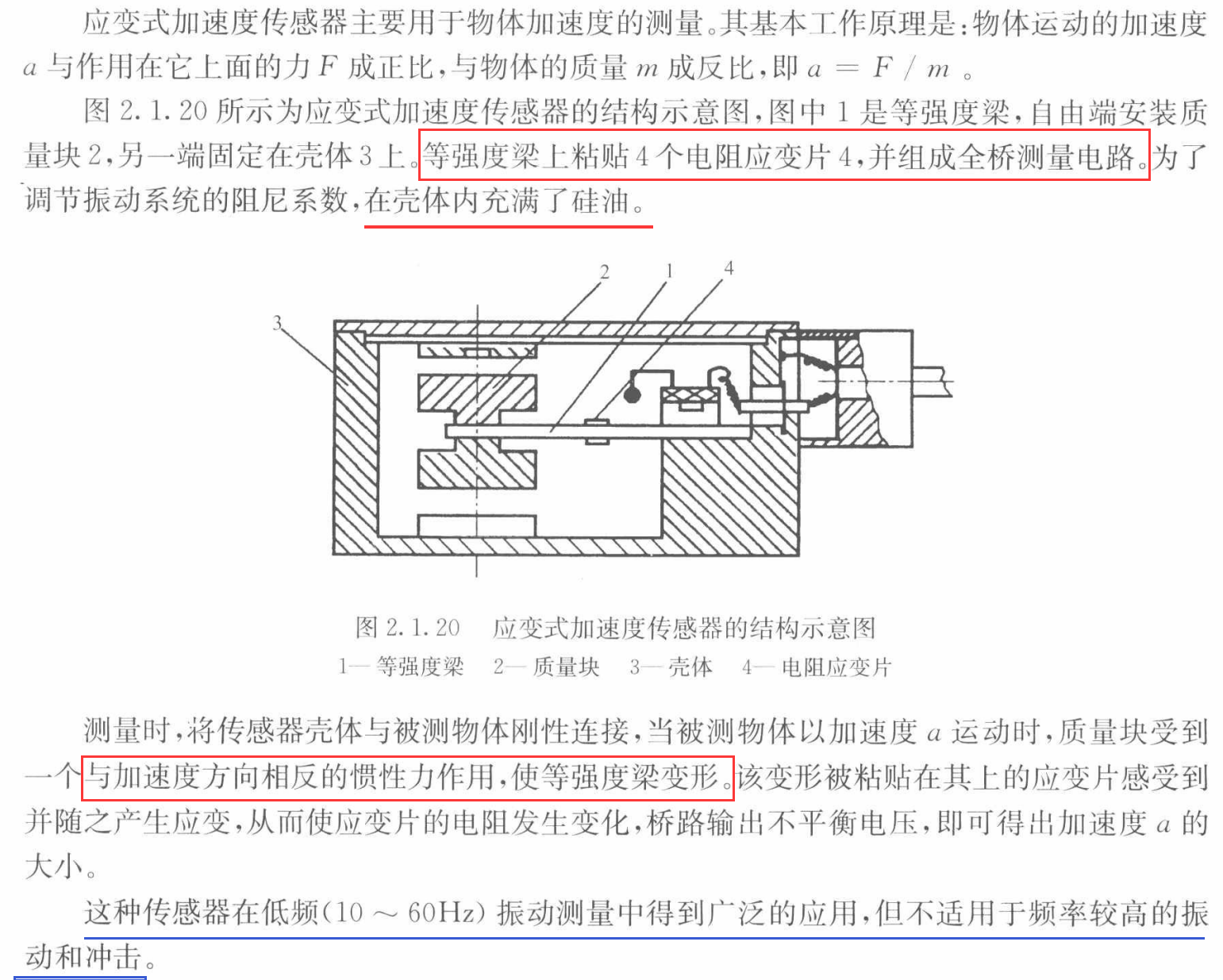


……
2.2 压阻式传感器
电阻应变片性能稳定、精度较高,至今还在不断地改进和发展,并在一些高精度应变式传感器中得到了广泛的应用。
但其主要缺点是灵敏系数较小。
而20世纪50年代中期出现的半导体应变片可以改善这一不足,其灵敏系数比电阻应变片约高50倍。
主要有:体型半导体应变片、扩散型半导体应变片。
- 用半导体应变片制作的传感器称为压阻式传感器;
- 其工作原理基于半导体的压阻效应。
2.2.1 半导体的压阻效应
半导体的压阻效应:是指单晶半导体在沿某一轴向受外力作用时,其电阻率发生很大变化的现象。
不同类型的半导体,施加载荷的方向不同,压阻效应也不一样。
目前使用最多的是单晶硅半导体。

2.2.2 半导体应变片
(1)结构形式及特点
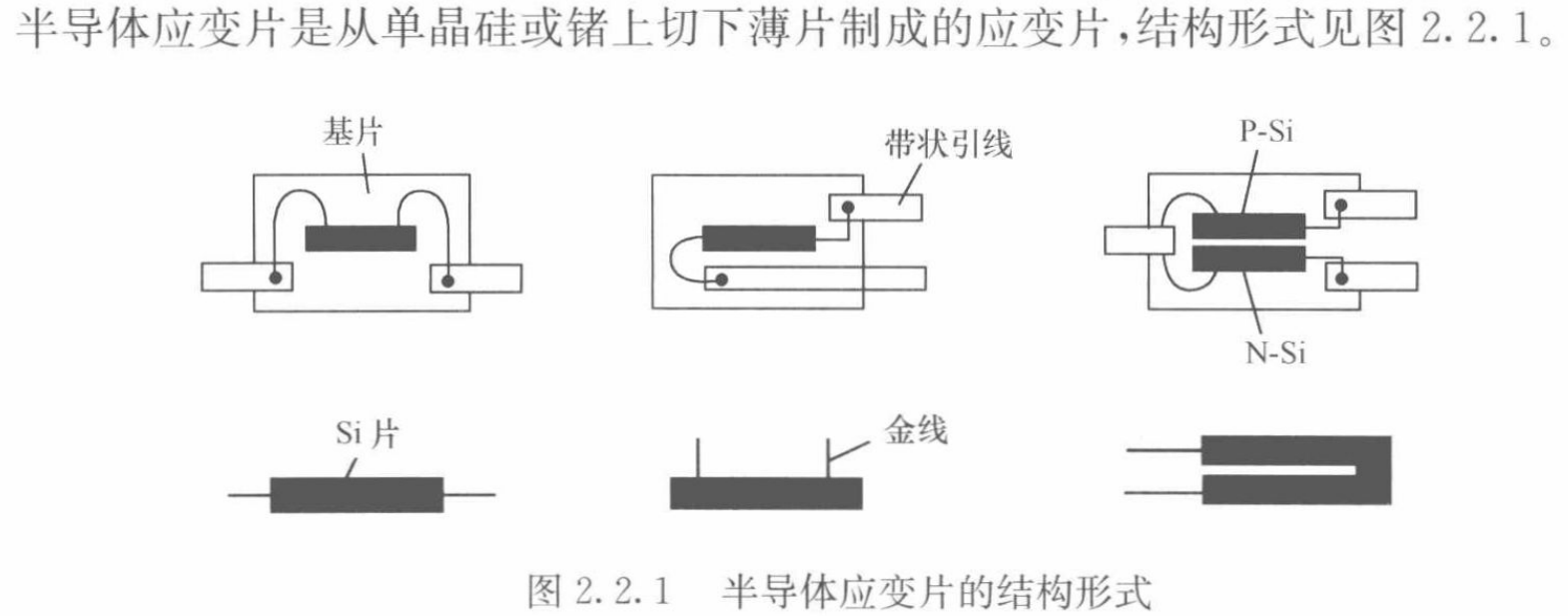
- 半导体应变片的主要优点是灵敏系数比电阻应变片的灵敏系数大数十,通常不需要放大器就可以直接输入显示器或记录仪,可简化测试系统。
- 另外,它的横向效应和机械滞后极小。
- 但是,半导体应变片的温度稳定性和线性度比电阻应变片差得多,很难用它制作高精度的传感器,只能作为其他类型传感器的辅助元件。
- 近年来,由于半导体材料和制作技术的提高,半导体应变片的温度稳定性和线性度都得到了改善。
(2)测量电路

2.2.3 扩散型压阻式压力传感器
……
2.2.4 压阻式加速度传感器
……
2.2.5 测量电桥及温度补偿
……



