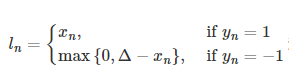【深入浅出PyTorch】--3.2.PyTorch组成模块2

在深度学习模型的训练中，权重的初始值极为重要。一个好的初始值，会使模型收敛速度提高，使模型准确率更精确。一般情况下，我们不使用全0初始值训练网络。为了利于训练和减少收敛时间，我们需要对模型进行合理的初始化。PyTorch也在torch.nn.init中为我们提供了常用的初始化方法。 通过本章学习，你将学习到以下内容：

• 常见的初始化函数

• 初始化函数的使用

目录

1.初始化函数

1.1.初始化函数的封装

2.损失函数

2.1.二分类交叉熵损失

2.2.交叉熵损失函数

2.3.其他损失函数

3.训练与验证

3.1.训练

3.2.验证

4.优化算法

4.1.Optimizer属性

4.2.Optimizer方法

---

1.初始化函数

torch.nn.init 是 PyTorch 中用于神经网络参数（如权重、偏置）初始化的工具模块。它提供了一系列函数，用于对 torch.Tensor （张量）对象进行不同策略的初始化。

核心特点：

• 原地操作 (In-place)：除了 calculate_gain，所有初始化函数的名称都带有下划线后缀（如 uniform_）。这表示它们会直接修改输入的张量（tensor）的值，而不是返回一个新的张量。
• 目的：合理的初始化可以加速模型收敛，避免梯度消失或爆炸等问题。

以下是 torch.nn.init 提供的主要初始化函数：

函数名	描述	关键参数
uniform_(tensor, a=0.0, b=1.0)	从均匀分布 U(a, b) 中采样来初始化张量。	a, b: 分布的上下界。
normal_(tensor, mean=0.0, std=1.0)	从正态分布 N(mean, std) 中采样来初始化张量。	mean, std: 均值和标准差。
constant_(tensor, val)	将张量的所有元素填充为一个常数 val。	val: 要填充的常数值。
ones_(tensor)	将张量的所有元素填充为 1。	无
zeros_(tensor)	将张量的所有元素填充为 0。	无
eye_(tensor)	为 2D 张量创建一个单位矩阵。对于更高维张量，最内层的两个维度构成单位矩阵，其余元素为 0。	无
dirac_(tensor, groups=1)	为卷积层的权重初始化，使得初始时网络为恒等映射（仅适用于 3D, 4D, 5D 的 tensor）。	groups: 卷积分组数。
xavier_uniform_(tensor, gain=1.0)	Xavier/Glorot 均匀初始化。从以 0 为中心，[-limit, limit] 为范围的均匀分布中采样，其中 limit = gain * sqrt(6 / (fan_in + fan_out))。	gain: 缩放因子。
xavier_normal_(tensor, gain=1.0)	Xavier/Glorot 正态初始化。从均值为 0，标准差为 gain * sqrt(2 / (fan_in + fan_out)) 的正态分布中采样。	gain: 缩放因子。
kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')	Kaiming/He 均匀初始化。常用于 ReLU 及其变体激活函数的网络。	a: 负斜率（用于 leaky_relu），mode: 'fan_in' 或 'fan_out'，nonlinearity: 激活函数名。
kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')	Kaiming/He 正态初始化。与 kaiming_uniform_ 类似，但从正态分布采样。	参数同上。
orthogonal_(tensor, gain=1)	生成一个（半）正交矩阵来初始化张量。对于非方阵，会进行奇异值分解（SVD）并用得到的正交基初始化。对 RNN 非常有效。	gain: 应用于正交矩阵的缩放因子。
sparse_(tensor, sparsity, std=0.01)	将张量初始化为一个稀疏矩阵。每个行向量中，有 sparsity 比例的元素被设置为 0，其余元素从 N(0, std) 中采样。	sparsity: 稀疏度（0-1 之间），std: 非零元素分布的标准差。

---

增益计算 (Gain Calculation)

calculate_gain(nonlinearity, param=None)
功能：计算给定非线性激活函数（nonlinearity）的推荐增益（gain）值。这个值通常作为 xavier_* 和 kaiming_* 等初始化方法的 gain 参数传入，以获得更合适的初始化尺度。

常见非线性函数的增益值表

非线性函数 (nonlinearity)	增益 (Gain)
Linear / Identity	1
Conv{1,2,3}D	1
Sigmoid	1
Tanh	5/3 ≈ 1.6667
ReLU	√2 ≈ 1.4142
Leaky ReLU	√(2 / (1 + neg_slope²))

说明：

• Leaky ReLU 的增益取决于其负斜率 neg_slope。例如，当 neg_slope=0.01 时，增益约为 1.4141。
• 使用 calculate_gain 函数可以方便地获取这些值，例如：gain = torch.nn.init.calculate_gain('relu')。

具体每一层设计的参数可以看上一章：

https://blog.csdn.net/qq_58602552/article/details/152280344?spm=1001.2014.3001.5501

举个例子：

import torch
import torch.nn as nn# 定义一个卷积层
conv = nn.Conv2d(1, 3, 3)  # 输入通道1，输出通道3，卷积核大小3x3
# 定义一个全连接（线性）层
linear = nn.Linear(10, 1)  # 输入维度10，输出维度1# 检查 conv 是否是 nn.Conv2d 类型
print(isinstance(conv, nn.Conv2d))    # 输出: True
# 检查 linear 是否是 nn.Conv2d 类型
print(isinstance(linear, nn.Conv2d))  # 输出: Falseprint(conv.weight.data)
print(linear.weight.data)# 对conv进行kaiming初始化
torch.nn.init.kaiming_normal_(conv.weight.data)
print(conv.weight.data)
# 对linear进行常数初始化
torch.nn.init.constant_(linear.weight.data,0.3)
print(linear.weight.data)
# #输出偏置项
# print(conv.bias.data)
# print(linear.bias.data)

1.1.初始化函数的封装

人们常常将各种初始化方法定义为一个initialize_weights()的函数并在模型初始后进行使用。

def initialize_weights(model):for m in model.modules():# 判断是否属于Conv2dif isinstance(m, nn.Conv2d):torch.nn.init.zeros_(m.weight.data)# 判断是否有偏置if m.bias is not None:torch.nn.init.constant_(m.bias.data,0.3)elif isinstance(m, nn.Linear):torch.nn.init.normal_(m.weight.data, 0.1)if m.bias is not None:torch.nn.init.zeros_(m.bias.data)elif isinstance(m, nn.BatchNorm2d):m.weight.data.fill_(1) 		 m.bias.data.zeros_()	

这段代码流程是遍历当前模型的每一层，然后判断各层属于什么类型，然后根据不同类型层，设定不同的权值初始化方法。我们可以通过下面的例程进行一个简短的演示：

# 模型的定义
class MLP(nn.Module):# 声明带有模型参数的层，这里声明了两个全连接层def __init__(self, **kwargs):# 调用MLP父类Block的构造函数来进行必要的初始化。这样在构造实例时还可以指定其他函数super(MLP, self).__init__(**kwargs)self.hidden = nn.Conv2d(1,1,3)self.act = nn.ReLU()self.output = nn.Linear(10,1)# 定义模型的前向计算，即如何根据输入x计算返回所需要的模型输出def forward(self, x):o = self.act(self.hidden(x))return self.output(o)mlp = MLP()
print(mlp.hidden.weight.data)
print("-------初始化-------")mlp.apply(initialize_weights)
# 或者initialize_weights(mlp)
print(mlp.hidden.weight.dat

注意： 我们在初始化时，最好不要将模型的参数初始化为0，因为这样会导致梯度消失，从而影响模型的训练效果。因此，我们在初始化时，可以使用其他初始化方法或者将模型初始化为一个很小的值，如0.01，0.1等。

---

2.损失函数

在深度学习广为使用的今天，我们可以在脑海里清晰的知道，一个模型想要达到很好的效果需要学习，也就是我们常说的训练。一个好的训练离不开优质的负反馈，这里的损失函数就是模型的负反馈。

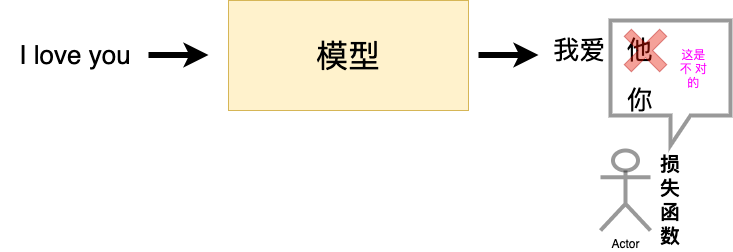
所以在PyTorch中，损失函数是必不可少的。它是数据输入到模型当中，产生的结果与真实标签的评价指标，我们的模型可以按照损失函数的目标来做出改进。

下面我们将开始探索PyTorch的所拥有的损失函数。这里将列出PyTorch中常用的损失函数（一般通过torch.nn调用），并详细介绍每个损失函数的功能介绍、数学公式和调用代码。当然，PyTorch的损失函数还远不止这些，在解决实际问题的过程中需要进一步探索、借鉴现有工作，或者设计自己的损失函数。

经过本节的学习，你将收获：

• 在深度学习中常见的损失函数及其定义方式

• PyTorch中损失函数的调用

2.1.二分类交叉熵损失

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')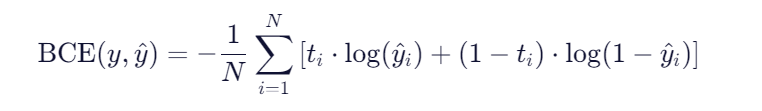

计算预测值和真实值的一个差距.

功能：计算二分类任务时的交叉熵（Cross Entropy）函数。在二分类中，label是{0,1}。对于进入交叉熵函数的input为概率分布的形式。一般来说，input为sigmoid激活层的输出，或者softmax的输出。

参数名	类型	说明
weight	Tensor 或 None	一个手动重新缩放每个批次元素损失的张量。它通常是一个包含每个类别权重的 1D 张量，用于处理类别不平衡问题。如果指定，必须是 Tensor 类型。
size_average	bool	已弃用。指定是否对输出进行平均。如果 True，则损失将对 batch size 求平均。
reduce	bool	已弃用。指定是否将输出根据 size_average 进行归约（reduction）。
reduction	str	指定应用于输出的归约方式。可选值为：'none'：不进行归约，返回原始 loss；'mean'：返回所有 loss 的平均值；'sum'：返回所有 loss 的总和。此参数取代了已弃用的 size_average 和 reduce。

import torch
import torch.nn as nnm = nn.Sigmoid()
loss = nn.BCELoss()input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)output = loss(m(input), target)
print(output)
print(output.backward())

2.2.交叉熵损失函数

torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')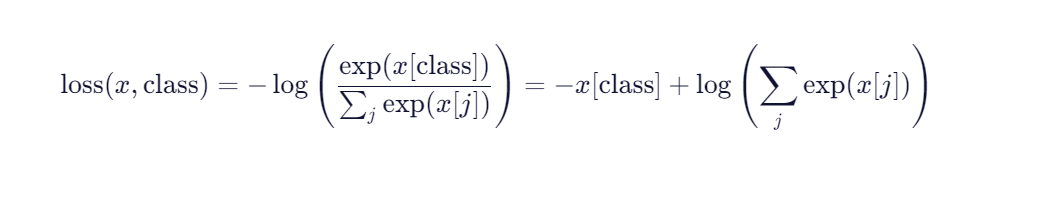

参数名	类型	默认值	说明
weight	Tensor 或 None	None	手动赋予每个类别的权重，形状为 (C,)。常用于处理类别不平衡问题。例如：weight=torch.tensor([1.0, 2.0, 1.0]) 给第2类更高权重。
ignore_index	int	-100	指定一个目标值，该值对应的 loss 不参与梯度计算且不影响平均。常用于忽略 padding 或无效标签（如语义分割中的“背景”或 NLP 中的 <pad>）。
reduction	str	'mean'	损失的归约方式： • 'none'：不归约，返回每个样本的 loss（形状 (N,)） • 'mean'：返回所有非忽略样本 loss 的平均值 • 'sum'：返回所有非忽略样本 loss 的总和
label_smoothing	float	0.0	标签平滑系数，范围 [0, 1]。用于防止模型对预测过于自信，提升泛化能力。当 α > 0 时，真实标签概率从 1 变为 1-α，其余类别均匀分配 α/(C-1)。

import torch
import torch.nn as nn# 定义损失函数
criterion = nn.CrossEntropyLoss()# 假设 batch_size=2, num_classes=3
logits = torch.randn(2, 3, requires_grad=True)
# 示例 logits: tensor([[ 1.2, -0.5,  0.3],
#                      [-0.8,  1.0,  0.6]])target = torch.tensor([0, 2])  # 真实类别：第一个样本属于类0，第二个属于类2# 计算损失
loss = criterion(logits, target)
print("Loss:", loss.item())# 反向传播
loss.backward()
print("Gradient on logits:\n", logits.grad)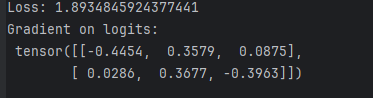

2.3.其他损失函数

损失函数名称	类名	功能描述	计算公式（简化）
L1 损失	nn.L1Loss()	计算预测值与真实值之间绝对误差
MSE 损失	nn.MSELoss()	计算预测值与真实值之间平方误差
平滑 L1 损失	nn.SmoothL1Loss(beta=1.0)	L1 的平滑版本，对离群点更鲁棒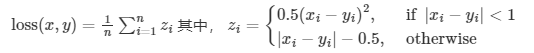
泊松负对数似然损失	nn.PoissonNLLLoss(log_input=True, full=False, eps=1e-8)	用于泊松分布回归任务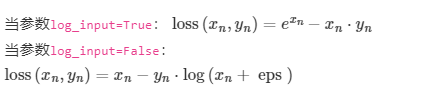
KL 散度损失	nn.KLDivLoss(log_target=False)	衡量两个概率分布之间的相对熵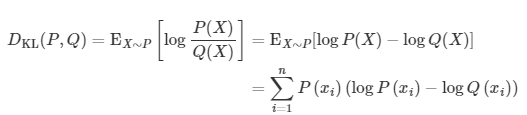
Margin Ranking Loss	nn.MarginRankingLoss(margin=0.0)	用于排序任务，衡量两样本相似性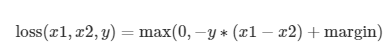
多标签边界损失	nn.MultiLabelMarginLoss()	多标签分类任务中的 Hinge 损失
二分类 Soft Margin 损失	nn.SoftMarginLoss()	二分类 logistic 损失，基于 sigmoid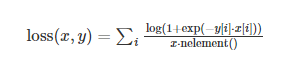
多分类折页损失	nn.MultiMarginLoss(p=1, margin=1.0, weight=None)	多分类 hinge loss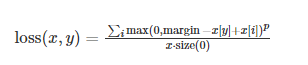
三元组损失	nn.TripletMarginLoss(margin=1.0, p=2)	学习样本间距离度量（anchor, positive, negative）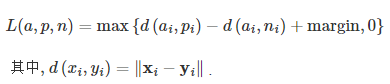
Hinge Embedding Loss	nn.HingeEmbeddingLoss(margin=1.0)	对嵌入向量进行 hinge 损失计算	输入x应为两个输入之差的绝对值
余弦相似度损失	nn.CosineEmbeddingLoss(margin=0.0)	基于余弦距离衡量两个向量相似性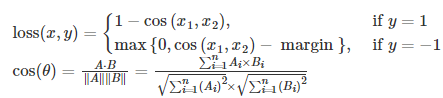
CTC 损失	nn.CTCLoss(blank=0, zero_infinity=False)	用于时序数据（如语音、OCR），处理输入输出对齐问题	对输入和目标的可能排列的概率进行求和，产生一个损失值，这个损失值对每个输入节点来说是可分的

---

3.训练与验证

我们在完成了模型的训练后，需要在测试集/验证集上完成模型的验证，以确保我们的模型具有泛化能力、不会出现过拟合等问题。在PyTorch中，训练和评估的流程是一致的，只是在训练过程中需要将模型的参数进行更新，而在评估过程中则不需要更新参数。

经过本节的学习，你将收获：

• PyTorch的训练/评估模式的开启

• 完整的训练/评估流程

完成了上述设定后就可以加载数据开始训练模型了。首先应该设置模型的状态：如果是训练状态，那么模型的参数应该支持反向传播的修改；如果是验证/测试状态，则不应该修改模型参数。在PyTorch中，模型的状态设置非常简便，如下的两个操作二选一即可：

model.train()   # 训练状态
model.eval()   # 验证/测试状态

3.1.训练

一个完整的图像分类的训练过程如下所示：

def train(epoch):# 将模型设置为训练模式，启用 BatchNorm 和 Dropout 等训练专用层model.train()# 初始化当前轮次的总损失为0train_loss = 0# 遍历训练数据加载器，获取每个批次的数据和对应标签for data, label in train_loader:# 将输入数据和标签移动到GPU上进行加速计算data, label = data.cuda(), label.cuda()# 清空优化器中上一步的梯度信息，避免梯度累积optimizer.zero_grad()# 前向传播：将数据输入模型，得到输出结果output = model(data)# 计算当前批次输出与真实标签之间的损失值loss = criterion(output, label)# 反向传播：计算梯度loss.backward()# 更新模型参数optimizer.step()# 累加当前批次的损失值（乘以样本数量，用于后续计算平均损失）train_loss += loss.item() * data.size(0)# 计算整个训练集上的平均损失train_loss = train_loss / len(train_loader.dataset)# 打印当前轮次和训练损失，保留6位小数print('Epoch: {} \tTraining Loss: {:.6f}'.format(epoch, train_loss))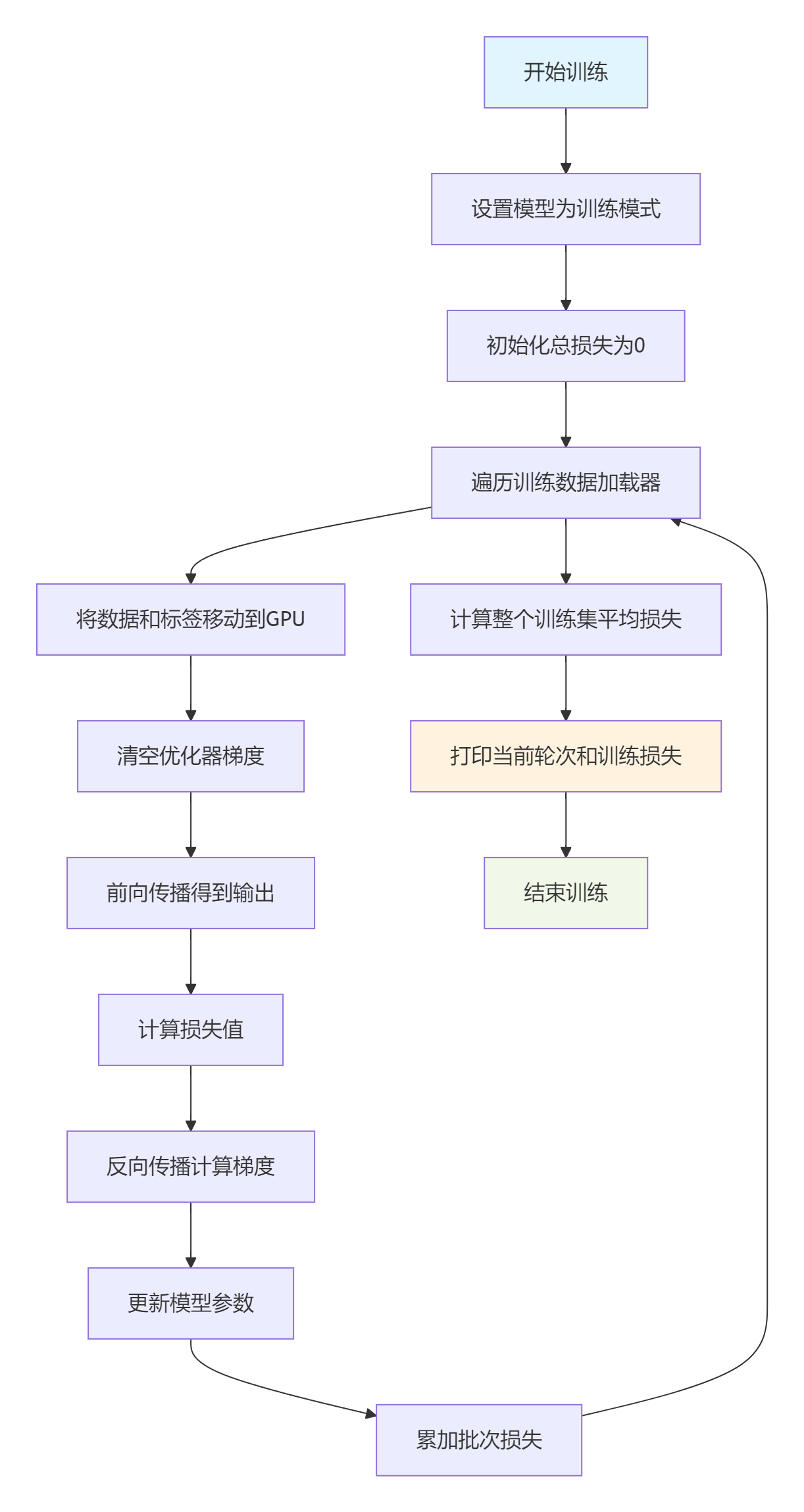

3.2.验证

对应的，一个完整图像分类的验证过程如下所示：

def val(epoch):       # 将模型设置为评估模式（关闭 Dropout、BatchNorm 等的训练行为）model.eval()# 初始化验证阶段的总损失为 0val_loss = 0# 使用 torch.no_grad() 上下文管理器，禁用梯度计算，节省内存并加快推理速度with torch.no_grad():# 遍历验证数据加载器（val_loader），获取每个批次的数据和标签for data, label in val_loader:# 将输入数据和标签移动到 GPU 上（如果可用）data, label = data.cuda(), label.cuda()# 将数据输入模型，得到输出（通常是类别 logits）output = model(data)# 对输出取每一行最大值的索引，得到预测的类别标签preds = torch.argmax(output, 1)# 计算当前批次的损失值loss = criterion(output, label)# 累加当前批次的损失值（乘以该批次样本数量，用于后续计算平均损失）val_loss += loss.item() * data.size(0)# 累加正确预测的数量（注意：这里变量 running_accu 未定义，应为错误！）# 正确写法应是先定义 running_accu = 0，或使用其他变量如 running_correctsrunning_accu += torch.sum(preds == label.data)# 计算整个验证集上的平均损失：总损失 / 验证集样本总数val_loss = val_loss / len(val_loader.dataset)# 打印当前 epoch 的验证损失（注意：这里写的是 "Training Loss"，应为笔误）# 建议改为 "Validation Loss"print('Epoch: {} \tTraining Loss: {:.6f}'.format(epoch, val_loss))

对于图像分类任务，我们还可以使用sklearn.metrics中的classification_report函数来计算模型的准确率、召回率、F1值等指标，如下所示：

from sklearn.metrics import classification_report
"""
将下方代码的labels和preds替换为模型预测出来的所有label和preds，
target_names替换为类别名称，
既可得到模型的分类报告
"""
print(classification_report(labels.cpu(), preds.cpu(), target_names=class_names))

除此之外，我们还可以使用torcheval或torchmetric来对模型进行评估。

4.优化算法

深度学习的目标是通过不断改变网络参数，使得参数能够对输入做各种非线性变换拟合输出，本质上就是一个函数去寻找最优解，只不过这个最优解是一个矩阵，而如何快速求得这个最优解是深度学习研究的一个重点，以经典的resnet-50为例，它大约有2000万个系数需要进行计算，那么我们如何计算出这么多系数，有以下两种方法：

1. 第一种是直接暴力穷举一遍参数，这种方法从理论上行得通，但是实施上可能性基本为0，因为参数量过于庞大。

2. 为了使求解参数过程更快，人们提出了第二种办法，即BP+优化器逼近求解。

因此，优化器是根据网络反向传播的梯度信息来更新网络的参数，以起到降低loss函数计算值，使得模型输出更加接近真实标签。

经过本节的学习，你将收获：

• 了解PyTorch的优化器

• 学会使用PyTorch提供的优化器进行优化

• 优化器的属性和构造

• 优化器的对比

也就是找到损失最小，准确率最高，一般都是前向传播+反向传播+优化算法

PyTorch很人性化的给我们提供了一个优化器的库torch.optim，在这里面提供了多种优化器。

• torch.optim.SGD

• torch.optim.ASGD

• torch.optim.Adadelta

• torch.optim.Adagrad

• torch.optim.Adam

• torch.optim.AdamW

• torch.optim.Adamax

• torch.optim.RAdam

• torch.optim.NAdam

• torch.optim.SparseAdam

• torch.optim.LBFGS

• torch.optim.RMSprop

• torch.optim.Rprop

以上这些优化算法均继承于Optimizer，下面我们先来看下所有优化器的基类Optimizer。定义如下：

class Optimizer(object):def __init__(self, params, defaults):        self.defaults = defaultsself.state = defaultdict(dict)self.param_groups = []

4.1.Optimizer属性

名称	类型	描述
param_groups	list of dict	存储优化器管理的参数组列表。每个参数组是一个字典，包含 'params'（参数列表）和其他超参数（如 lr, momentum 等）。这是与参数交互的核心结构。
state	dict	存储每个参数的状态信息（如动量缓冲区、历史梯度等）。键通常是参数对象（Parameter），值是包含状态张量的字典。不同优化器（如 Adam、SGD）在此存储不同的状态变量。
defaults	dict	存储优化器的默认超参数。在初始化参数组时，未指定的超参数会从 defaults 中获取。 {'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}

4.2.Optimizer方法

__init__(self, params, defaults)	构造函数	初始化优化器。输入 params（可迭代的 Parameter 对象或参数组），并设置 defaults。负责构建 param_groups 和初始化 state。
zero_grad(set_to_none=False)	方法	将所有被管理参数的梯度置零。set_to_none=True 时将 grad 属性设为 None（节省内存，推荐使用）。
step(closure=None)	抽象方法	核心优化步骤。执行一次参数更新。closure 是一个可选的无参函数，用于重新计算损失（在需要重新前向传播的场景，如 L-BFGS 中使用）。子类必须实现此方法。
add_param_group(param_group)	方法	向优化器动态添加一个新的参数组 param_group（字典，包含 'params' 和超参数）。用于在训练中为新层或不同超参数的层添加优化。
state_dict()	方法	返回优化器的状态字典，包含 state 和 param_groups。用于保存优化器状态（如检查点）。
load_state_dict(state_dict)	方法	从 state_dict() 返回的字典加载优化器状态。确保模型结构和参数未改变，否则可能出错。

其他方法：

__getstate__()	魔法方法	定义对象被 pickle 序列化时的行为。通常用于支持 torch.save。
__setstate__(state)	魔法方法	定义对象被 pickle 反序列化时的行为。通常用于支持 torch.load。
__repr__()	魔法方法	返回优化器的字符串表示，便于调试和打印。
share_memory()	方法	（较少使用）将优化器状态张量移动到共享内存，支持多进程训练。
__class__, __dict__ 等	内置属性	Python 对象的标准属性，用于反射和元编程。

import os
import torch# 设置权重：创建一个 2x2 的张量，从标准正态分布中采样，并开启梯度追踪
weight = torch.randn((2, 2), requires_grad=True)# 手动设置梯度：将 weight 的梯度设为全 1 的 2x2 矩阵
weight.grad = torch.ones((2, 2))# 输出更新前的权重数据和梯度
print("更新前的权重数据（weight.data）:\n{}".format(weight.data))
print("当前梯度（weight.grad）:\n{}".format(weight.grad))# 实例化 SGD 优化器
# 传入参数列表 [weight]，设置学习率 lr=0.1，动量 momentum=0.9
optimizer = torch.optim.SGD([weight], lr=0.1, momentum=0.9)# 执行一步优化：根据当前梯度和动量更新参数
optimizer.step()# 查看执行 step 后的权重数据和梯度（注意：step 不会清空 grad）
print("执行 optimizer.step() 后的权重数据（weight.data）:\n{}".format(weight.data))
print("梯度仍未清零（weight.grad）:\n{}".format(weight.grad))# 清零梯度：将所有被优化器管理的参数的梯度置为零（或 None）
optimizer.zero_grad()# 检查梯度是否已清零
print("执行 optimizer.zero_grad() 后的梯度（应为全 0）:\n{}".format(weight.grad))# 输出优化器的参数组信息（param_groups）
# 包含学习率、动量等超参数及参数列表
print("optimizer.param_groups 是:\n{}".format(optimizer.param_groups))# 检查 weight 是否是同一个对象（通过内存地址 id 判断）
# 输出优化器内部保存的参数与原始 weight 的内存地址
print("优化器中的 weight 地址: {}".format(id(optimizer.param_groups[0]['params'][0])))
print("外部定义的 weight 地址: {}".format(id(weight)))
print("两者是否为同一对象: {}".format(id(optimizer.param_groups[0]['params'][0]) == id(weight)))
print("说明：优化器直接引用原始参数，而非复制，因此共享同一内存对象。\n")# 新增第二个参数 weight2
weight2 = torch.randn((3, 3), requires_grad=True)# 向优化器动态添加新的参数组
# 设置该组的学习率更低（lr=0.0001），并启用 Nesterov 动量
optimizer.add_param_group({"params": weight2, 'lr': 0.0001, 'nesterov': True})# 查看添加新参数后的 param_groups
print("添加 weight2 后的 optimizer.param_groups 是:\n{}".format(optimizer.param_groups))# 获取优化器当前的状态字典（包含 param_groups 和 state）
opt_state_dict = optimizer.state_dict()
print("调用 step 前的 state_dict:\n", opt_state_dict)# 连续执行 50 次优化步骤（模拟训练过程）
# 注意：由于没有真实损失函数和反向传播，梯度仍保持为初始值或未更新
# 实际中应在每次 step 前进行 loss.backward() 和 zero_grad()
for _ in range(50):optimizer.step()# 查看多次更新后的状态字典（动量状态已被累积更新）
print("执行 50 次 step 后的 state_dict:\n", optimizer.state_dict())# 保存优化器状态到本地文件
save_path = os.path.join(r"D:\pythonProject\深度学习\pytorch\基础学习\优化器", "optimizer_state_dict.pkl")
torch.save(optimizer.state_dict(), save_path)
print("✅ 优化器状态已保存至：", save_path)# 加载之前保存的优化器状态
loaded_state_dict = torch.load(save_path)
optimizer.load_state_dict(loaded_state_dict)
print("✅ 成功加载优化器状态")
print("加载的状态字典内容:\n", loaded_state_dict)# 最后输出优化器的关键属性信息# defaults: 优化器的默认超参数配置
print("\n--- optimizer.defaults（默认超参数）---")
print(optimizer.defaults)# state: 存储每个参数的优化状态（如动量缓冲区）
print("\n--- optimizer.state（参数状态缓存）---")
print(optimizer.state)
# 提示：state 的键是参数对象，值是状态字典（如 'momentum_buffer'）# param_groups: 当前所有参数组的配置
print("\n--- optimizer.param_groups（参数组配置）---")
print(optimizer.param_groups)print("\n🎉 程序执行完毕")