数字信号 · 时域变换 | 时移、伸缩与反转及 MATLAB 实现
注:本文为 “数字信号 · 时域变换” 相关合辑。
英文引文,机翻未校。
中文引文,略作重排。
如有内容异常,请看原文。
Time Shifting, Time Scaling & Time Reversal of Signals
信号的时间平移、时间伸缩与时间反转
September 14, 2019 by Electricalvoice
In signal processing, a signal undergoes several manipulations of its independent variable, i.e., time. Based on this, we can classify such operations as follows:
在信号处理领域,信号的独立变量(即时间)会经历多种运算操作。基于此,我们可将这类操作分类为:
- Time Shifting
时间平移 - Time Scaling
时间伸缩 - Time Reversal
时间反转
These are operations corresponding to the transformation of the independent variable (time).
上述均为与独立变量(时间)变换相关的操作。
Let us analyze each operation one by one.
下面我们逐一分析每种操作。
Time Shifting
时间平移
A signal x(t)x(t)x(t) can be shifted in time by replacing the independent variable ttt with either t−t0t - t_0t−t0 or t+t0t + t_0t+t0. Here, t0t_0t0 is referred to as the shifting factor. Time shifting may result in a time delay or a time advancement of the signal.
将信号 x(t)x(t)x(t) 的独立变量 ttt 替换为 t−t0t - t_0t−t0 或 t+t0t + t_0t+t0,即可实现信号的时间平移。其中,t0t_0t0 被称为平移因子。时间平移可能使信号产生时间延迟或时间提前。
If the independent variable ttt is replaced by t−t0t - t_0t−t0, the signal is shifted to the right, and this time shift causes a delay of the signal by t0t_0t0 time units. This type of time shifting is known as right-side shifting. It can be achieved by adding the value of t0t_0t0 to each time instant of the signal x(t)x(t)x(t).
若将独立变量 ttt 替换为 t−t0t - t_0t−t0,信号会向右平移,且该平移会使信号延迟 t0t_0t0 个时间单位。这类时间平移被称为右侧平移。对信号 x(t)x(t)x(t) 的每个时间点均加上 t0t_0t0 的值,即可实现右侧平移。
Consider a signal x(t)x(t)x(t) as shown in Figure 1(i). Figure 1(ii) shows the signal x(t−4)x(t - 4)x(t−4). During this process, the width of the signal x(t)x(t)x(t) remains unchanged. Therefore, W=W0W = W_0W=W0.
观察图1(i)所示的信号 x(t)x(t)x(t),图1(ii)为信号 x(t−4)x(t - 4)x(t−4) 的波形。在此过程中,信号 x(t)x(t)x(t) 的宽度保持不变,因此有 W=W0W = W_0W=W0。
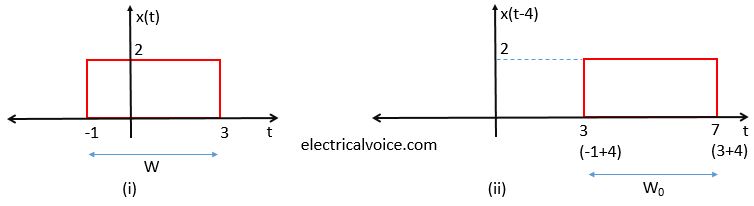
Fig. 1 Right-side time shifting (signal delay)
图1 右侧时间平移(信号延迟)
If the independent variable ttt is replaced by t+t0t + t_0t+t0, the signal is shifted to the left, and this time shift causes an advancement of the signal by t0t_0t0 time units. This type of time shifting is known as left-side shifting. It can be achieved by subtracting the value of t0t_0t0 from each time instant of the signal x(t)x(t)x(t).
若将独立变量 ttt 替换为 t+t0t + t_0t+t0,信号会向左平移,且该平移会使信号提前 t0t_0t0 个时间单位。这类时间平移被称为左侧平移。对信号 x(t)x(t)x(t) 的每个时间点均减去 t0t_0t0 的值,即可实现左侧平移。
Consider a signal x(t)x(t)x(t) as shown in Figure 2(i). Figure 2(ii) shows the signal x(t+2)x(t + 2)x(t+2). During this process, the width of the signal x(t)x(t)x(t) remains unchanged. Therefore, W=W0W = W_0W=W0.
观察图2(i)所示的信号 x(t)x(t)x(t),图2(ii)为信号 x(t+2)x(t + 2)x(t+2) 的波形。在此过程中,信号 x(t)x(t)x(t) 的宽度保持不变,因此有 W=W0W = W_0W=W0。
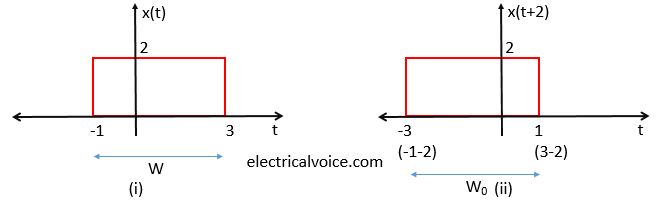
Fig. 2 Left-side time shifting (signal advancement)
图2 左侧时间平移(信号提前)
Time Scaling
时间伸缩
A signal x(t)x(t)x(t) can be scaled in time by replacing the independent variable ttt with atatat. Here, aaa is referred to as the scaling factor. Time scaling may result in compression or expansion of the signal.
将信号 x(t)x(t)x(t) 的独立变量 ttt 替换为 atatat,即可实现信号的时间伸缩。其中,aaa 被称为伸缩因子。时间伸缩可能使信号产生压缩或扩展。
If the independent variable ttt is replaced by atatat and a>1a > 1a>1, the signal is compressed. This can be achieved by dividing each time instant of the signal x(t)x(t)x(t) by aaa.
若将独立变量 ttt 替换为 atatat 且满足 a>1a > 1a>1,信号会被压缩。对信号 x(t)x(t)x(t) 的每个时间点均除以 aaa 的值,即可实现信号压缩。
If the independent variable ttt is replaced by atatat and 0<a<10 < a < 10<a<1, the signal is expanded. This can be achieved by dividing each time instant of the signal x(t)x(t)x(t) by aaa.
若将独立变量 ttt 替换为 atatat 且满足 0<a<10 < a < 10<a<1,信号会被扩展。对信号 x(t)x(t)x(t) 的每个时间点均除以 aaa 的值,即可实现信号扩展。
Consider a signal x(t)x(t)x(t) as shown in Figure 3(i). Figure 3(ii) shows the signal x(3t)x(3t)x(3t). Since a>1a > 1a>1, the signal is compressed. During this process, the width of the signal x(t)x(t)x(t) changes; therefore, W<W0W < W_0W<W0 . Figure 3(iii) shows the signal x(12.5t)x\left(\frac{1}{2.5}t\right)x(2.51t). Since 0<a<10 < a < 10<a<1, the signal is expanded. During this process, the width of the signal x(t)x(t)x(t) changes; therefore, W>W0W > W_0W>W0 .
观察图3(i)所示的信号 x(t)x(t)x(t),图3(ii)为信号 x(3t)x(3t)x(3t) 的波形。由于 a=3>1a = 3 > 1a=3>1,该信号呈压缩状态。在此过程中,信号 x(t)x(t)x(t) 的宽度发生变化,因此有 W<W0W < W_0W<W0(注:压缩后的信号宽度小于原信号宽度)。图3(iii)为信号 x(12.5t)x\left(\frac{1}{2.5}t\right)x(2.51t) 的波形。由于 0<a=12.5<10 < a = \frac{1}{2.5} < 10<a=2.51<1,该信号呈扩展状态。在此过程中,信号 x(t)x(t)x(t) 的宽度发生变化,因此有 W>W0W > W_0W>W0(注:扩展后的信号宽度大于原信号宽度)。
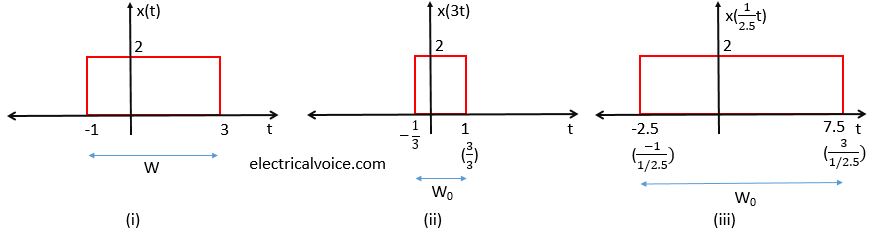
Fig. 3 Time scaling of a signal
图3 信号的时间伸缩
Time Reversal
时间反转
If the independent variable ttt is replaced by −t-t−t, this operation is known as time reversal of the signal with respect to the y-axis (or amplitude axis). It can be achieved by taking the mirror image of the signal x(t)x(t)x(t) about the y-axis or by rotating x(t)x(t)x(t) 180° around the y-axis. Hence, time reversal is also referred to as folding or reflection.
将信号的独立变量 ttt 替换为 −t-t−t,这类操作被称为信号关于y轴(或幅度轴)的时间反转。对信号 x(t)x(t)x(t) 取关于 y 轴的镜像,或使 x(t)x(t)x(t) 绕y轴旋转180°,均可实现时间反转。因此,时间反转也被称为折叠或反射。
Consider a signal x(t)x(t)x(t) as shown in Figure 4(i). The time reversal of this signal can be obtained by taking its mirror image about the y-axis, as shown in Figure 4(ii). During this process, the width of the signal x(t)x(t)x(t) remains unchanged. Therefore, W=W0W = W_0W=W0.
观察图4(i)所示的信号 x(t)x(t)x(t),对其取关于 y 轴的镜像(如图4(ii)所示),即可得到该信号的时间反转波形。在此过程中,信号 x(t)x(t)x(t) 的宽度保持不变,因此有 W=W0W = W_0W=W0。
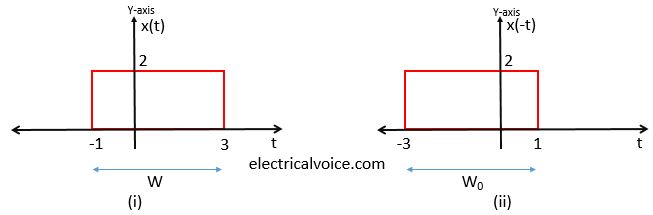
Fig. 4 Time reversal (or folding) of a signal
图4 信号的时间反转(或折叠)
信号处理中时间平移(延时/超前)
1 引言
在数字信号处理(Digital Signal Processing, DSP)中,序列的时间平移(包括延时与超前)是最基础的信号变换操作之一,广泛应用于滤波器设计、信号同步、系统因果性分析等场景。然而,由于时间平移涉及“原序列”与“变换后序列”的关联,初学者常对表达式中“+t+t+t”与“−t-t−t”对应的物理意义产生混淆(即“延时应取‘加’还是‘减’”)。
本文将从数学定义出发,结合离散时间序列与连续时间信号的实例,推导时间平移的数学表达与物理意义的对应关系,明确“延时”与“超前”的判断准则,避免死记硬背导致的概念混淆。
2 基本定义
时间平移的核心是“信号在时间轴上的位置移动”,需先明确两个关键对象:
- 原信号:记为离散时间序列 x[n]x[n]x[n](或连续时间信号 x(t)x(t)x(t)),其自变量 nnn(或 ttt)表示时间索引(或连续时间);
- 平移后信号:记为离散时间序列 y[n]y[n]y[n](或连续时间信号 y(t)y(t)y(t)),是原信号 x[⋅]x[\cdot]x[⋅] 经过时间平移后得到的新信号。
时间平移的数学表达式可统一表示为:
- 离散时间域:y[n]=x[n−k]y[n] = x[n - k]y[n]=x[n−k] 或 y[n]=x[n+k]y[n] = x[n + k]y[n]=x[n+k](其中 k∈Z+k \in \mathbb{Z}^+k∈Z+,即 kkk 为正整数,此处 kkk 仅表示平移的量值,不带方向);
- 连续时间域:y(t)=x(t−τ)y(t) = x(t - \tau)y(t)=x(t−τ) 或 y(t)=x(t+τ)y(t) = x(t + \tau)y(t)=x(t+τ)(其中 τ∈R+\tau \in \mathbb{R}^+τ∈R+,即 τ\tauτ 为正实数,此处 τ\tauτ 仅表示平移的量值,不带方向)。
下文将分别以离散时间序列(更易通过数值验证)和连续时间信号为例,分析“−k-k−k(或 −τ-\tau−τ)”与“+k+k+k(或 +τ+\tau+τ)”对应的物理意义。
3 离散时间序列的时间平移分析
离散时间序列的自变量 nnn 为整数(如 n=…,−2,−1,0,1,2,…n = \dots, -2, -1, 0, 1, 2, \dotsn=…,−2,−1,0,1,2,…),可通过“代入具体时间索引,对比原序列与平移后序列的取值”直观推导平移方向。
例 1:y[n]=x[n−k]y[n] = x[n - k]y[n]=x[n−k](k>0k > 0k>0)
设原序列 x[n]x[n]x[n] 的取值如下(仅列举关键时间点):
| nnn | …\dots… | −1-1−1 | 000 | 111 | 222 | 333 | …\dots… |
|---|---|---|---|---|---|---|---|
| x[n]x[n]x[n] | …\dots… | x[−1]x[-1]x[−1] | x[0]x[0]x[0] | x[1]x[1]x[1] | x[2]x[2]x[2] | x[3]x[3]x[3] | …\dots… |
根据 y[n]=x[n−k]y[n] = x[n - k]y[n]=x[n−k],计算平移后序列 y[n]y[n]y[n] 在相同时间索引 nnn 处的取值:
- 当 n=0n = 0n=0 时:y[0]=x[0−k]=x[−k]y[0] = x[0 - k] = x[-k]y[0]=x[0−k]=x[−k];
- 当 n=kn = kn=k 时:y[k]=x[k−k]=x[0]y[k] = x[k - k] = x[0]y[k]=x[k−k]=x[0];
- 当 n=k+1n = k + 1n=k+1 时:y[k+1]=x[(k+1)−k]=x[1]y[k + 1] = x[(k + 1) - k] = x[1]y[k+1]=x[(k+1)−k]=x[1];
- 当 n=k+2n = k + 2n=k+2 时:y[k+2]=x[(k+2)−k]=x[2]y[k + 2] = x[(k + 2) - k] = x[2]y[k+2]=x[(k+2)−k]=x[2];
- 以此类推,对任意 nnn,有 y[n]=x[n−k]⟹y[n+k]=x[n]y[n] = x[n - k] \implies y[n + k] = x[n]y[n]=x[n−k]⟹y[n+k]=x[n]。
推导:
原序列 x[n]x[n]x[n] 在 n=0n = 0n=0 处的取值 x[0]x[0]x[0],出现在平移后序列 y[n]y[n]y[n] 的 n=kn = kn=k 处;
原序列 x[n]x[n]x[n] 在 n=1n = 1n=1 处的取值 x[1]x[1]x[1],出现在平移后序列 y[n]y[n]y[n] 的 n=k+1n = k + 1n=k+1 处。
这表明:y[n]y[n]y[n] 的所有取值,均比 x[n]x[n]x[n] 晚 kkk 个时间单位出现,即 y[n]y[n]y[n] 是 x[n]x[n]x[n] 经过 延时 kkk 个单位 后的序列,且序列波形沿 nnn 轴(时间轴)向右平移 kkk 个单位。
例 2:y[n]=x[n+k]y[n] = x[n + k]y[n]=x[n+k](k>0k > 0k>0)
同样基于表3.1中 x[n]x[n]x[n] 的取值,计算 y[n]=x[n+k]y[n] = x[n + k]y[n]=x[n+k] 的取值:
- 当 n=−kn = -kn=−k 时:y[−k]=x[−k+k]=x[0]y[-k] = x[-k + k] = x[0]y[−k]=x[−k+k]=x[0];
- 当 n=−k+1n = -k + 1n=−k+1 时:y[−k+1]=x[(−k+1)+k]=x[1]y[-k + 1] = x[(-k + 1) + k] = x[1]y[−k+1]=x[(−k+1)+k]=x[1];
- 当 n=0n = 0n=0 时:y[0]=x[0+k]=x[k]y[0] = x[0 + k] = x[k]y[0]=x[0+k]=x[k];
- 以此类推,对任意 nnn,有 y[n]=x[n+k]⟹y[n−k]=x[n]y[n] = x[n + k] \implies y[n - k] = x[n]y[n]=x[n+k]⟹y[n−k]=x[n]。
推导:
原序列 x[n]x[n]x[n] 在 n=0n = 0n=0 处的取值 x[0]x[0]x[0],出现在平移后序列 y[n]y[n]y[n] 的 n=−kn = -kn=−k 处;
原序列 x[n]x[n]x[n] 在 n=1n = 1n=1 处的取值 x[1]x[1]x[1],出现在平移后序列 y[n]y[n]y[n] 的 n=−k+1n = -k + 1n=−k+1 处。
这表明:y[n]y[n]y[n] 的所有取值,均比 x[n]x[n]x[n] 早 kkk 个时间单位出现,即 y[n]y[n]y[n] 是 x[n]x[n]x[n] 经过 超前 kkk 个单位 后的序列,且序列波形沿 nnn 轴(时间轴)向左平移 kkk 个单位。
4 连续时间信号的时间平移验证
连续时间信号的自变量 ttt 为实数,其时间平移的逻辑与离散时间序列一致,可通过“信号波形的位置关系”验证。
4.1 数学表达与物理意义
设连续时间原信号为 x(t)x(t)x(t),平移后信号为 y(t)y(t)y(t),则:
-
若 y(t)=x(t−τ)y(t) = x(t - \tau)y(t)=x(t−τ)(τ>0\tau > 0τ>0):
对任意时刻 t0t_0t0,y(t0)=x(t0−τ)y(t_0) = x(t_0 - \tau)y(t0)=x(t0−τ),即 y(t)y(t)y(t) 在 t0t_0t0 处的取值,等于 x(t)x(t)x(t) 在 t0−τt_0 - \taut0−τ 处的取值。
物理意义:x(t)x(t)x(t) 的波形沿 ttt 轴向右平移 τ\tauτ 个单位,y(t)y(t)y(t) 相对于 x(t)x(t)x(t) 延时 τ\tauτ 个单位。 -
若 y(t)=x(t+τ)y(t) = x(t + \tau)y(t)=x(t+τ)(τ>0\tau > 0τ>0):
对任意时刻 t0t_0t0,y(t0)=x(t0+τ)y(t_0) = x(t_0 + \tau)y(t0)=x(t0+τ),即 y(t)y(t)y(t) 在 t0t_0t0 处的取值,等于 x(t)x(t)x(t) 在 t0+τt_0 + \taut0+τ 处的取值。
物理意义:x(t)x(t)x(t) 的波形沿 ttt 轴向左平移 τ\tauτ 个单位,y(t)y(t)y(t) 相对于 x(t)x(t)x(t) 超前 τ\tauτ 个单位。
4.2 实例:矩形脉冲信号的平移
设原信号为矩形脉冲 x(t)=rect(tT)x(t) = \text{rect}\left(\frac{t}{T}\right)x(t)=rect(Tt),其中 rect(⋅)\text{rect}(\cdot)rect(⋅) 为矩形窗函数,定义为:
rect(z)={1,∣z∣<1212,∣z∣=120,∣z∣>12\text{rect}(z) = \begin{cases} 1, & |z| < \frac{1}{2} \\ \frac{1}{2}, & |z| = \frac{1}{2} \\ 0, & |z| > \frac{1}{2} \end{cases} rect(z)=⎩⎨⎧1,21,0,∣z∣<21∣z∣=21∣z∣>21
则 x(t)x(t)x(t) 的非零区间为 t∈(−T2,T2)t \in \left(-\frac{T}{2}, \frac{T}{2}\right)t∈(−2T,2T)。
-
平移后信号 y1(t)=x(t−τ)=rect(t−τT)y_1(t) = x(t - \tau) = \text{rect}\left(\frac{t - \tau}{T}\right)y1(t)=x(t−τ)=rect(Tt−τ):
非零区间变为 t−τ∈(−T2,T2)⟹t∈(τ−T2,τ+T2)t - \tau \in \left(-\frac{T}{2}, \frac{T}{2}\right) \implies t \in \left(\tau - \frac{T}{2}, \tau + \frac{T}{2}\right)t−τ∈(−2T,2T)⟹t∈(τ−2T,τ+2T),即波形向右平移 τ\tauτ,对应延时 τ\tauτ。 -
平移后信号 y2(t)=x(t+τ)=rect(t+τT)y_2(t) = x(t + \tau) = \text{rect}\left(\frac{t + \tau}{T}\right)y2(t)=x(t+τ)=rect(Tt+τ):
非零区间变为 t+τ∈(−T2,T2)⟹t∈(−τ−T2,−τ+T2)t + \tau \in \left(-\frac{T}{2}, \frac{T}{2}\right) \implies t \in \left(-\tau - \frac{T}{2}, -\tau + \frac{T}{2}\right)t+τ∈(−2T,2T)⟹t∈(−τ−2T,−τ+2T),即波形向左平移 τ\tauτ,对应超前 τ\tauτ。
5 常见误区
初学者对“加/减”与“延时/超前”的混淆,本质是忽略了“比较对象”和“自变量的物理意义”,需明确以下两点:
误区 1:孤立关注“原信号的自变量运算”
错误逻辑:认为“x[n−k]x[n - k]x[n−k] 是 x[n]x[n]x[n] 的自变量减 kkk,所以序列左移”——该逻辑孤立看待 x[⋅]x[\cdot]x[⋅] 的参数变化,未关联平移后信号 y[n]y[n]y[n]。
正确逻辑:时间平移的判断依据是“平移后信号 y[⋅]y[\cdot]y[⋅] 与原信号 x[⋅]x[\cdot]x[⋅] 在同一时间点的取值关联”(如 y[k]=x[0]y[k] = x[0]y[k]=x[0]),而非原信号自身的参数运算。
误区 2:混淆“离散时间”与“连续时间”的平移规则
部分初学者认为“离散时间序列的规则不适用于连续时间信号”,但前文推导表明:
无论是离散序列 x[n]x[n]x[n] 还是连续信号 x(t)x(t)x(t),时间平移的核心规则一致——“减正数”对应右移(延时),“加正数”对应左移(超前),仅自变量的取值范围(整数/实数)不同。
6 时间平移规则概览
数字信号处理中,时间平移的“加/减”与“延时/超前”对应关系可总结为以下核心准则,适用于离散时间序列与连续时间信号:
| 数学表达式(正参数 k,τk, \tauk,τ) | 序列/波形移动方向 | 物理意义(yyy 相对于 xxx) |
|---|---|---|
| y[n]=x[n−k]y[n] = x[n - k]y[n]=x[n−k] y(t)=x(t−τ)y(t) = x(t - \tau)y(t)=x(t−τ) | 沿时间轴向右移动 | 延时 kkk(或 τ\tauτ)个单位 |
| y[n]=x[n+k]y[n] = x[n + k]y[n]=x[n+k] y(t)=x(t+τ)y(t) = x(t + \tau)y(t)=x(t+τ) | 沿时间轴向左移动 | 超前 kkk(或 τ\tauτ)个单位 |
实际应用中,无需死记结论,可通过“代入具体时间点(离散)”或“分析非零区间(连续)”的方法快速验证,从根本上理解时间平移的数学本质与物理意义。
信号的时间平移、反转与伸缩变换
L_Ali 于 2021-09-25 21:18:45 发布
问题
如何将信号 f(t)f(t)f(t) 通过时间平移(时移)、时间反转(反转)、时间尺度变换(伸缩)转化为 f(−at+b)f(-at+b)f(−at+b)?
三种变换的执行顺序是否存在规定?
时间平移、反转与伸缩变换均是对函数自变量 ttt 的操作,不改变函数值(即信号幅度)。

三种变换的图像含义
可参考《信号与系统》(奥本海姆第二版)第 6 - 8 页以及《信号与线性系统分析》(吴大正第四版)第 9 - 11 页的解释。
三种变换的顺序可以灵活改变(图 2)
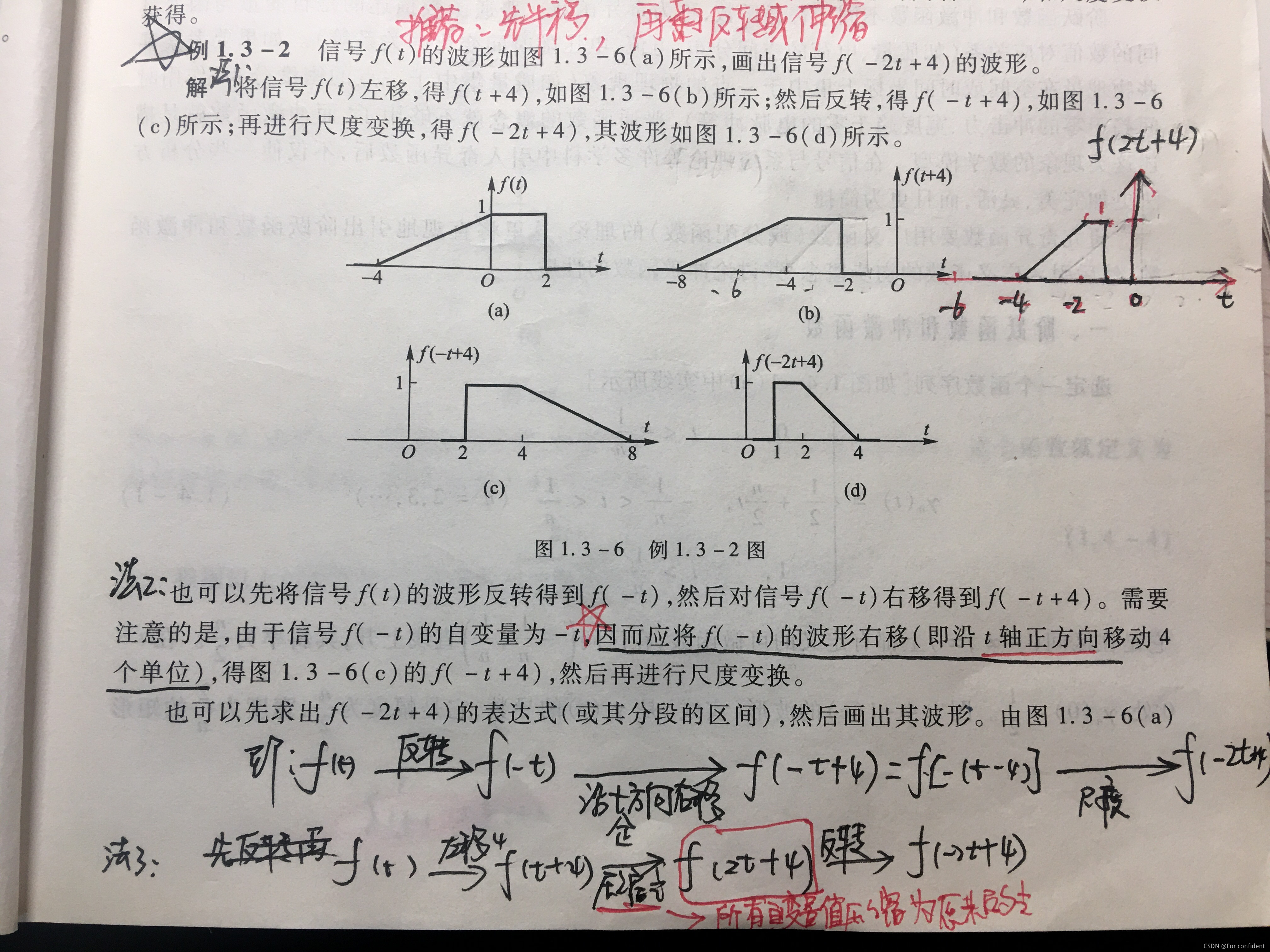
图 2:图形变换的多种顺序举例:
变换中的注意事项
- 以 f(−t+4)f(-t + 4)f(−t+4) 为例,是将 f(−t)f(-t)f(−t) 的波形沿 ttt 的正方向移动 4 个单位。
- 在伸缩变换中,所有自变量值均需进行伸缩,需注意拐角点的值。
变换顺序的推荐
推荐先进行时移,再进行伸缩,最后进行反转,此顺序不易出错。
函数表达式求解方法(图 3)

图 3:函数表达式求解图像方法
信号在 MATLAB 中的运算——信号的时移、反折和尺度变换
Oliver-H 已于 2024-04-07 11:52:17 修改
引言
本文旨在通过 MATLAB 实现离散时间序列的基本运算,掌握 MATLAB 函数的编写与调试方法,同时加深对连续时间信号时域运算的理解。
离散序列的时域运算
离散序列的时域运算包括信号的相加、相乘,以及信号的移位、反折、尺度变换等。在 MATLAB 中,离散序列的相加、相乘运算是两个向量之间的运算,因此参与运算的两个序列向量必须具有相同的维数,否则应进行相应处理。
MATLAB 代码示例
以下是利用 MATLAB 实现离散序列时移、尺度变换和反折的代码示例:
% 离散序列的时移、反折、尺度变换的实现。
clc;
clear;
close all;k = -12:12;
k1 = 2.*k+4;
f = -[stepfun(k,-3)-stepfun(k,-1)] +...4.*[stepfun(k,-1)-stepfun(k,0)] +...0.5*k.*[stepfun(k,0)-stepfun(k,11)];f1 = -[stepfun(k1,-3)-stepfun(k1,-1)] +...4.*[stepfun(k1,-1)-stepfun(k1,0)] +...0.5*k1.*[stepfun(k1,0)-stepfun(k1,11)];subplot(221); stem(k,f); axis([-12 12 -1 6]);
grid on; xlabel('n'); ylabel('h(n)');
text(-8,3,'f[k]');
title('原离散序列')subplot(222); stem(k+1,f); axis([-12 12 -1 6]);
grid on; xlabel('n'); ylabel('h(n)');
text(-9.5,3,'f[k-1]');
title('离散序列的时移')subplot(223); stem(k,f1); axis([-12 12 -1 6]);
grid on; xlabel('n'); ylabel('h(n)');
text(-8,3,'f[2k+4]');
title('离散序列的尺度变换+时移')subplot(224); stem(2-k,f); axis([-12 12 -1 6]);
grid on; xlabel('n'); ylabel('h(n)');
text(5.5,3,'f[2-k]');
title('离散序列的反折')
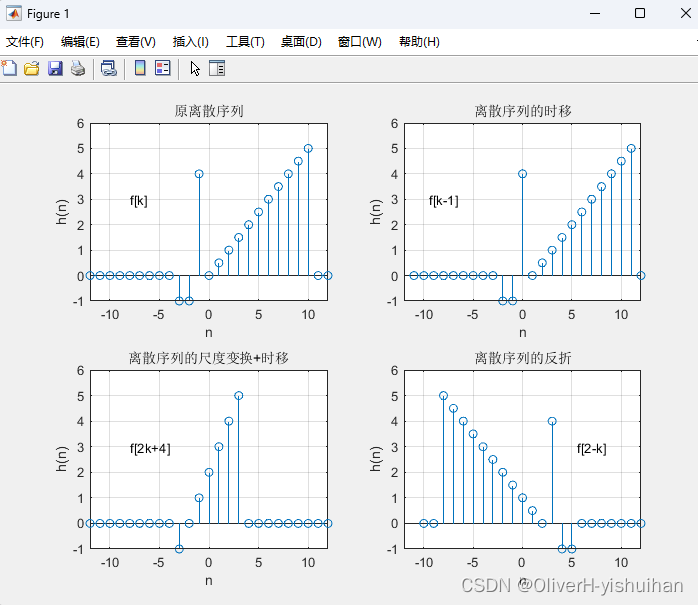
图像说明
- 原始离散序列 f[k]f[k]f[k]
- 离散序列 f[k−1]f[k - 1]f[k−1] 时移
- 离散序列 f[2k+4]f[2k + 4]f[2k+4] 尺度变换和时移
- 离散序列 f[2−k]f[2 - k]f[2−k] 反折效果
信号在 MATLAB 中的运算——信号的翻转与移位
Oliver-H 已于 2024-04-07 11:52:43 修改
序列的翻转和移位
序列翻转的表达式为:
y(n)=x(−n)y(n) = x(-n)y(n)=x(−n)
序列移位的表达式为:
y(n)=x(n−n0)y(n) = x(n - n_0)y(n)=x(n−n0)
在 MATLAB 中,翻转运算可通过函数 fliplr 实现。设序列 x(n)x(n)x(n) 用样值向量 xxx 和位置向量 nxnxnx 来描述,翻转后的序列 y(n)y(n)y(n) 用样值向量 yyy 和位置向量 nynyny 来描述。
y = fliplr(x);
ny = -fliplr(nx);
设序列 x(n)x(n)x(n) 用样值向量 xxx 和位置向量 nxnxnx 来描述,移位后的序列 y(n)y(n)y(n) 用样值向量 yyy 和位置向量 nynyny 来描述。
y = x; % 样值向量不变
ny = nx + n_0; % $n_0 > 0$,表示向右移动 $n_0$ 个位置;$n_0 < 0$,表示向左移动 $n_0$ 个位置
序列翻转示例
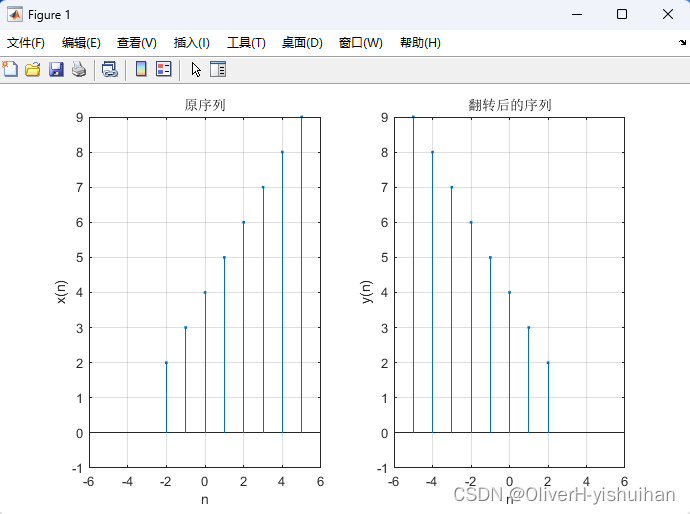
以下是序列翻转的 MATLAB 代码示例:
% E_5_11.m
% 序列翻转示例
clear, clc, clf;
nx = -2 : 5;
x = [2 3 4 5 6 7 8 9];
ny = -fliplr(nx);
y = fliplr(x);
subplot(121), stem(nx, x, '.');
axis([-6 6 -1 9]); title('原序列'); grid on;
xlabel('n'); ylabel('x(n)');
subplot(122), stem(ny, y, '.');
axis([-6 6 -1 9]); title('翻转后的序列'); grid on;
xlabel('n'); ylabel('y(n)');
set(gcf, 'color', 'w');
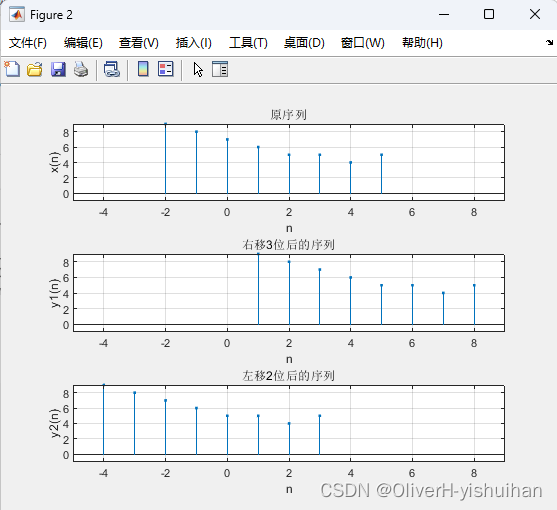
序列移位示例
以下是序列移位的 MATLAB 代码示例:
% E_5_12.m
% 序列移位示例
figure;
nx = -2 : 5; x = [9 8 7 6 5 5 4 5];
y = x; ny1 = nx + 3; ny2 = nx - 2;
subplot(311), stem(nx, x, '.');
axis([-5 9 -1 9]); grid;
xlabel('n'); ylabel('x(n)'); title('原序列');
subplot(312), stem(ny1, y, '.');
axis([-5 9 -1 9]); grid;
xlabel('n'); ylabel('y1(n)'); title('右移 3 位后的序列');
subplot(313), stem(ny2, y, '.');
axis([-5 9 -1 9]); grid;
xlabel('n'); ylabel('y2(n)'); title('左移 2 位后的序列');
via:
- Time Shifting, Time Scaling & Time Reversal of Signals | Electricalvoice
https://electricalvoice.com/time-shifting-time-scaling-time-reversal-of-signals/ - 信号的时间平移、反转、伸缩变换_信号时移-CSDN 博客
https://blog.csdn.net/liuyuanhuge/article/details/120476163 - 信号在 MATLAB 中的运算——信号的时移、反折和尺度变换_matlab 信号时移-CSDN 博客
https://blog.csdn.net/yishuihanq/article/details/130514804 - 信号在 MATLAB 中的运算——信号的翻转与移位_matlab 移位-CSDN 博客
https://blog.csdn.net/yishuihanq/article/details/130868736 - ……
