【LeetCode】454. 四数相加 II 【分组+哈希表】详解
【LeetCode】454. 四数相加 II 【分组+哈希表】详解
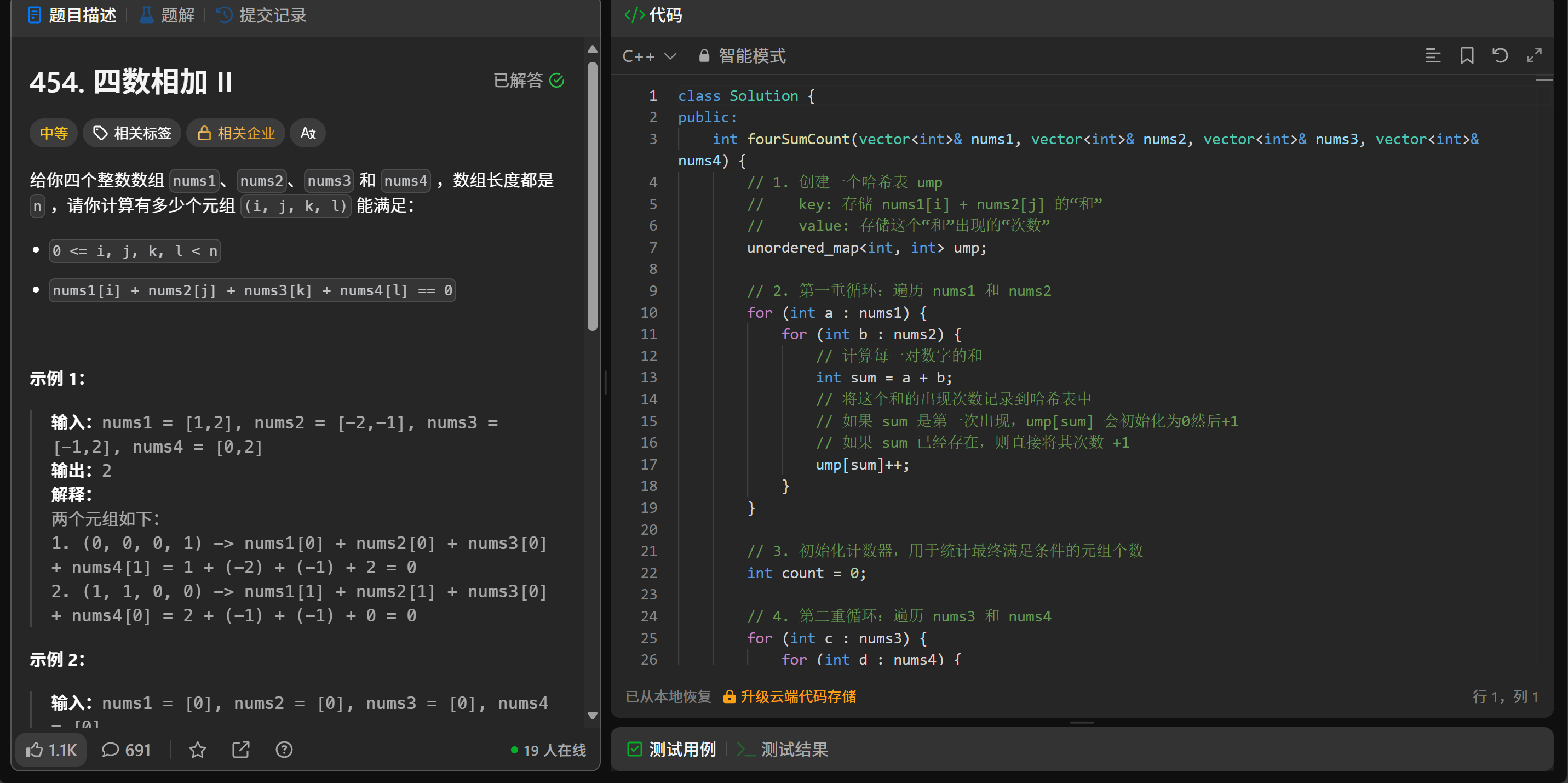
题目描述
题目链接:https://leetcode.com/problems/4sum-ii/
给你四个整数数组 nums1、nums2、nums3 和 nums4,数组长度都是 n。请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例 1:
输入: nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出: 2
解释:
两个元组如下:
- (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
- (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
示例 2:
输入: nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出: 1
解题思路
1. 暴力解法(不可行)
最直观的想法是使用四层循环遍历所有可能的组合,检查其和是否为0。这种方法的时间复杂度为 O(n⁴),当数组长度较大时(题目中 n 最大为 200),计算量会爆炸式增长,导致超时。
2. 优化思路:分组 + 哈希表
核心思想是 “空间换时间”,将四个数组分为两组,从而将问题规模降低。
- 分组: 将四个数组分成
(A, B)和(C, D)两组。 - 关键转换: 我们需要找的是
A[i] + B[j] + C[k] + D[l] = 0。
这可以转换为:A[i] + B[j] = - (C[k] + D[l])。
这样,我们就把一个“四数之和”问题,转化为了两个“两数之和”问题。
具体步骤:
-
遍历第一组 (A, B):
- 使用一个哈希表
map,key存储A[i] + B[j]的和,value存储这个和出现的次数。 - 通过一个两重循环,我们就能统计出所有
A+B的和及其出现的频率。
- 使用一个哈希表
-
遍历第二组 (C, D):
- 再使用一个两重循环,计算
C[k] + D[l]的和,记为sumCD。 - 在哈希表
map中查找是否存在key为-sumCD的记录。 - 如果存在,说明我们找到了
(A+B) = - (C+D)的组合。此时,哈希表中-sumCD对应的value(即出现的次数),就是当前(C[k], D[l])能与多少对(A[i], B[j])组成和为 0 的四元组。将这个value累加到结果中。
- 再使用一个两重循环,计算
复杂度分析:
- 时间复杂度: O(n²)。我们使用了两个独立的 O(n²) 循环。
- 空间复杂度: O(n²)。在最坏情况下,
A+B的和可能都不相同,哈希表需要存储 n² 个键值对。
代码实现(C++)
#include <vector>
#include <unordered_map>
using namespace std;class Solution {
public:int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {// 步骤1:创建哈希表,key存储a+b的和,value存储该和出现的次数unordered_map<int, int> sumMap;// 遍历nums1和nums2,计算所有a+b的可能for (int a : nums1) {for (int b : nums2) {int sumAB = a + b;sumMap[sumAB]++; // 对应和的次数加1}}// 步骤2:初始化计数器,统计最终结果int count = 0;// 遍历nums3和nums4,计算所有c+d的可能for (int c : nums3) {for (int d : nums4) {int sumCD = c + d;int target = -sumCD; // 我们需要在map中寻找的目标值是 -(c+d)// 检查map中是否存在这个目标值if (sumMap.find(target) != sumMap.end()) {// 如果存在,说明找到了符合条件的四元组// 个数为 sumMap[target],因为每一对(a,b)都可以和当前的(c,d)配对count += sumMap[target];}}}// 返回总的四元组个数return count;}
};
示例图解
我们以示例1来模拟一下算法过程:
输入: nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
第一步:构建哈希表 (遍历 nums1 和 nums2)
- 1 + (-2) = -1 ->
map[-1] = 1 - 1 + (-1) = 0 ->
map[0] = 1 - 2 + (-2) = 0 ->
map[0] = 2(0又出现了一次,所以值变为2) - 2 + (-1) = 1 ->
map[1] = 1
此时哈希表 map 为:{-1:1, 0:2, 1:1}
第二步:遍历查询 (遍历 nums3 和 nums4)
- c=-1, d=0 -> c+d = -1 -> 需要找 -(-1) = 1。
map中有 1,其值为 1。count += 1。 - c=-1, d=2 -> c+d = 1 -> 需要找 -1。
map中有 -1,其值为 1。count += 1。 - c=2, d=0 -> c+d = 2 -> 需要找 -2。
map中无 -2,跳过。 - c=2, d=2 -> c+d = 4 -> 需要找 -4。
map中无 -4,跳过。
最终结果: count = 1 + 1 = 2,与示例输出一致。
总结
本题的解法非常巧妙,通过 分组 和 利用哈希表记录中间结果,成功地将时间复杂度从 O(n⁴) 降低到了 O(n²),是“空间换时间”策略的经典应用。理解这种思想对解决此类“多数和”问题(如两数之和、三数之和)非常有帮助。
希望本篇题解对你有帮助!如果有任何疑问,欢迎在评论区留言讨论。
