【数据结构】汉诺塔问题

汉诺塔问题的核心解法是递归分治思想，通过将复杂问题拆解为规模更小的子问题，逐步解决。以下是该代码的具体思路解析：

1. 问题拆解：将 n 个圆盘的移动分解为 3 步

汉诺塔的目标是将 A 柱上的 n 个圆盘（从小到大堆叠，大圆盘在下）全部移动到 C 柱，B 柱作为辅助，且需遵守：①每次只能移动 1 个圆盘；②任何时候大盘不能放在小盘上。

对于 n 个圆盘，递归思路是：

• 第一步：先将 A 柱上的前 n-1 个圆盘借助 C 柱作为辅助，移动到 B 柱上（此时 A 柱只剩最大的第 n 个圆盘）；
• 第二步：直接将 A 柱上剩下的最大圆盘（第 n 个） 移动到 C 柱（此时最大圆盘已就位，无需再移动）；
• 第三步：再将 B 柱上的n-1 个圆盘借助 A 柱作为辅助，移动到 C 柱上（此时所有圆盘都转移到 C 柱，完成目标）。

2. 递归终止条件：最小子问题（n=1）

当 n=1 时（只有 1 个圆盘），无需拆解，直接将圆盘从 A 柱移动到 C 柱即可，这是递归的 “base case”，避免无限递归。

3. 代码对应逻辑

• hanoi(n, A, B, C)函数：递归核心，实现 “将 n 个圆盘从 A 柱经 B 柱辅助移到 C 柱”。
  • 若 n=1：直接调用move(A, 1, C)，完成单个圆盘的移动；
  • 若 n>1：按上述三步拆解，通过两次递归调用处理 n-1 个圆盘的移动，中间调用move处理最大圆盘。
• move(A, n, B)函数：辅助函数，打印移动过程（如a->c表示从 a 柱移动圆盘到 c 柱）。

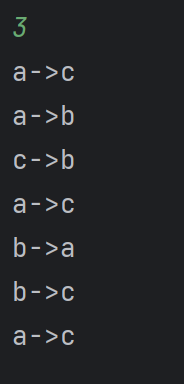
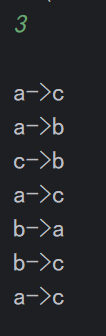
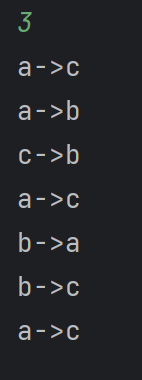
示例：n=3 时的执行流程

• 第一步：hanoi(2, A, C, B) → 将 A 上的 2 个圆盘移到 B（C 辅助）；
  • 其中又拆解为：hanoi(1, A, B, C)（A 的 1 个移到 C）→ move(A, 2, B)（A 的 2 移到 B）→ hanoi(1, C, A, B)（C 的 1 移到 B）；
• 第二步：move(A, 3, C) → 将 A 上的 3 号圆盘（最大）移到 C；
• 第三步：hanoi(2, B, A, C) → 将 B 上的 2 个圆盘移到 C（A 辅助）；
  • 其中又拆解为：hanoi(1, B, C, A)（B 的 1 移到 A）→ move(B, 2, C)（B 的 2 移到 C）→ hanoi(1, A, B, C)（A 的 1 移到 C）。

最终输出移动步骤，完成 3 个圆盘的转移。

核心思想

通过递归将 n 个圆盘的问题不断拆解为 n-1、n-2…… 直到 1 个圆盘的最小问题，利用辅助柱的切换，逐步实现目标。这种分治策略是解决汉诺塔问题的经典方法，时间复杂度为 O (2ⁿ)（需移动 2ⁿ-1 次）。

C++代码如下：

#include <iostream>
using namespace std;// 声明函数原型
void hanoi(int n, char A, char B, char C);
void move(char A, int n, char B);int main() {int n;cin >> n;               // 读取输入的圆盘数量hanoi(n, 'a', 'b', 'c');// 调用汉诺塔函数，初始柱子为a, b, creturn 0;
}// 移动函数：打印从A柱移动第n号圆盘到B柱的过程
void move(char A, int n, char B) {cout << A << "->" << B << endl;
}// 汉诺塔递归函数：将柱A上的n个圆盘按规则搬到C上，B做辅助柱
void hanoi(int n, char A, char B, char C) {if (n == 1) {move(A, 1, C);  // 将编号为1的圆盘从A柱移到C柱} else {hanoi(n-1, A, C, B);  // 将A上编号为1至n-1的圆盘移到B, C做辅助柱move(A, n, C);        // 将编号为n的圆盘从A移到Chanoi(n-1, B, A, C);  // 将B上编号为1至n-1的圆盘移到C, A做辅助柱}
}

Python代码如下：

def hanoi(n, A, B, C):"""将柱A上的n个圆盘按规则搬到C上，B做辅助柱"""if n == 1:move(A, 1, C)  # 将编号为1的圆盘从A柱移到C柱else:hanoi(n-1, A, C, B)  # 将A上编号为1至n-1的圆盘移到B, C做辅助柱move(A, n, C)  # 将编号为n的圆盘从A移到Chanoi(n-1, B, A, C)  # 将B上编号为1至n-1的圆盘移到C, A做辅助柱def move(A, n, B):"""打印从A柱移动第n号圆盘到B柱的过程"""print(f"{A}->{B}")if __name__ == "__main__":n = int(input())hanoi(n, 'a', 'b', 'c')

Java代码如下：

import java.util.Scanner;public class Hanoi {// 移动方法：打印从A柱移动第n号圆盘到B柱的过程public static void move(char A, int n, char B) {System.out.println(A + "->" + B);}// 汉诺塔递归方法：将柱A上的n个圆盘按规则搬到C上，B做辅助柱public static void hanoi(int n, char A, char B, char C) {if (n == 1) {move(A, 1, C);  // 将编号为1的圆盘从A柱移到C柱} else {hanoi(n - 1, A, C, B);  // 将A上编号为1至n-1的圆盘移到B, C做辅助柱move(A, n, C);          // 将编号为n的圆盘从A移到Chanoi(n - 1, B, A, C);  // 将B上编号为1至n-1的圆盘移到C, A做辅助柱}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();  // 读取输入的圆盘数量hanoi(n, 'a', 'b', 'c');   // 调用汉诺塔方法，初始柱子为a, b, cscanner.close();}
}