磁共振成像原理（理论）20：K空间采样 (Sampling of k-Space) - 采样定理

首先，我们回顾一些关于带限信号的基本定义，这是理解采样定理的基础。

定义1： 一个时间信号$g(t)$，如果对于 $|t|>T$ 有 $g(t)=0$，其中 $T$ 是一个有限数，则该时间信号$g(t)$ 被称为是时间有限的。

定义2：一个时间信号$g(t)$ ，如果其频率谱 {Fg}(f)\{\mathcal{F}g\}(f){Fg}(f) 对于 $|f|>f_{\text{max}}$ 为零，其中 $f_{\text{max}}$ 是信号的频率带宽，则该时间信号$g(t)$被称为是（频率）带限的。

定义3： 一个空间信号$g(x)$ ，如果对于 $|x|>W$ 有 $g(x)=0$，则该空间信号$g(x)$被称为是空间有限的

定义4： 一个空间信号 $g(x)$ ，如果其空间频率谱 {Fg}(k)\{\mathcal{F}g\}(k){Fg}(k) 对于 $|k|>k_{\text{max}}$ 为零，其中 $k_{\text{max}}$ 是信号的空间频率带宽，则该空间信号 $g(x)$ 被称为是(空间频率)带限的

均匀采样以及信号重建

香农采样定理指出，一个带限函数可以从其以不超过信号带宽两倍的倒数为间隔进行的均匀采样值中完美地重建。

更具体地说，设 $g(t)$ 的带宽限制为 $f_{\text{max}}$。采样定理要求采样间隔 $\Delta t$ 满足：
$$\Delta t\le \frac{1}{2f_{\text{max}}}or{f}_s=\frac{1}{\Delta t}\ge 2f_{\text{max}}\text{\hspace{1em}(5.114)}$$

这被称为奈奎斯特采样准则。奈奎斯特准则所允许的最大采样间隔是 $\Delta t=1/(2f_{\text{max}})$，这被称为奈奎斯特间隔。相应地，$f_s=2f_{\text{max}}$ 被称为奈奎斯特频率，这是精确恢复 $g(t)$ 所需的最小采样率。

其中采样过程可以建模为原始信号与冲激串的乘积：
$$g_s(t)=g(t)\cdot \sum _{n=-\infty }^{\infty }\delta (t-n\Delta t)=\sum _{n=-\infty }^{\infty }g(n\Delta t)\delta (t-n\Delta t)$$
其中 $g_s(t)$ 是采样后的信号，其傅里叶变换为：
Gs(f)=F{gs(t)}=fs∑k=−∞∞G(f−kfs) G_s(f) = \mathcal{F}\{g_s(t)\} = f_s \sum_{k=-\infty}^{\infty} G(f - kf_s) Gs​(f)=F{gs​(t)}=fs​k=−∞∑∞​G(f−kfs​)

由于 $g(t)$ 是带限的，且满足 $f_s\ge 2f_{\text{max}}$，$G_s(f)$ 中的频谱周期延拓不会发生混叠。

为了从采样信号$g_s(t)$中完美重建原始信号，需要使用理想低通滤波器，将上述延拓的频谱滤除：
$$H(f)=\{\begin{array}{ll}\Delta t=\frac{1}{f_s},& |f|\le f_s/2\\ 0,& |f|>f_s/2\end{array}$$

该滤波器在通带内的增益为 $\Delta t$，截止频率为 $f_s/2$。理想低通滤波器 $H(f)$ 的逆傅里叶变换为 $sinc$ 函数，其中 $\text{sinc}(x)=\frac{\sin (\pi x)}{\pi x}$：
h(t)=F−1{H(f)}=sin(πfst)πt=fs⋅sinc(fst) h(t) = \mathcal{F}^{-1}\{H(f)\} = \frac{\text{sin}(\pi f_s t)}{\pi t} = f_s \cdot \text{sinc}(f_s t) h(t)=F−1{H(f)}=πtsin(πfs​t)​=fs​⋅sinc(fs​t)

在频域中将$G_s(f)$乘以理想低通滤波器$H(f)$，对应的就是在时域中，将$g_s(t)$和$h(t)$进行卷积得到重建信号 $g_r(t)$ ：
$$\begin{array}{rl}{g}_r(t)& =g_s(t)\ast h(t)\\ & =\left[\sum _{n=-\infty }^{\infty }g(n\Delta t)\delta (t-n\Delta t)\right]\ast \text{sinc}(\pi f_{s}t)\\ & =\sum _{n=-\infty }^{\infty }g(n\Delta t)\cdot \text{sinc}[\pi f_s(t-n\Delta t)]\end{array}$$

因此，我们得到著名的香农插值公式：
$$g(t)=\sum _{n=-\infty }^{\infty }g(n\Delta t)\mathrm{sinc}[\pi f_s(t-n\Delta t)]\text{\hspace{1em}(5.115)}$$

这个关系在下图中进行了说明：每一个采样点处放置一个$sinc$函数，幅值为$g_s(t)$，即可恢复原始信号。

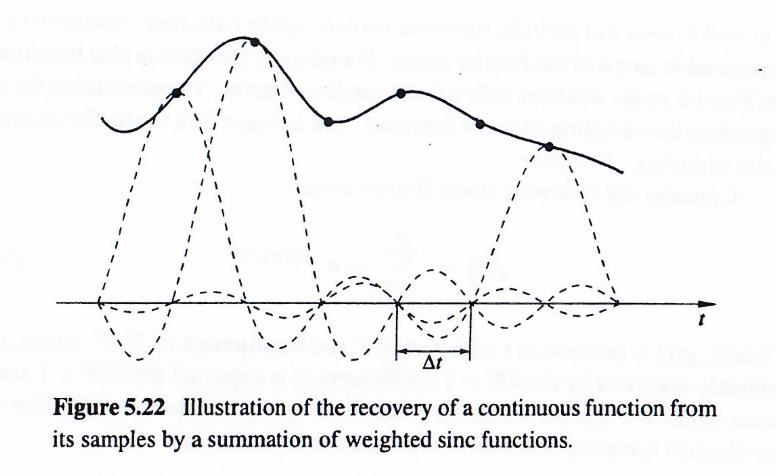
同样容易证明，方程 (5.115) 可以根据信号带宽表示为：
$$g(t)=\frac{2f_{\text{max}}}{f_s}\sum _{n=-\infty }^{\infty }g(n\Delta t)\mathrm{sinc}[2\pi f_{\text{max}}(t-n\Delta t)]\text{\hspace{1em}(5.116)}$$
注意：在实际应用中，由于只能进行有限项求和，重建会存在误差。此外，理想的 sinc 函数是无限长的，需要截断处理，这也会引入吉布斯现象等误差。这些都会在后面进一步介绍。

交错采样

交错采样是非均匀采样的一个特例，它在回波平面成像中有着重要的应用。如下图所示。

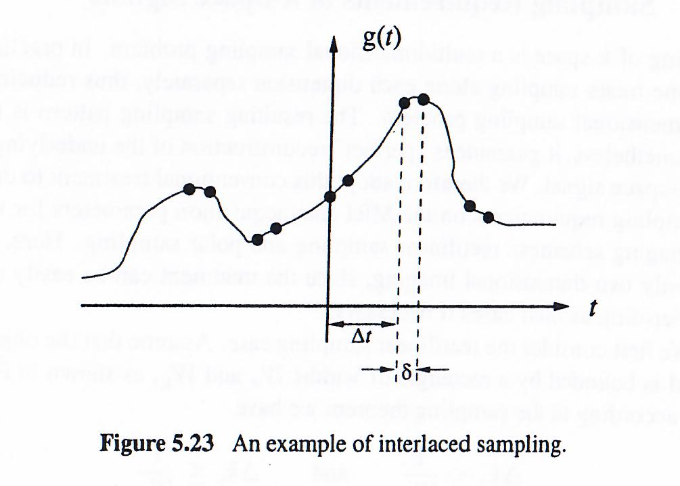
如果 $\Delta t\le 1/f_{\text{max}}$，交错采样在平均意义上满足奈奎斯特准则。$g(t)$ 可以使用以下插值公式从这组非均匀采样值中恢复：
$$g(t)=\sum _{n=-\infty }^{\infty }\left[g(n\Delta t)h(t-n\Delta t)+g(n\Delta t+\delta )h(-t+n\Delta t+\delta )\right]\text{\hspace{1em}(5.117)}$$

其中插值核函数 $h(t)$ 由下式给出：
$$h(t)=\frac{\cos (2\pi f_{\text{max}}t-\pi \delta f_{\text{max}})-\cos (\pi \delta f_{\text{max}})}{2\pi f_{\text{max}}t\sin (\pi \delta f_{\text{max}})}\text{\hspace{1em}(5.118)}$$

公式5.117和5.118的完整推导过程见《Introduction to Shannon Sampling and Interpolation Theory》。

带限周期函数的采样

众所周知，周期函数（满足狄利克雷条件）可以用傅里叶级数表示。如果一个周期函数同时也是带限的，那么其傅里叶级数将只有有限项。我们在此总结关于这些函数采样的结果，因为它对于描述$k$空间的极坐标采样非常有用。

考虑以下有限项傅里叶级数：
$$g(t)=\sum _{n=-N}^N{c}_n{e}^{-i2\pi nt/T}\text{\hspace{1em}(5.119)}$$

显然，$g(t)$ 是周期为$T$的时间$t$的函数，并且带宽限制为 $N/T$。由于 $g(t)$ 由 $2N+1$ 个系数唯一确定，因此预计在一个周期内采集 $2N+1$ 个样本就足以唯一地重建 $g(t)$。所以，这种情况下的奈奎斯特采样准则可以表述为：
$$\Delta t\le \frac{T}{2N+1}\text{\hspace{1em}(5.120)}$$

假设在区间 $\Delta t=T/N_s$ 内从 $g(t)$ 中采集了 $N_s\ge 2N+1$ 个样本。研究表明，$g(t)$ 可以使用以下插值公式从这组样本中重建：
$$g(t)=\sum _{n=0}^{N_s-1}g(n\Delta t)\frac{\sin \left[\frac{\pi }{T}(2N+1)(t-n\Delta t)\right]}{N_s\sin \left[\frac{\pi }{T}(t-n\Delta t)\right]}\text{\hspace{1em}(5.121)}$$

方程 (5.121) 的详细推导可以在 《Advanced Topics in Shannon Sampling And Interpolation Theory》中找到。