偏振光阴影投影的三元光学逻辑处理器

摘要：

使用有符号数字的三态逻辑可用于无进位和无借位的数学运算。本文探讨了基于三态的基本逻辑系统及其基于阴影投射技术的实现。

1. 引言

并行处理可以通过光学技术实现，用于执行计算和逻辑运算。然而，并行执行算术运算的主要限制在于，进位或借位不易处理。由于数据或数字通​​常以二进制形式存在，因此，用带符号数字 { 1, 0,i } 进行符号替换的技术显得尤为重要 [1-5]。Datta 等人 [6] 提出了一种改进的三进制数 (MTN) 系统，该系统可以并行执行任何二进制数，而无需在将二进制数字转换为 MTN 系统时进行进位和借位运算。本文提出了一种 MTN 系统的光学实现。本方法是无透镜阴影投射技术的扩展，该技术最初由 Tanida 和 Ichioka [7-9] 提出。三种空间编码用于对三种输入状态进行编码，而在解码平面中，三个状态分别由无光和具有两种正交偏振态的光来标识。

2. 使用 MTN 系统的逻辑门

在 MTN 系统中，与二进制逻辑中的两种状态不同，需要生成三种不同的状态来表示 1、0 和 i。逻辑公式基于 1、0 和 i 的定义，即1 为真；0 为空/矛盾；i 为假。这意味着，如果信息为真，则用 1 表示；如果信息为假，则用 i 表示；0 表示无信息状态或信息

部分真部分假的状态。零的定义是可行的，因为我们知道，我们不能只从部分真部分假的状态中获得信息。因此，从信息的角度来看，这种状态等同于零状态，即没有信息的状态。

在讨论逻辑门的实际实现之前，我们首先定义三进制系统中的逻辑门。

(a) 与门：A^B。与门运算分别在两个信息为真或为假的情况下，输出带符号的1或i。在所有其他情况下，输出为0。

(b) 或门：A vB。或门意味着两个输入中至少有一个信息必须为真或为假，但当一个输入为真而另一个为假时，情况无法确定，因此为零状态。

(c) 补码：A'。真的补码为假，反之亦然，但零状态是矛盾状态或为零。矛盾状态的补码也是矛盾的，也用0 表示。“与”、“或”和“补”的真值表如表 1 所示。通过对这些门进行排列组合，我们可以定义不同的门，其中一些列于表 2 中。

表1

表二

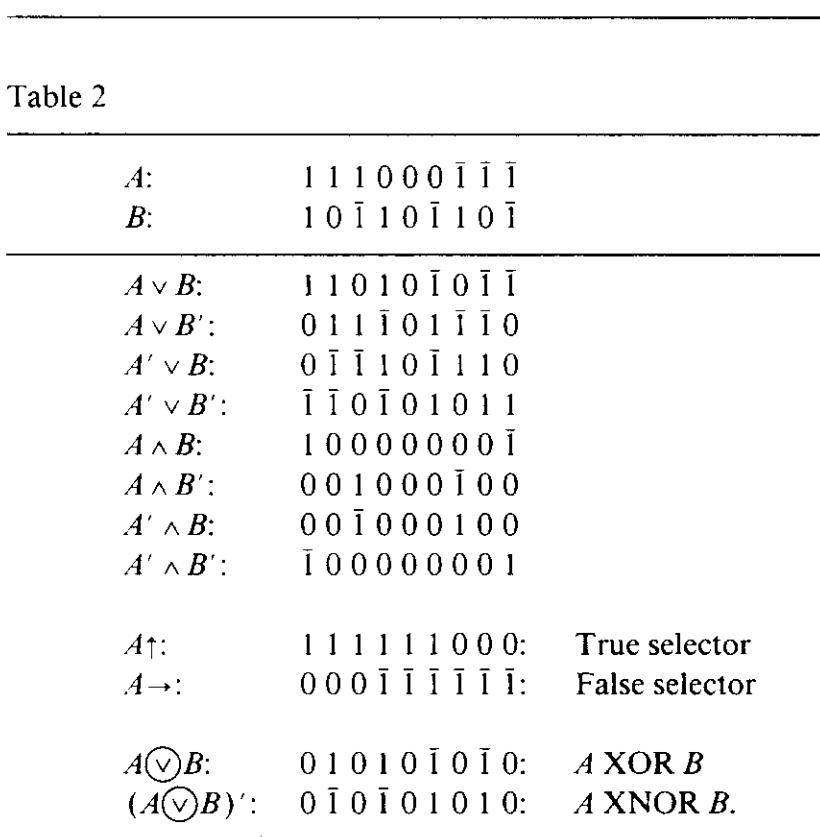
3. 逻辑门的光学实现

为了实现逻辑门，我们为每个输入 A 和 B 设置了三种像素 [8]。这些输入及其可能的组合如图 1 所示。每个像素由两部分组成——不透明和透明。每个像素的三分之一部分是透明的，其余部分是不透明的。因此，当这两种像素组合在一起时，只有九分之一的像素保持透明，如图 1 所示。

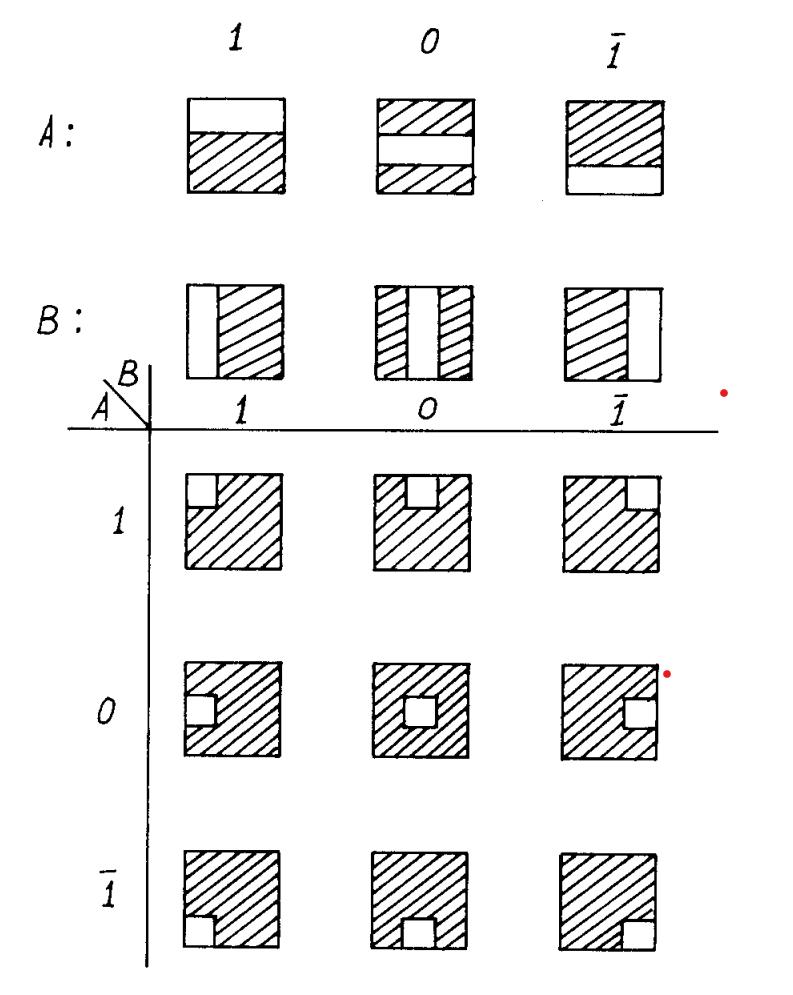
图 1. 输入 A 和 B 针对三种状态（i、0 和 1）及其组合的代码模式。

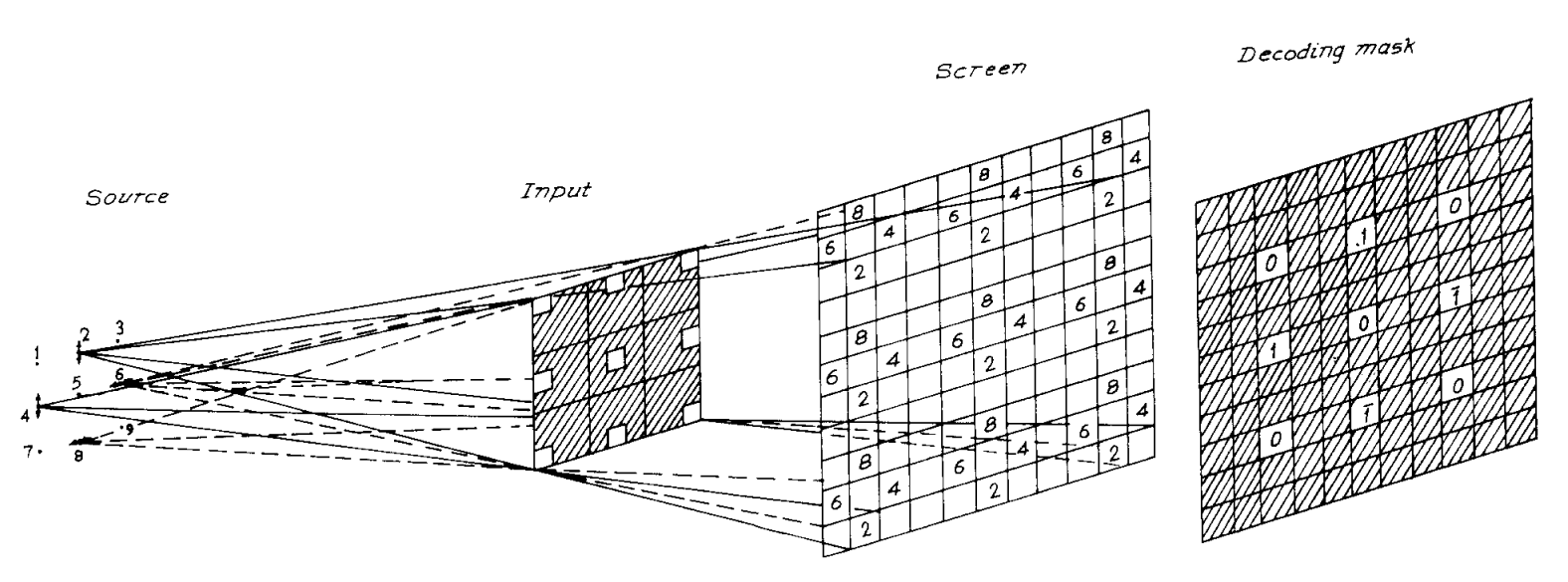
图2. 用于实现光学三进制逻辑门的阴影投射系统示意图。图中显示了XOR的实现。

图 2 是逻辑门的无透镜阴影投射实现示意图。九个LED 按图 2 所示排列，并配有一个偏振装置，该装置可用于将每个 LED 偏振到两种偏振状态之一[即水平偏振 (±) 和垂直偏振 ($)]。通过组合开启的LED及其偏振状态，可以实现不同的逻辑运算。LED光的偏振状态可以通过放置在每个LED前面的电信号表面稳定铁电液晶[10]来选择。

表3列出了并行执行各种逻辑运算时LED的状态。

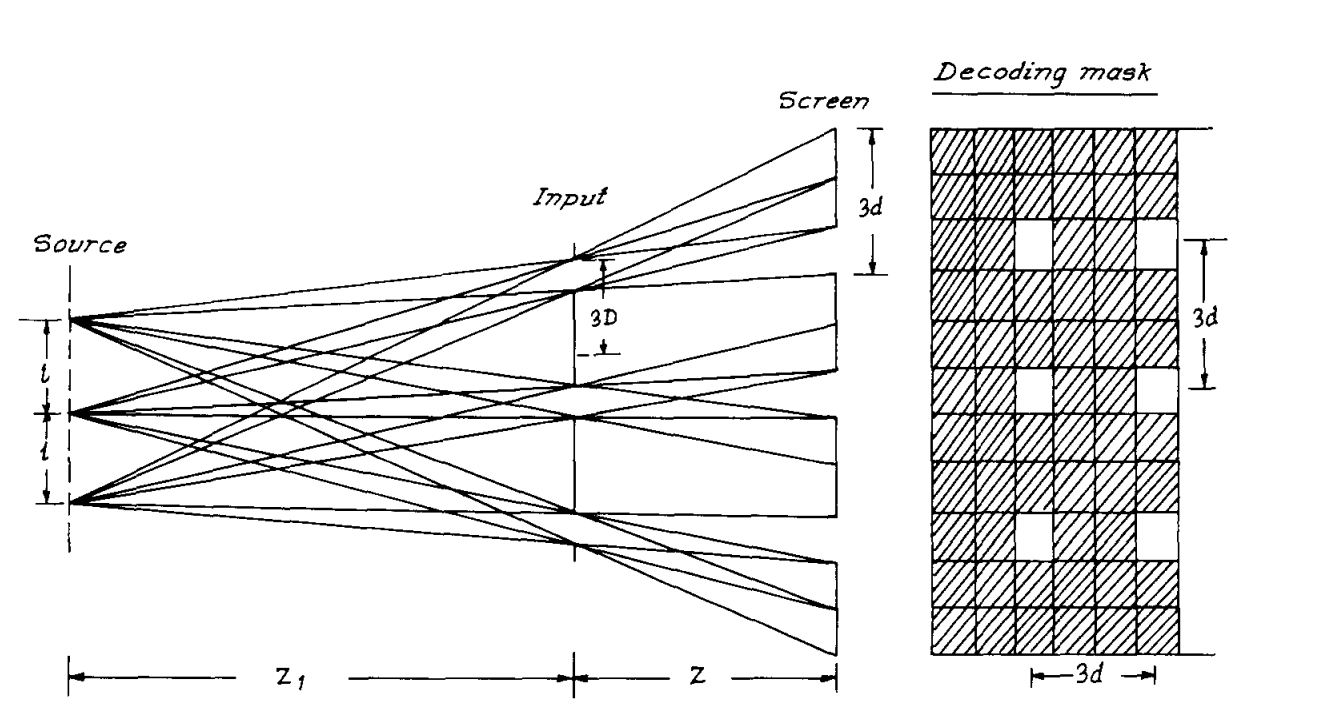
图3显示了该系统的几何结构。LED之间的不同间距以及单元和解码掩模的尺寸，可以通过使用与Tanida [7]相同的关系式获得。条件如下：

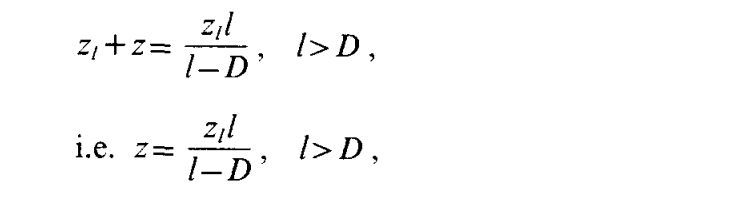
其中 3D = 输入像素的大小；3d = 投影图像图像平面中输入像素的大小；f = 源平面中任意两个光源之间的间距，zz = 光源与输入平面之间的距离；z = 输入平面与屏幕之间的距离。

4. 结论

在本篇通讯中，我们提出了三态逻辑门的真值表以及一种光学方法来实现它。虽然

这里的编码和译码与二进制相比更加复杂，但是，由于采用有符号数实现，数学运算可以实无进位和无借位。此外，这种三态逻辑也可用于图像处理。这些可能性正在未来的研究中。