《基于 ERT 的稀疏电极机器人皮肤技术》ICRA2020论文解析

目录
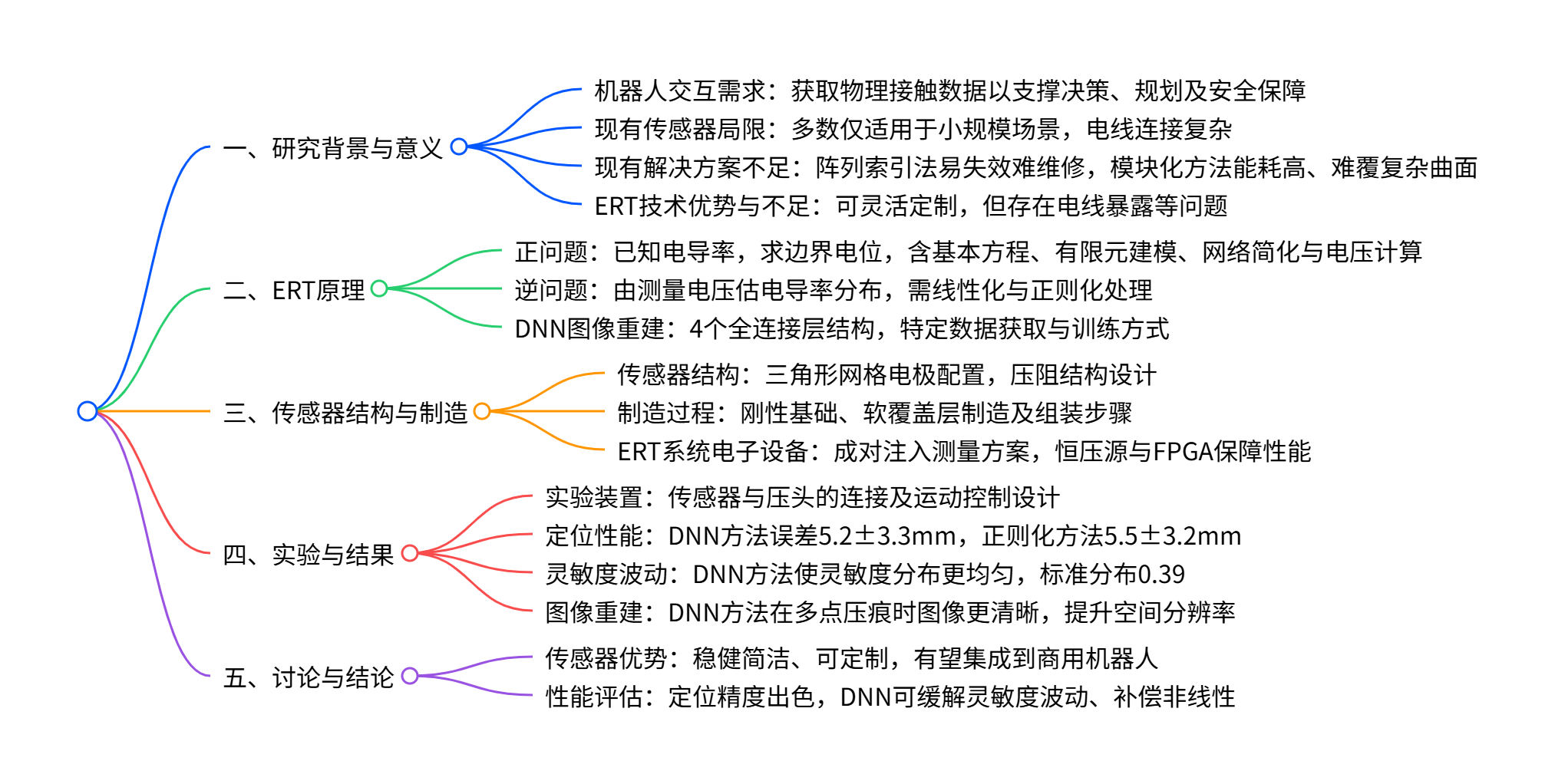
一、研究背景与意义
二、电阻抗断层成像(ERT)原理
(一)正问题
(二)逆问题
(三)基于深度神经网络(DNN)的图像重建
三、传感器结构与制造
(一)传感器结构
(二)制造过程
(三)ERT 系统电子设备
四、实验与结果
(一)压痕实验装置
(二)定位性能
(三)灵敏度波动
(四)图像重建结果
五、讨论与结论
一、研究背景与意义
在非结构化环境中,机器人与人类交互时,需获取周围环境信息以支撑决策制定、运动规划及保障人类安全。视听数据虽能助力机器人识别外部环境,却难以获取物理接触相关数据。而物理接触数据与视觉数据结合,可让机器人完成接触密集型任务,因此开发全身型机器人触觉皮肤十分必要。
当前多数触觉传感器仅适用于指尖传感器等小规模场景,难以扩展到大规模应用,核心障碍在于随着感应点数量增加,电线连接会变得极为复杂。为解决这一问题,研究人员提出了多种方案,但均存在不足:
- 阵列索引法:借助正交排列电极,通过电极组合获取感应点数据,虽能减少电极数量,可一旦某一电极失效,与之相关的所有感应点都会无法使用,且传感器维修难度大。
- 模块化方法:各传感器模块独立测量电压、电容等物理量,通过串行通信传输数据,仅需少量通道。不过每个模块都配备独立微控制单元(MCU),模块数量增多会导致能耗上升,且基于柔性 PCB 的模块化传感器难以覆盖复杂曲面。
相比之下,电阻抗断层成像(ERT)技术凭借独特工作原理,为实现大型弯曲柔性触觉传感器提供了新思路。ERT 通过少量边界电极就能估算内部感应区域的电导率分布,感应点与电极无直接连接,可根据应用需求灵活定制传感器形状和电极配置。但此前基于 ERT 的触觉传感器存在电线暴露、附着时产生建模误差以及难以覆盖圆柱面等问题,本文正是针对这些问题展开研究。
二、电阻抗断层成像(ERT)原理
ERT 原本是用于探测地下结构的地球物理技术,与用于医学成像和工业应用的电阻抗断层成像(EIT)关系密切。其核心优势是基于已知物理模型,利用边界电压就能通过数学方法重建感应区域的电导率分布,主要包含正问题和逆问题两部分,还可借助开源 MATLAB 库 EIDORS 实现数值计算,该库涵盖网格生成、驱动模式、正问题求解、图像重建等功能。
(一)正问题
正问题是在已知电导率等条件下,模拟传感器的电学行为,求解边界电位。
- 基本方程:对于导电区域 Ω 及其边界∂Ω,在直流且无内部电流源的假设下,麦克斯韦方程组给出边界电位 φ 与电导率分布 σ 的关系为\(\nabla \cdot(\sigma \nabla \phi)=0\)(在 Ω 内)。若已知电导率,结合边界条件\(j=\sigma \nabla \phi \cdot n\)(在∂Ω 上,其中 j 是电流密度,n 是∂Ω 的外法向单位向量),可求解边界电位,这属于拉普拉斯椭圆型偏微分方程的狄利克雷 - 诺伊曼边值问题。
- 有限元法建模:为求解上述方程,先构建有限元法(FEM)正向模型,该模型由节点及相邻节点连接而成,可等效为传感器的无源电阻网络。导电区域的电学行为可用传递阻抗矩阵\(R(\sigma) \in \mathbb{R}^{N ×N}\)描述,即\(v(\cdot ;\sigma ,i)=R(\sigma ) i\),其中\(i \in \mathbb{R}^{N}\)是通过有限元的电流,\(v \in \mathbb{R}^{N}\)是其两端的电位。
- 网络简化与电压变化计算:由于电流仅能通过电极对应的节点注入,可忽略其他节点简化网络,得到\(\hat{v}(\cdot ; \sigma, p)=S(\sigma) p\),其中\(p \in \mathbb{R}^{L}\)是注入电极的电流向量,\(\hat{v} \in \mathbb{R}^{L}\)是电极上产生的电压,\(S(\sigma) \in \mathbb{R}^{L ×L}\)是仅考虑电极对应 L 个节点的简化网络传递阻抗矩阵。对于电导率变化\(\Delta \sigma\),测量电压变化\(\Delta e\)可表示为\(m^{T}(S(\sigma+\Delta \sigma)-S(\sigma)) p\)(m 为测量模式向量)。将注入和测量向量扩展到矩阵形式,可得\(\Delta E=M^{T}(\Delta S) P\),进一步向量化后有\(\Delta E_{v e c}=\left(P^{T} \otimes M^{T}\right) \Delta S_{v e c}=G \Delta S_{v e c}=J \Delta \sigma\),其中 J 为雅可比矩阵,反映电导率变化\(\Delta \sigma\)与\(\Delta E_{v e c}\)的关系。
(二)逆问题
逆问题是根据测量到的电压估算电导率分布,该问题具有不适定性和非线性,需通过线性化和正则化求解。
- 线性化近似:将电导率 σ 与测量电位 E 的非线性关系近似为线性方程\(\Delta E_{v e c}=J\Delta \sigma+w\)(w 为测量噪声),然后通过计算雅可比矩阵 J 的伪逆求解线性化逆问题。但对于精细网格,J 的秩小于网格单元数量,计算伪逆难度大。
- 正则化处理:引入基于先验信息(如空间高通滤波器或 NOSER)的正则化矩阵\(\Gamma \in \mathbb{R}^{M ×M}\),通过最小化代价函数\(\lambda(\Delta \sigma)=\| \delta E-J \Delta \sigma\| _{2}^{2}+\| \alpha \Gamma \Delta \sigma\| _{2}^{2}\)(α 为调节正则化程度的超参数)来求解,最终得到\(\Delta \tilde{\sigma}=\left(J^{T} J+\alpha^{2} \Gamma^{T} \Gamma\right)^{-1} J^{T} \delta E=Q \delta E\)(Q 为正则化线性重建矩阵),实现重建图像的解析稳定。
(三)基于深度神经网络(DNN)的图像重建
尽管通过近似逆问题能获得稳定输出图像,但受正则化和线性化影响,图像仍存在模糊和失真问题。迭代重建方法虽能提高精度,却因计算成本高、采样频率难以满足机器人皮肤应用需求而不实用。
DNN 在处理 ERT 逆问题非线性方面表现出色,且计算速度快。本文采用的 DNN 结构如图 2 所示
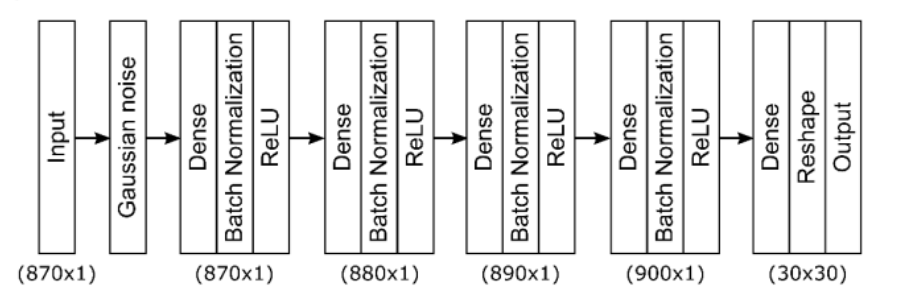
包含 4 个全连接层,各隐藏层神经元数量从前往后依次为 870、880、890 和 900。各隐藏层输入变量经批量归一化处理,激活函数采用 ReLU 函数。
- 训练数据获取:通过求解 3D ERT 模型的正问题获取训练数据,在传感器多个位置施加高斯形电导率扰动,将自动生成的网格上的电导率图像映射到 30×30 矩形网格,以扰动后的电导率图像作为输出变量,根据给定电导率扰动和电极模式(采用相邻模式,电压向量长度为 870)获取模拟电压,经归一化后作为输入变量。训练数据集包含约 110 万个样本,测试数据集含 4 万个样本,且测试数据集根据训练数据集的均值和标准差进行归一化。
- 模型训练:在配备 12GB 显存的 NVIDIA GeForce GTX Titan 显卡上进行训练,代码基于 Keras 编写,采用均方误差作为损失函数,Adam 优化器以实现快速稳健的训练。训练过程中,向输入张量添加具有实测标准差的高斯噪声以起到正则化作用,避免超参数的启发式选择,批处理大小设为 360。每个 epoch 都会在测试数据集上进行验证,最终验证损失收敛到 6.42e-4,训练损失收敛到 6.17e-4。
三、传感器结构与制造
(一)传感器结构
为实现性能优良的触觉传感器,需合理设计传感器结构,兼顾空间分辨率、灵敏度等性能,其结构如图 3 所示。
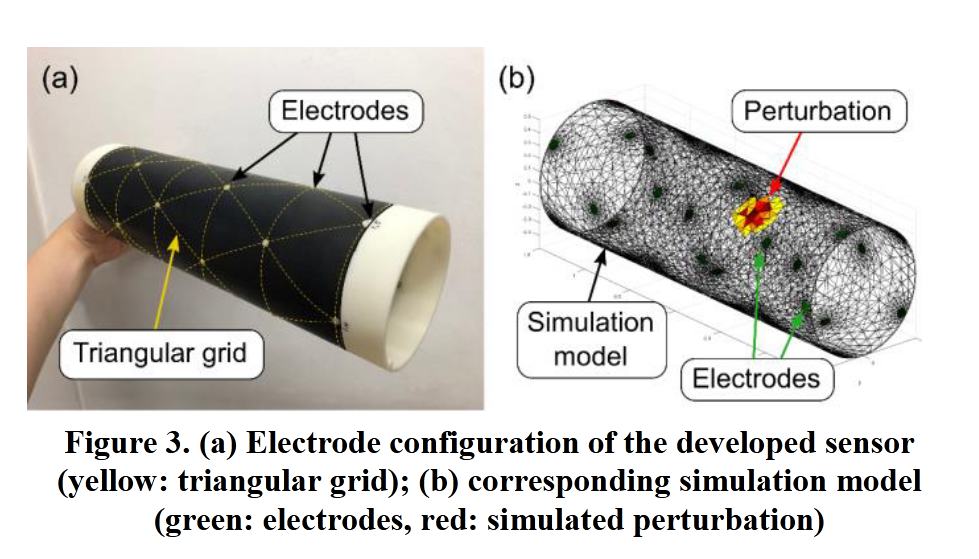
- 电极配置:ERT-based 触觉传感器虽能用少量电极估算外部刺激,但电极位置会影响传感器性能。若感应区域远离电极,电流密度低,会导致灵敏度和空间分辨率下降。因此,本文将电极均匀分布在整个感应区域,在圆柱面上形成三角形网格(图 3 中黄色虚线所示),电极位于网格节点处。传感器对应的网格模型中,圆柱长度 300mm、直径 100mm,共 30 个电极,分为 6 组,每组 5 个,每组电极位于圆柱同一横截面,呈等角度分布,组间间距 60mm。电线连接在电极下方,电极通过电线与 ERT 多路复用板相连。
- 压阻结构:感应区域需同时具备导电性和压阻性。借鉴 Tawil 等人的研究,采用基于接触的传导机制,将高导电织物贴片附着并按压在基础导电区域,产生接触电阻,电流通过织物贴片时面电阻局部降低。本文在机器人皮肤刚性体上形成导电表面,并覆盖高导电层,以实现压阻特性。
(二)制造过程
传感器由两部分组成:带有多个嵌入式电极的导电涂层刚性体和带有高导电织物贴片的软覆盖层,制造流程如图 4 所示。
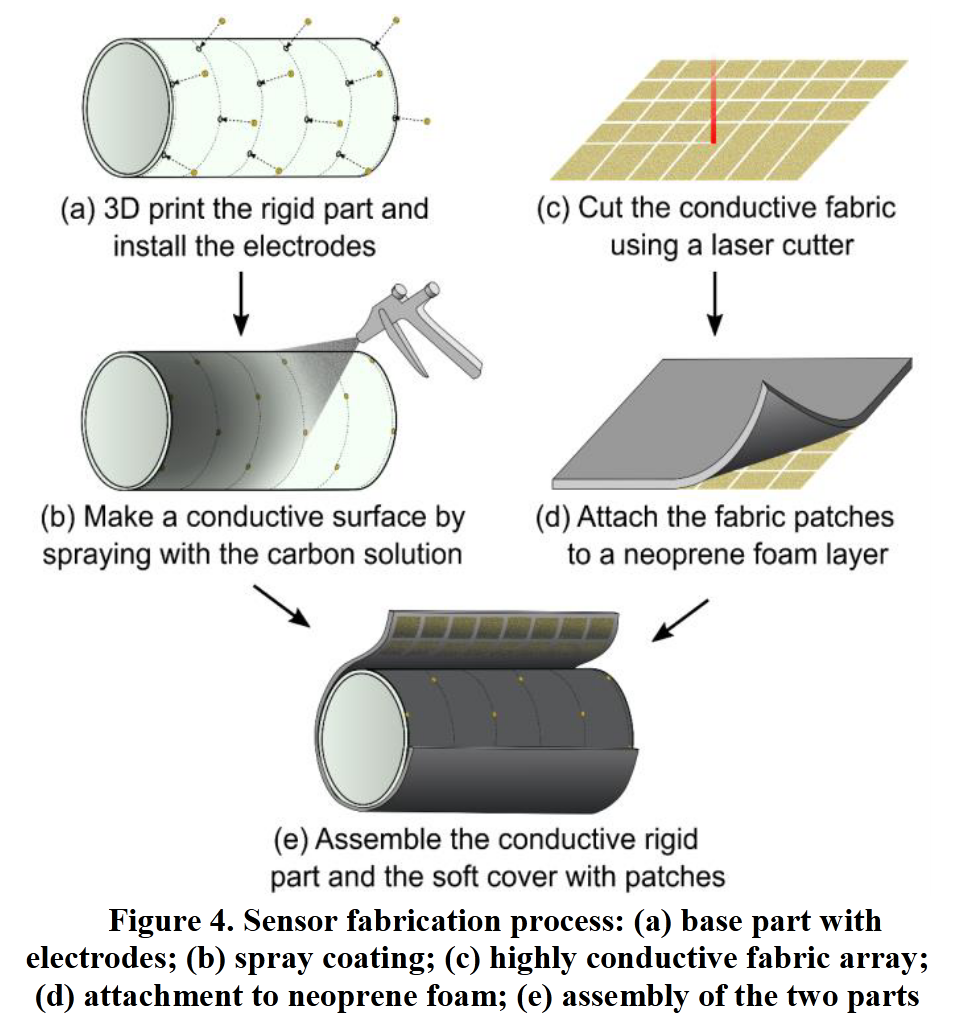
- 刚性基础部分制造:
- 采用 3D 打印机(美国 Stratasys 公司的 Dimension Elite)打印刚性基础部分,并用环氧树脂(美国 Smooth-On 公司的 XTC-3D)处理,再进行打磨以获得良好的表面状态。
- 在刚性体上安装电极,用电线将电极与连接器连接。
- 多次喷涂碳纳米管(CNT)分散溶液(韩国韩华公司的 HANOS),直至达到合适的面电阻,形成导电表面。
- 在电极上涂抹银浆(日本 CANS 公司的 ELCOAT P-100),确保涂层表面与电极之间形成稳定的电连接,待银浆充分干燥后,刚性基础部分制造完成。
- 软覆盖层制造:
- 采用可拉伸聚氨酯(PU)薄膜(德国 Vlieseline 公司的 Stretchfix)和高导电织物(德国 Statex 公司的 Med-tex P130)制作软覆盖层。通过熨烫将 PU 薄膜附着在织物上,然后用激光切割机将织物切割成阵列贴片。
- 将氯丁橡胶泡沫放置在阵列贴片上,并用胶水固定。
- 组装:将软覆盖层覆盖在传感器刚性部分上,利用 CNT 涂层与高导电织物贴片之间的接触电阻,使制成的传感器具备压阻特性。
(三)ERT 系统电子设备
ERT-based 传感器需在电极上进行电流注入和测量,系统原理如图 5 所示。本文采用成对注入和测量方案,电极与多路复用器(美国 ADI 公司的 ADG1206)连接,多路复用器由数据采集卡(DAQ,美国国家仪器公司的 myRIO-1900)控制。多路复用器还分别与电流源和电压测量通道连接,以实现电极的电流注入和电压测量。
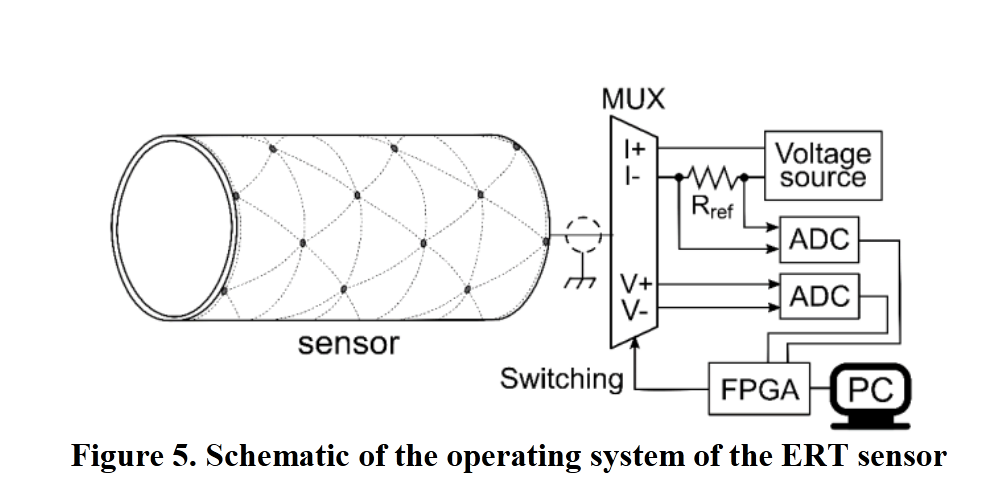
- 系统未采用恒流源,而是使用恒压源和串联的参考电阻进行补偿。
- DAQ 配备 FPGA 芯片,开关和测量频率可达 120kHz,得益于高采样率,传感器帧率能达到 120Hz。
四、实验与结果
(一)压痕实验装置
实验装置如图 6 所示

传感器固定在轴上并与步进电机连接。压头由音圈(VC)电机、测力传感器和球形尖端组成,安装在直线运动导轨上,通过同步带与另一台步进电机连接,可沿直线导轨移动。实验中,在 30×30 矩形网格的节点处对传感器进行 900 次压痕测试。当压头移动到合适位置后,对传感器进行压痕操作,同时记录传感器输出、位置和力值,用于评估传感器的定位精度、空间灵敏度分布和成像清晰度等性能。
(二)定位性能
分别采用正则化方法(线性)和基于 DNN 的方法,将实验数据转换为 30×30 的电导率图像,根据公式\(\left(x_{m}, y_{m}\right)=\left(\frac{\sum m_{i} x_{i}}{\sum m_{i}}, \frac{\sum m_{i} y_{i}}{\sum m_{i}}\right)\)(i=1,...,900,\(m_i\)为重建图像像素值,\(x_i,y_i\)为像素坐标)计算重建图像的质心\((x_m,y_m)\),并与压痕位置进行比较。
- 基于 DNN 方法的定位误差为 5.2±3.3mm,正则化方法的定位误差为 5.5±3.2mm,相比之前的研究,传感器定位性能显著提升。
- 由于导电区域的连通性,估算的质心不会偏向传感器中心,基于 DNN 的定位结果如图 7 所示
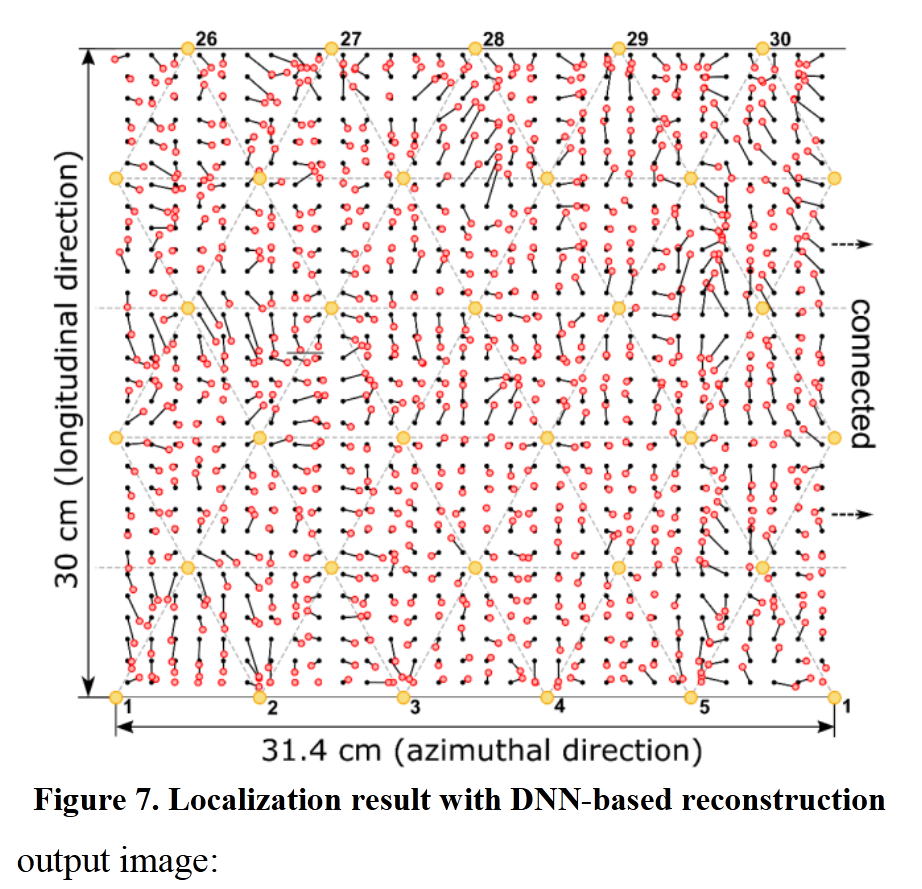
- (图中黑色圆点为压痕位置,红色圆圈为对应的估算位置,黄色圆圈为电极位置,且图的左右边缘在圆柱面上是相连的)。
(三)灵敏度波动
传感器电压变化幅度由压痕位置的电流密度决定,而电流密度随位置和驱动模式变化,导致传感器灵敏度存在波动。为解决这一问题,本文采用 DNN 方法,并与正则化方法进行对比。
- 对于在位置 (i,j) 处压痕得到的输出图像\(I_{i,j}\),根据公式\(C_{i,j}=\frac{max \left(I_{i,j}\right)}{F_{i,j}}\)(i,j=1,...,30,\(max(I_{i,j})\)为重建图像峰值,\(F_{i,j}\)为实测力值)计算灵敏度分布\(C_{i,j}\),对应的灵敏度分布如图 8 所示。

- 将灵敏度分布的标准差相对于平均灵敏度进行归一化后,基于 DNN 方法和正则化方法的标准分布分别为 0.39 和 0.45,表明基于 DNN 的重建方法能使传感器灵敏度分布更均匀。
(四)图像重建结果
压痕实验仅考虑单点压痕情况,而当传感器同时在多个位置受到压痕时,由于传感器的非线性特性,重建图像会出现模糊和失真。为验证 DNN 方法的优势,手动在传感器四个位置同时进行压痕操作,获取测量数据并转换为热图图像,结果如图 9 所示(图中红色圆点为压痕位置)。
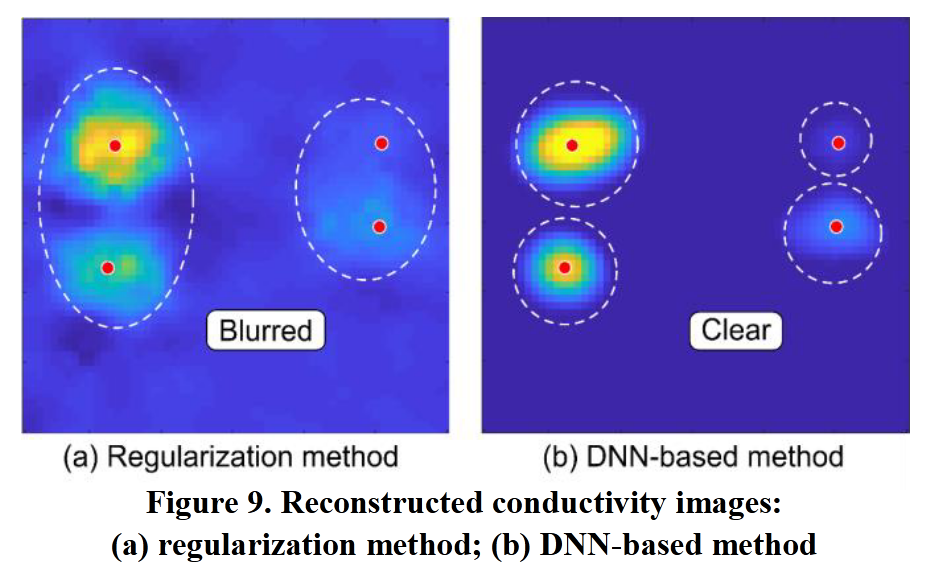
- 图 9(a)为采用线性方法(正则化)重建的图像,图像模糊且噪声大,难以区分各个压痕位置。
- 图 9(b)为基于 DNN 方法重建的图像,图像更清晰,能清楚区分每个扰动位置。这是因为神经网络能部分补偿传感器的非线性行为,也从定性角度表明基于 DNN 的方法可提高传感器的空间分辨率(两点辨别能力)。
五、讨论与结论
本文提出了一种基于 ERT 的稀疏电极机器人皮肤,详细介绍了其设计、制造以及基于 DNN 的信号处理(图像重建)方法。该传感器的电极用于电流注入和电压测量,稀疏分布且牢固嵌入传感器内部,电线不直接暴露在外,具有较强的稳健性且结构简洁。通过喷涂 CNT 分散溶液形成基础导电区域,可在任意曲面上构建导电区域,同时采用高导电织物贴片在感应区域形成压阻结构。传感器结构简单、耐用且可定制,有望集成到商用机器人手臂中。
通过旋转压痕实验装置对传感器和神经网络性能进行评估,结果显示基于 DNN 方法和正则化方法的定位误差分别为 5.2±3.3mm 和 5.5±3.2mm。考虑到电极数量(30 个)和感应区域尺寸(30cm×31.4cm),该结果较为出色。增加电极数量可能进一步提升性能,但由于线性重建矩阵是通过对单元素扰动模拟得到的雅可比矩阵进行正则化推导而来,两种方法的定位精度相近。
基于实测力值和对应图像峰值对传感器灵敏度进行量化分析,发现 DNN 能部分缓解灵敏度波动,表明基于 ERT 的触觉传感器可通过 DNN 和测量数据进行校准。在多点压痕情况下,基于 DNN 的方法能清晰区分靠近的两个刺激,有效补偿传感器非线性行为,提高传感器空间分辨率。
