小杰深度学习（six）——卷积神经网络——计算机眼中的图象、卷积为什么能识别图象

1.计算机眼中的图像

1.1 像素
在了解计算机如何处理图像之前，需要先了解图像的构成元素。
像素是图像的基本单元，每个像素存储着图像的颜色、亮度和其他特征。
一系列像素组合到一起就形成了完整的图像，在计算机中，图像以像素的形式存在并采用二进制格式进行存储。
根据图像的颜色不同，每个像素可以用不同的二进制数表示。
日常生活中常见的图像是RGB三原色图。
RGB图上的每个点都是由红（R）、绿（G）、蓝（B）三个颜色按照一定比例混合而成的，几乎所有颜色都可以通过这三种颜色按照不同比例调配而成。在计算机中，RGB三种颜色被称为RGB三通道，根据这三个通道存储的像素值，来对应不同的颜色。
例如，在使用“画图”软件进行自定义调色时，其数值单位就是像素。如下图所示：

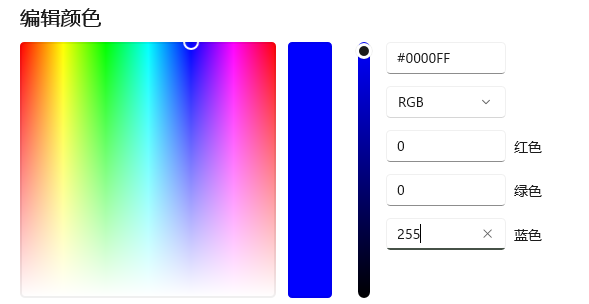
1.2图片输入
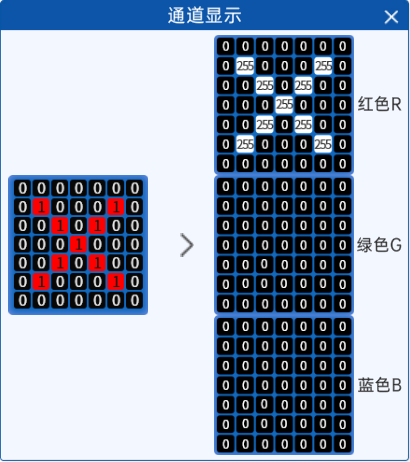
在彩色这个图像中，它分成RGB三通道之后，每个通道都有一个像素的表述，原始的彩色图是一个7*7的，横的7个像素，纵的7个像素，如果把它拆成RGB三个通道之后呢，它依然是一个7*7的像素，一共49个像素点，但是在每个像素值里面，它的范围都是0到255。那么这个彩色图它有一个红色的X，表示红色这个通道对应的位置是255，剩下的是0,而G和B通道呢，他们所有的像素点全都是0，在RGB合并的时候，可以简单的看作是所占的权重比，对于当前彩色图，红色占比最大表现出来的红色X。

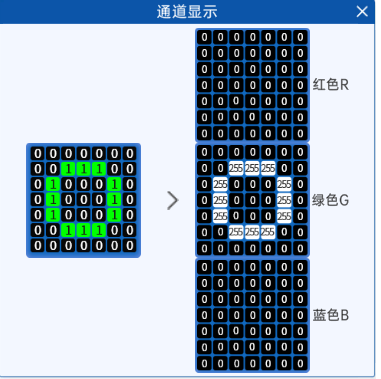
如果是一个绿色的O呢？意味着啥？意味着红色对应的O的位置和蓝色对应O的位置。在绿色位置就是255
，那么两个颜色或者三个颜色是可以组合的。比如红色和绿色它会组成黄色。像素值不能有小数，比如65.2这样的数值。如果在程序中出现小数会报错，但是在有些软件中比如PS这种软件中，可以有小数点，但咱这里不能有小数。在了解了这个通道和像素之后，大家注意，在图上显示的是0~1是为什么？
是因为在很多情况下，会发现它有一个过程叫归一化，很多时候图像像素从0~255归一化到0~1,也就是所有的值都除以255。比如0除以255是0 ，255除以255就是1。图像上显示的0和1是归一化后结果。在很多实际中也会把图像进行归一化。在实际的图像的一个表达中，或者计算机中，实际是0~255，在程序中都归一化到0~1，大家注意一下这个。

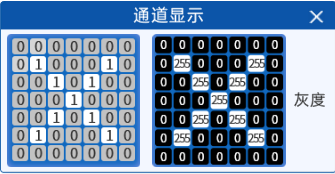
彩色图是这样，灰度图更简单，灰度图它只有一个通道了，灰度图、二值化图都只有一个通道，那这一个通道呢
比如它现在是个X。0代表是黑色，255代表的是白色，介于中间的就是灰色。这里是灰度图

这里本来是0~255变成0~1进行了归一化。
二值化图呢，是0或255 没有中间值，在进行OpenCV处理时灰度图二值化图有个
BINARY阈值或者自适应阈值，要不是白色，要不是黑色，它没有中间灰色，二值化图
只有0或255，归一化后为0或1.
简单过了一下计算机眼中的视觉，这些知识点需要给大家再巩固一下。，因为后面讲卷积的时候要把它当做基础了 ，需要了解卷积的过程而不是图像的过程。

2.卷积为什么能识别图像

1. 基础原理
1.1 卷积的概念
卷积其实是数学中的一种非常复杂的一种运算。但是在计算机中，卷积是指用一个小的卷积核与目标图像进行相乘相加计算，从而提取目标图像中的某些特征，比如边缘、角点等。
1.2 卷积核的概念
卷积核是卷积运算过程中必不可少的一个“工具”，在卷积神经网络中，卷积核是非常重要的，它们被用来提取图像中的特征。
卷积核其实是一个小矩阵，在定义时需要考虑以下几方面的内容：
●卷积核的个数。卷积核的个数决定了其输出特征矩阵的通道数。
●卷积核的值。卷积核的值是自定义的，根据想要提取的特征来进行设置的，后续进行更新。
●卷积核的大小。常见的卷积核有1x1、3x3、5x5等，注意一般都是奇数x奇数。
下图就是一个3x3的卷积核：

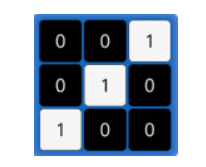
2. 卷积的过程
卷积的过程是将卷积核在图像上进行滑动计算，每次滑动到一个新的位置时，卷积核和图像进行相乘的计算，并将其求和得到一个新的值，然后将这个新的值加入到特征图中，最终得到一个新的特征图。

在这个组件里可以看到padding方式还有步长(strides)。
下面看一下步长和填充方式。
2.1步长
步长就是卷积核在进行完一次卷积操作后卷积核移动的长度。
上面的卷积过程中，步长为1，也就是在进行一次卷积操作后，卷积核会向右（或向下）移动一个单位
而当步长为2时，经过卷积后的结果将会是一个2x2的矩阵，如下图所示：

步长总结：
如果是步长为S=1 输入5*5的图像，输出为3*3的图像
如果步长为S=2,输入5*5的图像，输出为2*2的图像
那么就是说，步长会影响输出的特征图的大小(长和高或者宽和高)
虽然提取的特征依然还是正确的，但是会使得输出特征矩阵变小。

卷积步长代码

#导入包
import torch
import torch.nn as nn
#nn.Sequential 是容器 自带forward方法
conv1_layer=nn.Sequential(nn.Conv2d(in_channels=3,out_channels=3,kernel_size=3,stride=1,bias=False)
)# class convmodel(nn.Module):
#     def __init__(self):
#         super(convmodel,self).__init__()
#         self.conv1_layer=nn.Conv2d(in_channels=3, out_channels=5, kernel_size=3, stride=1, bias=False)
#     def forward(self,x):
#         return self.conv1_layer(x)#仿真  1张3通道的图片
#torch.rand(2,3,30,30)中的第一个2表示样本数量=2,3表示通道数，长 宽为30x30
image=torch.rand(2,3,5,5)
#卷积进行计算
result1=conv1_layer(image)# model=convmodel()
# result2=model(image)
print(result1.shape)
# print(result2.shape)

2.2Padding

Padding，顾名思义，是填充的意思，
它是卷积过程中的一种操作，对原始的输入特征进行处理，用于在图像的边缘添加一些额外的像素，以使得图像的尺寸达到指定的大小。

通常使用填充（Padding）操作来增加图像的大小，以便在应用卷积操作时保持输出特征图的大小与输入特征图相同或更接近。

下面讲解一下Padding填充方式。

2.2.1 int/tuple

padding=int/tuple

举个例子，padding 等于 1 就是补一圈的零，等于 2 就是补两圈的零，如下图所示：

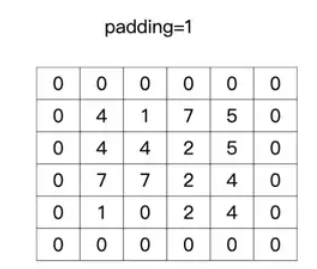
• int：表示2个维度补齐一样多的0
• tuple：按照tuple里的顺序分别给不同方向补齐对应的0（当为 tuple 类型时，第一个维度用于 height 的信息，第二个维度时用于 width 的信息）

2.2.2 VALID

在“VALID”模式下，输入特征图没有补0操作(不改变输入特征图的大小和尺寸)对于5x5的输入特征图和3x3的卷积核，在“VALID”模式下的卷积如下进行：

1. 不进行补0操作：在“VALID”模式下，不对输入特征图进行补0。
2. 计算输出特征图大小： 在“VALID”模式下，输出特征图的大小由以下公式确定：

• 计算方式1(常用)：(输入特征图大小 - 卷积核尺寸 + 2 * P) / 步长 + 1，P是填充0的数量。
• 如果分子除以分母不是整数的话向下取整。

例如：5x5的输入，3x3的卷积核，步长为3，结果是1x1，（5-3）/3+1=1。

• 计算方式2：(输入特征图大小 - 卷积核尺寸 + 1) / 步长
• 如果分子除以分母不是整数的话向上取整。

例如：5x5的输入，3x3的卷积核，步长为2，结果是1x1，（5-3+1）/2=2。

• 两种计算方式是等价的。

2.2.3 SAME

表示在卷积操作中进行填充（补0）操作，但是注意，补多少零不是随便定的，它的目的就是为了让它的输出特征图大小等于输入特征图大小。

输入的特征图大小等于输出的特征图大小的前提是步长等于1(Strides=1)，步长等于1才会这样，步长为2的时候就不这样了。

在使用“SAME”方式进行卷积时，对于5x5的输入特征和3x3的卷积核，补0的方式如下：

输出特征图的大小的计算公式为：

• 输出特征图的大小=(输入特征图大小 - 卷积核尺寸 + 2 * P) / 步长 + 1 向下取整，
• P是填充0的数量(是填充多少层0)，补零规则，补零先补右和下(一层)，然后补左和上(一层)

补零的数量不用计算，只知道如何补零就行，因为pytorch或者tensorflow等框架都实现了。

图中深灰色部分即为补0的部分。

卷积的填充代码

#导入包
import torch
import torch.nn as nn
#nn.Sequential 是容器 自带forward方法
conv1_layer=nn.Sequential(nn.Conv2d(in_channels=3,out_channels=3,kernel_size=3,stride=1,padding='same',bias=False)
)# class convmodel(nn.Module):
#     def __init__(self):
#         super(convmodel,self).__init__()
#         self.conv1_layer=nn.Conv2d(in_channels=3, out_channels=5, kernel_size=3, stride=1, bias=False)
#     def forward(self,x):
#         return self.conv1_layer(x)#仿真  1张3通道的图片
#torch.rand(2,3,30,30)中的第一个2表示样本数量=2,3表示通道数，长 宽为30x30
image=torch.rand(2,3,7,7)
#卷积进行计算
result1=conv1_layer(image)# model=convmodel()
# result2=model(image)
print(result1.shape)
# print(result2.shape)

2.2.3卷积核为什么总是选择奇数大小

在深度学习中，卷积核的大小一般选择奇数是为了方便处理和避免引入不必要的对称性。

当卷积核的大小是奇数时，它具有唯一的一个中心像素，这个中心像素点可以作为滑动的默认参考点，即锚点。

这使得在进行卷积操作时，卷积核可以在输入图像的每个像素周围均匀地取样。这样的好处是，在进行卷积操作时，可以保持对称地处理图像的每个位置，从而避免引入额外的偏差和不对称性。相反，如果卷积核的大小是偶数，那么在某些位置上，中心像素会落在两个相邻的像素之间，这可能导致对称性问题。

此外，选择奇数大小的卷积核还有一个重要的优点是，在进行空间卷积时，可以确保卷积核有一个明确的中心像素，这有助于处理图像的边缘和边界像素，避免模糊和信息损失。

当然，并不是所有情况下都必须选择奇数大小的卷积核。在某些特定情况下，偶数大小的卷积核也可以使用，并且在某些特定任务中可能表现得更好。但是在大多数情况下，奇数大小的卷积核是一种常见且推荐的选择，因为它可以简化卷积操作，并有助于保持图像处理的对称性和一致性。

代码实现

#导入包
import torch
import torch.nn as nn
#nn.Sequential 是容器 自带forward方法
conv1_layer=nn.Sequential(nn.Conv2d(in_channels=3,out_channels=3,kernel_size=3,stride=1,padding='same',bias=False)
)# class convmodel(nn.Module):
#     def __init__(self):
#         super(convmodel,self).__init__()
#         self.conv1_layer=nn.Conv2d(in_channels=3, out_channels=5, kernel_size=3, stride=1, bias=False)
#     def forward(self,x):
#         return self.conv1_layer(x)#仿真  1张3通道的图片
#torch.rand(2,3,30,30)中的第一个2表示样本数量=2,3表示通道数，长 宽为30x30
image=torch.rand(2,3,7,7)
#卷积进行计算
result1=conv1_layer(image)# model=convmodel()
# result2=model(image)
print(result1.shape)
# print(result2.shape)