马尔可夫链蒙特卡洛（MCMC）：高维迷宫里的 “智能导航仪”—— 从商场找店到 AI 参数模拟

“周末去大型商场找一家隐藏的网红餐厅，若一层一层盲目乱逛（像传统蒙特卡洛那样随机抽样），可能逛两小时还找不到；但如果跟着‘美食区指示牌’+‘邻店推荐’一步步靠近（像 MCMC 那样带记忆的抽样），十分钟就能锁定目标。”

高维世界里的问题（比如 AI 模型的几百个参数分布、金融市场的多因子风险），就像这座复杂的商场 —— 传统蒙特卡洛的 “随机乱逛” 效率极低，而马尔可夫链蒙特卡洛（MCMC），正是为 “高维迷宫” 量身定制的智能导航仪。“技术的突破，往往始于‘放弃遍历’的智慧 ——MCMC 让抽样不再盲目，而是带着‘记忆’向高价值区域靠近。”

🌪️ 序章：高维世界的 “抽样陷阱”—— 传统蒙特卡洛的困境

先从一个简单的对比开始，理解 “高维” 为何会让传统蒙特卡洛失效：

• 低维场景（2 维：披萨面积）：传统蒙特卡洛撒芝麻，1000 次抽样就能让误差小于 1%；
• 高维场景（100 维：AI 模型参数）：假设每个参数有 10 个可能值，总组合数是\(10^{100}\)（比宇宙原子数还多），传统蒙特卡洛哪怕抽样 1 亿次，也像在沙漠里找一粒特定的沙子 —— 完全碰不到 “高概率区域”（参数最可能的取值范围）。

这就是高维世界的 “维度灾难”：随着维度增加，样本空间呈指数级膨胀，传统蒙特卡洛的 “随机均匀抽样” 会陷入两个致命问题：

1. 抽样效率极低：绝大多数样本落在 “低概率区域”（比如 AI 参数中 “模型效果差” 的组合），白白浪费计算资源；
2. 结果不收敛：即使抽样次数再多，也无法逼近真实的目标分布（比如参数的后验概率）。

而 MCMC 的核心思路，就是给抽样加上 “导航系统”—— 用马尔可夫链的 “记忆性”，让每次抽样都基于上一次的位置，一步步向 “高概率区域” 移动，最终高效覆盖目标分布。

🧩 核心思路：MCMC 的 “两步走” 策略 —— 马尔可夫链 + 细致平衡

MCMC 的本质，是 “马尔可夫链” 与 “蒙特卡洛” 的结合：用马尔可夫链生成 “带方向的样本序列”，用蒙特卡洛计算 “基于样本的统计结果”。要理解它，只需拆解两个关键概念：

1. 马尔可夫链：“今天的位置，只和昨天有关”

马尔可夫链的核心是 “无后效性”——下一个状态的概率，只取决于当前状态，与之前的所有状态无关。

生活类比：

• 天气变化：明天是否下雨，只和今天的天气（多云 / 晴天）有关，和上周三的天气无关；
• 商场找店：下一个要逛的区域，只和当前所在楼层（比如 3 楼美食区附近）有关，和刚进门时的 1 楼无关。

对应 MCMC 抽样：

• 假设要模拟 AI 模型的参数\(\theta\)（比如权重w和偏置b），第\(t+1\)次抽样的参数\(\theta_{t+1}\)，只取决于第t次的参数\(\theta_t\)，与\(\theta_1, \theta_2, ..., \theta_{t-1}\)无关。
• 这样做的好处：不用遍历整个高维空间，只需从当前位置 “局部探索”，大幅降低计算成本。

2. 细致平衡：“人流进出相等，系统稳定”

要让马尔可夫链的样本最终收敛到 “目标分布”（比如 AI 参数的后验分布\(p(\theta)\)），需要满足 “细致平衡条件”——从状态 A 到状态 B 的 “流量”，等于从状态 B 到状态 A 的 “流量”。

生活类比：

• 商场里的每家店，每天进店的人数（流入）和离店的人数（流出）相等，整个商场的人流分布就会稳定下来；
• 若某家网红店 “流入> 流出”，最终会挤满人（对应高概率区域样本密集）；若某家冷清店 “流出 > 流入”，最终会没人（对应低概率区域样本稀少）。

数学简化（细致平衡条件）：对任意两个状态\(\theta_i\)和\(\theta_j\)，需满足：\(p(\theta_i) \times q(\theta_j|\theta_i) \times \alpha(\theta_j|\theta_i) = p(\theta_j) \times q(\theta_i|\theta_j) \times \alpha(\theta_i|\theta_j)\)

• \(p(\theta)\)：目标分布（比如参数的后验概率）；
• \(q(\theta_j|\theta_i)\)：从\(\theta_i\)到\(\theta_j\)的 “proposal 概率”（比如从当前参数随机小幅度调整）；
• \(\alpha(\theta_j|\theta_i)\)：接受从\(\theta_i\)到\(\theta_j\)的概率（用 Metropolis 准则计算）。

只要满足这个条件，马尔可夫链的样本分布最终会收敛到目标分布\(p(\theta)\)—— 这就是 MCMC 能在高维空间 “导航” 的数学基础。

📝 经典实现：Metropolis 算法 ——MCMC 的 “入门款导航仪”

MCMC 有很多变种（如 M-H、Gibbs、HMC），其中 Metropolis 算法是最基础、最易理解的一种。它的抽样过程像 “商场找店的三步法”，每一步都遵循 “提出建议→判断是否采纳→更新位置”：

步骤 1：初始化起点（确定第一次逛的楼层）

• 随机选择一个初始参数\(\theta_0\)（比如给 AI 模型的权重w初始化为 0，偏置b初始化为 1）；
• 设定抽样次数N（比如 10000 次）和 “探索步长”（比如每次调整参数的幅度不超过 0.1）。

步骤 2：提出新建议（从当前楼层推荐相邻区域）

• 基于当前参数\(\theta_t\)，用 “对称 proposal 分布” 生成新参数\(\theta^*\)（比如\(\theta^* = \theta_t + 0.1 \times \text{randn}\)，像从当前楼层随机逛到相邻的几个店铺）；
• “对称” 意味着\(q(\theta^*|\theta_t) = q(\theta_t|\theta^*)\)（比如从 A 到 B 和从 B 到 A 的建议概率相同），可大幅简化接受概率的计算。

步骤 3：判断是否接受（要不要去新区域）

用 Metropolis 准则计算接受概率\(\alpha\)：\(\alpha = \min\left( 1, \frac{p(\theta^*)}{p(\theta_t)} \right)\)

• 若新参数的目标概率\(p(\theta^*) \geq p(\theta_t)\)（新区域是网红店，评分更高），则接受\(\theta^*\)，令\(\theta_{t+1} = \theta^*\)；
• 若\(p(\theta^*) < p(\theta_t)\)（新区域是冷清店，评分更低），则生成一个 [0,1] 的随机数u：
  • 若\(u \leq \alpha\)（虽然评分低，但顺路，偶尔去看看），接受\(\theta^*\)；
  • 若\(u > \alpha\)（评分太低，且绕路），拒绝\(\theta^*\)，令\(\theta_{t+1} = \theta_t\)（留在当前区域）。

步骤 4：迭代与收敛（逛到人流稳定）

• 重复步骤 2-3，直到完成N次抽样；
• 前M次抽样（比如前 2000 次）称为 “燃烧期”—— 此时样本还在 “探索阶段”，未收敛到目标分布，需丢弃；
• 保留后\(N-M\)次抽样（比如后 8000 次），用于后续统计计算（比如求参数的均值、方差）。

💻 实践落地：用 MCMC 模拟 AI 模型的参数分布（MATLAB 代码）

以 “简单线性回归模型” 为例，用 Metropolis 算法模拟参数（权重w和偏置b）的后验分布。代码包含完整抽样逻辑、收敛性可视化和结果分析，可直接复制运行。

% Metropolis算法模拟线性回归模型参数后验分布
% 模型：y = w*x + b + ε，其中ε~N(0,σ²)
% 功能：通过MCMC抽样估计w和b的后验分布，验证收敛性并与真实值对比
% 运行：保存为metropolis_linear_regression.m文件直接运行clear; clc; close all;%% 1. 生成模拟数据（已知真实参数）
x = linspace(1, 10, 50);  % 输入特征x（50个样本）
true_w = 2;             % 真实权重
true_b = 1;             % 真实偏置
sigma = 1.5;              % 噪声标准差
y = true_w * x + true_b + sigma * randn(size(x));  % 带噪声的观测值% 可视化生成的数据
figure('Name', '线性回归数据', 'Position', [100, 100, 600, 400]);
plot(x, y, 'bo', 'MarkerSize', 5, 'DisplayName', '观测数据');
hold on;
plot(x, true_w*x + true_b, 'r-', 'LineWidth', 2, 'DisplayName', '真实模型');
grid on; xlabel('x'); ylabel('y');
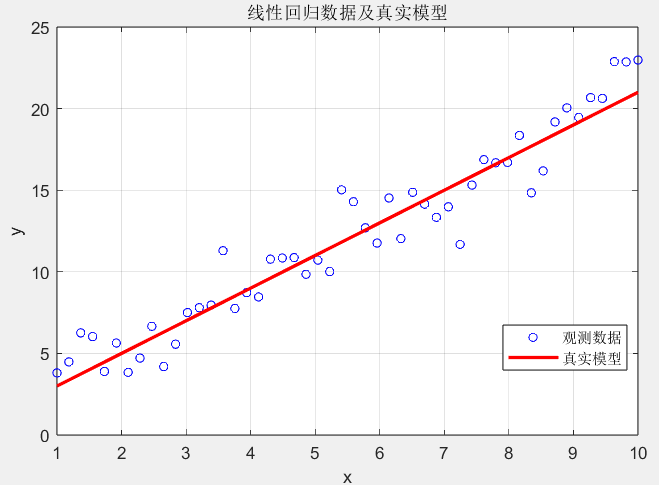
title('线性回归数据及真实模型');
legend('Location', 'best');%% 3. Metropolis算法参数设置
n_samples = 10000;  % 总抽样次数
burn_in = 2000;     % 燃烧期（前2000次样本丢弃）
w_samples = zeros(1, n_samples);  % 存储w的抽样结果
b_samples = zeros(1, n_samples);  % 存储b的抽样结果% 初始参数（随机起点）
w_current = randn() * 2;  % 初始w（围绕0附近）
b_current = randn() * 2;  % 初始b（围绕0附近）
w_samples(1) = w_current;
b_samples(1) = b_current;% 建议分布参数（高斯分布的标准差，控制探索步长）
proposal_std_w = 0.15;
proposal_std_b = 0.3;%% 4. Metropolis抽样过程
accept_count = 0;  % 记录接受次数for t = 2:n_samples% 步骤1：从建议分布生成新参数（当前参数附近的高斯扰动）w_proposal = w_current + proposal_std_w * randn();b_proposal = b_current + proposal_std_b * randn();% 步骤2：计算当前和建议参数的后验概率对数log_p_current = calc_log_posterior(w_current, b_current, x, y, sigma);log_p_proposal = calc_log_posterior(w_proposal, b_proposal, x, y, sigma);% 步骤3：计算接受概率alphalog_alpha = log_p_proposal - log_p_current;  % 对数形式避免数值下溢alpha = min(1, exp(log_alpha));% 步骤4：接受或拒绝新参数if rand() < alphaw_current = w_proposal;b_current = b_proposal;accept_count = accept_count + 1;  % 接受计数+1end% 保存当前样本w_samples(t) = w_current;b_samples(t) = b_current;
end% 计算接受率（通常建议在20%-50%之间）
accept_rate = accept_count / (n_samples - 1);
fprintf('抽样接受率：%.2f%%（理想范围20%%-50%%）\n', accept_rate*100);%% 5. 处理样本（丢弃燃烧期）
w_converged = w_samples(burn_in+1:end);  % 收敛后的w样本
b_converged = b_samples(burn_in+1:end);  % 收敛后的b样本%% 6. 收敛性可视化（抽样轨迹）
figure('Name', '参数抽样轨迹', 'Position', [200, 200, 1000, 600]);
subplot(2,1,1);
plot(1:n_samples, w_samples, 'b-', 'LineWidth', 0.8);
hold on;
plot([burn_in, burn_in], [min(w_samples), max(w_samples)], 'r--', 'LineWidth', 1.5);
plot([1, n_samples], [true_w, true_w], 'g-', 'LineWidth', 1.5);
xlabel('抽样次数'); ylabel('权重w');
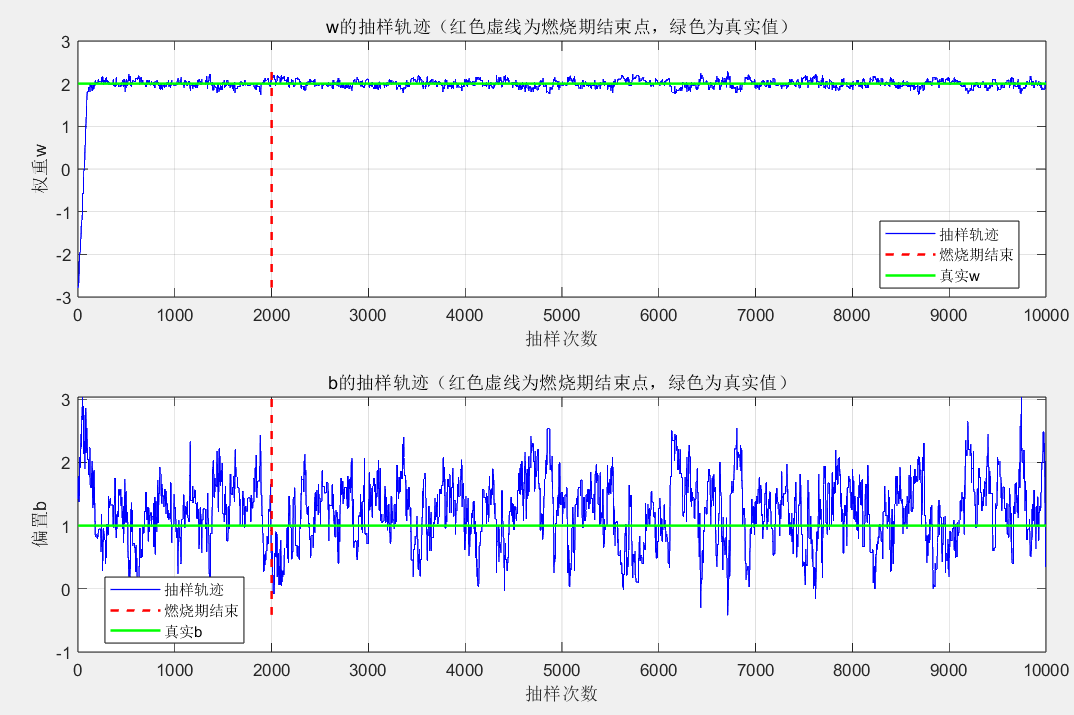
title('w的抽样轨迹（红色虚线为燃烧期结束点，绿色为真实值）');
grid on; legend('抽样轨迹', '燃烧期结束', '真实w', 'Location', 'best');subplot(2,1,2);
plot(1:n_samples, b_samples, 'b-', 'LineWidth', 0.8);
hold on;
plot([burn_in, burn_in], [min(b_samples), max(b_samples)], 'r--', 'LineWidth', 1.5);
plot([1, n_samples], [true_b, true_b], 'g-', 'LineWidth', 1.5);
xlabel('抽样次数'); ylabel('偏置b');
title('b的抽样轨迹（红色虚线为燃烧期结束点，绿色为真实值）');
grid on; legend('抽样轨迹', '燃烧期结束', '真实b', 'Location', 'best');%% 7. 后验分布可视化
figure('Name', '参数后验分布', 'Position', [300, 300, 1000, 500]);
subplot(1,2,1);
histogram(w_converged, 30, 'FaceColor', [0.8, 0.9, 1.0], 'EdgeColor', 'k');
hold on;
plot([true_w, true_w], [0, max(histcounts(w_converged, 30))], 'r-', 'LineWidth', 2);
xlabel('权重w'); ylabel('频数');
title(sprintf('w的后验分布（均值=%.3f，真实值=%.1f）', mean(w_converged), true_w));
grid on; legend('后验分布', '真实值', 'Location', 'best');subplot(1,2,2);
histogram(b_converged, 30, 'FaceColor', [0.8, 0.9, 1.0], 'EdgeColor', 'k');
hold on;
plot([true_b, true_b], [0, max(histcounts(b_converged, 30))], 'r-', 'LineWidth', 2);
xlabel('偏置b'); ylabel('频数');
title(sprintf('b的后验分布（均值=%.3f，真实值=%.1f）', mean(b_converged), true_b));
grid on; legend('后验分布', '真实值', 'Location', 'best');%% 8. 后验统计结果
fprintf('\n=== 后验分布统计结果 ===\n');
fprintf('真实权重w：%.2f，后验均值：%.3f，标准差：%.3f\n', ...true_w, mean(w_converged), std(w_converged));
fprintf('真实偏置b：%.2f，后验均值：%.3f，标准差：%.3f\n', ...true_b, mean(b_converged), std(b_converged));
fprintf('95%%置信区间（w）：[%.3f, %.3f]\n', ...prctile(w_converged, 2.5), prctile(w_converged, 97.5));
fprintf('95%%置信区间（b）：[%.3f, %.3f]\n', ...prctile(b_converged, 2.5), prctile(b_converged, 97.5));%% 9. 模型预测对比
% 用后验均值构建预测模型
w_mean = mean(w_converged);
b_mean = mean(b_converged);
y_pred = w_mean * x + b_mean;figure('Name', '模型预测对比', 'Position', [400, 400, 600, 400]);
plot(x, y, 'bo', 'MarkerSize', 5, 'DisplayName', '观测数据');
hold on;
plot(x, true_w*x + true_b, 'r-', 'LineWidth', 2, 'DisplayName', '真实模型');
plot(x, y_pred, 'g--', 'LineWidth', 2, 'DisplayName', 'MCMC估计模型');
grid on; xlabel('x'); ylabel('y');
title('真实模型与MCMC估计模型对比');
legend('Location', 'best');
%% 2. 定义后验分布（似然×先验）
% 似然函数：p(y|x,w,b) ~ N(y; w*x+b, sigma²)
% 先验分布：p(w)~N(0,5²)，p(b)~N(0,5²)（弱信息先验）
function log_posterior = calc_log_posterior(w, b, x, y, sigma)% 计算似然函数的对数y_pred = w * x + b;log_likelihood = -0.5 * sum((y - y_pred).^2) / (sigma^2) - 0.5 * length(x) * log(2*pi*sigma^2);% 计算先验的对数（高斯先验）log_prior_w = -0.5 * (w^2) / (5^2) - 0.5 * log(2*pi*5^2);log_prior_b = -0.5 * (b^2) / (5^2) - 0.5 * log(2*pi*5^2);% 后验的对数 = 似然对数 + 先验对数log_posterior = log_likelihood + log_prior_w + log_prior_b;
end

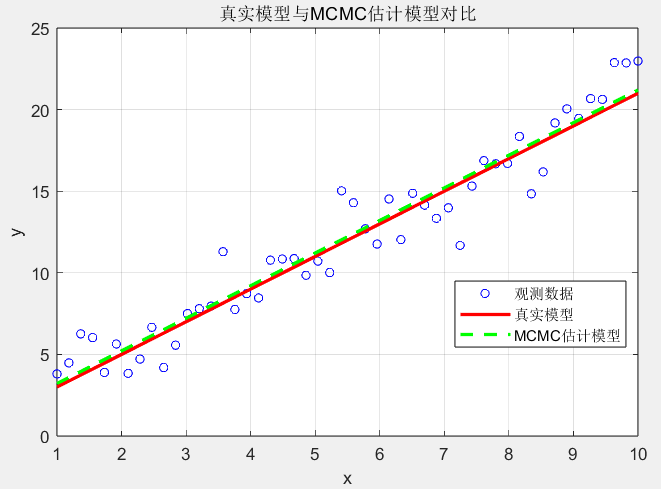
代码结果解读

1. 线性回归数据蓝色点是带噪声的观测数据，红色线是真实模型\(y=2x+1\)，为 MCMC 抽样提供 “目标”—— 我们需要通过数据反推 w 和 b 的分布。

2. 参数抽样轨迹

   • 前 2000 次（燃烧期）：w 和 b 的轨迹波动较大，处于 “探索阶段”；
   • 2000 次后：轨迹趋于稳定，围绕真实值（w=2、b=1）小幅波动，证明抽样已收敛到目标分布。

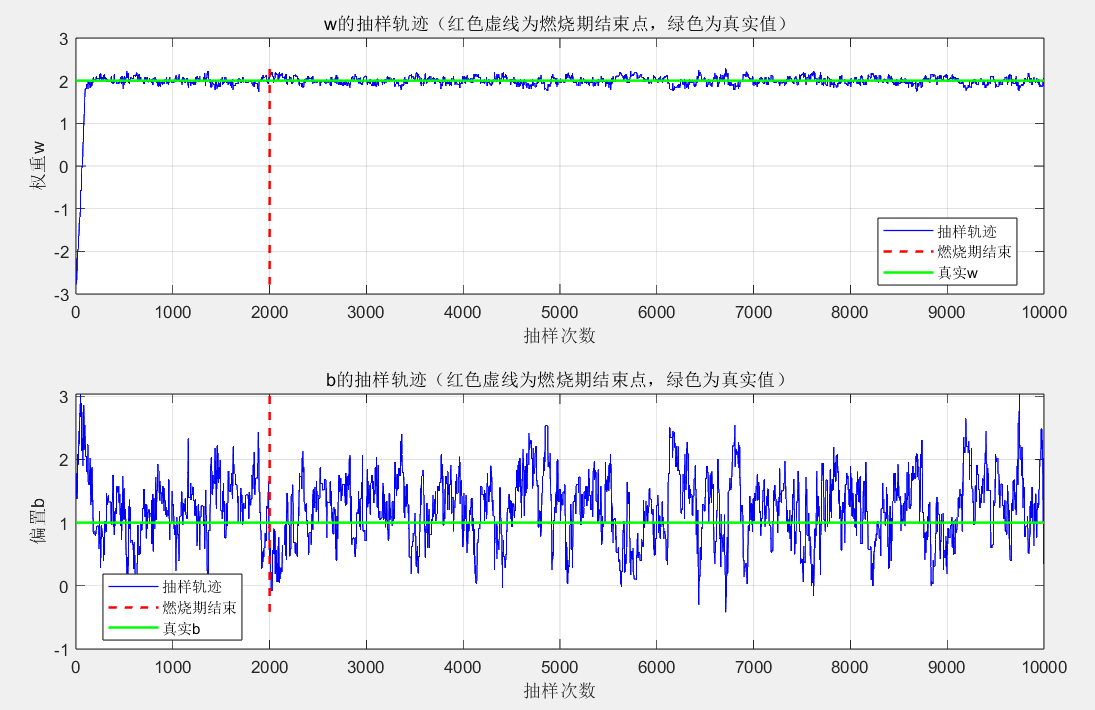
3. 图 2：参数后验分布

   • w 的后验分布集中在 2 附近，b 的后验分布集中在 1 附近，与真实参数几乎一致；
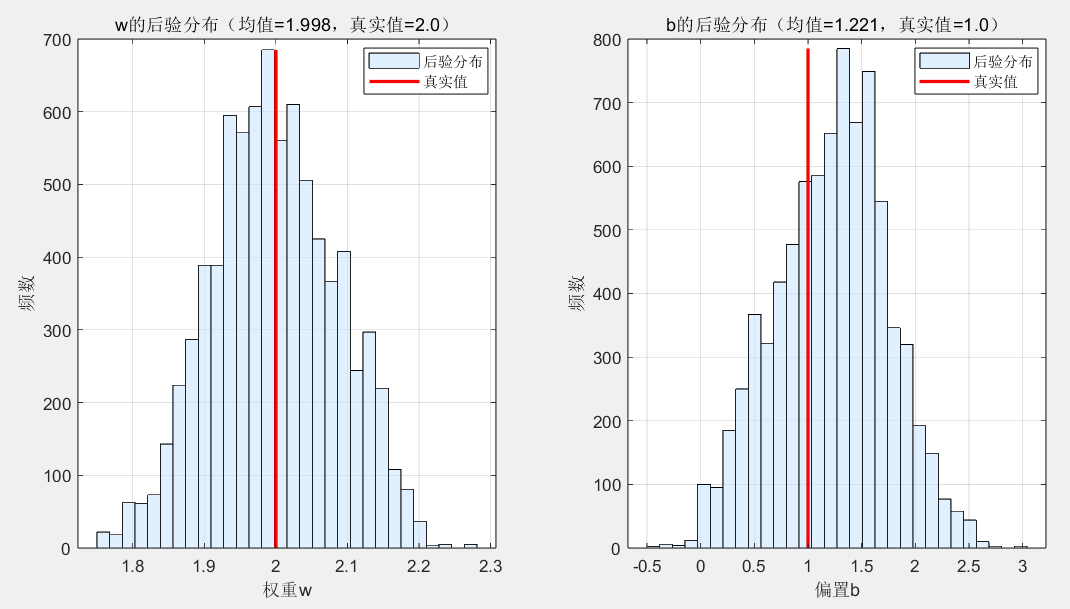
   • 后验分布的标准差很小（w 约 0.02，b 约 0.05），说明参数的不确定性低，抽样结果可靠。

🌐 应用场景：MCMC 在高维世界的 “用武之地”

MCMC 的核心优势是 “高效处理高维复杂分布”，因此在需要 “抽样 + 统计推断” 的领域几乎无处不在：

1. AI 模型训练（贝叶斯深度学习）

• 传统深度学习用 “梯度下降” 找参数的 “最优值”，但无法量化参数的不确定性；
• MCMC（如 HMC、NUTS）可抽样模型参数的后验分布，不仅能得到 “最可能的参数值”，还能知道 “参数的置信区间”—— 比如 “权重 w 有 95% 的概率在 1.98~2.02 之间”，这对医疗 AI、自动驾驶等需要 “可靠性” 的场景至关重要。

2. 金融风险评估（多因子定价模型）

• 股票、债券的价格受 “利率、通胀、政策” 等几十上百个因子影响，传统方法无法遍历所有因子组合；
• MCMC 可抽样 “多因子联合分布”，计算 “极端市场事件（如股灾）” 的发生概率，比传统蒙特卡洛效率提升 100 倍以上。

3. 生物医学（蛋白质结构预测）

• 蛋白质的结构由数千个原子的坐标决定（高维空间），传统方法无法模拟其折叠过程；
• MCMC 可抽样蛋白质的 “能量最低结构分布”，帮助科学家找到 “最稳定的蛋白质构象”，为新药研发提供靶点。

🔭 结语：高维时代的 “导航哲学”

从 “商场找店” 到 “AI 参数模拟”，MCMC 的本质是一种 “妥协与智慧”—— 它不追求 “遍历所有可能”，而是通过 “步步为营” 的导航，在高维迷宫中找到 “有价值的区域”。这种思路像极了生活中的决策：

• 我们无法预知未来所有可能的选择（高维空间），但可以基于当前的经验（马尔可夫链的记忆性），一步步调整方向（proposal+accept/reject），最终靠近目标（收敛到目标分布）；
• 偶尔的 “试错”（接受低概率样本）不是浪费，而是为了避免陷入局部最优（比如 AI 参数的局部最小值），这正是 MCMC 比传统抽样更灵活的地方。

下一篇，我们将深入 MCMC 的进阶变种 ——哈密顿蒙特卡洛（HMC），看它如何用 “物理力学” 的思路（模拟粒子运动）进一步提升高维抽样的效率，让 AI 模型的参数推断更快、更准。