【计算几何 | 数学】向量的妙用(判断线段与圆是否相交 求两条线段交点 点到线段的距离)附例题
前导(为什么要使用向量 & 朴素方法)
在做计算几何的题目时,比起用点到直线的距离公式,
我们会更倾向于使用向量(点积或者叉积)。
1.判断线段与圆是否相交
举个例子,我们需要判断一条线段与圆是否相交,有以下几种情况:
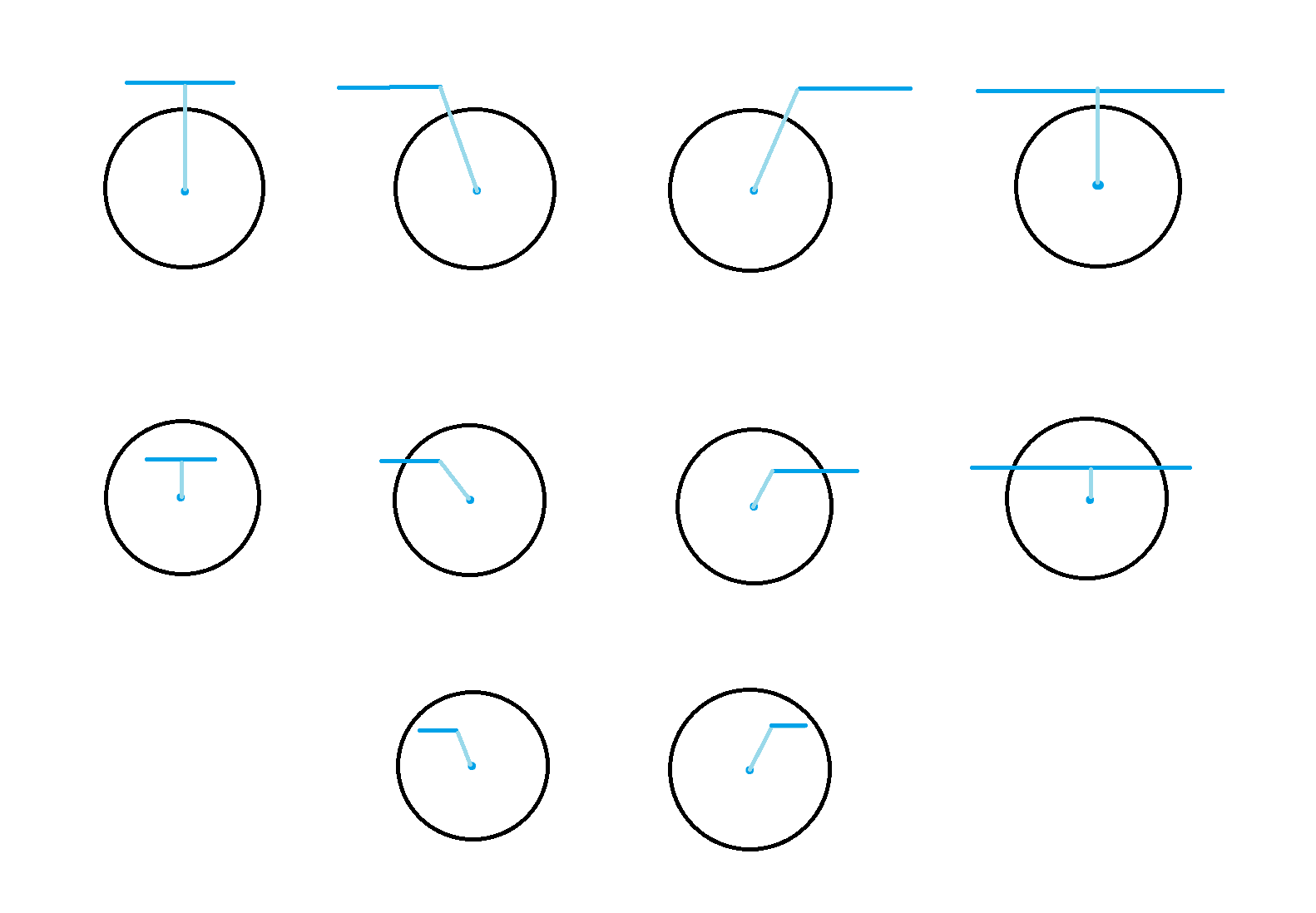
如果不使用向量,我们需要先分类:
(1)线段两端点都在圆外
(2)线段两端点都在圆内
(3)线段一个端点在圆外,另一个端点在圆内
第二种情况是完全相交,直接返回 1,而其它两种情况还要分类:
(1)圆心可以垂直投影到线段
(2)距离圆心最近的点是线段的两端
求出这个线段上距离圆心最近的点到圆心的距离 L,如果 L 小于半径,则线段与圆相交。
可以发现分类分的特别痛苦。
2.求两条线段的交点
再举个例子,求两条线段的交点。
看上去只用代入两条线段所属直线的方程就够了,但是:
(1)数据可能是浮点,要用 exgcd(拓展欧几里得算法)
(2)两条直线的斜率极其接近, 下面的分母会很小,除以的结果会很大,精度丢失
(3)两条直线重合(斜率相减的绝对值小于一个精度阈值),需要特判重合或者平行
求出两条直线的交点后,还要判断这个交点在不在两条线段上。
还是很麻烦。
向量
指路大佬博客(初步了解或者复习):向量、数量积、向量积-CSDN博客
建议所有人都看一下,提前有个底。
1.叉积与面积
我们一般在计算几何提到叉积,不是指数学意义上的三维垂直叉积(下图中的紫色向量)。
而是指图中浅紫色四边形的面积:
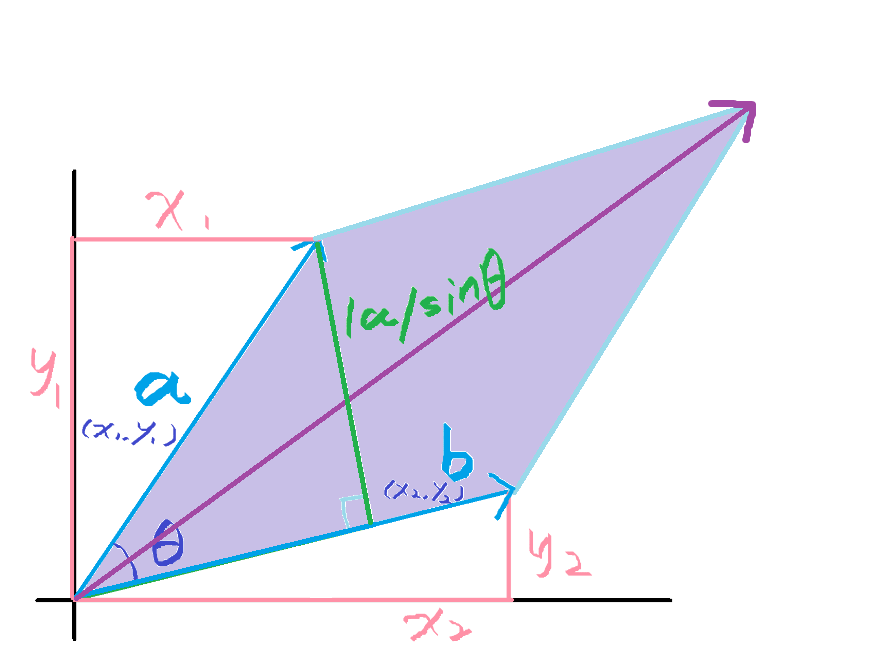
向量 和向量
的叉积写作:
也是:
(其中 为向量
的模长(就是向量的大小 / 长度),
为两向量的夹角)
当叉积小于 ,代表
在
的左边。
当叉积等于 ,当表
和
相等。
当叉积大于 ,代表
在
的右边。
(如图就是 在
的左边,取面积的时候一般取绝对值)
第一个公式很好理解,图中绿色的 是平行四边形的高。
是底,两者相乘就是平行四边形的面积。
那 怎么解释呢?
将平行四边形分割:
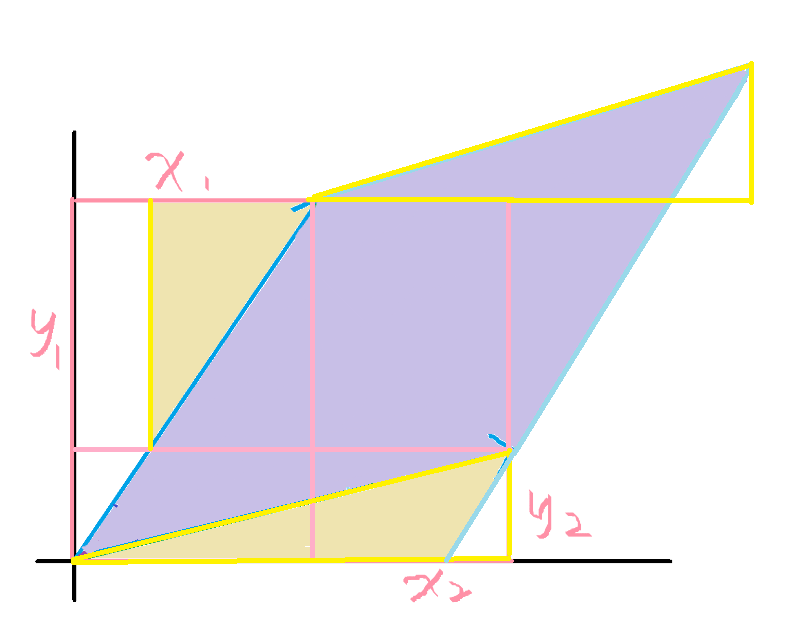
发现上面那个黄色三角形和下面的一模一样,可以移下来。
再把右边多出来的紫色小三角形移到左边,发现剩余的白色区域可以拼出最左边的白色长方形。
这个白色长方形的宽是 ,长是
。
那么整体紫色面积就等于:
说了这么多,只是想你记住:
设向量 的顶点为
,向量
的顶点为
。
那么两个向量的叉积,也就是两者围成的平行四边形的面积(要取绝对值)为:
叉积的正负遵循右手法则:
当叉积小于 ,代表
在
的左边。
当叉积等于 ,当表
和
相等。
当叉积大于 ,代表
在
的右边。
1.5.叉积的运用
回到我们开头举的第二个例子:
求两条线段的交点。
请看,图中深蓝 和红色
的是要计算交点的向量,深紫色
是
的起点到
的起点的向量。
(后面讲这个 有什么作用)
浅蓝是向量 到交点的延长线,粉色是向量
到交点的延长线:
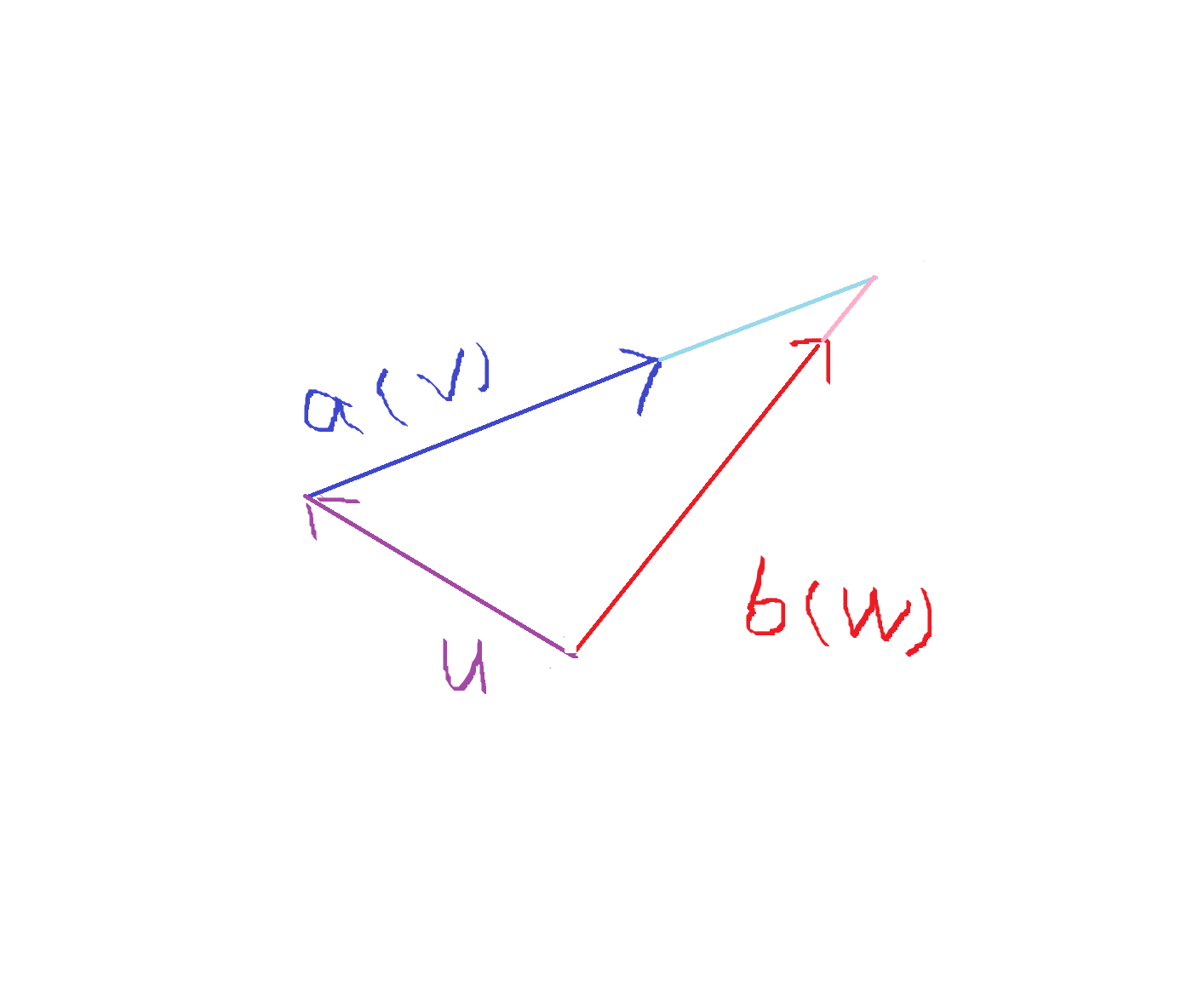
总体思路:
构造出两个同底的平行四边形,通过它们高的比求出斜边的比。
进而求出向量 延长到交点的长度与向量
的模长比。
我们知道叉积的绝对值,就是俩向量构成的平行四边形面积的值,所以也就有:
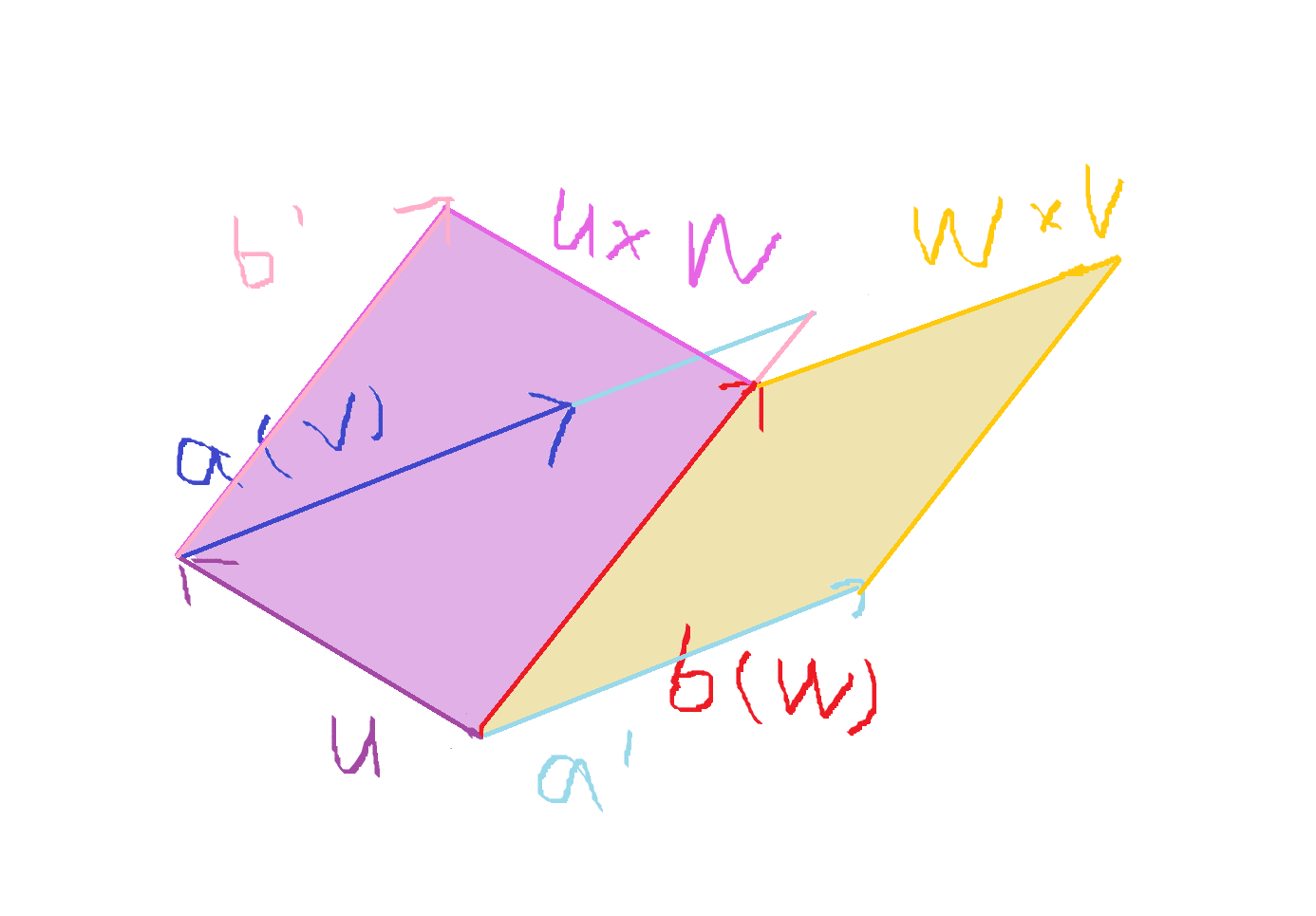
(淡紫色的平行四边形是 ,浅黄色的平行四边形是
)
设 ,也就是俩平行四边形面积比,
又因为俩四边形底相同,所以面积比就是与底相对应的高的比。
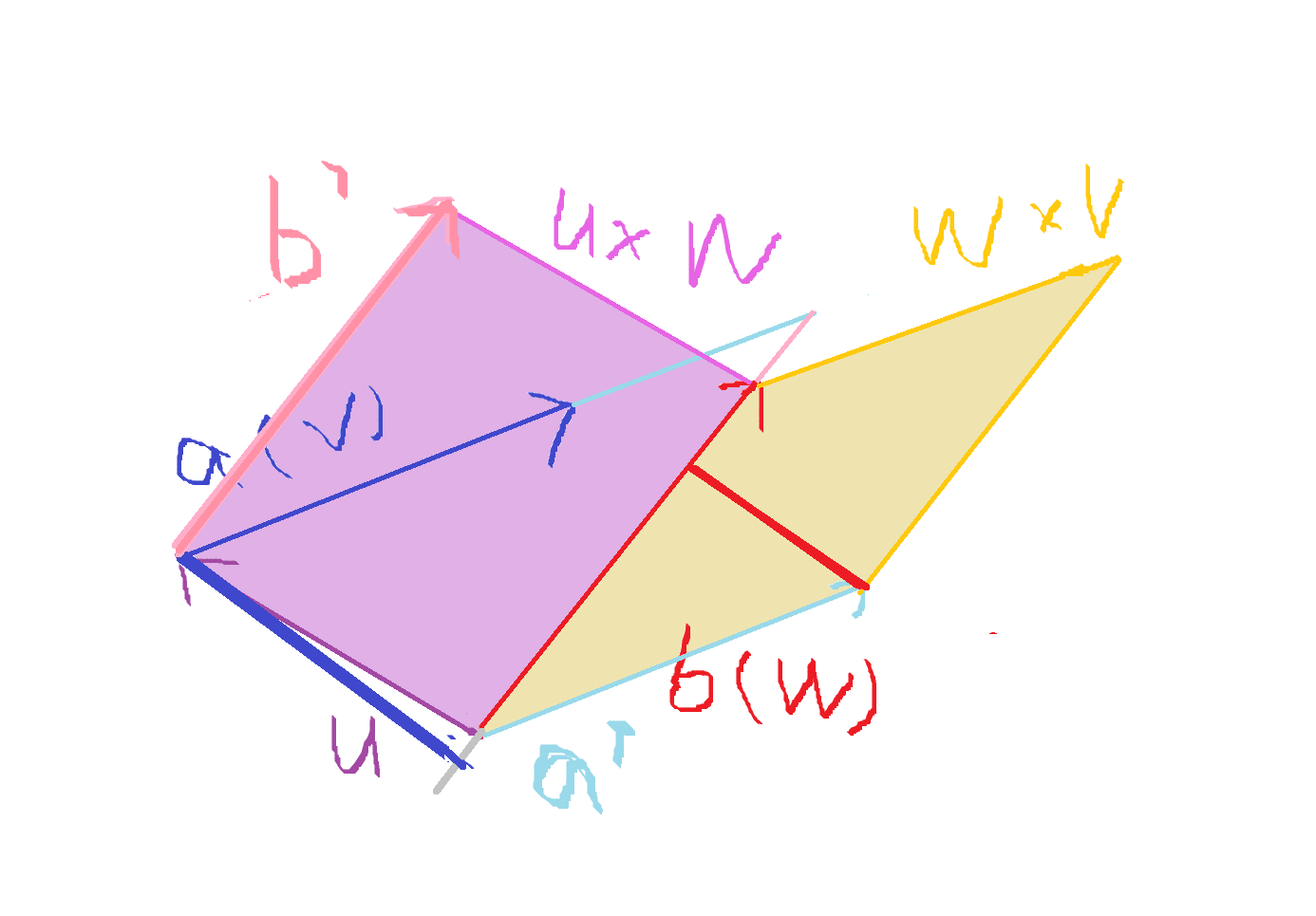
(蓝色加粗的是 的高,红色加粗的是
的高)
我们又发现,因为浅蓝色 等于深蓝色
,
所以可以把那条红色的高平移到粉色 下面,刚好接着向量 的终点:
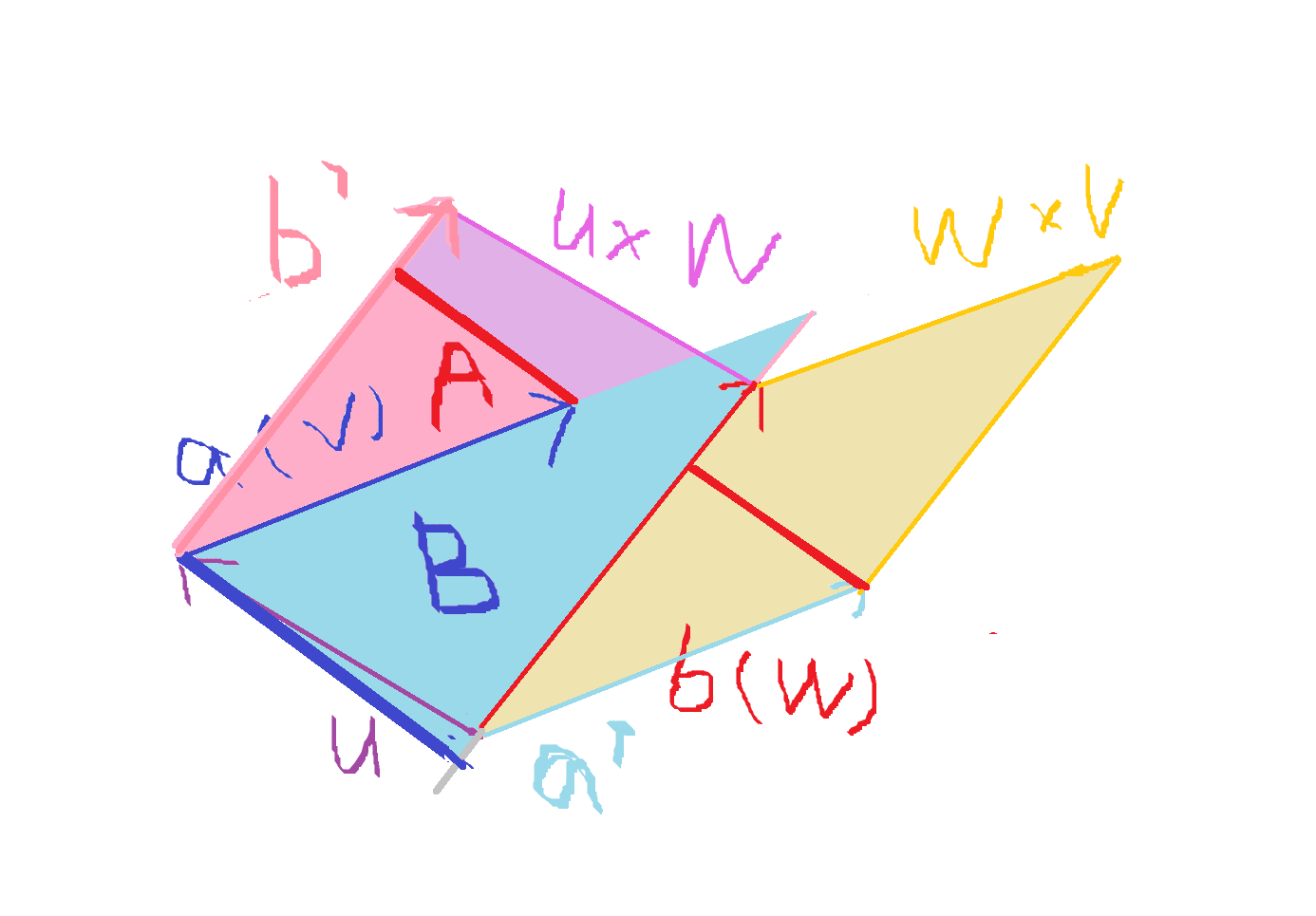
平移过来后,我们发现新构成的俩三角形 和
是相似的,
而它们的高比就等于斜边比,也就是向量 延长到交点的长度与向量
的模长比。
知道了这个比 ,就可以向量
的起点
加上向量
得到交点。
代码:
//以下 operator都是重载运算符
point operator+(point a, point b) { //向量相加 return {a.x + b.x, a.y + b.y};
}point operator-(point a, point b) { //向量相减 return {a.x - b.x, a.y - b.y};
}point operator*(point a, double t) { //向量数乘 return {a.x * t, a.y * t};
}double operator*(point a, point b) { //叉积 return a.x * b.y - a.y * b.x;
}point cross(line a, line b) { //求俩向量交点 point u = a.s - b.s; // b 起点到 a 起点 point v = a.e - a.s; // a 起点到 a 终点 point w = b.e - b.s; // b 起点到 b 终点 double t = (u * w) / (w * v);return a.s + v * t;
}例题:【超多图!笔记】[HNOI2008] 洛谷P3194 水平可见直线 [半平面交]_洛谷b3194-CSDN博客
2.点积与投影
还是这张图:
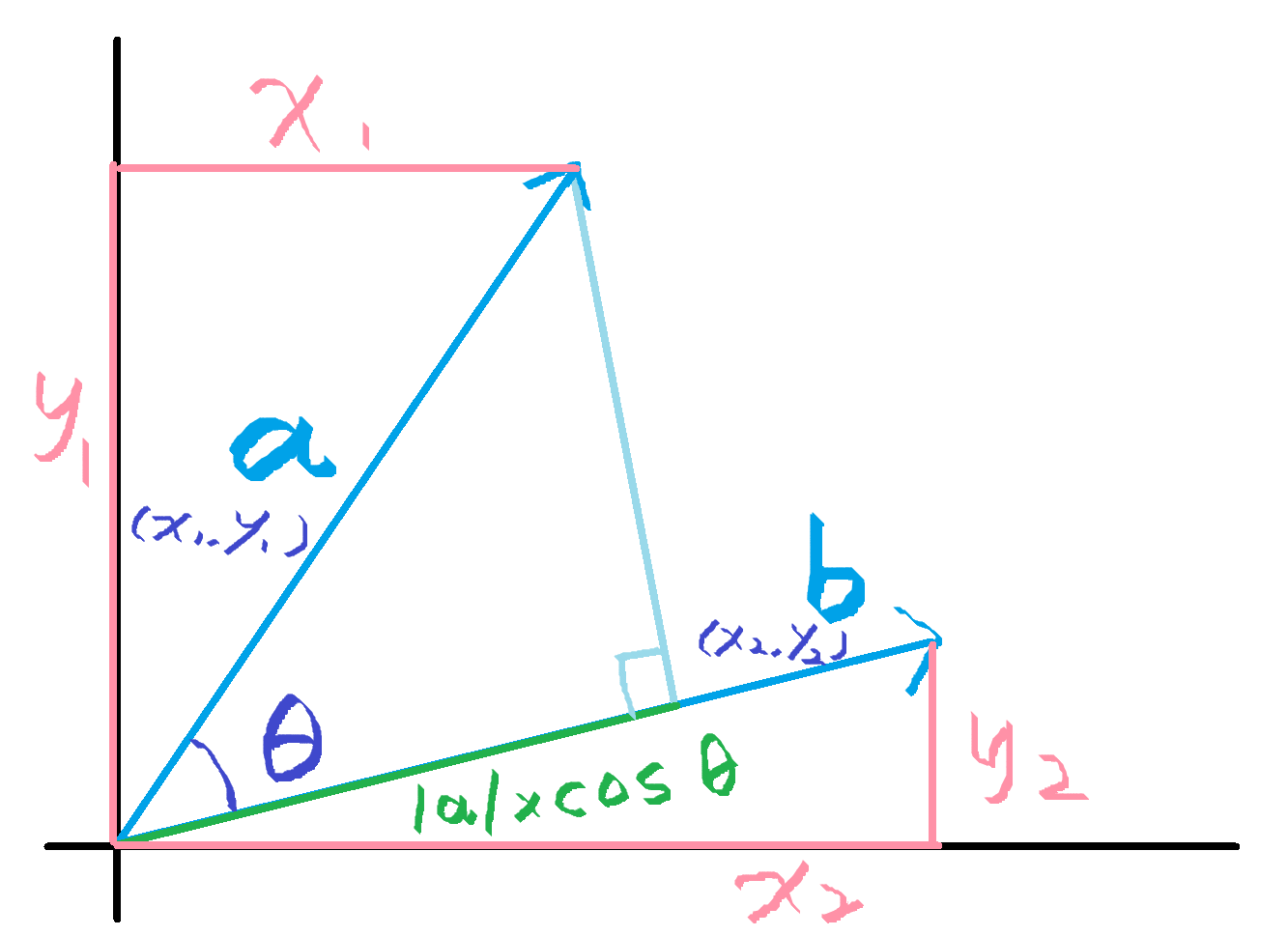
定义两个向量的点积为:
同时几何定义里也可以这么表示:
(点积几何意义:向量 在向量
上的投影长度与
模长之积)
和叉积不同,点积的计算结果是一个标量(数值)而非向量。
这个数值表示向量 和向量
的相似度,数值越大两者越相似。
关于这个 和这个
为什么相等,需要用到余弦定理:
考虑由
、
和
构成的三角形,满足:
(下面就是余弦定理的百度百科,我懒得写了)
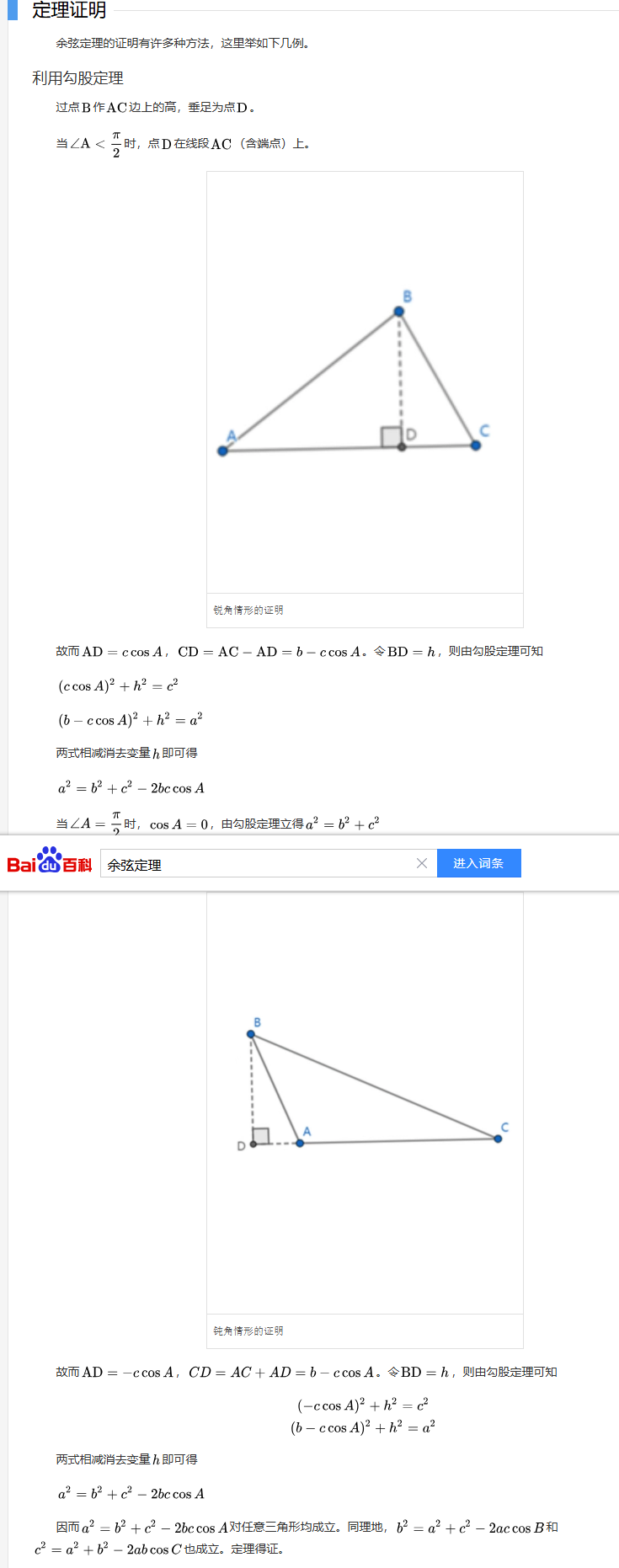
把这个式子的左边展开:
那么就有:
所以:
2.5.点积的运用
求点到直线的距离。
我们想求点 P 到线段 AB 的距离。
如果 P 在 AB 中间:
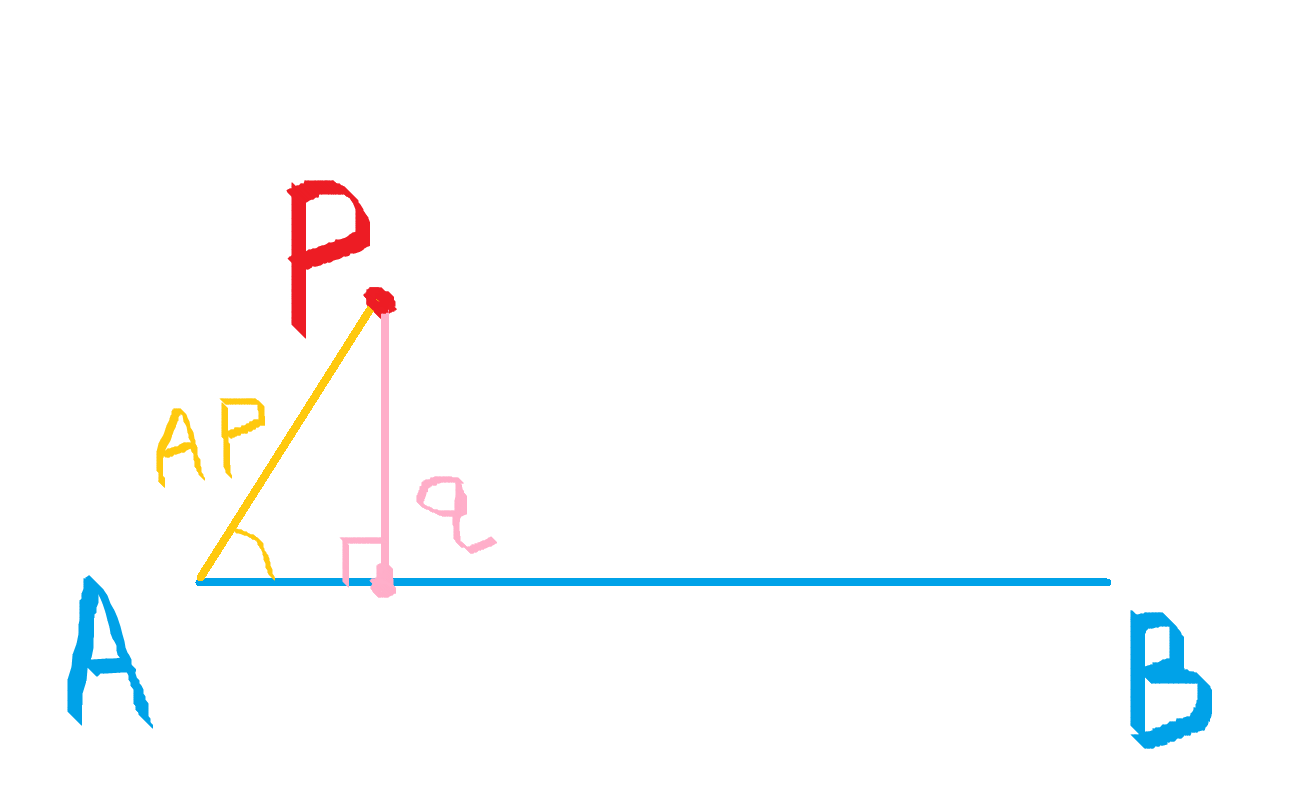
我们只要求出 P 在 AB 上的投影点 q,再求出 Pq 的长度就是距离。
考虑 AP 和 AB 的点积,,其中
就是 Aq 的长度。
那么只要求出 Aq 的长度与 AB 长度的比值 t,就可以进一步求出 Pq。
再看看其他两种情况:
P 在 A 的左边,距离为 PA。
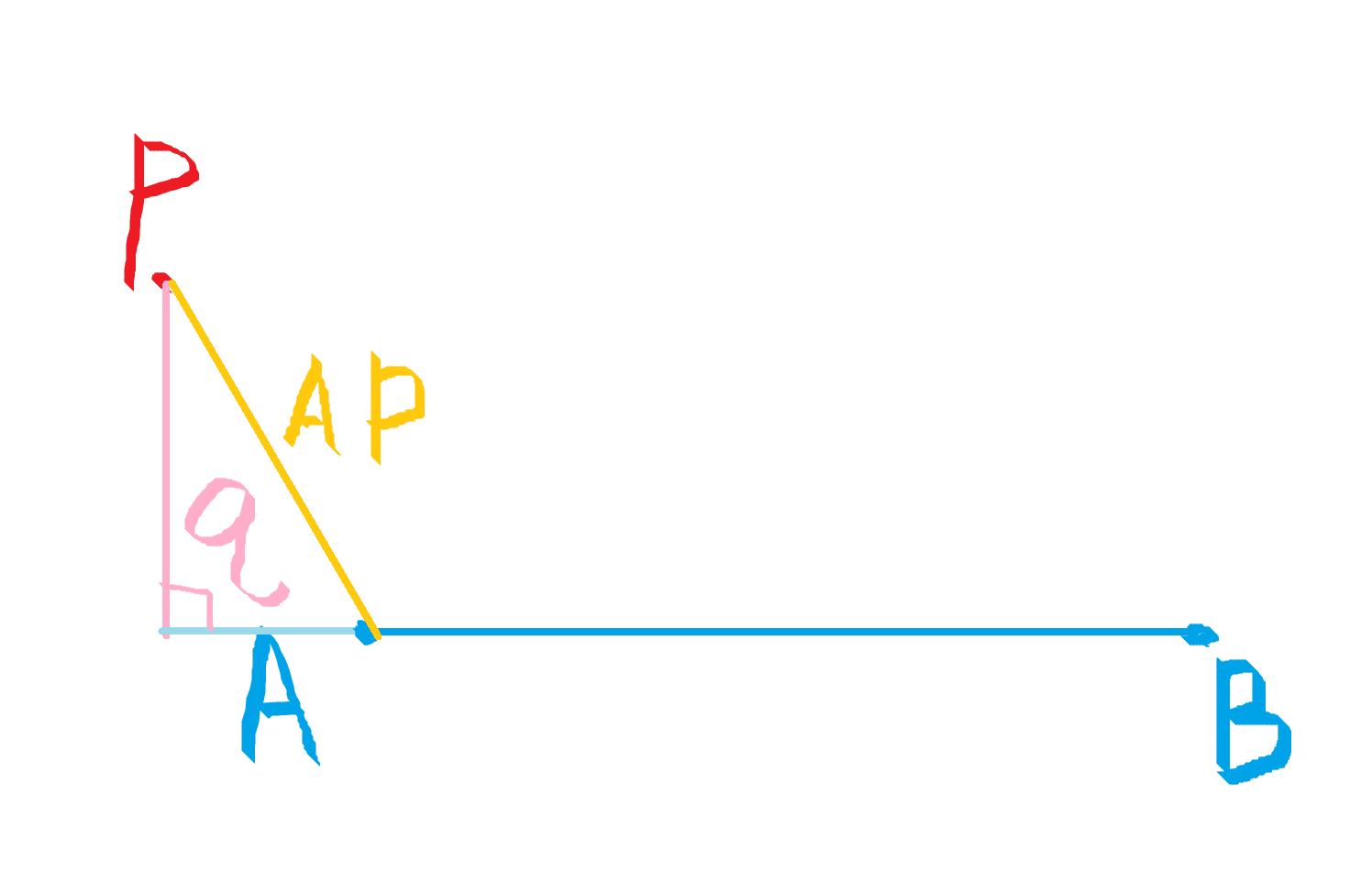
很明显,这里 是个负数,
也是个负数。
那只要特判比值 是不是负数,如果是就直接输出
。
P 在 B 的右边,距离为 PB。
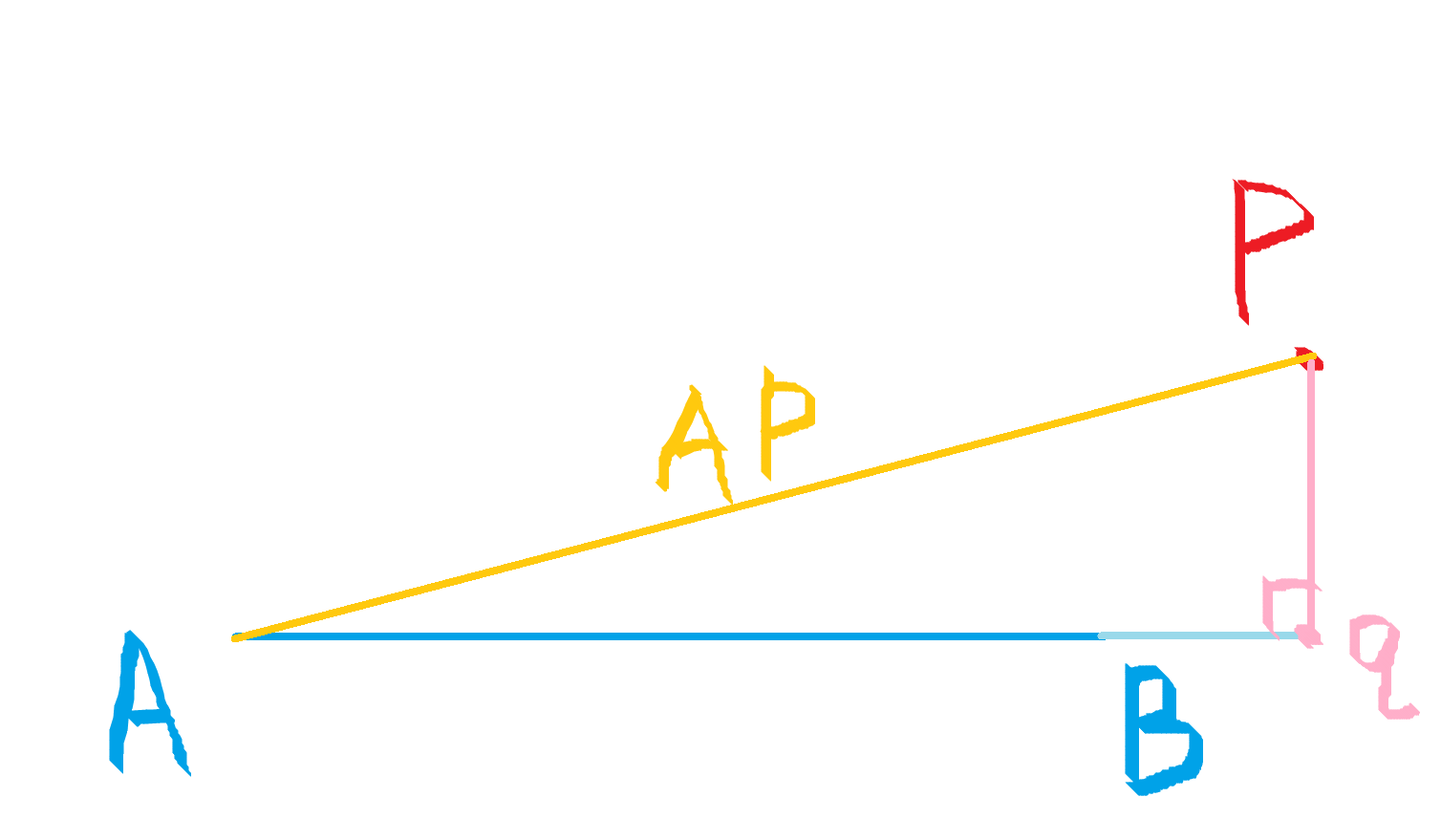
这里的 ,所以
大于 1。
那只要特判比值 是不是大于 1,如果是就直接输出
。
代码:
double calc_len(point p) {return sqrt( p.x * p.x + p.y * p.y );
}// 下面这仨都是重载向量运算符
point operator+(point a, point b) {return {a.x + b.x, a.y + b.y};
}point operator-(point a, point b) {return {a.x - b.x, a.y - b.y};
}double operator*(point a, point b) { //点积 return a.x * b.x + a.y * b.y;
}double calc_dis(point p, line li) {point a = li.a, b = li.b;point ap = p - a, ab = b - a, bp = p - b;double t = ap * ab / (ab.x * ab.x + ab.y * ab.y); // 计算投影比例 t = (ap·ab)/|ab|^2if (t < -eps) { // 投影点在 a 点左侧return calc_len(ap);}if (t - 1 > eps) { // 投影点在 b 点右侧return calc_len(bp);}// 投影点 q 在线段 ab上point pp = {ab.x * t, ab.y * t};point q = a + pp; return calc_len(p - q);
}EX.判断线段与圆是否相交
学了两种方式,我们再来看看前导的第一个例子:

直觉告诉我们,和点到线段的距离有点关系。
实际上,把圆心当作点 P,算出距离 L。
如果 L 小于半径,那么这个线段与圆就相交。
