当前位置：首页 > news >正文

【Algorithm】双指针算法与滑动窗口算法

news 2025/10/5 15:44:39

本篇文章主要讲解双指针算法与滑动窗口算法的概念以及1-2道练习题

1 双指针算法

1）双指针算法的概念

2）移动零

3）快乐数

2 滑动窗口算法

1）滑动窗口算法的概念

2）长度最小的子数组

3 总结

1 双指针算法

1）双指针算法的概念

我们之前在初阶数据结构阶段接触过双指针算法，什么是双指针算法呢？所谓的双指针算法，其实就是利用两个变量在线性结构上遍历。之前我们在数据结构阶段学习过线性结构包括哪些：顺序表、链表以及栈和队列都是线性结构。总之，双指针算法主要是指两个方面：

（1）对于数组或者顺序表，双指针算法是指利用两个整型变量作为下标，使得两个变量相向而行

（2）对于链表，主要是指利用两个指针变量同向而行，也就是我们所熟知的快慢指针

双指针算法可以利用下面的图片来表示：

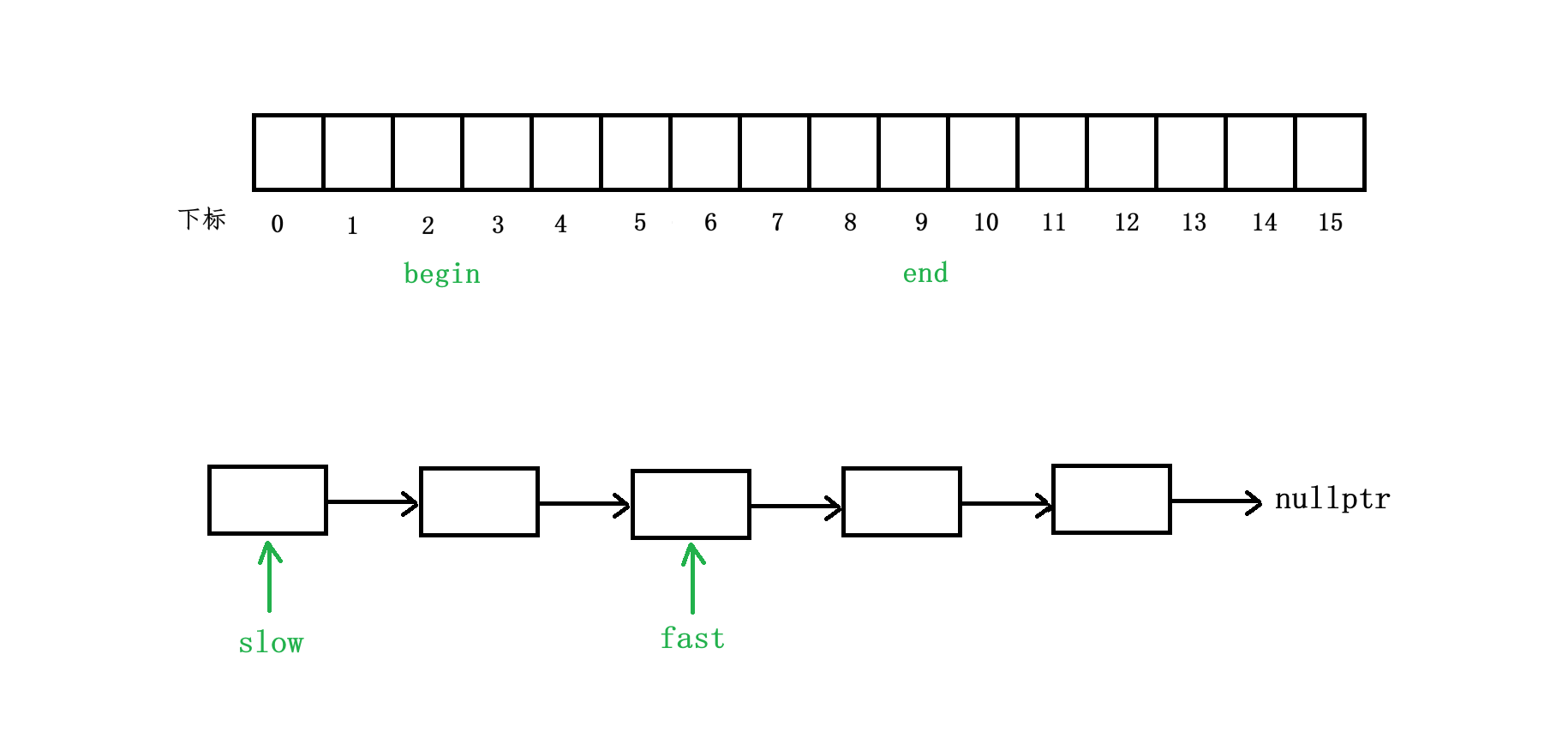
双指针算法呢，本身并不是很难，难的是我们如何确定一个题目可以使用双指针算法，以及如何使用双指针算法解决题目，接下来我们就使用双指针算法来解决具体题目。

2）移动零

leetcode链接：https://leetcode.cn/problems/move-zeroes/?envType=problem-list-v2&envId=two-pointers

题目描述：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:
输入: nums = [0,1,0,3,12]输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]输出: [0]
提示:

1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1

题目解析：

这道题目还是比较好理解的，题目的意思是给你一个数组，里面可能有 0，也可能有其他数字，你需要在原数组上进行操作，将 0 元素全部移到数组的末尾，并且保持之前非 0 元素相对位置不变。比如：数组之前的元素为 0 0 1 2 1 4 7 8 2 0 0，操作完之后，数组中元素应该变为：1 2 1 4 7 8 2 0 0 0 0

算法讲解：

我们可以先来想一下暴力解法，暴力解法我们需要用到两层循环，外层循环我们需要一个 i 整形变量来遍历数组，如果 nums[i] == 0，那么我们就开始内层循环，用一个整形变量 j 从 i + 1 开始遍历数组，如果 nums[j] != 0，那就交换 nums[i] 与 nums[j]，之后跳出循环，这样 i 遍历完数组之后，0 元素就会被交换到数组的末尾，而且由于是从 i 下标元素后面按照非 0 元素出现顺序找 nums[j]，所以非 0 元素的相对位置也是不变的。该算法代码：

class Solution 
{
public:void moveZeroes(vector<int>& nums) {for (int i = 0; i < nums.size(); i++){if (nums[i] == 0){for (int j = i + 1; j < nums.size(); j++){if (nums[j] != 0){swap(nums[i], nums[j]);break;}}}}  }
};

显然，这个算法的时间复杂度为 O(n^2) 的，那么这个代码可不可以进行优化呢？当然是可以优化的，这个算法的核心就是利用一个 i 变量来找 0 元素，利用一个 j 变量来寻找非 0 元素，然后找到之后把他们进行交换，而且 j 变量始终是在 i 变量前面的，所以我们就可以利用双指针算法来对其进行优化，一个来寻找非 0 元素，一个来寻找 0 元素。

双指针算法解决本题的步骤如下：

（1）首先我们创建两个整型变量 prev = -1，cur = 0，我们让 cur 来寻找非 0 元素

（2）当 cur < nums.size() 时，进入循环

（3）如果 nums[cur] != 0，我们先让 prev++，然后交换 nums[cur] 与 nums[prev]

（4）如果 nums[cur] == 0，++cur

可以根据这个算法模拟一下过程，之后根据该算法写出对应代码。

代码：

class Solution 
{
public:void moveZeroes(vector<int>& nums) {int prev = -1, cur = 0;while (cur < nums.size()){// cur 位置不是0，交换cur 与 ++previf (nums[cur] && ++prev != cur)swap(nums[cur], nums[prev]);//其余情况，cur 直接 ++++cur;}    }
};

3）快乐数

leetcode链接：https://leetcode.cn/problems/happy-number/?envType=problem-list-v2&envId=two-pointers

题目描述：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：
输入：n = 19
输出：true
示例 2：
输入：n = 2
输出：false
提示：

1 <= n <= 231 - 1

题目解析：

这个题目的意思就是给你一个数 n，然后让你判断 n 是否是快乐数。快乐数是指将一个数替换为该数字每一位的平方和，然后重复该过程，如果最终可以变为1，那就是快乐数，否则就不是快乐数。题目中有个很关键的点，就是对于一个数字来说，重复这个过程最终可能变到1，也可能无限循环不到1。比如19，1^2 + 9^2 = 82，8^2 + 2^2 = 68，6^2 + 8^2 = 100，1^2 + 0^2 + 0^2 = 1，所以 19 是快乐数。再比如2，2^2 = 4，4^2 = 16，1^2 + 6^2 = 37，3^2 + 7^2 = 58，5^2 + 8^2 = 89，8^2 + 9^2 = 145，1^2 + 4^2 + 5^2 = 42，4^2 + 2^2 = 20，2^2 + 0^2 = 4，到这可以发现，该数字循环了，所以 2 就属于第二种情况，无限循环但是不到 1，所以 2 就不是快乐数。

算法讲解：

这个题目也是一个带环的题，所以由这个题目我们可以联想到之前的判断链表是否有环的问题。之前判断链表是否有环，我们采用快慢指针，slow = slow->next，fast = fast->next->next，之前我们证明过快指针与慢指针一定会在环中相遇。那么类比与那个题目，既然快乐数只有两种情况，一种是最终一定会到1，另一种是会无限循环但是到不了1，其实一定到1也是一种循环，只不过循环中的所有数字都是1罢了，那么我们也可以用快慢指针，让 slow 一次走一步，fast 一次走两步，他们一定会相遇，如果相遇时值是 1，那就说明其是快乐数，如果不是1，那就不是快乐数。需要注意的是，这里的 slow 与 fast 不是指针，而是整形变量。

代码：

class Solution 
{
public:bool isHappy(int n) {//使用快慢指针int slow = BitSum(n), fast = BitSum(BitSum(n));while (slow != fast){slow = BitSum(slow);fast = BitSum(BitSum(fast));}return fast == 1;}int BitSum(int num){int ret = 0;while (num){ret += (num % 10) * (num % 10);num /= 10;}return ret;}
};

2 滑动窗口算法

1）滑动窗口算法的概念

滑动窗口算法也属于双指针算法，只不过其指的是双指针在数组上同向移动的算法（一般两个指针都是从左向右移动），所以也可以形象的称为“同向双指针算法”。双指针算法可以用下面的一张图形象的进行表示：

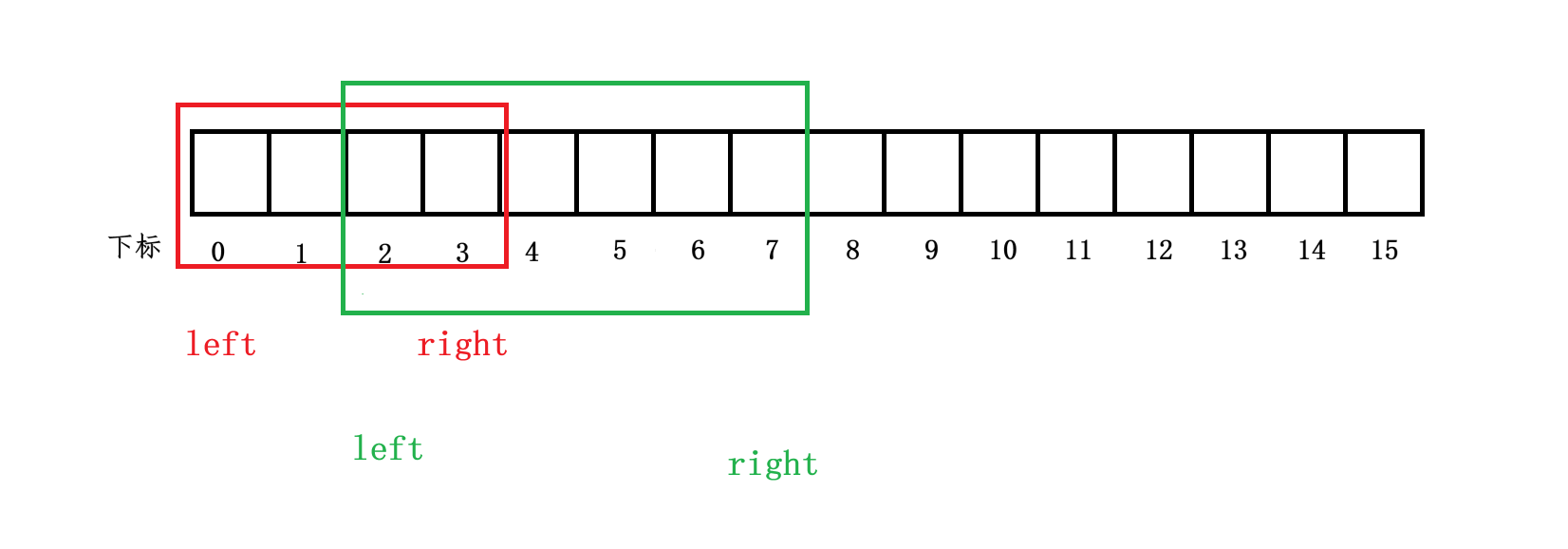
由于这个算法很像一个窗口在数组上进行滑动，所以被形象的称为滑动窗口算法。

那么什么时候采用滑动窗口算法呢？当我们发现两个指针能够同向移动解决问题的时候，我们就可以采用滑动窗口算法。使用滑动窗口解决问题的步骤主要分为四步：

（1） 定义两个整型变量 left = 0，right= 0，让 left 作为窗口的左端点，right 作为窗口的右端点

（2） 进窗口

（3）判断，然后在循环里是否要出窗口

（4）选择一个合适的地方更新结果

这样讲解比较抽象，我们根据一道具体的题目来说明。

2）长度最小的子数组

leetcode链接：https://leetcode.cn/problems/2VG8Kg/description/?envType=problem-list-v2&envId=sliding-window

题目描述：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4]
输出：1
示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0
提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

题目解析：

这道题目就是给你一个数组，里面的数字全部都是正整数，然后给你一个整数值 target，当一个子数组的元素的和 >= target 时，那这就是一个满足要求的子数组，然后题目是让你求出长度最小的子数组的长度。注意：子数组是指数组中一段连续的区间，不能断开。

算法讲解：

我们先来看一下这道题目的暴力解法，暴力解法很简单，就是找到题目中所有的子数组，然后求和，判断该子数组的和是否 >= target，如果满足，那就记录一下，最后求出所有满足条件的子数组的最小值就可以了。暴力解法的代码：

class Solution 
{
public:int minSubArrayLen(int target, vector<int>& nums) {int len = INT_MAX;//i来作为子数组的左端点for (int i = 0; i < nums.size(); i++){//j作为子数组的右端点for (int j = i; j < nums.size(); ++j){if (Sum(nums, i, j) >= target)len = min(len, j - i + 1);}}return len == INT_MAX ? 0 : len;}int Sum(vector<int>& nums, int begin, int end){int sum = 0;for (int i = begin; i <= end; ++i)sum += nums[i];return sum;}
};

分析一下暴力解法的时间复杂度，首先外面有两层循环，复杂度为 O(n^2)，然后求和的时候又会遍历一遍数组，所以暴力解法时间复杂度为 O(n^3) 的。可以看到时间复杂度是很高的，所以直接提交的话是会超出时间限制的。

我们可以在暴力解法的基础上进行优化，暴力解法的时间复杂度高就是因为其枚举了很多不必要的情况，比如以下这个数组：

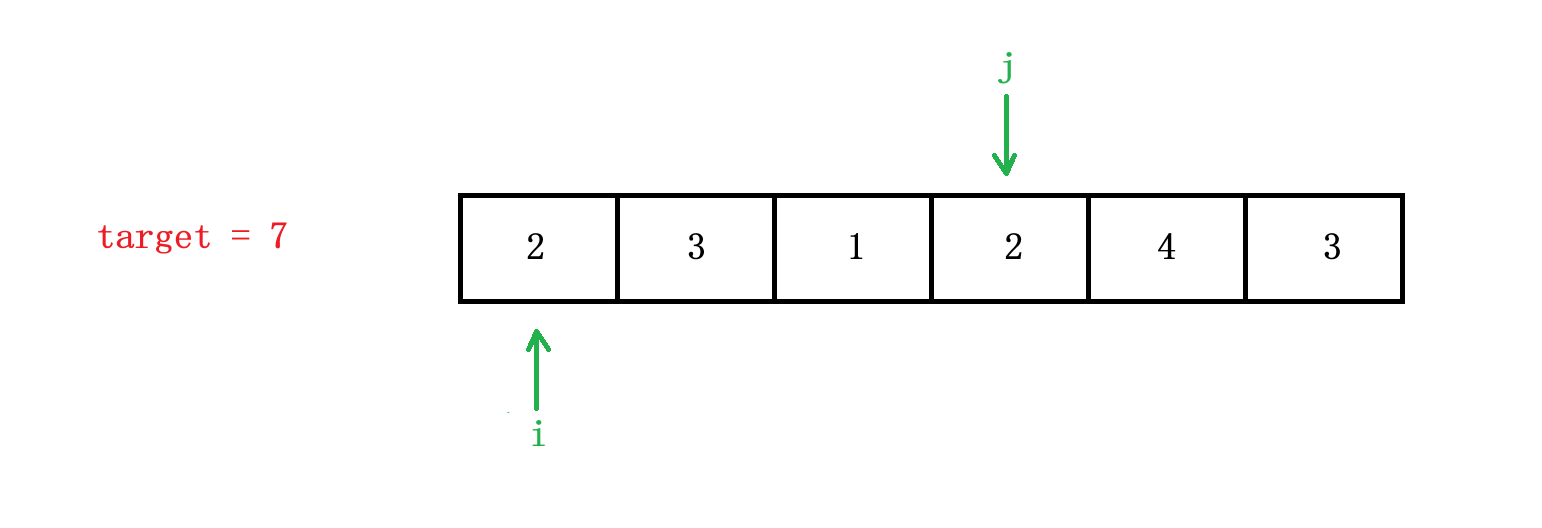
当遍历到这种情况的时候，sum 此时已经 > target 了，并且由于求得是最短子数组的长度，而且数组中都是正整数，所以 j 再往后走 sum += nums[j] 后，都会 > target，但是子数组的长度一定会比此时长，所以这种情况就是 i = 0 时，满足条件的最短子数组，j 无需再向后遍历。

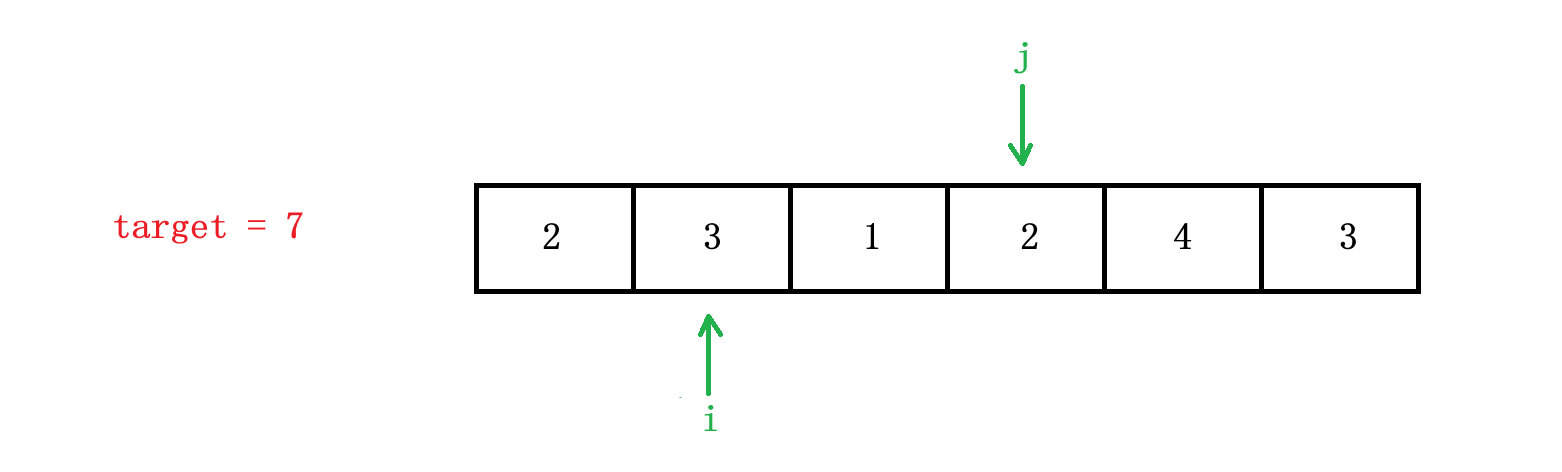
当 i = 1 时，暴力解法中需要 j 从 i 这个位置开始遍历，求 sum，但是其实 sum 可以由上一种情况直接求得，直接用 sum -= nums[i] 就可以求出 sum 了，所以 j 是无需向后走的，分析到这我们可以发现其实 i 和 j 是同向移动的，所以我们可以采用滑动窗口算法来解决这个问题。

滑动窗口算法解决该问题，就用上面四步，第一步先定义 left = 0，right = 0，还需要一个 sum 变量来记录元素的和，还有一个 len 变量来记录子数组的长度，由于求的是最小长度，所以我们将 len 初始化为 INT_MAX。那么进窗口很简单，就是 sum += nums[right]，判断条件就是当 sum >= target 时，此时出窗口，也就是 sum -= nums[left]，++left；由于我们求得是满足条件的最短长度，也就是当 sum >= target 时，长度就是我们所求，所以我们在出窗口之前就需要更新结果，即 len = min(len, right - left + 1)。

代码：

class Solution 
{
public:int minSubArrayLen(int target, vector<int>& nums) {int len = INT_MAX;int left = 0, right = 0;int sum = 0;while (right < nums.size()){//进窗口sum += nums[right];//判断while (sum >= target){//更新结果len = min(len, right - left + 1);//出窗口sum -= nums[left];++left;}++right;}return len == INT_MAX ? 0 : len;}
};

由于只遍历了一遍数组，所以时间复杂度是 O(n) 的。