【LLM-RL】GRPO->DAPO->GSPO训练区别
note
- GRPO的创新与局限:GRPO简化了PPO,主要变化
- ✅ 用规则函数替代奖励模型
- ✅ 取消了价值模型
- ✅ 优势函数改为输出序列奖励值的标准化
- 但GRPO存在三大问题:
- 序列级奖励与token级动作粒度不匹配
- 重要性采样方差偏移累积
- MOE模型上训练不稳定
- DAPO的四大改进
- 移除KL散度约束
- 非对称裁剪(Clip-Higher)
- 动态采样策略
- token级别的梯度计算
- GSPO的核心思想:针对MOE模型的特殊性,GSPO将动作粒度提升到序列级别
- 使用序列重要性采样的几何平均
- 减少单个token方差影响
- 更适合专家路由机制
文章目录
- note
- 一、GRPO->DAPO->GSPO算法
- 1、PPO和DPO算法回顾
- 2、快速看GRPO->DAPO->GSPO训练区别
- 🚩 GRPO的创新与局限
- ✨ DAPO的四大改进
- 💡 GSPO的核心思想
- 二、GRPO->DAPO->GSPO算法对比
- 1. GRPO (Group Relative Policy Optimization)
- 记号统一与组相对优势(组内标准化)
- GRPO 算法核心
- 2. DAPO (Decoupled clip & Dynamic sampling Policy Optimization)
- 3. GSPO (Group Sequence Policy Optimization, Qwen)
- 三、实践建议
- Reference
一、GRPO->DAPO->GSPO算法
1、PPO和DPO算法回顾
PPO在LLM中的应用主要是调节模型输出,使其更符合人类偏好。关键组件包括:
1️⃣ 奖励模型(RM)
2️⃣ 价值模型(Value)
3️⃣ Actor模型(主模型)
4️⃣ 参考模型
PPO训练目标函数公式见上图,其中优势函数计算有TD、MC、GAE三种主要方式。

- 上图简介:策略模型根据input得到response,然后奖励模型对response进行打分;然后critic model会预测response的未来累计奖励,计算GAE函数;critic model的结果就能帮助策略模型的优化。注意GAE的输入有critic model和reward model的结果。
- 在RLHF中(比如MOSS-RLHF)是使用奖励模型来初始化评论家模型(critic model)和奖励模型(reward model),评论家模型也使用奖励模型初始化,便于在早期提供较准确的状态值估计;但是注意PPO会对策略模型、评论家模型训练并更新;奖励模型、参考模型不参与训练。
- 异策略:固定一个演员和环境交互(不需要更新),将交互得到的轨迹交给另一个负责学习的演员训练。PPO就是策略梯度的异策略版本。通过重要性采样(这里使用KL散度)进行策略梯度的更新。PPO解决了传统策略梯度方法的缺点:高方差、低数据效率、易发散等问题。
- PPO-clip算法通过引入裁剪机制来限制策略更新的幅度,使得策略更新更加稳定
- DPO更新参数,目标函数:LDPO(πθ;πref)=−E(x,yw,yl)∼D[logσ(βlogπθ(yw∣x)πref(yw∣x)−βlogπθ(yl∣x)πref(yl∣x))]\mathcal{L}_{\mathrm{DPO}}\left(\pi_\theta ; \pi_{\mathrm{ref}}\right)=-\mathbb{E}_{\left(x, y_w, y_l\right) \sim \mathcal{D}}\left[\log \sigma\left(\beta \log \frac{\pi_\theta\left(y_w \mid x\right)}{\pi_{\mathrm{ref}}\left(y_w \mid x\right)}-\beta \log \frac{\pi_\theta\left(y_l \mid x\right)}{\pi_{\mathrm{ref}}\left(y_l \mid x\right)}\right)\right] LDPO(πθ;πref)=−E(x,yw,yl)∼D[logσ(βlogπref(yw∣x)πθ(yw∣x)−βlogπref(yl∣x)πθ(yl∣x))]
- 注意:奖励函数rrr和策略πππ的关系推倒出来后,就能把ranking loss中的奖励函数rrr替换
- 目标函数含义:如果是好答案,则尽可能增大被policy策略模型生成的概率
- DPO实际在最大化偏好概率的对数似然,从而使得模型更倾向于生成符合人类偏好的响应。
2、快速看GRPO->DAPO->GSPO训练区别
🚩 GRPO的创新与局限
GRPO简化了PPO,主要变化:
✅ 用规则函数替代奖励模型
✅ 取消了价值模型
✅ 优势函数改为输出序列奖励值的标准化
但存在三大问题:
- 序列级奖励与token级动作粒度不匹配
- 重要性采样方差偏移累积
- MOE模型上训练不稳定
✨ DAPO的四大改进
1️⃣ 移除KL散度约束
2️⃣ 非对称裁剪(Clip-Higher)
3️⃣ 动态采样策略
4️⃣ token级别的梯度计算
💡 GSPO的核心思想
针对MOE模型的特殊性,GSPO将动作粒度提升到序列级别:
- 使用序列重要性采样的几何平均
- 减少单个token方差影响
- 更适合专家路由机制
二、GRPO->DAPO->GSPO算法对比
1. GRPO (Group Relative Policy Optimization)
记号统一与组相对优势(组内标准化)
对同一提示 xxx 从旧策略 πθold\pi_{\theta_{old}}πθold 生成 GGG 个完整回应 {yi}i=1G\{y_{i}\}_{i=1}^{G}{yi}i=1G。第 iii 条回应长度为 ∣yi∣|y_{i}|∣yi∣,其第 ttt 个 token 为 yi,ty_{i,t}yi,t。对每条回应用奖励函数得到标量奖励 r(x,yi)r(x,y_{i})r(x,yi)。
常见的组相对优势(组内标准化)写作:
A^i=r(x,yi)−meanjr(x,yj)stdjr(x,yj).\hat{A}_{i}=\frac{r(x,y_{i})-\text{mean}_{j}r(x,y_{j})}{\text{std}_{j}r(x,y_{j})}. A^i=stdjr(x,yj)r(x,yi)−meanjr(x,yj).
多数实现将同一回应内所有 token 共享同一优势,即 A^i,t=A^i\hat{A}_{i,t}=\hat{A}_{i}A^i,t=A^i。此设定见 DeepSeek/GRPO 与 Qwen/GSPO 的论文与实现说明。
GRPO 算法核心
核心思想:不用价值网络,直接在组内做相对比较得到优势;优化仍采用 PPO 的比率+截断框架,但在 token 级进行比率与裁剪。
目标(最大化):
JGRPO(θ)=E[1G∑i=1G1∣yi∣∑t=1∣yi∣min(ri,t(θ)A^i,clip(ri,t(θ),1−ε,1+ε)A^i)]−βDKL(πθ∣πref),J_{\text{GRPO}}(\theta)=\mathbb{E}\left[\frac{1}{G} \sum_{i=1}^{G} \frac{1}{|y_{i}|} \sum_{t=1}^{|y_{i}|} \min \left( r_{i, t}(\theta) \hat{A}_{i}, \operatorname{clip}\left( r_{i, t}(\theta), 1-\varepsilon, 1+\varepsilon\right) \hat{A}_{i}\right)\right]-\beta D_{\mathrm{KL}}\left(\pi_{\theta}\vert\pi_{\text{ref}}\right), JGRPO(θ)=EG1i=1∑G∣yi∣1t=1∑∣yi∣min(ri,t(θ)A^i,clip(ri,t(θ),1−ε,1+ε)A^i)−βDKL(πθ∣πref),
其中
ri,t(θ)=πθ(yi,t∣x,yi,<t)πθold (yi,t∣x,yi,<t).r_{i, t}(\theta)=\frac{\pi_{\theta}\left(y_{i, t} \mid x, y_{i,< t}\right)}{\pi_{\theta_{\text{old }}}\left(y_{i, t} \mid x, y_{i,< t}\right)}. ri,t(θ)=πθold (yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t).
2. DAPO (Decoupled clip & Dynamic sampling Policy Optimization)
核心思想:在长 CoT 的大规模 RL 实践中,DAPO 指出样本级 汇总会让长答案的惩罚不足、训练不稳;因此采用 token 级归并的目标、非对称裁剪区间(εlow\varepsilon_{\text{low}}εlow,εhigh\varepsilon_{\text{high}}εhigh),并配合动态采样/过滤(剔除极端样本以保持有效梯度)、超长样本的特殊处理等工程策略,显著提升稳定性与可复现性。
目标(token 级、非对称裁剪,最大化):
JDAPO(θ)=E[1∑i∣yi∣∑i=1G∑t=1∣yi∣mini(ri,t(θ)A^i,clip(ri,t(θ),1−εlow,1+εhigh)A^i)],J_{\text{DAPO}}(\theta)=\mathbb{E}\left[\frac{1}{\sum_{i}|y_{i}|}\sum_{i=1}^{G}\sum_{t=1}^{|y_{i}|}\min_{i}\left(r_{i,t}(\theta)\hat{A}_{i},\text{clip}(r_{i,t}(\theta),1-\varepsilon_{\text{low}},1+\varepsilon_{\text{high}})\hat{A}_{i}\right)\right], JDAPO(θ)=E∑i∣yi∣1i=1∑Gt=1∑∣yi∣imin(ri,t(θ)A^i,clip(ri,t(θ),1−εlow,1+εhigh)A^i),
其中 ri,t(θ)r_{i,t}(\theta)ri,t(θ) 同 GRPO;论文同时详细描述了动态采样与超长截断样本的处理/惩罚等做法。
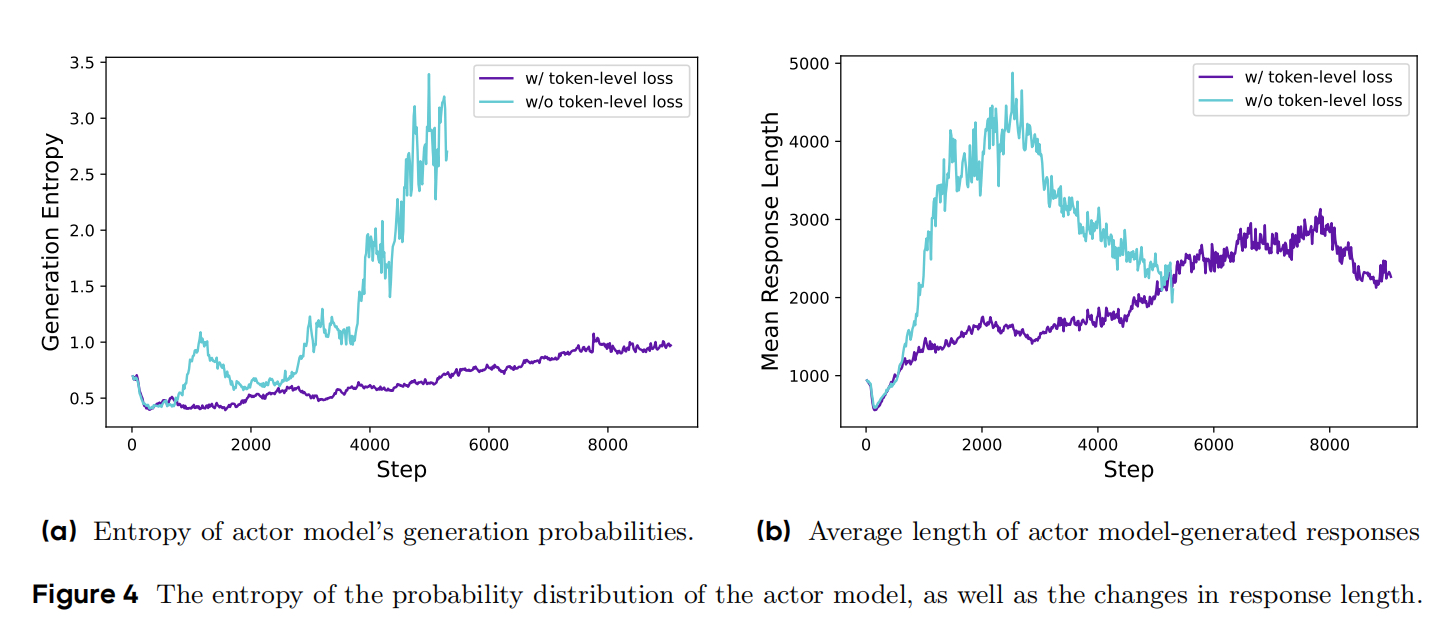
实验证明,DAPO在长思维链任务中表现更稳定,收敛更快(见对比曲线图)。
3. GSPO (Group Sequence Policy Optimization, Qwen)
核心思想:GRPO 在 token 级做重要性比率,但奖励是序列级,两者不匹配会带来不稳;GSPO 把重要性比率与裁剪提升到"序列级",让优化单元与奖励单元一致,稳定性与样本效率更好,特别适用于大规模/MoE 训练。
目标(序列级裁剪,最大化):
JGSPO(θ)=E[1G∑i=1Gmin(si(θ)A^i,clip(si(θ),1−ε,1+ε)A^i)],J_{\text{GSPO}}(\theta)=\mathbb{E}\left[\frac{1}{G} \sum_{i=1}^{G} \min \left(s_{i}(\theta) \hat{A}_{i}, \operatorname{clip}\left(s_{i}(\theta), 1-\varepsilon, 1+\varepsilon\right) \hat{A}_{i}\right)\right], JGSPO(θ)=E[G1i=1∑Gmin(si(θ)A^i,clip(si(θ),1−ε,1+ε)A^i)],
其中序列级重要性比率常写成长度归一的形式:
si(θ)=(πθ(yi∣x)πθold (yi∣x))1/∣yi∣=exp(1∣yi∣∑t=1∣yi∣logπθ(yi,t∣x,yi,<t)πθold (yi,t∣x,yi,<t)).s_{i}(\theta)=\left(\frac{\pi_{\theta}\left(y_{i} \mid x\right)}{\pi_{\theta_{\text{old }}}\left(y_{i} \mid x\right)}\right)^{1 /|y_{i}|}=\exp \left(\frac{1}{|y_{i}|} \sum_{t=1}^{|y_{i}|} \log \frac{\pi_{\theta}\left(y_{i, t} \mid x, y_{i, < t}\right)}{\pi_{\theta_{\text{old }}}\left(y_{i, t} \mid x, y_{i,<t}\right)}\right). si(θ)=(πθold (yi∣x)πθ(yi∣x))1/∣yi∣=exp∣yi∣1t=1∑∣yi∣logπθold (yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t).
(论文与官方博客均强调"序列级比率+序列级裁剪"。)
三、实践建议
算法对比:
- GRPO:组相对优势+token 级比率与裁剪;实现简单、无需价值函数,但在长序列/大模型时可能不稳。
- DAPO:工程向增强:token 级归并+非对称裁剪+动态采样+超长样本处理,用于长 CoT 的大规模可复现 RL。
- GSPO:把比率/裁剪移到序列级,与序列级奖励匹配,报告在稳定性与效率上优于 GRPO,MoE 训练尤甚。
方法选择:
- 简单任务:GRPO足够高效
- 长文本任务:优先考虑DAPO
- MOE架构:必须使用GSPO
- 超参设置:组规模N需足够大
Reference
[1] DAPO: An Open-Source LLM Reinforcement Learning System at Scale
