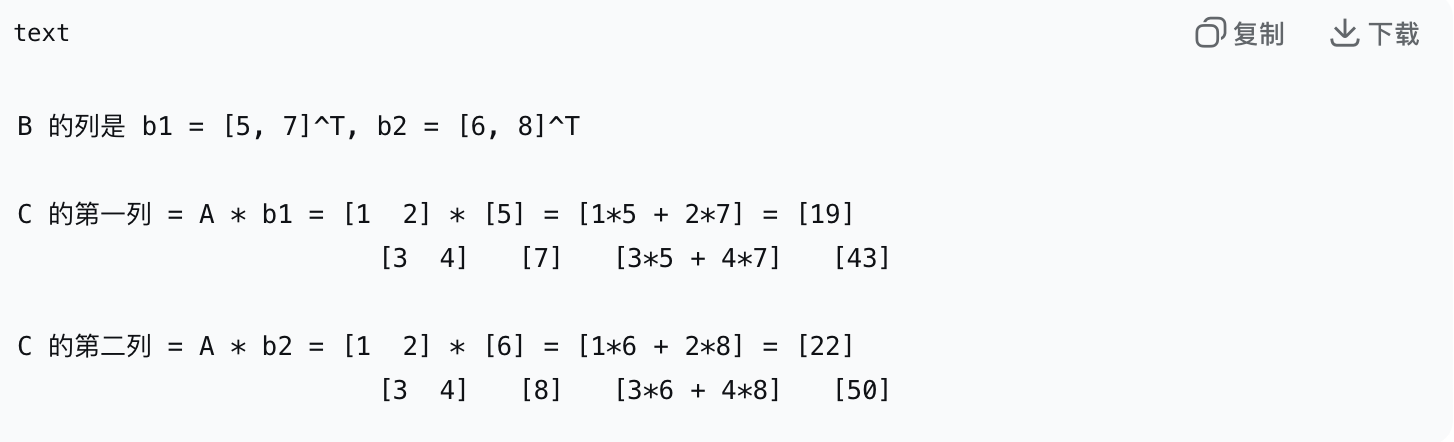1.矩阵的乘法
2.矩阵乘法的性质
1.矩阵的乘法
1).元素视角(点乘)a.核心思想: 结果矩阵C的第i行第j列的元素c_ij, 等于左矩阵A的第i行向量与右矩阵B的第j列向量的点积b.计算过程- 找到A的第i行: (a_i1, a_i2, ..., a_ip)- 找到B的第j列: (b_1j, b_2j, ..., b_pj)- 计算它们的点积: c_ij = a_i1 * b_1j + a_i2 * b_2j + ... + a_ip * b_pjc.要求: A的列数必须等于B的行数(假设A是m * p, B是p * n, 结果C是m * n)

2).列视角(矩阵 * 列向量)将右矩阵B看作是由多个列向量组合而成a.核心思想: 结果矩阵C的每一列, 是左矩阵A与B的对应列向量的线性组合b.计算过程:设B = [b1, b2, ..., bn], 其中b_j是B的第j列那么C = A * B = [A*b1, A*b2, ..., A*bn]
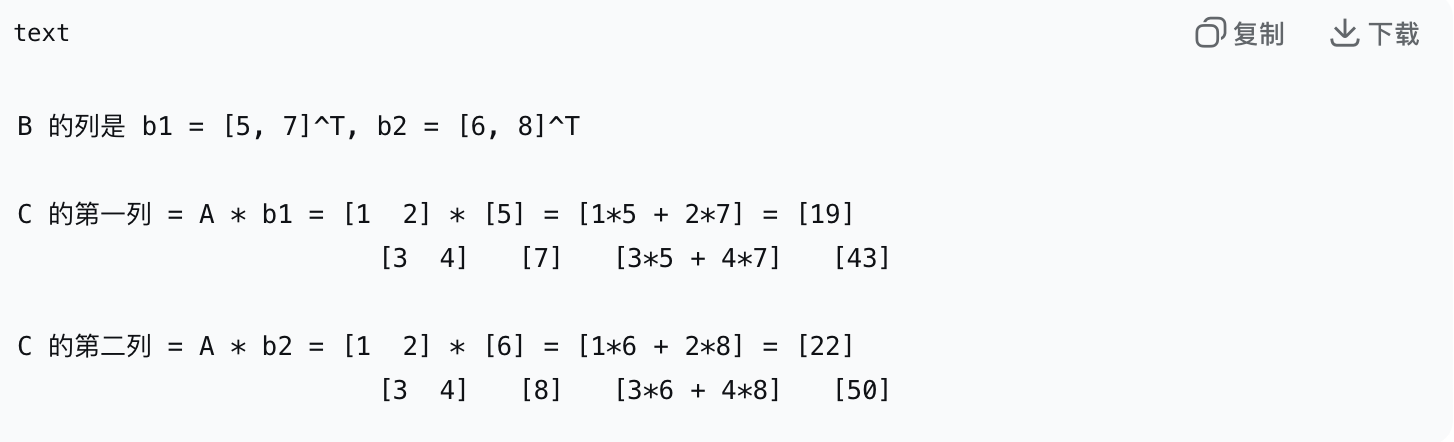
3).行视角(行向量 * 矩阵)将左矩阵A看作是由多个行向量组合而成a.核心思想: 结果矩阵C的每一行, 是右矩阵B与A的对应行向量的线性组合b.计算过程:设A = [a1; a2; ...; am]^T, 其中a_i是A的第i行(行向量)那么C = A * B, 其第i行c_i等于a_i * B

4).列行展开, 以2 * 2的矩阵举例

a.分解矩阵

b.计算各个外积(外积是两个向量相乘得到矩阵)

c.求和得到最终结果

2.矩阵乘法的性质
a.矩阵乘法的结合律A * (B * C) = (A * B) * Cb.矩阵乘法的分配律A * (B + C) = (A * B) + (A * C)