前向传播与反向传播(附视频链接)

b站视频链接

一、前向传播（Forward Propagation）

1. 基本概念

前向传播是神经网络从输入数据出发，通过逐层计算（线性变换 + 激活函数），最终得到预测输出并计算损失值的过程。

核心作用：将输入 “映射” 为输出，同时生成损失函数（衡量预测与真实标签的差距），为反向传播提供 “优化目标”。

适用场景：所有参数化模型（如线性回归、全连接神经网络、CNN、Transformer 等），本质是 “参数→输出→损失” 的正向计算链。

2. 核心流程

本文举例的神经网络为：隐藏层为h，有2个神经单元，1表示偏置，

下图为y₂的计算过程，非线性变换采用sigmod激活函数

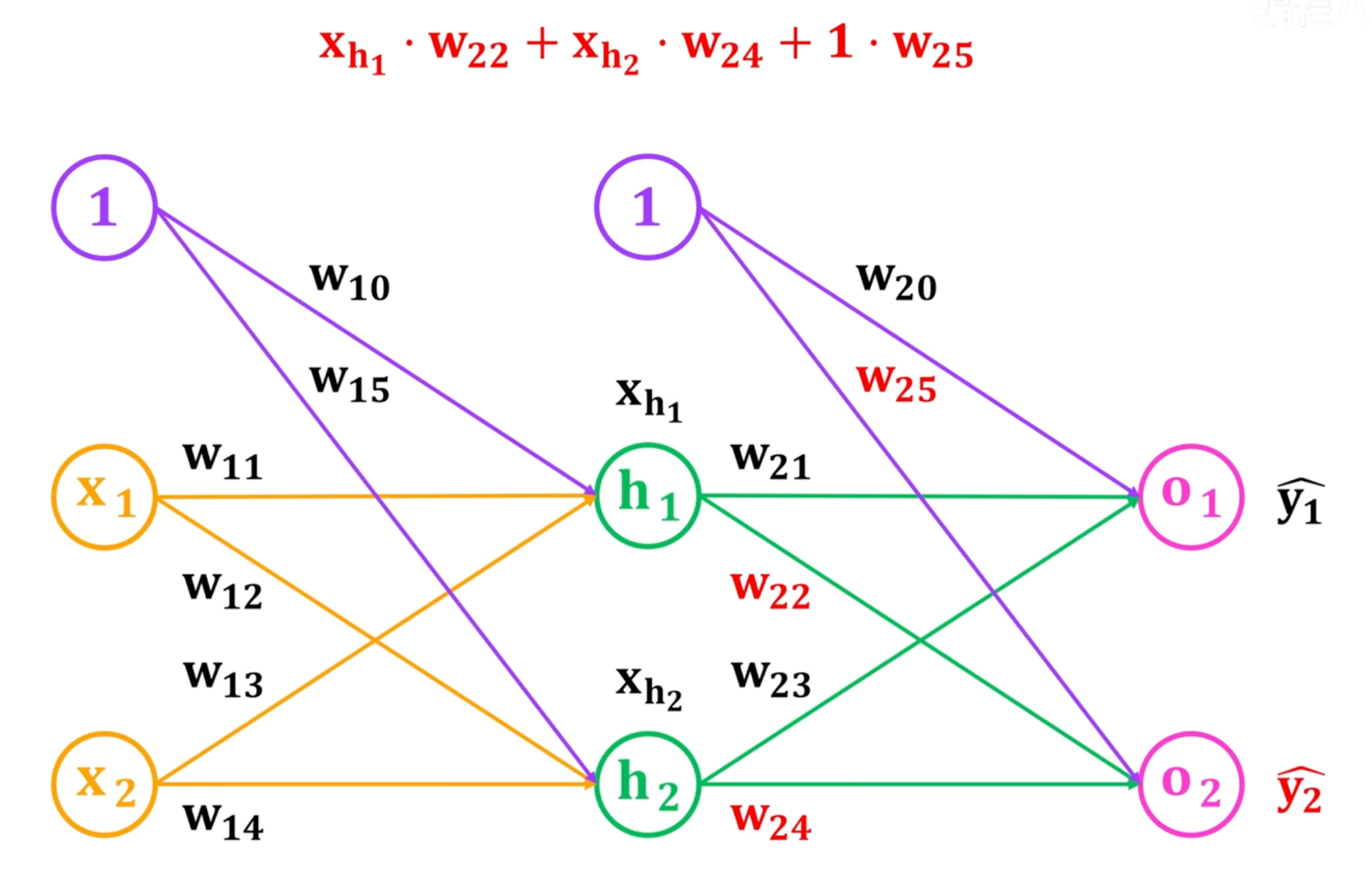
计算示例

二、反向传播（Backward Propagation）

1. 基本概念

反向传播是从损失值出发，通过 “链式法则” 反向计算每个参数（W，b）对损失的梯度（即$\frac{\partial \mathcal{L}}{\partial W},\frac{\partial \mathcal{L}}{\partial b}$）的过程。

核心作用：为梯度下降提供 “参数更新的方向和幅度”—— 梯度表示 “参数变化 1 单位时，损失的变化量”，是优化参数的核心依据。

本质：将 “全局损失” 分解为 “每个局部参数的梯度”，避免暴力计算，大幅降低计算量。

2. 核心流程

总损失：

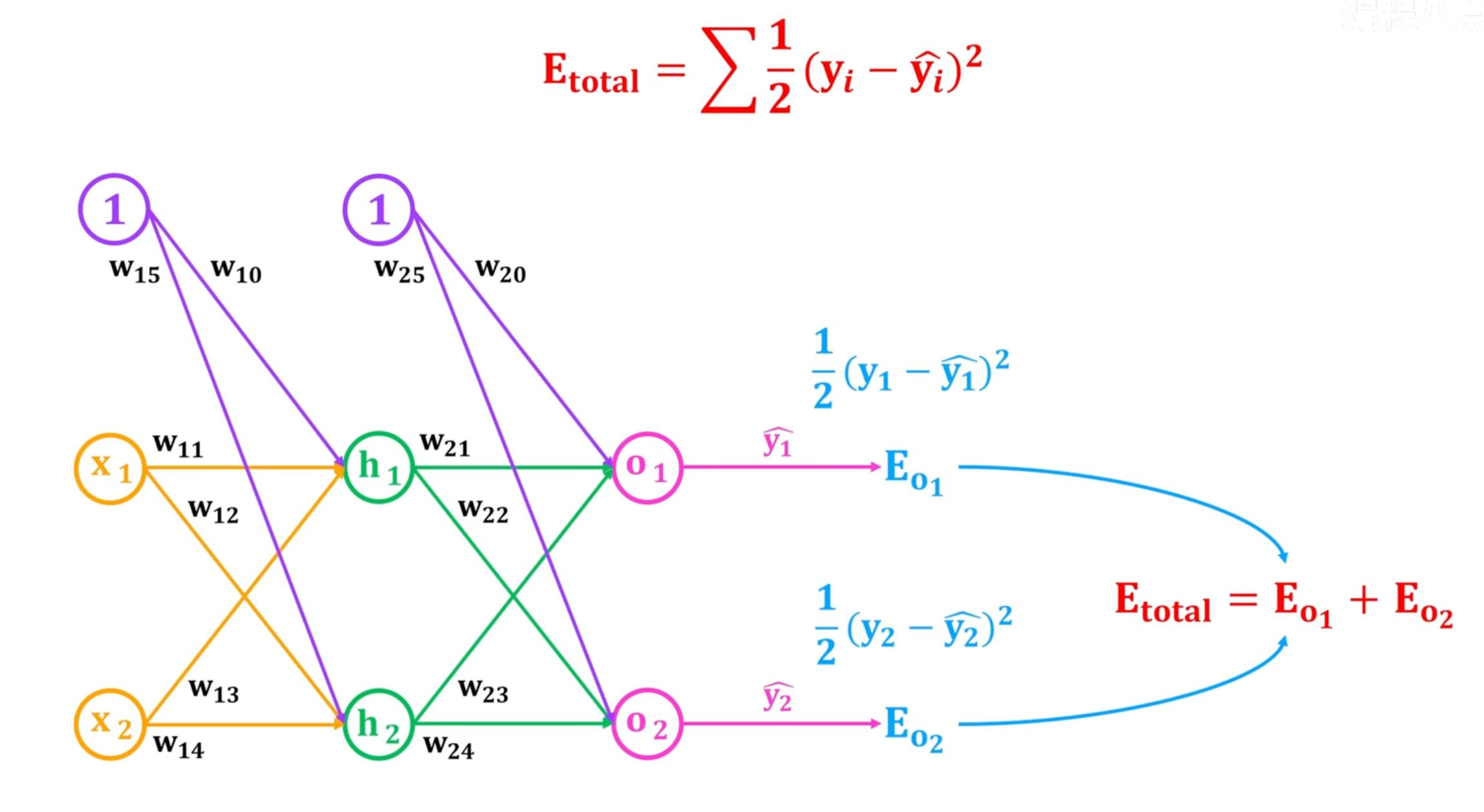
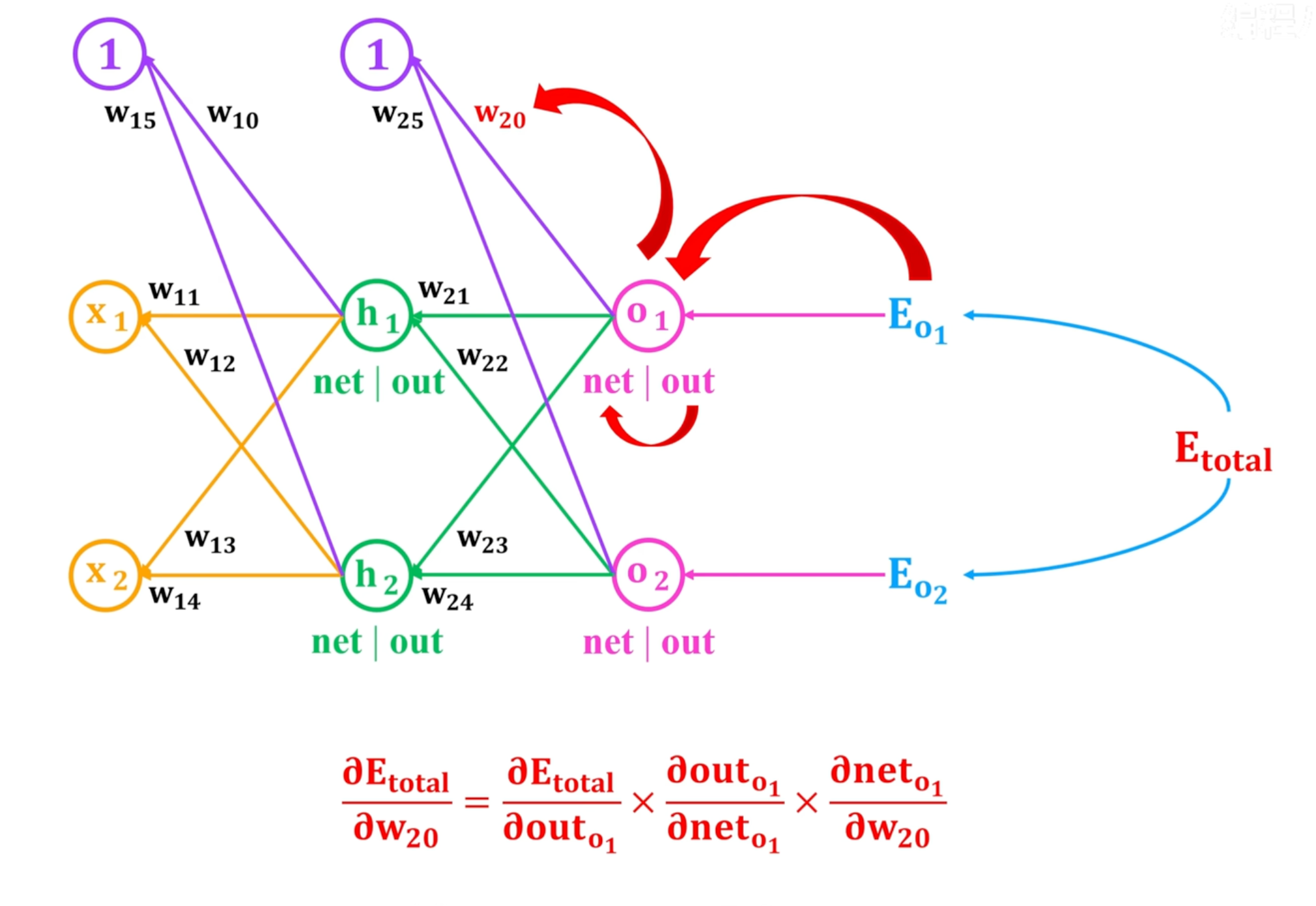
w₂₀的梯度计算流程，本质是链式法则求偏导

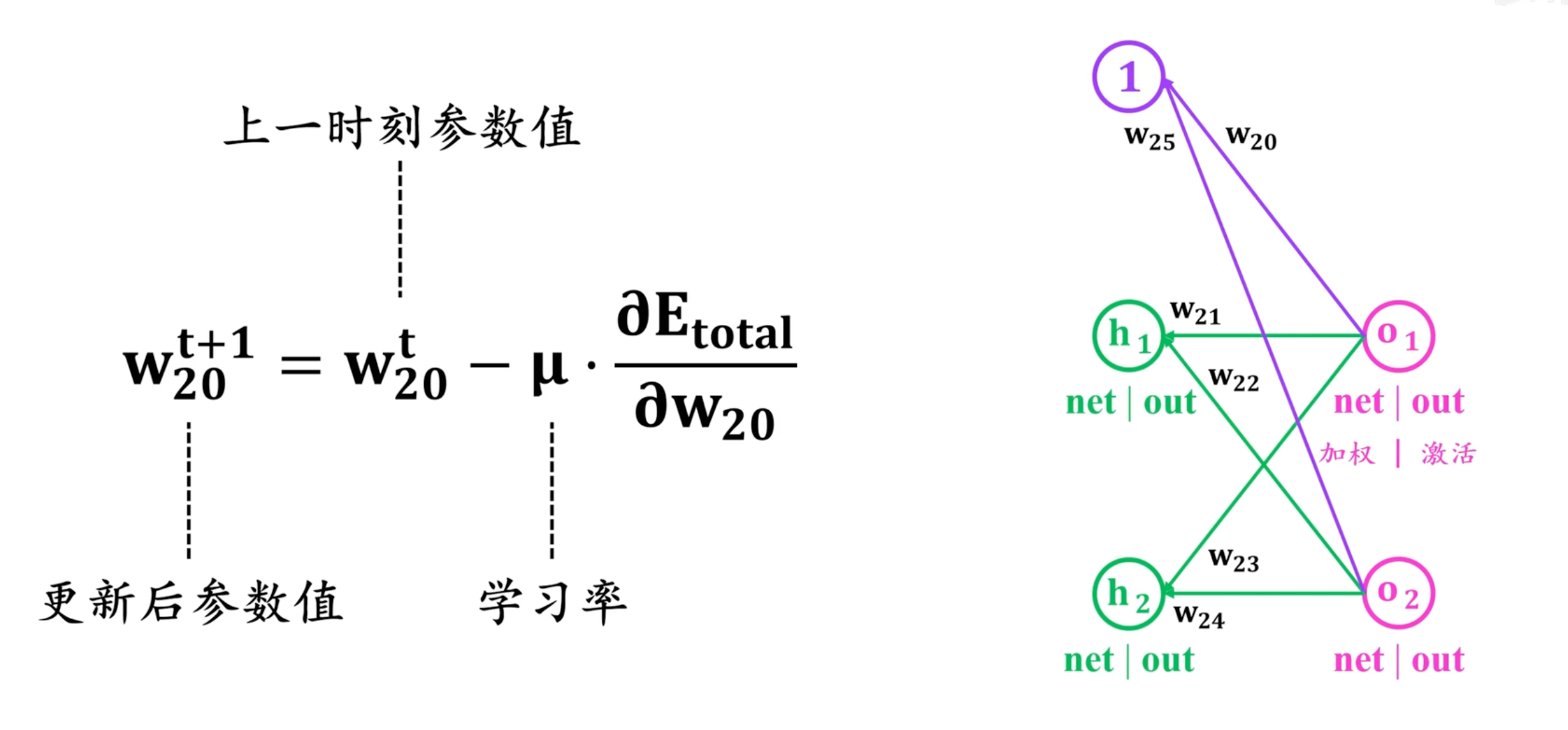
更新w₂₀参数，利用梯度下降法。同理可更新其他参数，注意如w₁₁这层的参数更新需要考虑到E_o1和E_o2的反向传递

三、前向传播与反向传播的联系

维度	前向传播（Forward）	反向传播（Backward）+ 梯度下降
计算方向	输入→隐藏层→输出（正向）	损失→输出层→隐藏层→输入层（反向）
核心目的	计算预测值$\hat{y}$和损失 $\mathcal{L}$	计算参数梯度$\frac{\partial \mathcal{L}}{\partial \theta }$，更新参数减小损失
核心操作	线性变换（$z=xW+b$）+ 激活函数	链式法则（梯度传递）+ 梯度下降（参数更新）
依赖关系	依赖输入数据和当前参数	依赖前向传播的中间结果（$z_1,h_1,z_2$）和损失

四、总结

1. 前向传播是 “基础”：没有前向传播的损失值，反向传播就没有优化目标；
2. 反向传播是 “关键”：没有反向传播的梯度，梯度下降就无法确定参数更新方向；
3. 三者构成训练循环：前向传播→计算损失→反向传播求梯度→梯度下降更新参数→重复迭代，直到损失收敛到最小值。
4. 通用性：无论网络结构多复杂（如 CNN 的卷积层、Transformer 的注意力层），前向 / 反向传播的核心逻辑不变 —— 只是线性变换和激活函数的形式不同，梯度计算的细节需适配结构调整。