动力学系统辨识与建模
考试结束好久了,刚刚才发现在草稿箱里。都是复习时候的总结,发出来希望对学习课程的同学有所帮助,虽然看起来难,其实考的挺简单的
一、系统辨识
1.1 是什么?
利用系统的输入输出信息进行建模,是一种实验(数据)建模的方法
①什么是系统?
系统是由内部相互联系、相互制约、相互作用的要素构成,受外部要素制约,具有整体功能和综合行为的统一体,系统的模型就是建立在表征系统状态参数之间以及外作用之间的相互作用的数学表达式
②什么是实验建模?
白箱问题,常使用机理建模(第一建模原理),不需用数据,通过分析过程的运动规律,运用严格的演绎推理和计算机仿真求解得到系统的模型,其一般来说建模过程都很复杂;无法排除实际或者长期运行出现的干扰;后续的验证与测试耗时
黑箱问题,其内部物理特性未知,无法采用机理建模、理论建模精度较低或者需要考虑实际情况的损失 ,使用实验建模(系统辨识),通过对系统持续施加激励信号获取外部输出信息,并在此基础上采用统计学估计,应用系统辨识的方法建立系统模型
灰箱问题,机理与实验相结合建模,满足部分规律,但部分机理仍不明晰,结合使用两种方法
全面描述系统的模型是很难得到的,可以建立多个不同的模型描述系统,每个模型仅在一定情况下成立
1.2 产生和发展
古代,大都凭借经验;现代得益于数学的发展,之后现代控制理论及计算机控制技术的应用,诞生了在线辨识(数据处理方法可以在线实现);最后由于超算、人工智能的实现,使结果更加智能
| 1962 L.A.Zadel | 辨识就是在输入输出数据的基础上,从一组给定的模型中,确定一个与所测系统等价的模型 明确三大要素:数据、模型类、等价准则 数据是辨识的基础、准则是辨识的依据、模型类是辨识的范围 | 此定义寻找模型较为困难,不实用 |
| 1974 P.Eykhoff | 可归结为用一个模型来表示客观系统本质特征的演算,并用这个模型把对客观系统的理解表示为有用的形式 | 最终模型只应表示动态系统的本质,并且把它表示成适当的形式。这也就意味着不是期望获得一个实际的确切的数学描述,只是需要一个实用的应用模型 |
| 1978 L.Ljung | 辨识有三个要素:数据、模型类和准则。辨识就是按照一个准则在一组模型类中寻找一个与数据拟合得最好的模型 | 由于观测到的数据一般包含系统运行过程噪声和仪器测量噪声,因此通过辨识进行建模不过是实际过程特性的一种近似描述。这一定义较好地反映了辨识方法的数理统计本质,被从事这一领域研究和应用的科研工作者广泛采用 |
| 1994 蔡金狮《飞行器系统辨识》 | 系统辨识是一门通过观测系统试验过程中输入 — 输出关系来建立系统数学模型的技术学科,也是一门基于现代控制理论发展起来已开拓到自然科学、社会科学和应用技术科学众多领域的交叉学科 | 明确系统辨识是一门技术学科,同时反映了它的发展趋势 |
1.3 重要概念
①模型集:常取为最简单的线性代数形式,之后推广为多项式形式;现在开始采用样条函数、指数函数、超越函数,甚至有限元、有限体积元、神经网络元作为候选数学模型集。
②辨识准则:最早的辨识准则是高斯提出的已得到广泛应用的最小二乘准则;随着现代控制理论和统计理论的发展,又提出了最小方差准则、最大似然准则、贝叶斯准则、H∞准则等辨识准则;辨识理论还证明了各种辨识准则能使辨识所得数学模型渐近趋于真实系统的条件
③辨识算法:对于给定的候选数学模型集,根据辨识准则建立辨识方程组之后,系统辨识问题就化成了一个极值优化计算问题。对于线性系统,应用最小二乘准则,常可得到解析解;对于非线性系统,采用较为复杂的辨识准则,则辨识方程组成为非线性方程组,问题成了含有微分、积分方程的泛函极值问题,无解析解。通常采用迭代算法求解;也可采用逐点递推逼近算法求解
④根据数据处理与现场实际过程的关系,系统辨识分为离线辨识和在线辨识两种。
离线辨识:也称事后处理,先将实验过程中输入 — 输出数据记录下来,实验结束后再进行辨识;由于时间较充裕,记录的信息一般较多,可以适用较复杂的建模问题。
在线辨识:在系统运行中边测量边辨识,一般将辨识结果直接用于系统控制,要求处理信息速度较快,通常采用递推算法,不断用新的测量数据修正当时的估计值,由于计算机处理过程比较耗时,目前还主要用于简单模型的建模。但是随着微机电系统(MEMS)、人工智能、自适应控制等现代控制技术发展,在线辨识的研究和应用将越来越多
⑥开环控制和闭环控制
开环控制:输入信号和输出信号不相关
闭环控制:有反馈信号
⑦系统分析、系统辨识与系统控制
系统分析:已知系统的数学模型,探究系统在各种外作用下的响应历程与表现特性
系统辨识:从已测量得到的外作用和响应历程出发,去确定系统的数学模型
系统控制:已知系统模型,希望规划系统输入,达到期望的系统输出
1.4 方法及分类
①方法
古典方法:脉冲响应法、阶跃响应法、频率响应法、谱分析法、相关分析法
现代方法:最小二乘、广义最小二乘、增广最小二乘、基于神经网络逼近的反向传播算法、基于卷积神经网络的建模算法
②分类
离线辨识:将一定时间内积累的采样数据集中进行一次辨识计算
在线辨识:每个采样周期都根据新的采样数据进行一次递推辨识计算,以节省计算时间和内存空间,及时掌握系统现状
1.5 意义
①作为系统模型,应用于系统仿真、虚拟现实等领域
②预测系统未来的变化趋势。模型一般为动力学方程,给定初始条件下,输出会随着时间而变化,可以预报输出未来的变化趋势
③设计闭环控制器,如内模控制、预测控制、广义预测控制、自校正控制等
1.6 步骤
这里很重要,以下的知识整理部分都是基于这几大块来分类的
①数据获取
系统辨识依赖于系统的输入输出数据集,该数据集通过量测并记录输入与输出实验数据生成,所以需要进行实验设计,例如:输入信号设计、采样区间设计、预采样滤波器设计、数据采集
现场连续运行的系统,且不允许对系统施加实验信号,则记录系统的实际运行数据即可
②模型类选择
确定被辨识系统的数学模型
③参数估计
已知模型的结构后,利用输入输出数据,确定模型中的未知参数。实际测量有误差,一般以统计方法为主:通过设定优化目标,计算出 最佳拟合的统计模型
④模型适用性与有效性检验
通过参数估计的模型,必须进行适用性检验
模型不适用的原因:数据误差过大、代表性太差;模型类选择失误;辨识算法存在问题
模型检验的方法:利用先验知识、利用数据检验(用一组新的数据检验所得到模型的精度)
1.7 课后习题
①什么是系统辨识?
②系统辨识的步骤及三要素
③离线辨识与在线辨识是什么?
④机理建模与系统辨识的优缺点
⑤如何产生并收集系统辨识所需要的数据?
⑥论述二十四节气与农业生产的对应关系
二、数据获取
2.1 持续激励信号
①重要性
好的数据能带来精确的辨识结果,差的数据可能导致错误的辨识结果或者得不到解
简单控制系统可以通过脉冲、阶跃等信号进行分析与设计,但复杂系统(一阶二阶子墨台的和或者乘积)其阶次可能会很高,需要输入信号包含丰富的频谱信息,从而激发出系统的所有模态特征信息。

2.2 白噪声相关
①概率知识
随机过程:n维随机变量按时间组成的一个数组;在每一个时间点上都是一个随机变量,其概率密度函数随时间变化
平稳随机过程:若每个时间点上的概率密度函数都相同
各态遍历平稳随机过程:+时间平均等于集合平均等条件
②白噪声与有色噪声
白噪声是平稳时间序列的一个极端情况,前后时点上的值不相关,功率谱密度为常数,物理上不存在,以下为其定义:
如果一个平稳随机过程,满足均值为0、方差为常数、相互独立且无记忆性,则称为一个白噪声序列,否则为有色噪声序列
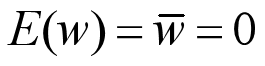
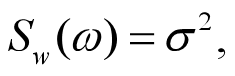 频谱宽度无限
频谱宽度无限
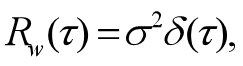
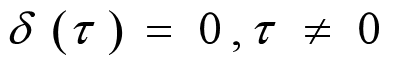
白噪声的用途:
a.用于待辨识函数的激励信号,可以激发系统的全部模态,充分激励;防止数据病态,保证辨识精度;
b.可根据输出的估计误差是否具有白色性来判断辨识方法的优劣,可以判断估计的参数和结构是否合适;
c.可以产生有色噪声
高斯白噪声:
均值为0,方差为1,信号包含从负无穷到正无穷的所有频率分量,且各频率分量的权值相同
③有色噪声
有色噪声是指每一时刻的噪声信号和另一时刻相关,谱密度不为常数,
有色噪声的表示定理:必定存在一个渐近稳定的线性环节,使得在输入为白噪声的情况下,输出有色噪声
2.3 数据病态的原因及解决方法
2.4 数据
一些问题中的数据既是随机变量,又随着时间变化
三、模型类选择
3.1 线性模型
未知系统的阶次————>阶的确定
①取不同的阶比较

②利用残差

已知系统的阶次:
②非参数模型——权函数
所需先验知识少,不会关心系统的阶次、有无滞后,具有噪声时也容易被辨识出来
关于权函数的辨识化为了一个标准的最小二乘估计问题
如果系统稳定,输入信号是持续激励的,则权函数是可以辨识的
③参数化模型——线性差分方程、状态空间方程、传递函数
线性差分方程的辨识可以利用最小二乘估计
3.2 非线性模型
四、参数估计
4.1 最小二乘估计
推导得到的定理,证明估计无偏性及估计误差、噪声方差的定理


一个简单的习题举例:
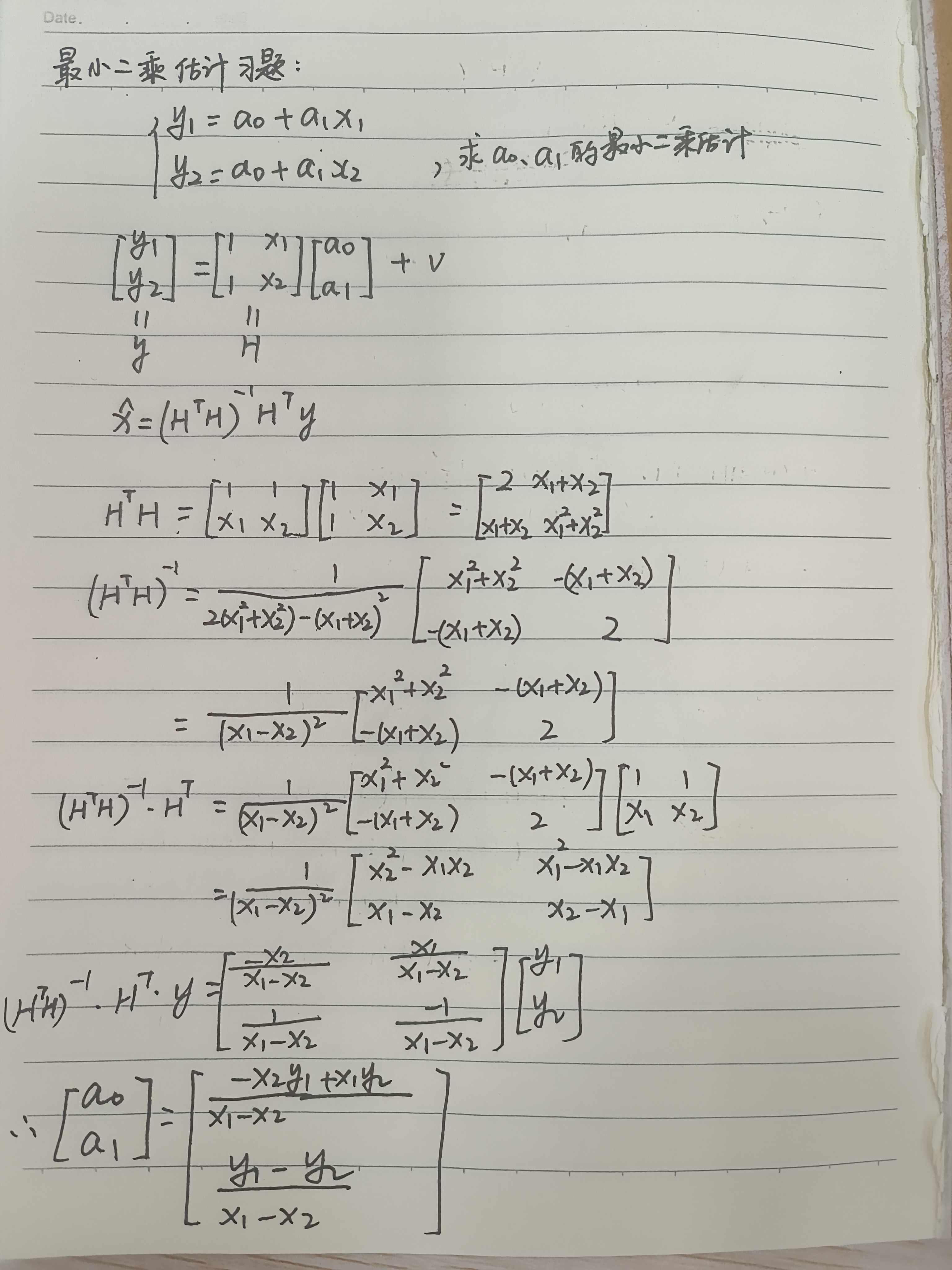
仅考虑测量误差均值大小的影响,没有考虑其概率分布,因此不管观测值质量如何,其对估计值的贡献是一样的
4.2 加权最小二乘估计
在所有加权最小二乘估计中,马尔科夫估计方差最小,也被称为线性最小方差估计

在所有加权最小二乘估计中,马尔科夫估计方差最小,也叫最小方差估计,推导过程如下:




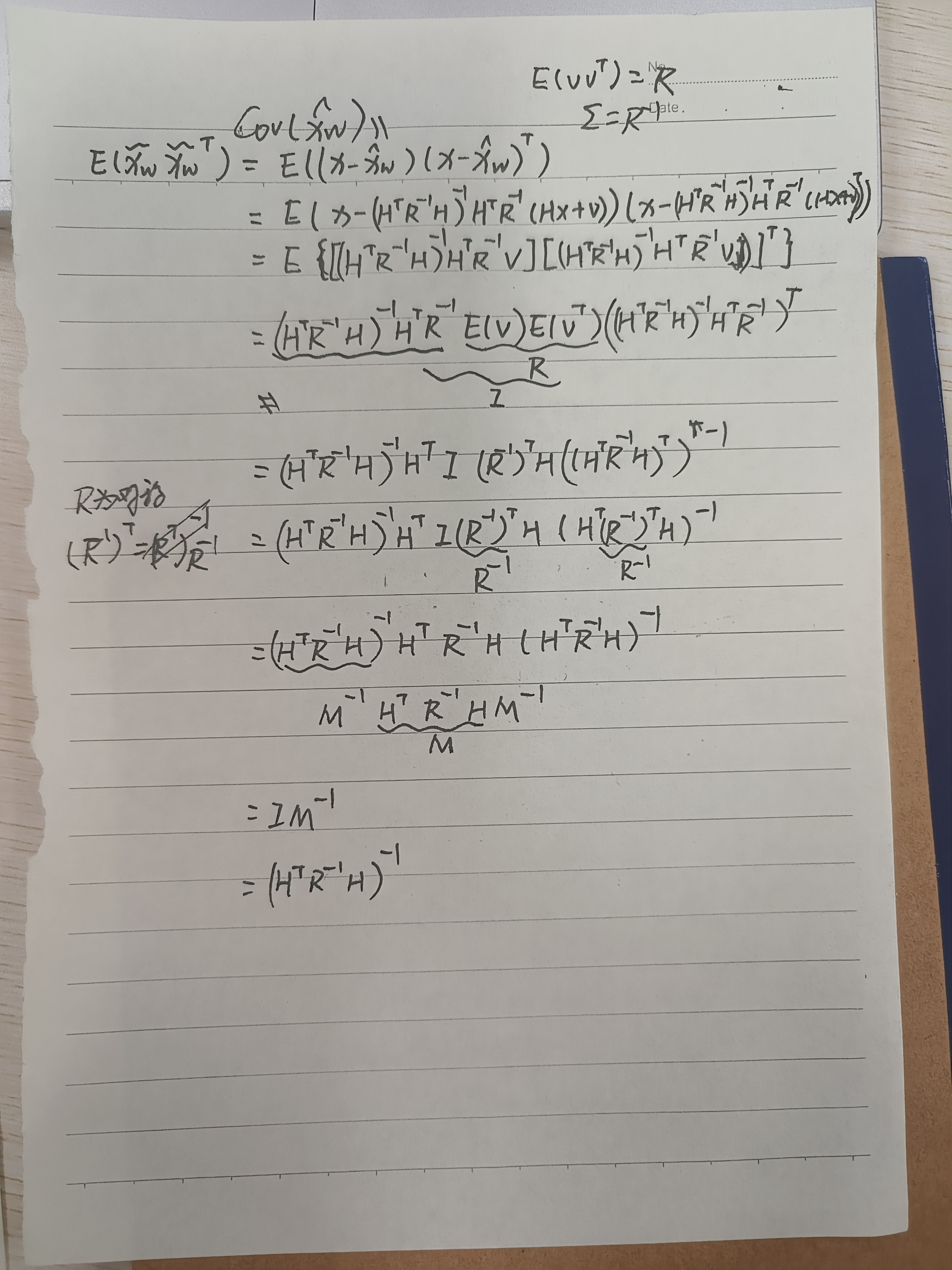
习题:
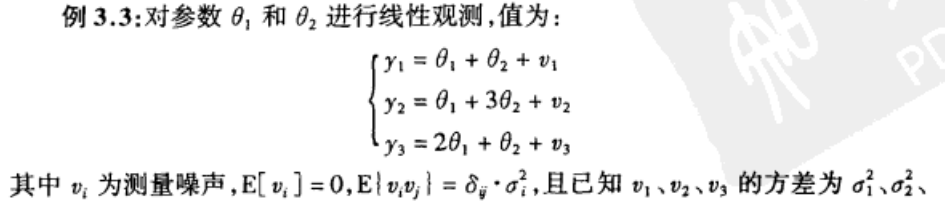
4.3 递推最小二乘估计
推导过程及结论如下:

推导过程如下:

如何选择初始值x0,p0?

估计值(均方收敛于)依概率收敛于x,是相容估计
是强一致收敛估计、会出现数据饱和,具体证明没太看懂,待看
因为数据饱和,采用上乘因子的渐消记忆的递推算法
4.4 加权递推算法
这页指标哪里忘乘了加权系数


4.5 衰减记忆算法

书上有,待推导
4.6 基于广义最小二乘的系统辨识
如果噪声为有色噪声怎么办?没看懂,先记下来吧

4.7 线性最小方差估计
不知道咋分类了,应该是属于这里的

cov(x,y)=cov(y,x)的转置,下图更改错误

证明是最小线性方差估计

综合化简得到定理如下:
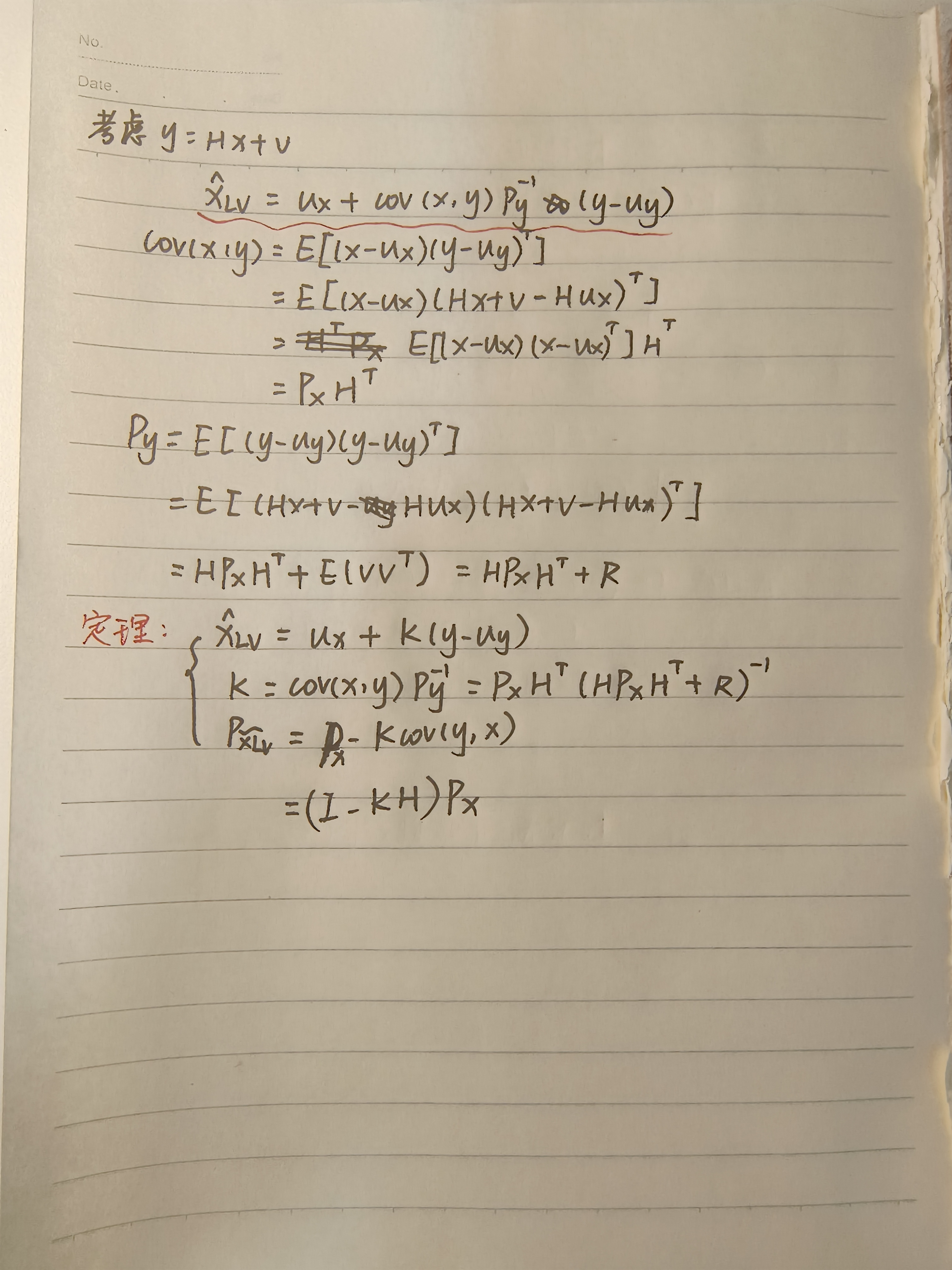
与马尔科夫估计的关系

相关几何性质证明


一个感觉很无语的习题?

五、状态估计
根据测量数据对系统未来的行为进行预报,与参数估计不同的是,状态估计得到的估计量是时间的函数,与参数估计主要的区别是是否利用状态方程?
离线辨识用于滤波和平滑,在线辨识主要是滤波和预报
4.1 最小二乘滤波
仅考虑测量误差均值的影响,未考虑其概率的分布,过程中的噪声的先验知识也未体现,扰动在递推过程无法消除,故仅仅在状态信息较少的时候才采用最小二乘滤波

4.2 最优滤波



4.3 卡尔曼滤波
直接推导法:



定理如下:

六、数学基本知识
2.1 状态空间相关
①状态空间方程
输入变量:外部施加到系统上的全部激励,包括控制信号U(t),过程噪声W(t)
输出变量:能从外部观测或是内部测量得到的来自系统的信息,Y(t) y
状态变量:完全描述系统行为的最小变量组X(t)=[x1(t) x2(t) ...... ],连续系统、离散系统,
②状态空间表达式
状态方程,描述系统状态变量和输入变量的方程组
输出方程,描述输出变量和状态变量、输入变量的关系
通用形式如下:
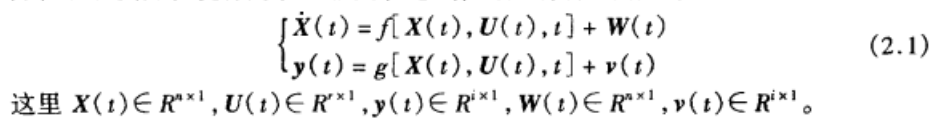
线性形式如下:

如何建立?基本形式很简单
含输入信号导数项的见现代工程控制理论,如下:

③ 状态转移矩阵
线性定常非齐次状态方程如下,初始状态为0,初始时刻为0
![]()
推导过程如下

如何求,推导过程如下:



状态转移矩阵的求法如下:

2.2 离散化及连续化
在平衡点附近做近似处理,李雅普诺夫提出的需要满足的条件,局部稳定 or 大范围渐近稳定?
连续系统离散化,及其逆过程

2.3 随机变量及随机事件
这里参考概率论
七、习题
期末考试的题型参考
1.简单概念
①什么是系统辨识?其三要素是什么?
②白噪声有色噪声的定义,如何将有色噪声白化?
③什么是持续激励信号,其作用是什么?
④卡尔曼滤波的Q和R对滤波结果的影响是什么?
⑤数据病态的原因及解决方法
2.标准最小二乘估计
第二问是问了残差的平方和,不太会答,不确定
3.加权最小二乘估计和
考了加权和马尔科夫估计,新奇的是H=1,非常好计算,
4.递推最小二乘
①利用双线性变换()得到G(z)表达式
②利用递推最小二乘估计参数的值,这里我们的题要求算3次递推,非常难算啊,公式也要背

5.卡尔曼滤波
给出具体方程和噪声方差如下:
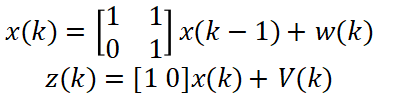
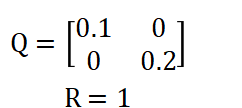
根据卡尔曼滤波公式,求k=1的公式更新情况,求下列值
(1)、
(2)增益矩阵,
(3)
解:列出以下公式(题目不给出,要背),计算即可
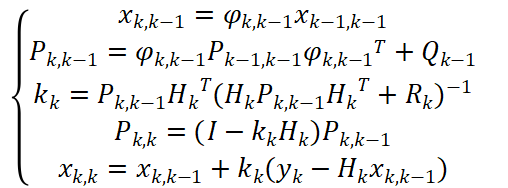
八、卡尔曼滤波代码
MATLAB,大作业仅供参考
student_number_last_two=22;
N=200-student_number_last_two;%生成过程噪声
if exist('w_k.mat', 'file')
load('w_k.mat', 'w_k');
mean(w_k,2);%验证
A=var(w_k,0,2);%采用无偏估计,按行计算
Qk=[A(1) 0;0 A(2)]%使用真实生成的方差作为Qk
else
% 文件不存在,生成并保存新数据
Q=0.5*eye(2)
w_k = mvnrnd(zeros(2, N)', Q)';
save('w_k.mat', 'w_k');
fprintf('已生成新数据并保存至 %s\n', 'w_k.mat')
end%生成观测噪声
if exist('V_k.mat', 'file')
load('V_k.mat', 'V_k');
Rk=var(V_k,0,2);
mean(V_k);%
else
R=1;
V_k = mvnrnd(zeros(1, N)', R)';
save('V_k.mat', 'V_k');
fprintf('已生成新数据并保存至 %s\n', 'V_k.mat')
end%初始化状态序列
x_true=zeros(2,N);
x_true(:,1)=[0 ; 5];%初始值
T=1;%采样周期
% 迭代生成真实状态数据,依据状态方程 x(k) = [1 T; 0 1]*x(k-1) + w(k) 计算
for k = 2:N
x_true(:, k) = [1 T; 0 1] * x_true(:, k - 1) + w_k(k);
end%初始化观测序列
z=zeros(1,N);
z_v=zeros(1,N);
%迭代生成观测数据
for k = 1:N
z(k) = [1 0] * x_true(:,k) + V_k(k);
z_v(k)=[0 1] * x_true(:,k) + V_k(k);
end%卡尔曼滤波计算
phi=[1 T;0 1];
x=zeros(2,N);
H=[1 0];
P=zeros(2,2,N);
P(:,:,1)=10*eye(2);
for k=2:N
x_k_k1= phi * x(:,k-1);
P_k_k1=phi*P(:,:,k-1)*phi'+Qk;
k_k=P_k_k1*H'*inv(H*P_k_k1*H'+Rk);
P(:,:,k)=P_k_k1-k_k*H*P_k_k1;
x(:,k)=x_k_k1+k_k*(z(k)-H*x_k_k1);
end% 可视化部分
figure(1);
plot(x_true(1,1:N), 'b-', 'LineWidth', 1.5); %绘制真实位置状态,蓝色实线
hold on;
plot(z, 'r--', 'LineWidth', 1); % 绘制观测的位置数据,红色虚线
plot(x(1,:), 'g-.', 'LineWidth', 1.8); % 绘制滤波估计位置轨迹,绿色点划线
legend('真实位置数据', '观测位置数据','滤波估计位置数据');
title('位置的真实状态、观测及滤波预测对比图');
xlabel('状态序列k');
ylabel('位置');
grid on;九、最小二乘代码
仅供参考
y(1)=0;
y(2)=0;
x(:,1)=[1.642 0.715 0.39 0.35]';
ts=0.001;
v=randn(1,200)*sqrt(0.5);
K=zeros(4,203);
L=0.9;
for k=1:200u(k)=sin(k*ts);end
P(:,:,1)=eye(4);
for k=3:200H=[-y(k-1) -y(k-2) u(k-1) u(k-1)];y(k)=H *x(:,k-2)+v(k);P(:,:,k-1)=(1/L)*(eye(4)-K(:,k-1)*H*P(:,:,k-2));K(:,k-1)=P(:,:,k-2)*H'*inv(L*eye(1)+H*P(:,:,k-2)*H');x(:,k-1)=x(:,k-2)+K(:,k-1)*(y(k-1)-H*x(:,k-2));end
plot(x(1,:))
plot(x(2,:))
