C语言计算n个矩阵乘法

在线性代数学科中，矩阵的乘法是一项计算量较大的重要内容。本程序旨在计算两个或者多个矩阵相乘的结果。

数学原理

矩阵的乘法有结合律，没有分配律。因此，即使有再多的矩阵相乘，只需按顺序先将两个相乘，再将所得的矩阵与下一个矩阵相乘，以此类推，即可得到结果。
两个矩阵相乘时，要求前一个矩阵的列数与后一个矩阵的行数相等。因此，多个矩阵相乘后最终得到的矩阵的行数等于第一个矩阵的行数，列数等于最后一个矩阵的列数。
A、B两个矩阵相乘得到的矩阵C中每一个元素的计算公式如下：
$$c_{ij}=\sum _{k=1}^n{a}_{ik}{b}_{kj}=a_{i1}{b}_{1j}+a_{i2}{b}_{2j}+\cdots +a_{in}{b}_{nj}$$

完整代码

#include <stdio.h>int find_max(int list[], int size) {int max = 0;for (int k = 0; k < size; k++) {if (list[k] > max) {max = list[k];}}return max;
}int main() {int n;printf("the number of matrices: ");scanf("%d", &n);int scale[2][n];for (int m = 0; m < n; m++) {printf("the number of row(s) and column(s) of matrix %d: ", m + 1);scanf("%d %d", &scale[0][m], &scale[1][m]);}for (int m = 0; m < n - 1; m++) {if (scale[1][m] != scale[0][m+1]) {printf("The matrix multiplication is illegal!");return 0;}}int rmax = find_max(scale[0], n), cmax = find_max(scale[1], n);int mat[n][rmax][cmax];for (int m = 0; m < n; m++) {printf("\nmatrix %d:\n", m + 1);for (int i = 0; i < scale[0][m]; i++) {printf("row %d: ", i + 1);for (int j = 0; j < scale[1][m]; j++) {scanf("%d", &mat[m][i][j]);}}}int tempmat[n][rmax][cmax];int r = scale[0][0], c = scale[1][n-1];int t;for (int i = 0; i < r; i++) {for (int j = 0; j < scale[1][0]; j++) {tempmat[0][i][j] = mat[0][i][j];}}for (int m = 0; m < n - 1; m++) {for (int leftr = 0; leftr < r; leftr++) {for (int rightc = 0; rightc < scale[1][m+1]; rightc++) {t = 0;for (int k = 0; k < scale[0][m+1]; k++) {t += tempmat[m][leftr][k] * mat[m+1][k][rightc];}tempmat[m+1][leftr][rightc] = t;}}}printf("\nresult:");for (int i = 0; i < r; i++) {printf("\nrow %d: ", i + 1);for (int j = 0; j < c; j++) {printf("%d ", tempmat[n-1][i][j]);}}return 0;
}

代码解释

下面对代码进行逐段解释。

寻找数组中最大值函数find_max

int find_max(int list[], int size) {int max = 0;for (int k = 0; k < size; k++) {if (list[k] > max) {max = list[k];}}return max;
}

该函数的功能是遍历数组元素，找出数组list中的最大值，在后续设定数组长度时需要用到，以确保能装得下所有元素。

主函数Part1：输入行数、列数，判断可行性

int n;
printf("the number of matrices: ");
scanf("%d", &n);int scale[2][n];
for (int m = 0; m < n; m++) {printf("the number of row(s) and column(s) of matrix %d: ", m + 1);scanf("%d %d", &scale[0][m], &scale[1][m]);
}for (int m = 0; m < n - 1; m++) {if (scale[1][m] != scale[0][m+1]) {printf("The matrix multiplication is illegal!");return 0;}
}

n指的是相乘的矩阵的个数，之后需要用户输入每个矩阵的行数和列数，并先根据行数和列数判断矩阵相乘是否有意义。具体来说，即任何两个相邻的矩阵都要满足前一个矩阵的列数等于后一个矩阵的行数。如果存在不满足该条件的矩阵，则程序中止。
用户输入的行数和列数存储在二维数组scale中，第一个维度为0时表示各个矩阵的行数，为1时表示列数。

主函数Part2：输入矩阵元素

int rmax = find_max(scale[0], n), cmax = find_max(scale[1], n);int mat[n][rmax][cmax];
for (int m = 0; m < n; m++) {printf("\nmatrix %d:\n", m + 1);for (int i = 0; i < scale[0][m]; i++) {printf("row %d: ", i + 1);for (int j = 0; j < scale[1][m]; j++) {scanf("%d", &mat[m][i][j]);}}
}

mat是一个三维数组，第一个维度是矩阵的编号，后两个维度分别是矩阵的行和列。用户需要根据提示输入各个矩阵每个元素的值。

主函数Part3：进行矩阵的乘法

int tempmat[n][rmax][cmax];int r = scale[0][0], c = scale[1][n-1];int t;for (int i = 0; i < r; i++) {for (int j = 0; j < scale[1][0]; j++) {tempmat[0][i][j] = mat[0][i][j];}}for (int m = 0; m < n - 1; m++) {for (int leftr = 0; leftr < r; leftr++) {for (int rightc = 0; rightc < scale[1][m+1]; rightc++) {t = 0;for (int k = 0; k < scale[0][m+1]; k++) {t += tempmat[m][leftr][k] * mat[m+1][k][rightc];}tempmat[m+1][leftr][rightc] = t;}}}

tempmat三维数组用来临时存储矩阵。其中，规定tempmat的第0项等于mat的第0项，之后每次相乘都是tempmat的第m项和mat的第m+1项相乘，得到的结果存储在tempmat的第m+1项中。全部乘完后，最后结果即为tempmat的第n-1项（最后一项）。本程序的矩阵乘法计算公式即为乘法定义的公式（见“数学原理”部分）。

主函数Part4：输出结果

printf("\nresult:");
for (int i = 0; i < r; i++) {printf("\nrow %d: ", i + 1);for (int j = 0; j < c; j++) {printf("%d ", tempmat[n-1][i][j]);}
}

运行结果示例

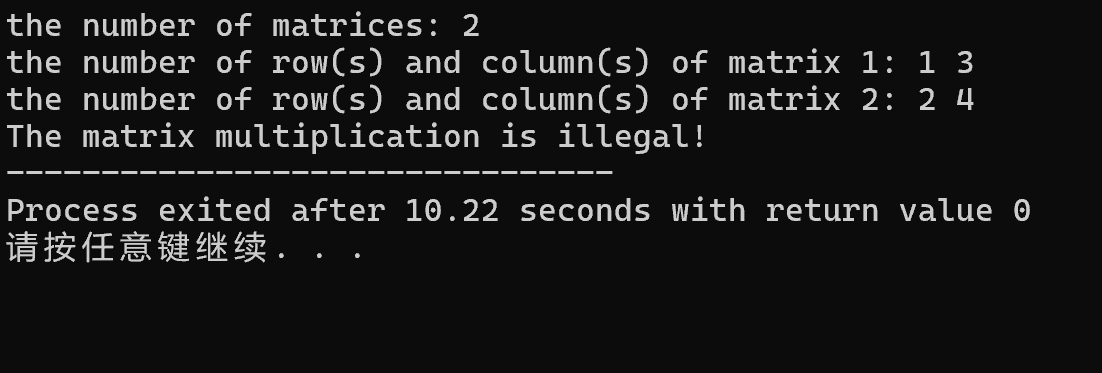
当输入的行数、列数不符合规范时，程序会及时中止，例如：

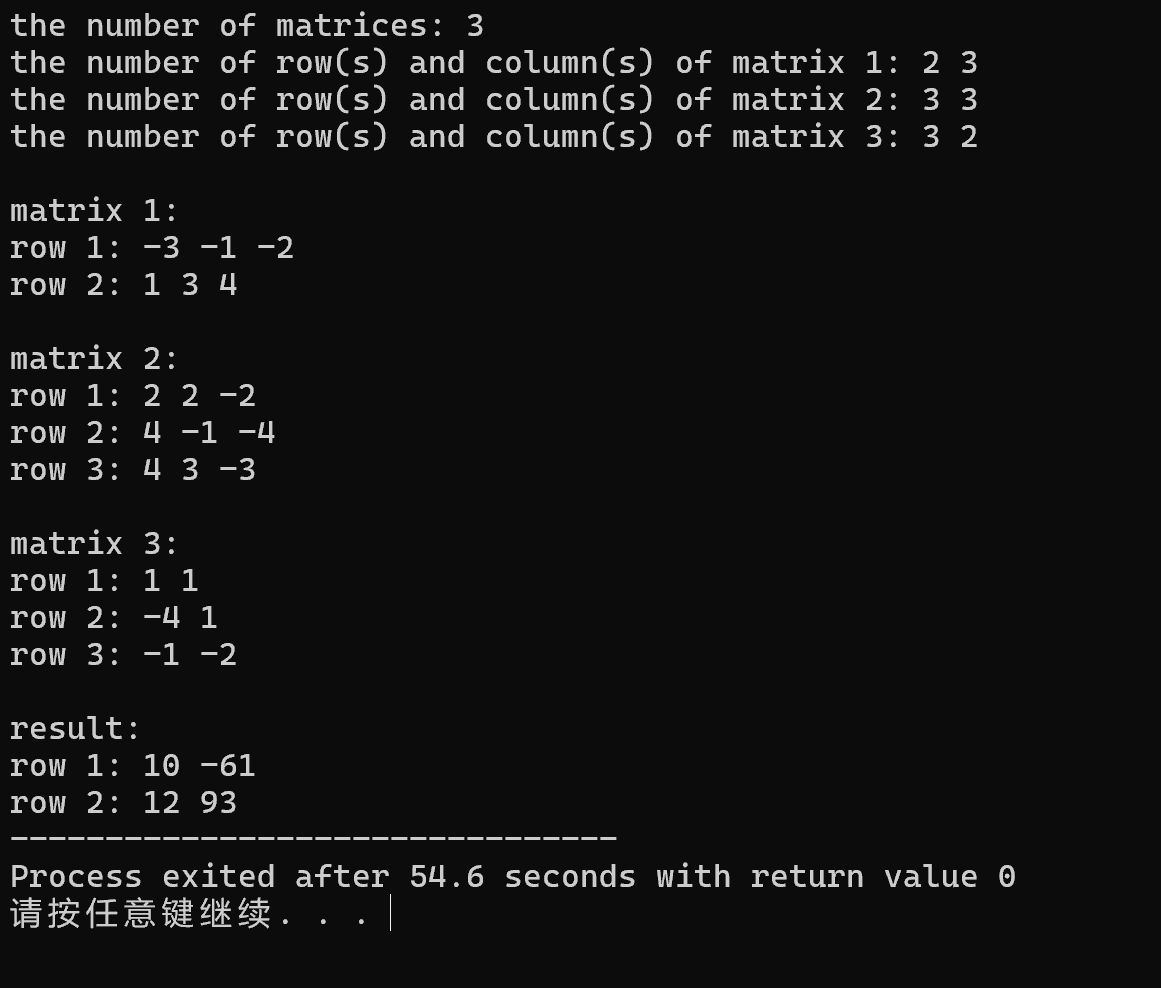
以下是一个矩阵相乘的正确计算结果：