当前位置： 首页 > news >正文

leetcode460.LFU缓存

news 2025/10/3 6:32:09

设计 LFU 缓存的核心思路，本质是从问题需求倒推数据结构选择，再通过组合结构解决单一结构的缺陷，整个思考过程可以拆解为以下几个关键步骤：

第一步：明确 LFU 的核心需求 ——“淘汰规则” 决定必须跟踪的信息

LFU 的核心规则是：优先淘汰使用频率最低的元素；若频率相同，淘汰最久未使用的元素。这意味着我们必须同时跟踪两个维度的信息：

  1. 每个元素的 “使用频率”（用于判断 “谁最不经常使用”）；
  2. 同一频率下元素的 “最近使用时间”（用于频率相同时判断 “谁最久未使用”）。

这两个维度缺一不可，且所有操作（查找、更新频率、淘汰）都需要高效（题目要求 O (1) 平均时间复杂度）。

第二步：拆解需求，逐个解决 “单一维度” 的问题

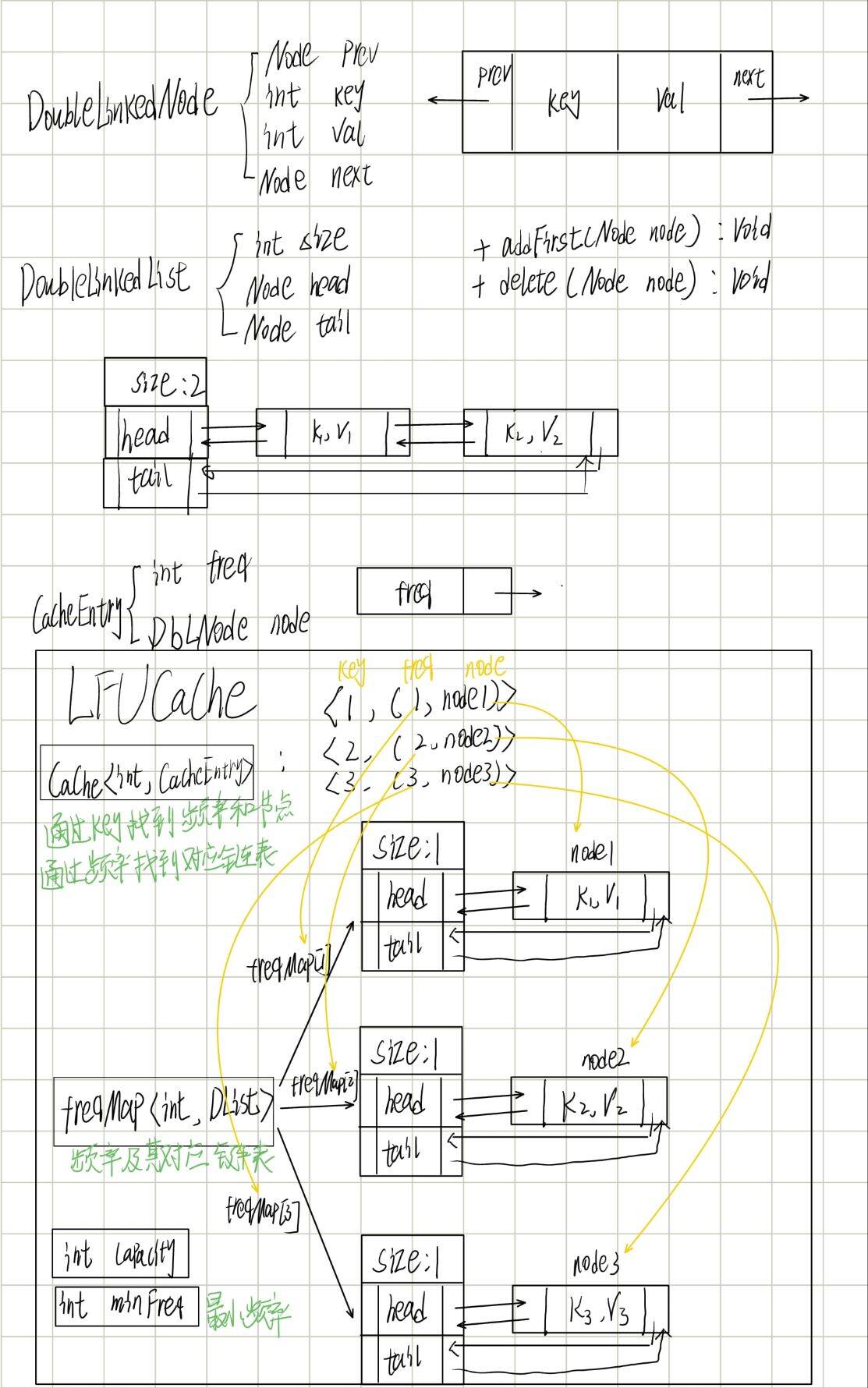
问题 1：如何高效跟踪每个元素的 “使用频率”？
  • 最直接的想法：给每个元素绑定一个 “频率计数器”，访问 或者 插入时 + 1。但仅这样还不够 —— 我们需要快速找到 “频率最低的一组元素”（否则淘汰时要遍历所有元素，效率太低）。
  • 优化思路：按频率 “分组” 管理元素。比如，频率为 1 的元素放一组，频率为 2 的放另一组…… 这样找 “最低频率” 时，只需定位到最小的频率组即可。
  • 数据结构匹配：用哈希表（freqMap） 实现 “频率→元素组” 的映射（key = 频率，value = 该频率下的所有元素）。哈希表的查找是 O (1)，能快速定位某一频率对应的元素组。
问题 2：如何高效跟踪 “同一频率下元素的最近使用时间”？
  • 同一频率组内，需要区分 “最近使用” 和 “最久未使用”（淘汰时取最久未使用的）。这本质是 “维护一个动态顺序”：每次访问元素，要把它标记为 “最近使用”（移到顺序的前端）；淘汰时取 “最久未使用”（顺序的末端）。
  • 数据结构匹配：双向链表是最佳选择。因为：
    • 已知节点时，插入（移到头部）和删除（从链表中移除）的时间复杂度是 O (1)（单向链表做不到，因为找不到前驱节点）；
    • 链表的 “头部” 天然可以表示 “最近使用”，“尾部” 表示 “最久未使用”，符合需求。
问题 3：如何快速定位元素的 “频率” 和 “所在链表的节点”？
  • 当我们访问一个 key 时，需要先找到它的频率（才能知道从哪个频率组移除），以及它在链表中的具体节点（才能执行移到头部等操作）。如果每次都遍历链表查找，时间复杂度会退化为 O (n)，不符合要求。
  • 数据结构匹配：再用一个哈希表（cache） 实现 “key→（频率 + 节点）” 的映射。key 是缓存的键，value 是一个结构体（CacheEntry），存储该 key 的频率和在链表中的节点引用。这样通过 key 能直接拿到频率和节点，实现 O (1) 定位。
问题 4：如何快速找到 “当前最小频率”？
  • 有了freqMap按频率分组后，还需要一个变量记录 “当前最小的频率”（minFreq），否则每次淘汰时要遍历freqMap的所有 key 找最小值（O (k)，k 是频率种类），效率太低。
  • 维护逻辑：
    • 新元素插入时，频率为 1，所以minFreq直接设为 1；
    • 当某一频率组的元素全部移走（链表为空），且该频率等于minFreq时，minFreq递增（因为原最小频率的元素已不存在）。

第三步：组合结构，解决 “操作流程” 的闭环

单一结构只能解决局部问题，需要把上述结构组合起来，形成完整的操作流程：

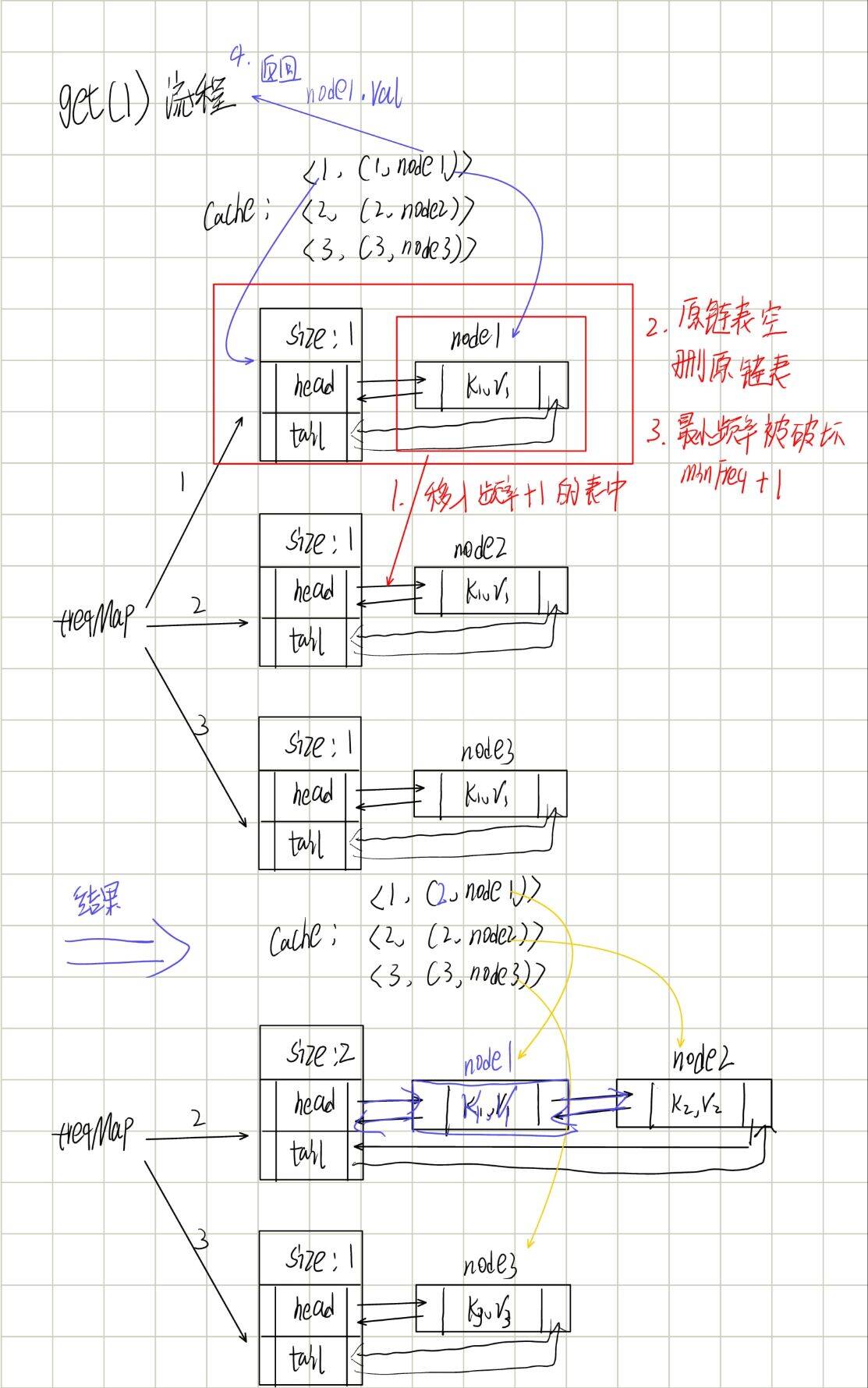
  • get 操作（访问元素）：

    1. 用cache找到 key 对应的频率和节点（O (1)）；
    2. 从freqMap中该频率的链表中删除节点（O (1)）；
    3. 若链表为空，删除该频率并更新minFreq（O(1)）；
    4. 频率 + 1，将节点加入新频率的链表头部（O (1)）。

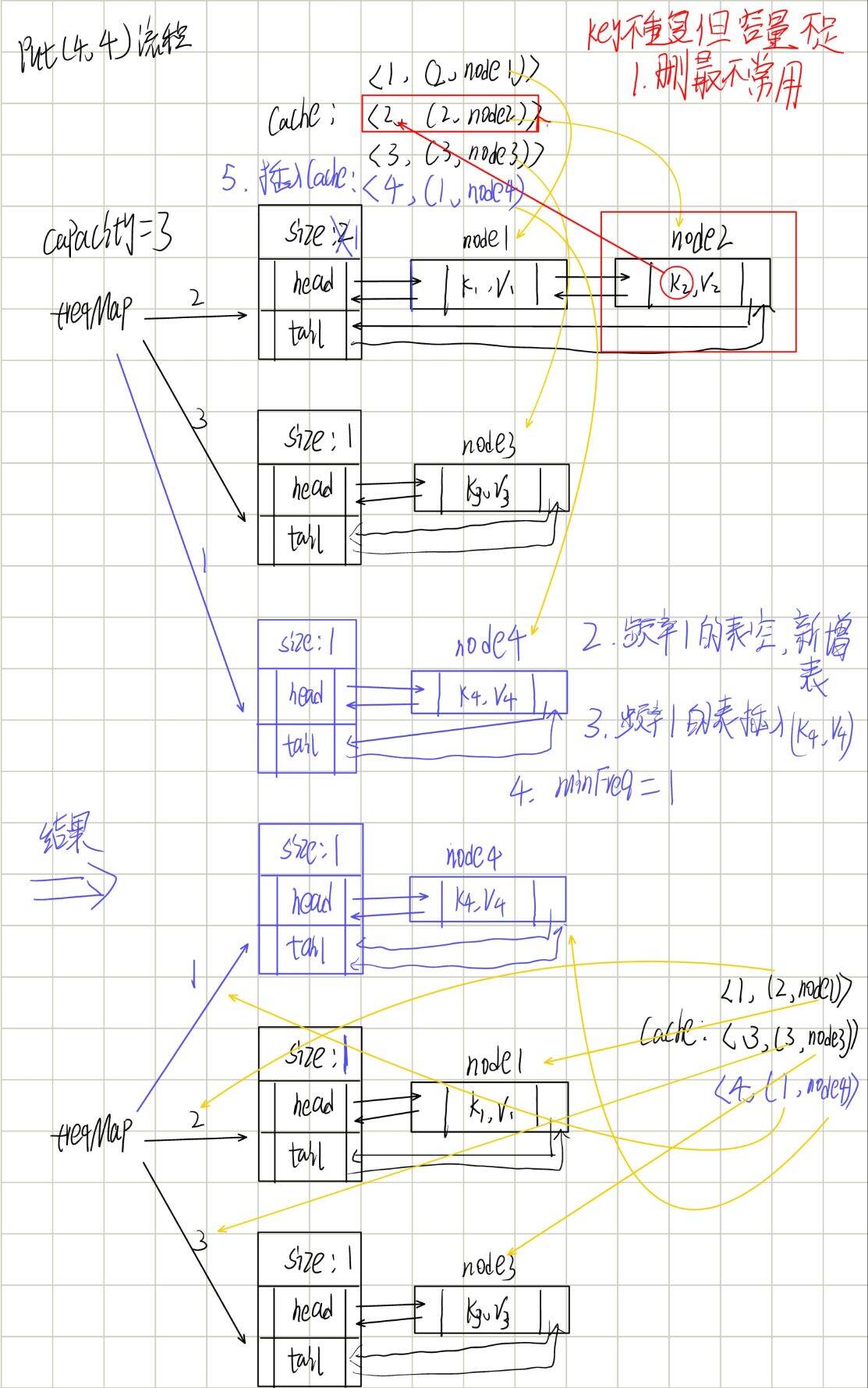
  • put 操作（插入 / 更新元素）：

    • 若 key 已存在：流程同 get（更新频率），额外修改节点的 value；
    • 若 key 不存在：
      1. 若缓存满，用minFreq找到对应链表，删除尾部节点（最久未使用），并从cache中移除（O (1)）；
      2. 新建节点，频率设为 1，加入cache和频率 1 的链表头部，minFreq设为 1（O (1)）。

第四步：细节优化，解决 “边界问题”

  • 哨兵节点：双向链表的head和tail哨兵节点，避免了 “空链表增删节点” 的复杂判断（比如addFirst时无需检查链表是否为空）；
  • 封装内部类：用DoubleLinkedNode存储 key/value 和指针，DoubleLinkedList封装链表操作，CacheEntry关联频率和节点，让逻辑更清晰，避免散落在外部类中；
  • computeIfAbsent简化代码：创建新频率的链表时，用哈希表的computeIfAbsent直接替代 “判断是否存在→不存在则创建→插入” 的三步操作，减少冗余。

总结：思路的本质是 “需求→结构→组合→优化”

整个设计思路的核心逻辑是：

  1. 从 LFU 的淘汰规则（频率 + 最近使用）出发，明确需要跟踪的信息；
  2. 为每个信息维度匹配最合适的数据结构（哈希表解决快速查找 / 分组，双向链表解决顺序维护）；
  3. 用变量（minFreq）和辅助结构（CacheEntry）连接各个数据结构，形成闭环操作；
  4. 通过细节优化（哨兵节点、封装）降低复杂度，确保所有操作达到 O (1)。

这种思路不是凭空产生的，而是基于对 “数据结构特性” 的理解（哈希表的 O (1) 查找、链表的顺序维护），以及对 “问题需求” 的拆解（必须同时处理频率和时间两个维度），最终形成的最优组合方案。

class LFUCache {private class DoubleLinkedNode {private DoubleLinkedNode prev;private int key;private int value;private DoubleLinkedNode next;public DoubleLinkedNode() {}public DoubleLinkedNode(int key, int value) {this.key = key;this.value = value;}}private class DoubleLinkedList {private int size;private DoubleLinkedNode head;private DoubleLinkedNode tail;public DoubleLinkedList() {//1.初始化成员变量head = new DoubleLinkedNode();tail = new DoubleLinkedNode();//2.将头尾节点相互连接head.next = tail;tail.prev = head;}public void addFirst(DoubleLinkedNode doubleLinkedNode) {size++;doubleLinkedNode.prev = head;doubleLinkedNode.next = head.next;head.next.prev = doubleLinkedNode;head.next = doubleLinkedNode;}public void delete(DoubleLinkedNode doubleLinkedNode) {size--;doubleLinkedNode.prev.next = doubleLinkedNode.next;doubleLinkedNode.next.prev = doubleLinkedNode.prev;}}private class CacheEntry {private int freq;private DoubleLinkedNode node;public CacheEntry(int freq, DoubleLinkedNode node) {this.freq = freq;this.node = node;}}private int capacity;private int minFreq;private Map<Integer, DoubleLinkedList> freqMap;private Map<Integer, CacheEntry> cache;public LFUCache(int capacity) {this.capacity = capacity;freqMap = new HashMap<>();cache = new HashMap<>();}public int get(int key) {//1.如果key不存在直接返回-1if (!cache.containsKey(key)) {return -1;}//2.根据key得到cache中的cacheEntryCacheEntry cacheEntry = cache.get(key);//3.根据cacheEntry中的freq具体确定在那个频率双向链表，根据node确定双向链表中的具体节点DoubleLinkedList oldList = freqMap.get(cacheEntry.freq);//4.将这个频率对应的双向链表中的该节点删除oldList.delete(cacheEntry.node);//4.1若删除后旧表空了，把旧表从freqMap移除if (oldList.size == 0) {freqMap.remove(cacheEntry.freq);//4。2若旧表的频率就是最小频率，那么最小频率此时就要更新（+1）if (minFreq == cacheEntry.freq) {minFreq++;}}//5.更新频率，把访问的节点的频率+1，在新频率对应的表中插入这个nodefreqMap.computeIfAbsent(++cacheEntry.freq, k->new DoubleLinkedList()).addFirst(cacheEntry.node);//6.返回数据return cacheEntry.node.value;}public void put(int key, int value) {//1.如果key已经存在了，那么和get方法的步骤类似，差别在于需要更改node中的value值if (cache.containsKey(key)) {//1.1根据key拿到cache中的cacheEntry（这里面可看到访问频率，和访问的具体节点）CacheEntry cacheEntry = cache.get(key);//1.2删除这个频率对应的链表中的nodeDoubleLinkedList oldList = freqMap.get(cacheEntry.freq);oldList.delete(cacheEntry.node);//1.2.1若删除后旧表空了，把旧表从freqMap移除if (oldList.size == 0) {freqMap.remove(cacheEntry.freq);//1.2.2若旧表的频率就是最小频率，那么最小频率此时就要更新（+1）if (minFreq == cacheEntry.freq) {minFreq++;}}//1.3更新频率，把访问的节点的频率+1，把node的值更新，在新频率中的表中插入这个nodecacheEntry.node.value = value;freqMap.computeIfAbsent(++cacheEntry.freq, k -> new DoubleLinkedList()).addFirst(cacheEntry.node);return;}//2.如果达到容量上限，需要淘汰最不经常使用的cache块(最小频率对应的链表中的末尾节点)if (cache.size() == capacity) {//2.1最小频率对应的链表中的最后一个节点DoubleLinkedList oldList = freqMap.get(minFreq);DoubleLinkedNode tailNode = oldList.tail.prev;cache.remove(tailNode.key);oldList.delete(tailNode);//2.2若删除后该链表空了，freqMap把该链表移除if (oldList.size == 0) {freqMap.remove(minFreq);}}//3.更新最小频率为1，并新增一个node放到freq为1对应的链表和cache中minFreq = 1;DoubleLinkedNode node = new DoubleLinkedNode(key, value);cache.put(key, new CacheEntry(1, node));freqMap.computeIfAbsent(1, k -> new DoubleLinkedList()).addFirst(node);}
}/*** Your LFUCache object will be instantiated and called as such:* LFUCache obj = new LFUCache(capacity);* int param_1 = obj.get(key);* obj.put(key,value);*/

http://www.dtcms.com/a/434645.html

相关文章：

  • 如何进入网站后台管理网站信用中国 网站截图怎么做
  • 百度网站推广电话数据分析师资格证书
  • 高低点通道突破策略
  • 【ROS2学习笔记】服务
  • 建站是什么东西建公司网站需要自己有系统吗
  • Leetcode热题100（8-12）
  • 六站合一的优势123上网之家网址
  • C++中的多线程编程及线程同步
  • 湛江做网站从微信运营方案
  • 伊吖学C笔记（8、结构体、链表、union、enum、typedef）
  • 2022 年真题配套词汇单词笔记（考研真相）
  • HTML5消费收入矩阵计算器
  • 霸州做阿里巴巴网站庆安建设局网站
  • PCB学习——STM32F103VET6-STM32主控部分
  • 大学生作业做网站网站建设公司比较
  • 写一个星河社区aistudio大模型部署之后的AI agent转发程序
  • 网站上的中英文切换是怎么做的wordpress页面移动端
  • 八、Scala 集合与函数式编程
  • 腾讯CODING Maven的aar制品添加上传流程
  • Effective Modern C++ 条款29: 移动语义的局限性与实践指南
  • 2025年渗透测试面试题总结-98（题目+回答）
  • 深圳网站制作 公司wordpress备份百度云
  • 《时序数据监控平台优化指南：从查询超时到秒级响应，指标下的存储与检索重构实践》
  • 新版android studio创建项目的一些问题
  • 做企业网站有哪些好处软件技术买什么笔记本好
  • 【Redis】Redis的5种核心数据结构和实战场景对应（在项目中的用法）
  • Vue 与 React 深度对比：技术差异、选型建议与未来趋势
  • 创意网站页面wordpress预约小程序
  • Android_framework-odex优化
  • RAG核心特性：文档过滤和检索