地学:GAM RF 教程
01
数据预处理
所有栅格数据处理的第一步就是对齐行列号,保证多源影像严格匹配;检查影像完整性,快速发现异常。
用户参数设置
input_dir = r"E:/deal"output_sub = 'aligned_output'FORMATS = ('tif', 'tiff', 'img', 'bil', 'vrt')
收集所有栅格文件
patterns = [s.path.join(input_dir, f'**/*.{ext}') for ext in FORMATS]raster_paths = []for pat in patterns:raster_paths.extend(glob.glob(pat, recursive=True))
扫描输入目录,收集所有符合指定格式的栅格文件路径,保证不同影像都能被统一处理。
打印文件的坐标系(CRS)
for p in raster_paths:with rasterio.open(p) as src:print(f" {os.path.basename(p)} -> {src.crs}")
打印每个影像的坐标系,方便检查数据来源是否一致。
选择参考影像
def find_smallest(paths):...ref_path = find_smallest(raster_paths)
在所有影像中选择 像素数最小 的作为参考影像(避免无谓的数据量膨胀)。提取它的 尺寸、分辨率、变换矩阵、CRS,用作对齐基准。
创建输出目录
output_dir = os.path.join(input_dir, output_sub)os.makedirs(output_dir, exist_ok=True)
自动建一个存放对齐结果的文件夹,不会覆盖原始数据。
对齐所有栅格影像
with rasterio.open(src_path) as src:profile = src.profile.copy()profile.update({...})with rasterio.open(dst_path, 'w', **profile) as dst:for i inrange(1, src.count + 1):reproject(...)
结果提示
print(f"\n完成!所有对齐后的影像已保存至:{output_dir}")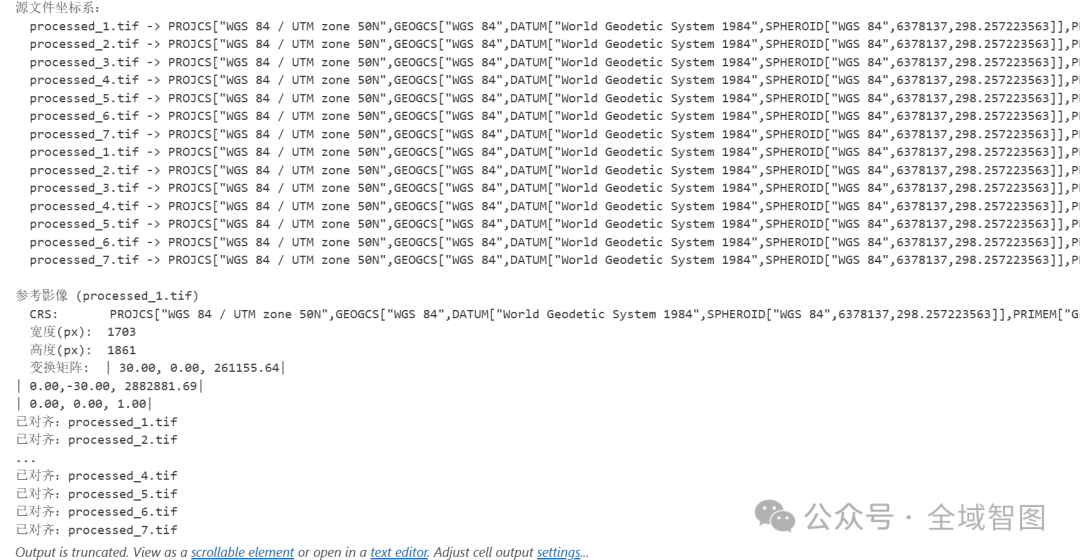
02
相关性分析
绘制变量相关系数热力图,直观展示变量间的线性关系。
设置绘图环境
sns.set(yle="white", font="SimHei", font_scale=1.2)plt.rcParams['axes.unicode_minus'] = False
设置 Seaborn 的整体风格,指定中文字体(SimHei),并解决负号显示问题。
计算相关系数与显著
from scipytats import pearsonrcorr = np.zeros((n, n))pvals = np.zeros((n, n))for i in range(n):for j in range(n):r, p = pearsonr(df[cols[i]], df[cols[j]])corr[i, j] = rpvals[i, j] = p
遍历所有变量组合,计算 Pearson 相关系数 和 p 值。
显著性标记函数
defsignificance_marker(p):if p < 0.001:return"***"elif p < 0.01:return"**"elif p < 0.05:return"*"else:return""
构建注释矩阵
# 下三角显示相关系数,上三角显示显著性符号
为热力图准备显示内容:
下三角显示相关系数数值(带颜色映射)
上三角显示显著性符号(黑色标注)
对角线留空
绘制相关系数热力图
mask = np.triu(np.ones_like(corr_df, dtype=bool))sns.heatmap(corr_df, mask=mask, annot=annot, ...)
下三角:相关系数(带色块)
*
**
***
结果就是一个 直观的变量相关性矩阵。
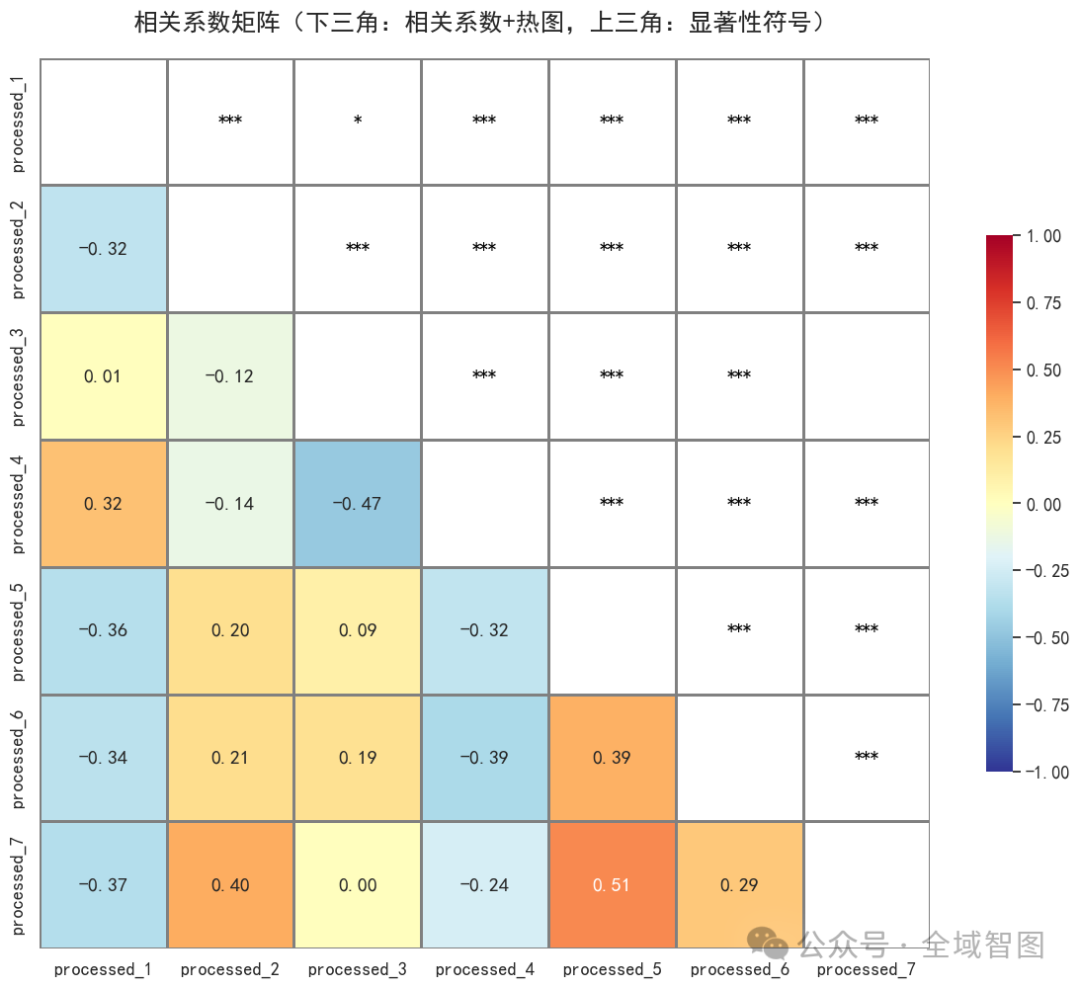
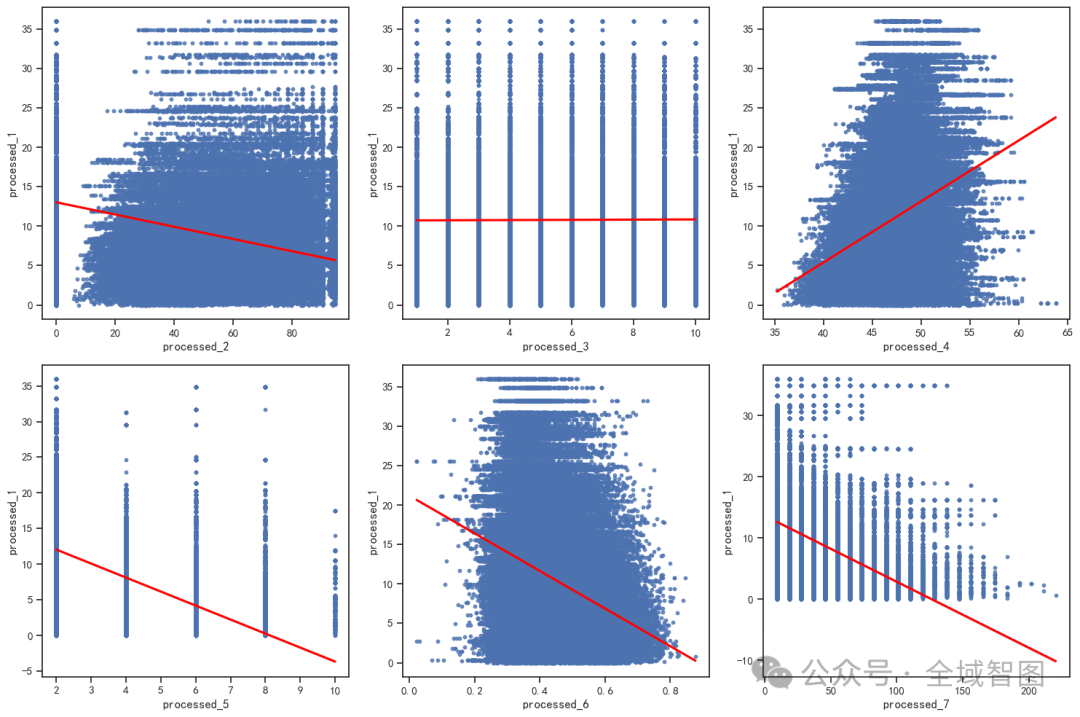
变量两两关系散点矩阵
随机抽样 500 行数据,绘制 Pairplot(散点图矩阵):
每个子图展示两个变量之间的散点分布
对角线上展示核密度估计(KDE)分布
可以直观看到变量之间是否存在线性或非线性关系
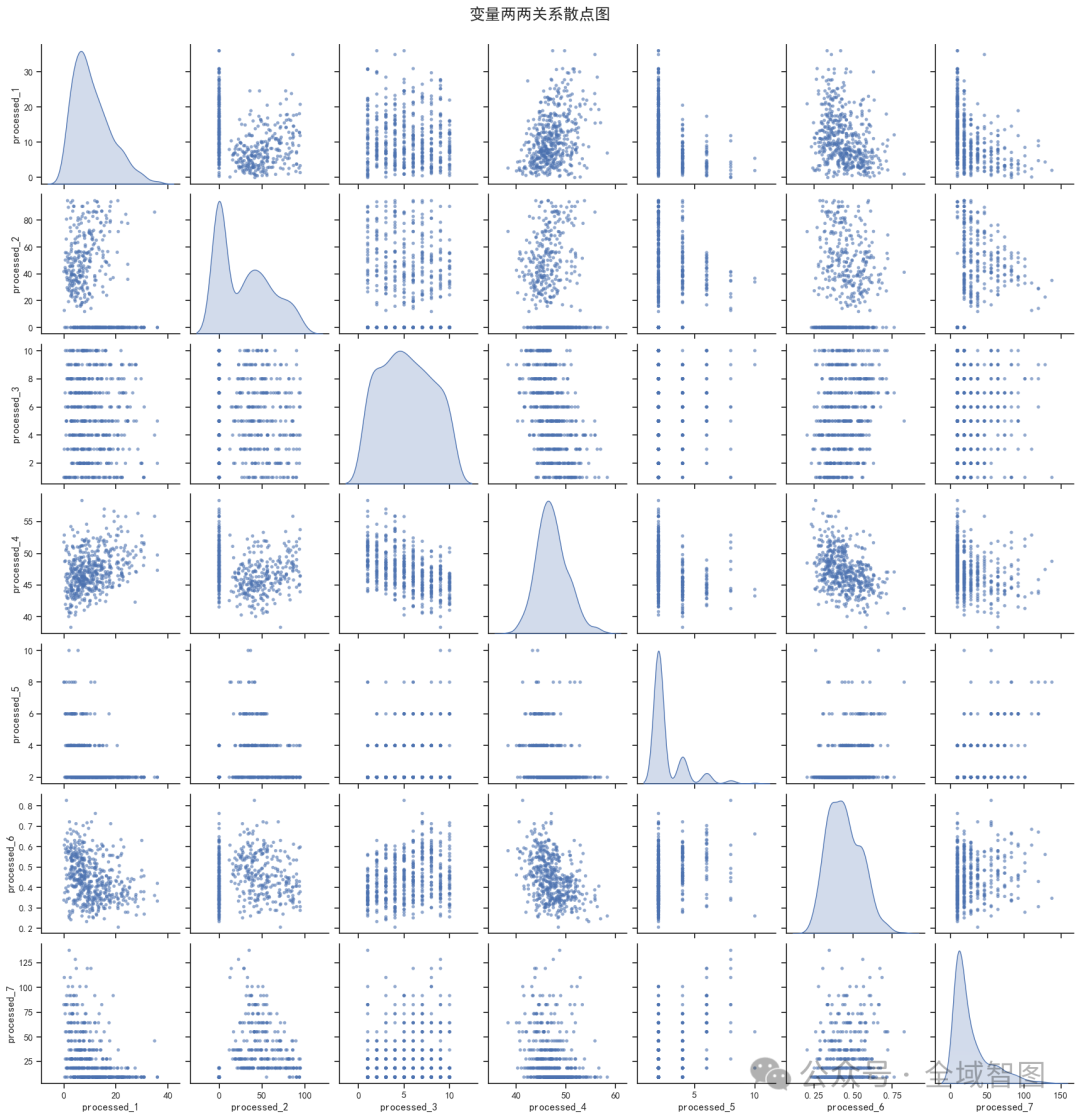
03
模型解释
📈 GAM 偏依赖图 —— 揭示变量的平滑效应及非线性规律;
创建画布
plt.figure(figsize=(15, 12))设置画布大小,保证多子图能排布整齐。
循环绘制每个自变量的偏依赖图
for i, term in enumerate(gam.terms[1:], start=0): # 跳过截距plt.subplot(3, 3, i + 1)XX = gam.generate_X_grid(term=i)
遍历 GAM 模型里的每个自变量(不包括截距),逐个绘制:
generate_X_grid
plt.subplot(3, 3, i+1)
偏依赖与置信区间
pdep, confi = gam.partial_dependence(term=i, X=XX, width=0.95)绘图
plt.plot(XX[:, i], pdep, label="Partial Dependence")plt.fill_between(XX[:, i], confi[:, 0], confi[:, 1],color="r", alpha=0.2, label="95% CI")
在每个子图里:
蓝线(默认) = 平均效应曲线
红色阴影 = 95% 置信区间,直观展示预测的不确定性范围
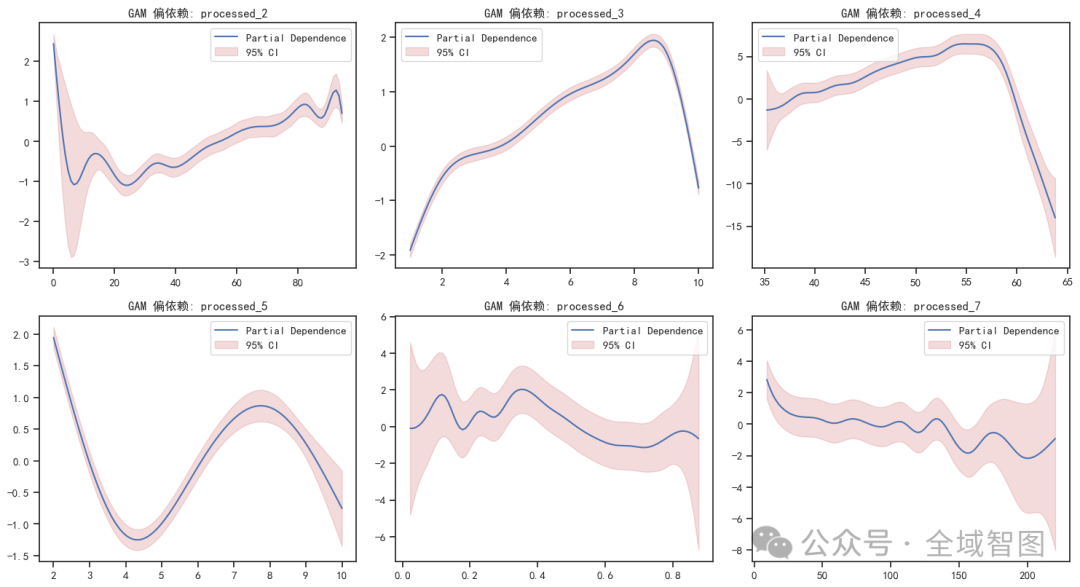
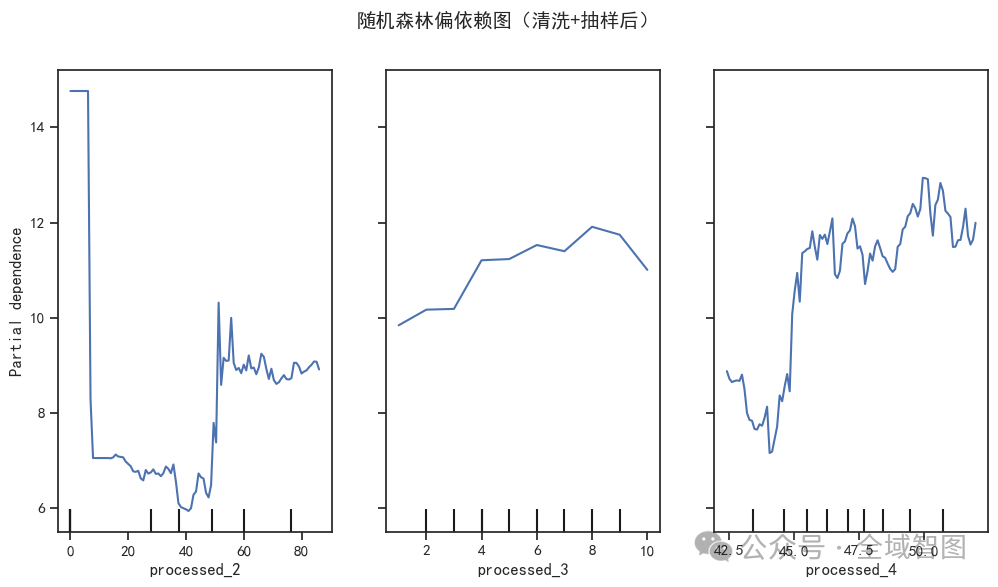
🌲 随机森林偏依赖图 —— 捕捉复杂交互关系,提供更直观的解释力。
数据清理
mask = np.isfinite(X).all(axis=1) & np.isfinite(y)X_clean = X[mask]y_clean = y[mask]
去掉常数列
stds = X_clean.std(axis=0)valid_features = np.where(stds > 1e-8)[0]
过滤掉几乎没变化的特征(方差接近 0 的列),避免模型里出现“无意义变量”。
抽样
n_samples = 1000if X_clean.shape[0] > n_samples:X_sub, y_sub = resample(X_clean, y_clean, n_samples=n_samples, random_state=42)else:X_sub, y_sub = X_clean, y_clean
如果数据太大,随机抽取 1000 个样本做分析,节省计算时间。否则直接用全部数据。
随机森林训练
rf_sub = RandomForestRegressor(n_estimators=200, random_state=42, n_jobs=-1)rf_sub.fit(X_sub, y_sub)
训练一个 200 棵树的随机森林回归模型,用于拟合变量和目标的关系。
偏依赖图 (Partial Dependence Plot)
n_features = min(3, len(X_cols_clean))PartialDependenceDisplay.from_estimator(rf_sub, X_sub, features=list(range(n_features)),feature_names=X_cols_clean, ax=ax)
自动绘制前 3 个变量的 偏依赖图:
横轴 = 自变量取值
纵轴 = 模型预测的平均响应
图形直观展示了该变量与目标变量之间的非线性关系
04
结果评估
自动打印模型精度指标,让科研结果更可复现、更严谨。
从数据清理、变量解释到精度评估,全流程一键化运行,再也不用手动调试零散代码。科研效率飞升 🚀
=== GAM精度 ===R²: 0.9353 Pseudo R²: 0.6663 MSE: 4.2641RMSE: 2.0650===
===随机森林精度 ===R²: 0.9698 MSE: 1.2571RMSE: 1.1212
