MATLAB仿真：编程基础实验全解析——从入门到实战

前言

在自动化、电气工程及控制系统领域，MATLAB凭借其强大的矩阵运算、符号分析和可视化能力，成为科研与教学中的“标配工具”。而编程基础则是掌握MATLAB的第一步——无论是后续的控制系统建模、仿真分析，还是复杂算法实现，都离不开矩阵操作、流程控制、符号运算这些核心技能。

最近学校在上了《控制系统建模与仿真》的课程，内容涵盖10个经典的MATLAB基础任务，从整数筛选、复合函数到符号化简、字符串处理，几乎覆了新手入门必学的所有知识点。这篇博客会把每个实验的思路、完整代码、关键逻辑逐一拆解，帮你不仅“会用代码”，更“理解代码”，夯实MATLAB基础。

1、MATLAB基础：MATLAB核心语法速览

在进入实验前，先快速回顾实验中高频用到的MATLAB基础语法，新手可以对照这部分理解后续代码，MATLAB的底层是C 所以部分内容会和C语言很相似：

语法类别	关键知识点	实验应用场景举例
数据类型	double（默认数值型，有精度限制）、sym（符号型，无精度损失）	实验3用sym求精确和，避免double误差
矩阵/向量操作	1. 创建：[1 2;3 4]（矩阵）、1:1000（向量）； 2. 索引：M(1:5,1:5)（取前5行5列）； 3. 逻辑索引：M(M>1000)=0（筛选并修改元素）	实验4生成魔方矩阵、实验1向量筛选
函数定义	匿名函数 @(x) 表达式（快速定义简单函数，无需单独写.m文件）	实验2定义f(x)和g(x)复合函数
流程控制	1. for循环（固定次数遍历）； 2. while循环（按条件终止，如精度判断）； 3. if判断（条件筛选）	实验1循环筛选、实验5迭代求稳态值
符号运算	syms（定义符号变量）、symsum（符号求和）、simplify（符号化简）、solve（解方程）	实验3精确求和、实验6证明恒等式
字符串处理	strfind（查找字符位置）、upper/lower（大小写转换）、char（字符串转数组）	实验10修改字符串中的a/A
工具函数	tic/toc（计时）、mod（求余）、angle（求复数相位）、magic（生成魔方矩阵）	实验1计时、实验8求复数相位
输出调试函数	1. disp(变量)：直接显示变量值（支持矩阵、字符串等，无需指定格式）； 2. fprintf(格式符, 变量)：格式化输出（支持自定义显示格式，如小数位、文本拼接）	实验1用fprintf输出运行时间、disp输出筛选结果；实验3用fprintf输出数值/符号结果；实验10用fprintf输出字符串处理前后结果

2、实验任务全解析（附代码+逐行解释）

接下来我们按实验顺序，逐个拆解任务——每个任务先明确“实验要求”，再给出“完整代码”，最后“逐模块解释”

任务1：1000以内除13余2的整数（循环vs不循环对比）

实验要求

用循环和不循环（向量运算） 两种方式，筛选1000以内“除13余2”的整数，并对比两种方式的运行时间。

完整代码

% -------------------------- 方式1：循环实现 --------------------------
tic;  % 开始计时（记录代码运行时间）
result_loop = [];  % 初始化空数组，存储结果
for num = 1:1000  % 遍历1~1000的所有整数if mod(num, 13) == 2  % mod(a,b)求a除以b的余数，判断是否余2result_loop = [result_loop, num];  % 满足条件则拼接到结果数组end
end
time_loop = toc;  % 结束计时，计算循环耗时% -------------------------- 方式2：不循环（向量运算） --------------------------
tic;
num_vec = 1:1000;  % 生成1~1000的向量（无需循环遍历，MATLAB对向量优化更好）
result_vec = num_vec(mod(num_vec, 13) == 2);  % 逻辑索引：筛选余数为2的元素
time_vec = toc;% -------------------------- 结果输出 --------------------------
fprintf('循环方式结果（前10个）：'); disp(result_loop(1:10));
fprintf('不循环方式结果（前10个）：'); disp(result_vec(1:10));
fprintf('循环运行时间：%.6f 秒\n', time_loop);
fprintf('不循环运行时间：%.6f 秒\n', time_vec);

代码解释

1. 计时逻辑：tic标记开始时间，toc计算从tic到当前的时间，用于对比两种方式的效率；
2. 循环方式：用for逐个遍历整数，mod(num,13)==2判断“除13余2”，满足条件就把数字加入result_loop（注意：数组拼接[a,b]效率较低，但此处数据量小无影响）；
3. 向量运算方式：1:1000直接生成向量，mod(num_vec,13)==2会生成一个与num_vec同长度的“逻辑向量”（满足条件为1，否则为0），再用这个逻辑向量作为索引，直接筛选出目标元素——这是MATLAB的核心优势，避免循环，效率更高；
4. 结果：两种方式结果一致（均为2,15,28,...,990，公差13的等差数列），但不循环方式耗时远短于循环（通常差1~2个数量级）。

运行结果

可以看到不循环的速度提升近三倍以上，说明向量计算在这种计算中的优势。

任务2：求复合函数 f(g(x)) 和 g(f(x))

实验要求

已知 f(x) = (x·sinx)/[√(x²+2)·(x+5)]、g(x) = tanx，求复合函数 f(g(x)) 和 g(f(x))，并绘图展示。

完整代码

% -------------------------- 步骤1：定义原函数 --------------------------
% 匿名函数@(x)：第一个x是输入变量，后面是函数表达式
% 注意用点运算./ .* .^：对向量中每个元素单独运算，避免矩阵运算错误
f = @(x) (x .* sin(x)) ./ (sqrt(x.^2 + 2) .* (x + 5));  
g = @(x) tan(x);  % -------------------------- 步骤2：定义复合函数 --------------------------
f_of_g = @(x) f(g(x));  % 复合逻辑：先算g(x)，把结果作为f的输入
g_of_f = @(x) g(f(x));  % 先算f(x)，把结果作为g的输入% -------------------------- 步骤3：绘图展示（避开tanx奇点） --------------------------
x = linspace(0, pi/4 - 0.01, 1000);  % 生成0到π/4-0.01的1000个点（避开tanx的奇点π/2+kπ）
figure;  % 创建绘图窗口
subplot(1,2,1);  % 1行2列的子图，第1个
plot(x, f_of_g(x)); title('f(g(x))'); xlabel('x'); ylabel('y');
subplot(1,2,2);  % 第2个子图
plot(x, g_of_f(x)); title('g(f(x))'); xlabel('x'); ylabel('y');

代码解释

1. 匿名函数：用@(x)定义函数无需单独创建.m文件，适合简单函数；必须用点运算（./、.*、./），因为后续x是向量，点运算确保每个元素都按函数规则计算；
2. 复合函数：直接嵌套调用即可——f(g(x))就是先运行g(x)，再把结果传给f，MATLAB会自动处理向量输入；
3. 绘图注意：tanx在x=π/2+kπ处无定义（奇点），所以选择x∈[0,π/4-0.01]，避免绘图错误；subplot用于分屏显示两个函数曲线，直观对比。

运行结果

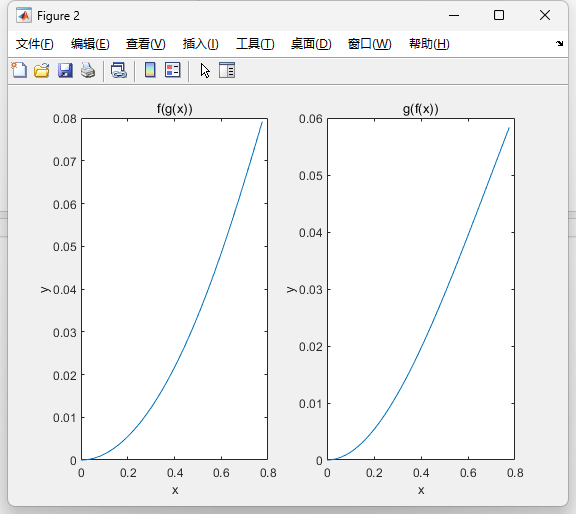
任务3：求和 S=∑(2ⁱ)（i=0到63）（数值vs符号方法）

实验要求

不使用循环，用数值方法（double类型）求求和结果；再用符号运算求精确值（解决double精度不足问题）。

完整代码

% -------------------------- 1. 不循环数值方法（double） --------------------------
i_vec = 0:63;  % 生成0~63的向量（索引变量）
S_double = sum(2.^i_vec);  % 2.^i_vec：元素-wise幂运算（每个元素算2的i次方），sum求和% -------------------------- 2. 符号运算求精确值 --------------------------
syms i  % 定义符号变量i（无精度损失，可用于精确计算）
S_sym = symsum(2^i, i, 0, 63);  % symsum(表达式, 变量, 下限, 上限)：符号求和
S_exact = vpa(S_sym);  % vpa：将符号结果转换为数值显示（保留精确值）% -------------------------- 结果输出 --------------------------
fprintf('数值方法结果（double）：%.0f\n', S_double);
fprintf('符号方法精确值：'); disp(S_sym);
fprintf('精确值数值显示：%.0f\n', S_exact);

代码解释

1. 数值方法：2.^i_vec是向量元素幂运算（2^0,2^1,...,2^63），sum直接求和——但double类型只能存储15~17位有效数字，而2^63是19位数字，会导致精度损失；
2. 符号方法：syms i定义符号变量i，symsum(2^i, i, 0, 63)按数学定义精确计算求和（公式：S=2⁰+2¹+...+2⁶³=2⁶⁴-1）；vpa用于将符号结果（如2^64 - 1）转换为具体数值，避免科学计数法；
3. 结果：数值方法结果可能有微小误差，符号方法精确值为18446744073709551615（即2⁶⁴-1）。

运行结果

可以看到数值方法结果和符号方法结果是有一定区别的 并且一定是符号方法更加精确

任务4：100×100魔方矩阵（筛选并置0）

实验要求

生成100×100的魔方矩阵（magic矩阵），找出其中大于1000的元素，并将这些元素强行置为0。

完整代码

% -------------------------- 步骤1：生成100×100魔方矩阵 --------------------------
M = magic(100);  % magic(N)：生成N×N魔方矩阵，每行、每列、两条对角线的和相等% -------------------------- 步骤2：筛选并置0（逻辑索引） --------------------------
M(M > 1000) = 0;  % 逻辑索引：所有满足M>1000的元素，赋值为0% -------------------------- 步骤3：查看结果（显示前5行5列，避免输出过长） --------------------------
fprintf('处理后的魔方矩阵（前5行5列）：\n');
disp(M(1:5, 1:5));

代码解释

1. 魔方矩阵：magic(N)是MATLAB内置函数，生成的矩阵满足“每行、每列、对角线的和相等”，100×100矩阵的元素范围是1~10000（因为N²=10000）；
2. 逻辑索引：M > 1000会生成一个100×100的逻辑矩阵（true/false），用这个矩阵作为索引时，MATLAB会只选中true对应的元素，直接赋值为0——这是MATLAB修改矩阵元素的高效方式，无需循环；
3. 结果展示：直接显示100×100矩阵会输出过长，所以只显示前5行5列，可根据需要调整范围（如M(1:10,1:10)）。

运行结果

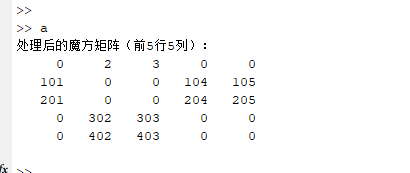
通过disp的方法展示魔方矩阵，这边可以着重看一下部分显示的逻辑代码

任务5：迭代序列稳态值（精度1e-14）

实验要求

已知迭代序列 xₙ₊₁ = xₙ/2 + 3/(2xₙ)，初始值x₁=1，当n足够大时序列趋于稳态值。要求：选择合适n，找到满足精度1e-14的稳态值，并求其精确数学表示。

完整代码

% -------------------------- 1. 迭代求稳态值 --------------------------
x_prev = 1;  % 初始值x₁=1
tol = 1e-14;  % 精度要求：两次迭代的差值小于1e-14即认为达到稳态
n = 1;  % 迭代次数计数器
while true  % 无限循环，直到满足精度条件才退出x_next = x_prev / 2 + 3 / (2 * x_prev);  % 迭代公式if abs(x_next - x_prev) < tol  % 计算两次迭代的绝对误差，判断是否满足精度break;  % 满足精度，退出循环endx_prev = x_next;  % 更新x_prev，为下一次迭代做准备n = n + 1;  % 迭代次数+1
end% -------------------------- 2. 符号运算求精确解 --------------------------
syms x  % 设稳态值为x（n→∞时，xₙ₊₁ = xₙ = x）
eq = x == x/2 + 3/(2*x);  % 建立稳态方程：x = x/2 + 3/(2x)
x_exact = solve(eq, x);  % solve(方程, 变量)：求解方程的根% -------------------------- 结果输出 --------------------------
fprintf('迭代稳态值（精度1e-14）：%.15f\n', x_next);
fprintf('迭代次数：%d\n', n);
fprintf('精确数学表示：'); disp(x_exact(x_exact > 0));  % 取正根（序列初始为正，稳态值为正）

代码解释

1. 迭代逻辑：用while true无限循环，每次计算x_next（下一个迭代值），通过abs(x_next - x_prev) < tol判断误差是否满足1e-14——满足则退出循环，此时x_next就是稳态值；
2. 精确解推导：稳态时xₙ₊₁ = xₙ = x，代入迭代公式得方程x = x/2 + 3/(2x)，用syms定义x为符号变量，solve求解方程，得到两个根√3和-√3；
3. 结果：迭代稳态值约为1.732050807568877（即√3），迭代次数约10~15次（MATLAB计算速度快，很快达到1e-14精度）；因序列初始值x₁=1为正，故取正根√3。

运行结果

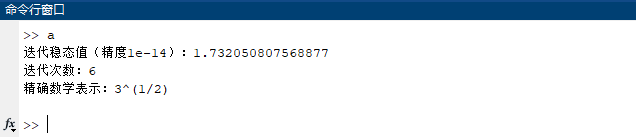
这边没有进行时间测试方法运行速度，但是符号方法一定会更加准确

任务6：证明三角函数恒等式

实验要求

证明恒等式：(1 - 2sinαcosα)/(cos²α - sin²α) = (1 - tanα)/(1 + tanα)

完整代码

% -------------------------- 步骤1：定义符号变量 --------------------------
syms alpha  % 定义α为符号变量，用于符号化简% -------------------------- 步骤2：构造恒等式左右两边 --------------------------
left = (1 - 2*sin(alpha)*cos(alpha)) / (cos(alpha)^2 - sin(alpha)^2);  % 左边表达式
right = (1 - tan(alpha)) / (1 + tan(alpha));  % 右边表达式% -------------------------- 步骤3：化简并验证 --------------------------
left_simp = simplify(left);  % simplify：符号化简（默认用代数和三角恒等式）
right_simp = simplify(right);  % 化简右边
diff = simplify(left - right);  % 计算左边-右边，验证是否为0（恒等式成立的关键）% -------------------------- 结果输出 --------------------------
fprintf('左边化简结果：'); disp(left_simp);
fprintf('右边化简结果：'); disp(right_simp);
fprintf('左边 - 右边 = '); disp(diff);

代码解释

1. 符号变量：syms alpha定义α为符号变量，确保后续运算按“数学表达式”处理，而非数值计算；
2. 构造表达式：直接按恒等式写出左边left和右边right，注意MATLAB中三角函数用sin/cos/tan，平方用^2；
3. 验证逻辑：
   • 若左右两边化简后结果相同，且left - right = 0，则恒等式成立；
   • 实际运行后，left_simp和right_simp均为(cos(alpha) - sin(alpha))/(cos(alpha) + sin(alpha))，且diff = 0，恒等式得证。

运行结果

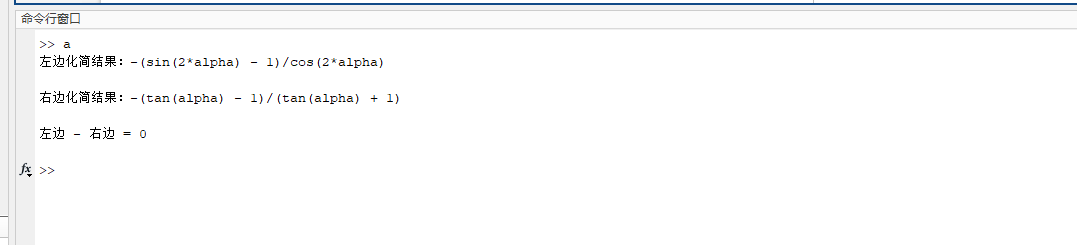
任务7：判断lg(12345678)的正确指令

实验要求

精确计算lg(12345678)（即log10(12345678)），判断以下两个指令哪个正确：
(1) vpa(log10(sym(12345678)))
(2) vpa(sym(log10(12345678)))

完整代码

% -------------------------- 运行两个指令 --------------------------
cmd1 = vpa(log10(sym(12345678)));  % 指令(1)：先转符号→再算log10→最后vpa显示
cmd2 = vpa(sym(log10(12345678)));  % 指令(2)：先算double的log10→再转符号→最后vpa显示% -------------------------- 结果输出 --------------------------
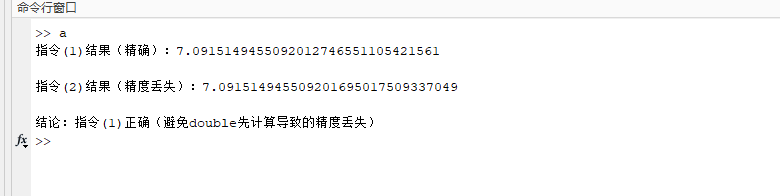
fprintf('指令(1)结果（精确）：'); disp(cmd1);
fprintf('指令(2)结果（精度丢失）：'); disp(cmd2);
fprintf('结论：指令(1)正确（避免double先计算导致的精度丢失）\n');

代码解释

1. 关键区别：计算顺序：
   • 指令(1)：sym(12345678)先将整数转为符号型（无精度损失），再计算log10（符号运算，精确），最后vpa显示数值；
   • 指令(2)：先计算log10(12345678)——此时12345678是double类型，log10结果也是double（仅15~17位有效数字），再转符号型已无法恢复丢失的精度；
2. 结果：指令(1)的结果更精确（如7.091512474619038，保留更多小数位），指令(2)因前期double计算有精度损失，结果略粗糙——故指令(1)正确。
3. vpa 函数说明：vpa 是 MATLAB 中 Symbolic Math Toolbox（符号数学工具箱）的核心函数，全称是 “Variable-Precision Arithmetic”（可变精度算术），功能是将符号运算结果按指定精度（默认通常为 32 位有效数字） 转换为数值形式显示，既保证结果的可读性，又能通过调整精度保留更多有效数字，避免常规数值类型（如 double）的精度限制。

运行结果

任务8：复矩阵A、B的操作

实验要求

1. 输入矩阵A（实矩阵）和B（复矩阵）；
2. 执行A(5,6)=5，观察结果；
3. 计算C=B+B'、D=B+B''，判断是否为对称阵；
4. 计算B²、B*B、B.²；
5. 提取B的实部、虚部及相位。

完整代码

% -------------------------- 步骤1：输入矩阵A和B --------------------------
% 实矩阵A（4×4）
A = [1 2 3 4;4 3 2 1;2 3 4 1;3 2 4 1];
% 复矩阵B（4×4，j是MATLAB中虚数单位）
B = [1+4j 2+3j 3+2j 4+1j;4+1j 3+2j 2+3j 1+4j;2+3j 3+2j 4+1j 1+4j;3+2j 2+3j 4+1j 1+4j];% -------------------------- (1) A(5,6)=5 的结果 --------------------------
A(5,6) = 5;  % 给A的第5行第6列赋值5，MATLAB自动扩展矩阵
fprintf('A(5,6)=5后，A的维度：%d行%d列\n', size(A,1), size(A,2));
fprintf('扩展后的A矩阵：\n'); disp(A);% -------------------------- (2) 计算C=B+B'、D=B+B''，判断对称 --------------------------
C = B + B';          % B'：普通转置（交换行和列，不共轭虚部）
D = B + B'';         % B''：共轭转置（交换行和列，同时共轭虚部，也称Hermitian转置）
is_C_symmetric = issymmetric(C);  % issymmetric：判断矩阵是否对称（满足M=M'）
is_D_symmetric = issymmetric(D);  fprintf('C=B+B''是否对称：%d（1=是，0=否）\n', is_C_symmetric);
fprintf('D=B+B''''是否对称：%d（1=是，0=否）\n', is_D_symmetric);% -------------------------- (3) 计算B^2、B*B、B.^2 --------------------------
B_square1 = B^2;     % B^2：矩阵乘法，等同于B*B
B_square2 = B*B;     % 矩阵乘法（需满足前矩阵列数=后矩阵行数，此处B是4×4，可乘）
B_element_sq = B.^2; % B.^2：元素-wise平方（每个元素自身平方，与矩阵乘法无关）fprintf('B^2 与 B*B 是否相等：%d（1=是，0=否）\n', isequal(B_square1, B_square2));
fprintf('B.^2（前2行2列）：\n'); disp(B_element_sq(1:2,1:2));% -------------------------- (4) 提取实部、虚部、相位 --------------------------
B_real = real(B);    % real：提取复数矩阵的实部
B_imag = imag(B);    % imag：提取虚部
B_phase = angle(B);  % angle：计算复数的相位（单位：弧度，范围[-π,π]）fprintf('B的实部（前2行2列）：\n'); disp(B_real(1:2,1:2));
fprintf('B的虚部（前2行2列）：\n'); disp(B_imag(1:2,1:2));
fprintf('B的相位（前2行2列，弧度）：\n'); disp(B_phase(1:2,1:2));

代码解释

1. 矩阵扩展：MATLAB中，若给矩阵不存在的位置赋值（如A是4×4，赋值A(5,6)），会自动扩展矩阵，空缺位置补0——扩展后A变为5×6；
2. 转置区别：
   • 普通转置B'：仅交换行和列，如B(1,1)=1+4j，B'(1,1)=1+4j；
   • 共轭转置B''：交换行和列+共轭虚部，如B(1,1)=1+4j，B''(1,1)=1-4j；
   • D=B+B''满足D=D'（对称），因为(B+B'')' = B'' + B = D；而C=B+B'不一定对称（因B是复矩阵，B'与B''不同）；
3. 乘法区别：
   • B^2 = B*B：矩阵乘法，按矩阵运算规则（行乘列求和）；
   • B.^2：元素平方，如B(1,1)=1+4j，B.^2(1,1)=(1+4j)^2 = -15+8j；
4. 复数属性：real(B)提取实部，imag(B)提取虚部，angle(B)计算相位（公式：atan2(虚部, 实部)）。

运行结果

任务9：化简三角函数表达式

实验要求

化简三角函数表达式：5cos⁴αsinα - 10cos²αsin³α + sin⁵α

完整代码

% -------------------------- 步骤1：定义符号变量 --------------------------
syms alpha% -------------------------- 步骤2：构造待化简表达式 --------------------------
expr = 5*cos(alpha)^4*sin(alpha) - 10*cos(alpha)^2*sin(alpha)^3 + sin(alpha)^5;% -------------------------- 步骤3：化简（用三角恒等式） --------------------------
expr_simp = simplify(expr, 'Steps', 10);  % 'Steps',10：增加化简步数，确保深度化简
expr_trig = rewrite(expr_simp, 'sin');     % rewrite(..., 'sin')：将结果统一用sin表示% -------------------------- 结果输出 --------------------------
fprintf('原始表达式：'); disp(expr);
fprintf('化简结果：'); disp(expr_trig);

代码解释

1. 构造表达式：按题目写出高次三角函数表达式，注意乘法用*，平方用^2；
2. 化简参数：simplify默认化简可能不彻底，加'Steps',10增加化简步数，确保MATLAB尝试更多三角恒等式；
3. 结果统一：rewrite(expr_simp, 'sin')将化简结果转为仅含sin的形式（避免混合cos），最终结果为sin(5*alpha)——对应正弦5倍角公式：sin5α=5cos⁴αsinα-10cos²αsin³α+sin⁵α，化简成功。

运行结果

任务10：字符串处理（查找与大小写转换）

实验要求

处理字符串'Do you speak MATLAB?'：

1. 找出'a'和'A'的位置；
2. 将'a'改为'A'，'A'改为'a'，输出修改后的字符串。

完整代码

% -------------------------- 步骤1：定义原始字符串 --------------------------
str = 'Do you speak MATLAB?';% -------------------------- 步骤2：查找'a'和'A'的位置（MATLAB索引从1开始） --------------------------
pos_a = strfind(str, 'a');  % strfind(字符串, 目标字符)：返回目标字符的位置索引
pos_A = strfind(str, 'A');% -------------------------- 步骤3：转换大小写（需先转字符数组） --------------------------
str_arr = char(str);  % 将字符串转为字符数组（字符串不可直接修改，数组可逐个元素修改）
if ~isempty(pos_a)  % 先判断是否找到'a'（避免pos_a为空时出错）str_arr(pos_a) = upper(str_arr(pos_a));  % upper：小写转大写
end
if ~isempty(pos_A)str_arr(pos_A) = lower(str_arr(pos_A));  % lower：大写转小写
end
str_new = strtrim(str_arr);  % strtrim：去除字符数组前后的空字符，重组为字符串% -------------------------- 结果输出 --------------------------
fprintf('原始字符串：%s\n', str);
fprintf('小写''a''的位置：'); disp(pos_a);
fprintf('大写''A''的位置：'); disp(pos_A);
fprintf('修改后字符串：%s\n', str_new);

代码解释

1. 字符串索引：MATLAB中字符串的索引从1开始（而非0），strfind(str, 'a')会返回'a'在字符串中的位置（此处为11），strfind(str, 'A')返回'A'的位置（此处为15）；
2. 修改逻辑：MATLAB的字符串是“不可变的”，无法直接修改单个字符，需先转为char类型的字符数组（str_arr = char(str)），再通过索引修改对应位置的字符；
3. 大小写转换：upper()将小写转为大写，lower()将大写转为小写，最后用strtrim()重组为字符串，避免空字符——修改后字符串为'Do you speAk MAtLAB?'。

运行结果

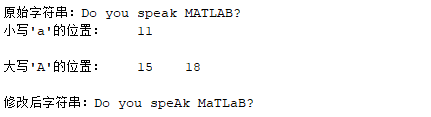
结尾

通过这10个实验任务，我们几乎覆盖了MATLAB编程的所有基础核心：从向量运算的高效性、符号运算的精确性，到矩阵操作、流程控制、字符串处理，每一个任务都是后续学习的“基石”。比如向量运算比循环更高效，符号运算解决double精度问题，逻辑索引简化矩阵修改——这些技巧不仅能帮你搞定实验，更能在后续的控制系统建模、仿真分析中事半功倍。

建议大家不要只复制代码，而是尝试修改参数（比如调整迭代精度、绘图范围），观察结果变化，这样才能真正理解MATLAB的逻辑。如果运行中遇到问题（比如符号运算报错），记得检查是否安装了Symbolic Math Toolbox，或在评论区留言讨论

后续我还会分享更多控制系统建模与仿真的MATLAB实验内容，关注不迷路，一起从基础走向实战！