Stanford CS336 Lecture3 | Architectures, hyperparameters
Stanford CS336 Lecture3 | Architectures, hyperparameters
- 一、 Common architecture variations 常见模型架构变种
- 1、 前置归一化vs后置归一化(Pre-vs-post norm)
- 2、 LayerNorm vs RMSNorm
- 3、 activations激活函数
- ReLU函数
- GeLU函数
- Gated 函数及其变种 *GLU
- ReGLU
- GeGLU
- SwishGLU
- 4、 rotary position embedding
- Absoulte embeddings
- ROPE
- 二、 Hyperparameters that (do or don’t) matter 超参数相关问题
- 三、 正则化
- 四、 稳定训练过程的 trick
- 五、 注意力机制
一、 Common architecture variations 常见模型架构变种
1、 前置归一化vs后置归一化(Pre-vs-post norm)
先看一下基本的不带归一化的最基本的残差连接最左侧图1是不带归一化的残差连接,输入x复制一份,其中一个x通过f得到f(x)后与x进行相加。
y = f ( x ) + x y = f(x) + x y=f(x)+x
后置归一化如图2,前面的数据流和图一中一致,当做完add后,对得到的和在进行Normalization,transformer原论文中使用的就是这种Normalization方式
y = N o r m ( f ( x ) + x ) y = Norm(f(x) + x) y=Norm(f(x)+x)
前置归一化如图3,x复制为两份,一份进入Norm层进行归一化然后再进入f层,得到的一个与第一份x进行add,最后输出y。这目前LLM最常使用的Normlization方式
y = f ( N o r m ( x ) ) + x y = f(Norm(x)) + x y=f(Norm(x))+x
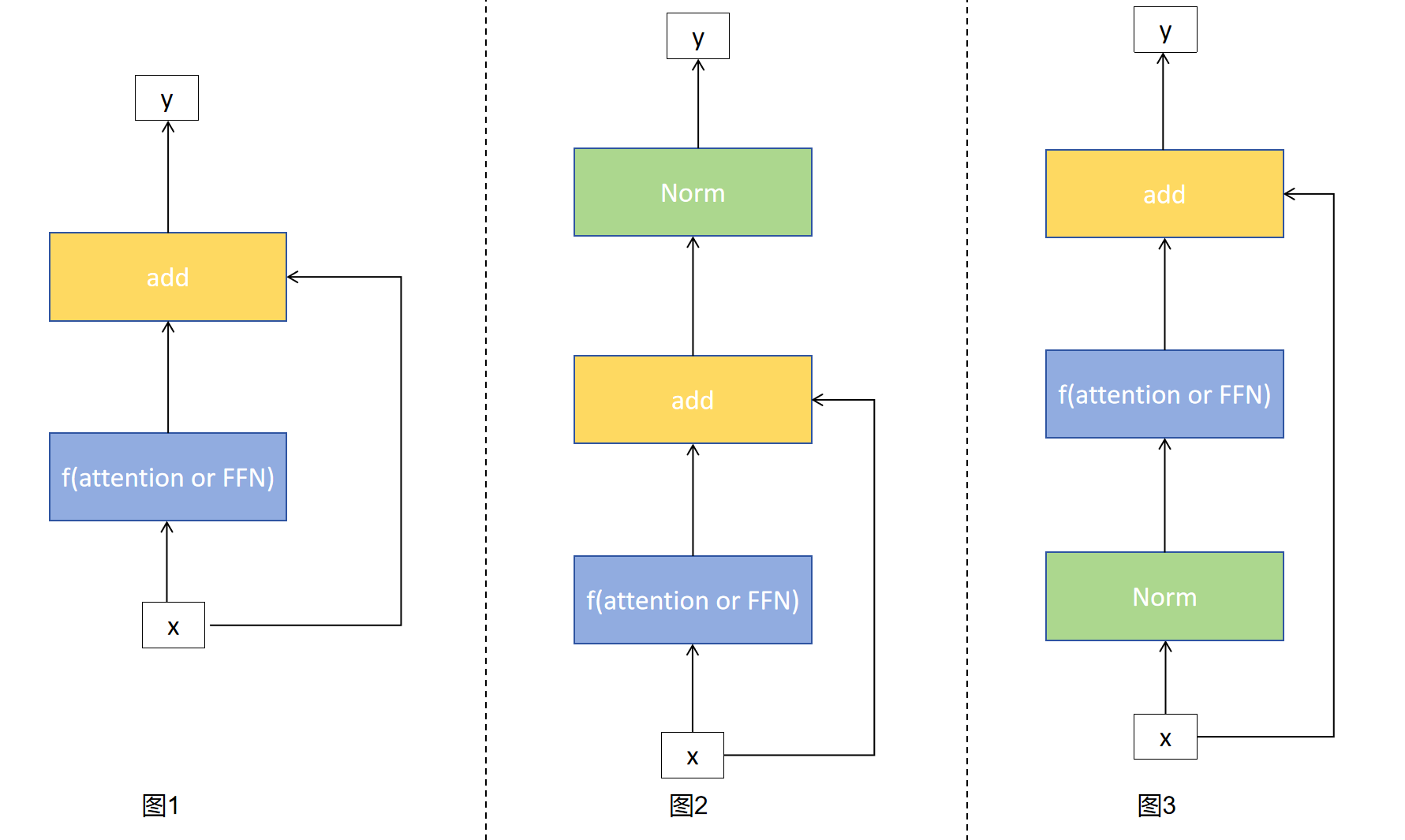
pre-vs-post norm
| 对比项 | Pre-Norm | Post-Norm |
|---|---|---|
| LayerNorm 位置 | 在残差连接(Residual)之前 | 在残差连接(Residual)之后 |
| 稳定性 | 更容易训练,稳定性高 | 容易梯度爆炸/消失 |
| 表现(收敛) | 初期收敛快,稳定但上限略低 | 初期慢但最终性能可能略高 |
| 使用场景 | 更适合深层 Transformer | 早期 Transformer (如原始论文) |
| 常见模型 | GPT-2、BERT、T5、ViT(大多使用 Pre) | 原始 Transformer(Vaswani et al., 2017) |
为什么pre-norm更加稳定,原因在于残差连接的本质是恒等映射,pre-norm并没有破坏这种恒等映射 y = f ( N o r m ( x ) ) + x y = f(Norm(x)) + x y=f(Norm(x))+x,而post-norm则是破坏了这种恒等映射 y = N o r m ( f ( x ) + x ) y = Norm(f(x) + x) y=Norm(f(x)+x)
2、 LayerNorm vs RMSNorm
RMSNorm和LayerNorm的最主要区别就是RMSNorm只归一化方差,不处理均值,同时没有偏置。
对于LayerNorm:
L a y e r N o r m ( x ) = x − μ 1 d ∑ i = 1 d ( x i − μ ) 2 + ϵ . γ + β LayerNorm(x) = \frac{x-\mu}{\sqrt{\frac{1}{d}\sum_{i=1}^{d}(x_i-\mu)^2+\epsilon}} . \gamma +\beta LayerNorm(x)=d1∑i=1d(xi−μ)2+ϵx−μ.γ+β
R M S N o r m ( x ) = x 1 d ∑ i = 1 d ( x i ) 2 + ϵ . γ RMSNorm(x) = \frac{x}{\sqrt{\frac{1}{d}\sum_{i=1}^{d}(x_i)^2+\epsilon}} . \gamma RMSNorm(x)=d1∑i=1d(xi)2+ϵx.γ
| 特性 | LayerNorm | RMSNorm |
|---|---|---|
| 是否减均值 | 是 | 否 |
| 归一化基础 | x − μ δ \frac{x-\mu}{\delta} δx−μ | x R M S ( x ) \frac{x}{RMS(x)} RMS(x)x |
| 可学习参数 | β 、 γ \beta 、\gamma β、γ | γ \gamma γ |
| 计算复杂度 | 较高(需算均值) | 更低(少一次减法和均值) |
| 数值稳定性 | 高(中心化 + 归一化) | 高(但依赖输入对称性) |
| 训练速度 | 稍慢 | 稍快(尤其在大模型中) |
| 内存/计算成本 | 高 | 更低 |
使用RMSNorm是会有更少的参数移动。
3、 activations激活函数
ReLU函数
ReLU函数是最早的激活函数:
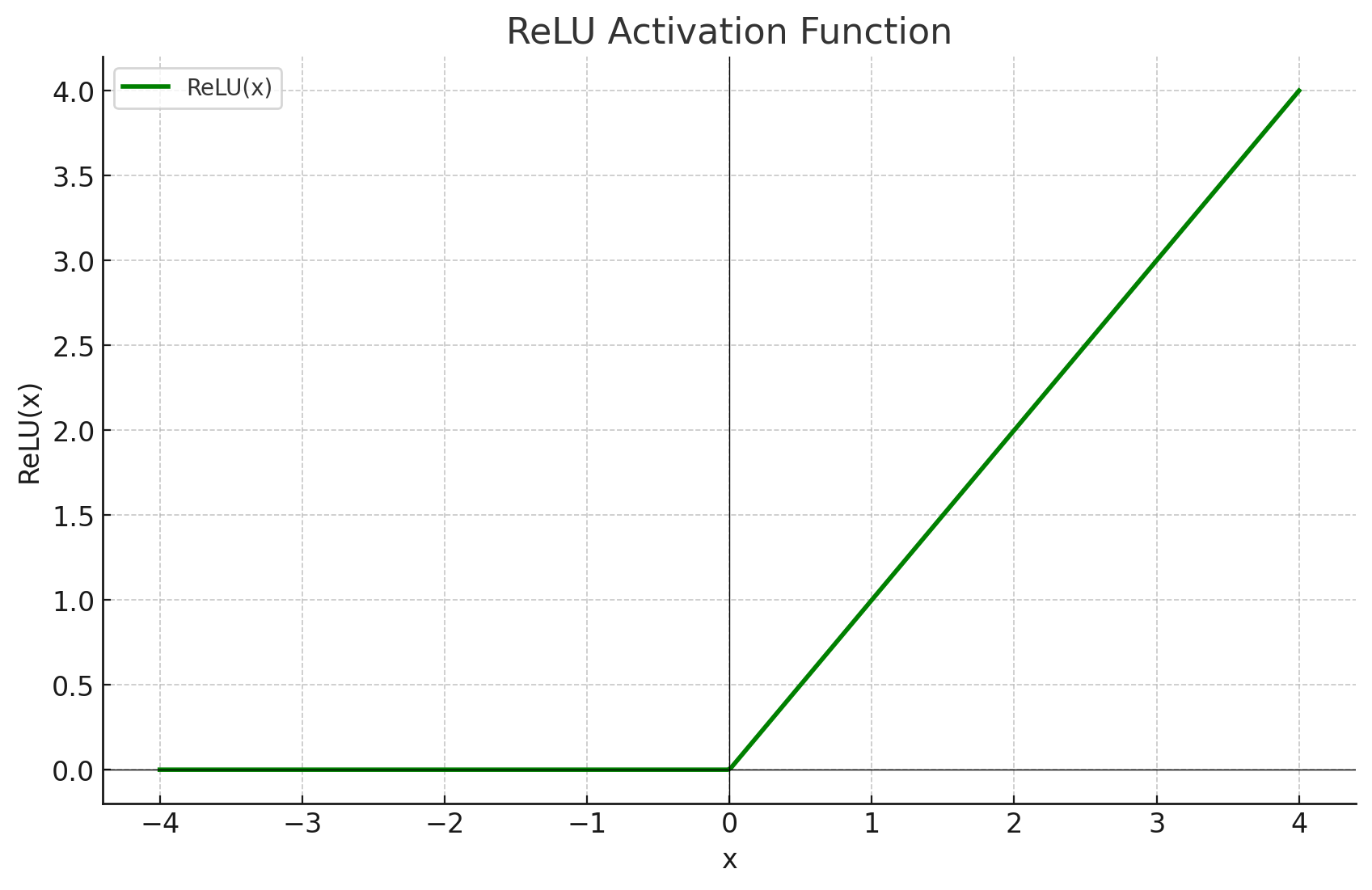
R e L U ( x ) = m a x ( 0 , x W 1 ) ReLU(x)=max(0, xW_1) ReLU(x)=max(0,xW1)
GeLU函数
GeLU(Gaussion Error Linear Uint)
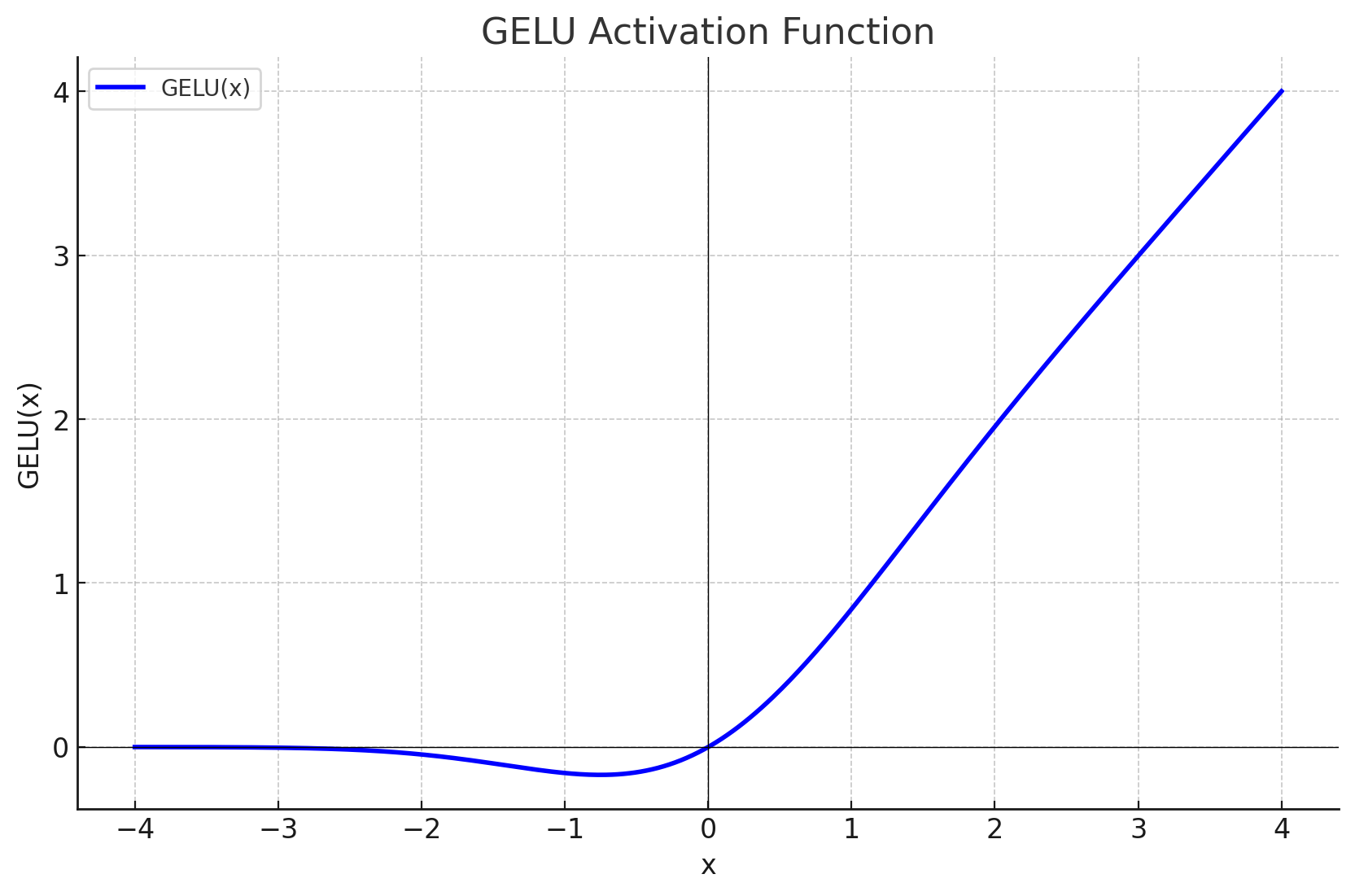
GeLU并不像ReLU那样简单地截断负数,而是以概率的方式决定保留多少输入。
G E L U ( x ) = x ⋅ Φ ( x ) GELU(x)=x⋅Φ(x) GELU(x)=x⋅Φ(x)
其中,Φ(x)是正态分布的累计分布函数
Φ ( x ) = 1 2 π ∫ − ∞ x e − t 2 2 d t Φ(x) = \frac{1}{\sqrt{2\pi}}\int^x_{- \infty}e^{\frac{-t^2}{2}}dt Φ(x)=2π1∫−∞xe2−t2dt
Φ ( x ) ≈ 1 2 [ 1 + e r f ( x 2 ) ] Φ(x) \approx \frac{1}{2}[1+erf(\frac{x}{\sqrt{2}})] Φ(x)≈21[1+erf(2x)]
上面的公式中erf是误差函数,由于其和正态分布的累计分布函数高度相似于是可以用erf去近似CDF
e r f ( x ) = 2 π ∫ 0 x e − t 2 d t erf(x) = \frac{2}{\sqrt{\pi}}\int^x_0e^{-t^2}dt erf(x)=π2∫0xe−t2dt
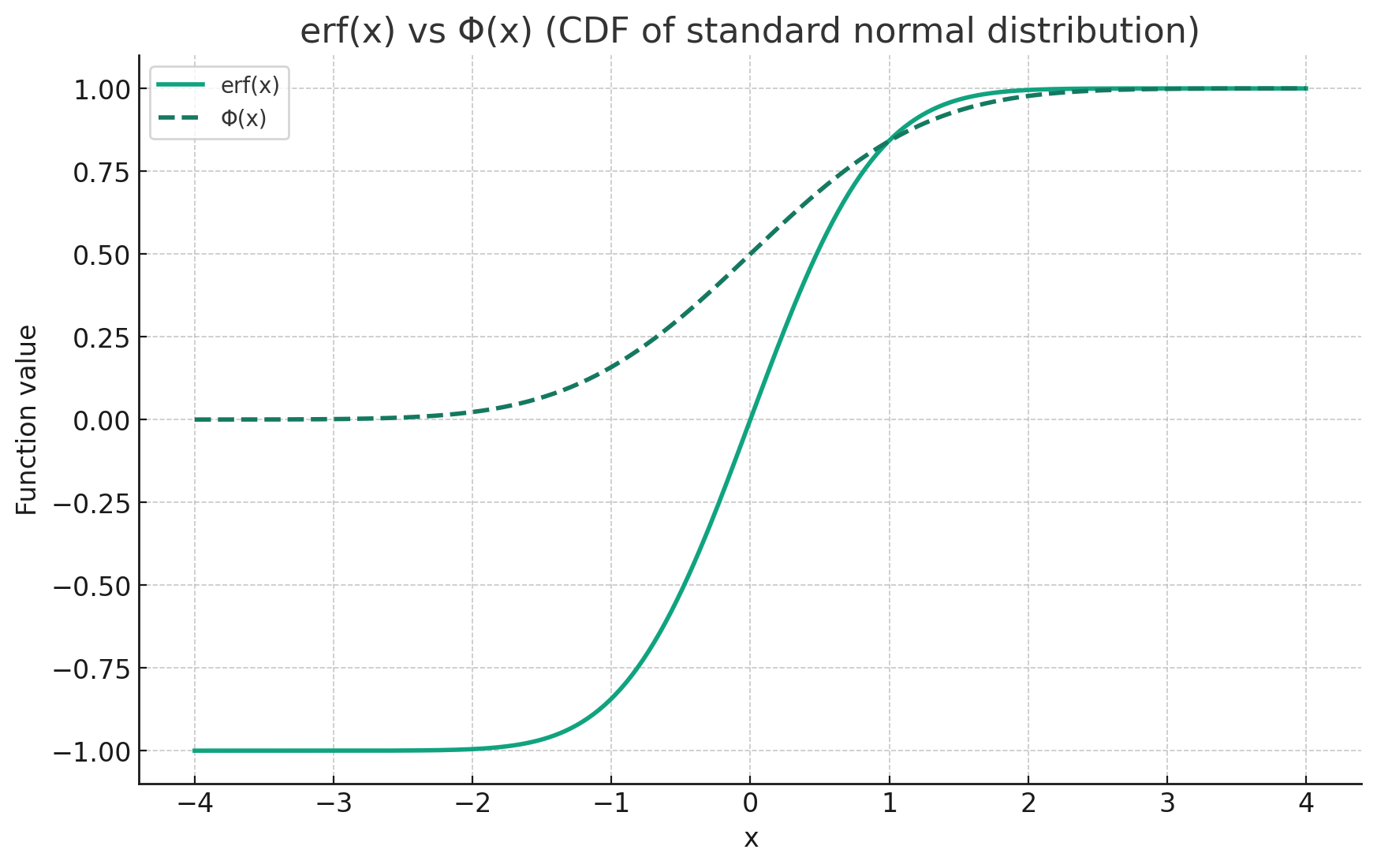
对于GeLU更加直观的理解是:
当 𝑥≪0,GELU(x) ≈ 0
当 𝑥≈0,GELU(x) ≈ 0.5 * x
当 𝑥≫0,GELU(x) ≈ x
相较于ReLU而言,GeLU更加平滑,在x=0处依然可导可微,不会突然被硬切断。
在pytorch底层采用了一种更加快速的方式计算CDF,(erf函数涉及积分操作,并且没有初等函数解析解,计算起来需要用数值计算的方法,还是比较慢)
G E L U ( x ) ≈ 0.5 x [ 1 + tanh ( π 2 ( x + 0.044715 x 3 ) ) ] \mathrm{GELU}(x) \approx 0.5x \left[1 + \tanh\left( \sqrt{\frac{\pi}{2}} \left( x + 0.044715 x^3 \right) \right) \right] GELU(x)≈0.5x[1+tanh(2π(x+0.044715x3))]
Gated 函数及其变种 *GLU
Gated Linear Uint是将输入看作两部分,使其中一部分作为门控信号太调整另一部分的信息流。GLU会引入一个新的参数。
ReGLU
对于RELU而言其输出应该是:
m a x ( 0 , x W 1 ) max(0, xW_1) max(0,xW1)
而这里引入门控
m a x ( 0 , x W 1 ) ⊗ ( x V ) max(0, xW_1) \otimes(xV) max(0,xW1)⊗(xV)
前面的ReLU负责门控,后面引入V负责控制信息流入多少。
GeGLU
GeGLU就是GeLU+Gated
G e L U ( x W ) ⊗ ( x V ) GeLU(xW) \otimes(xV) GeLU(xW)⊗(xV)
SwishGLU
S w i s h ( x W ) ⊗ ( x V ) Swish(xW) \otimes(xV) Swish(xW)⊗(xV)
4、 rotary position embedding
Absoulte embeddings
最初的transfomer原论文使用的是sine embeddings也就是sinusoidal positional encoding:
E m b e d ( x , i ) = v x + p i Embed(x, i)=v_x+p_i Embed(x,i)=vx+pi
- v x v_x vx是token x的词向量
- p i p_i pi是i位置处对应的位置向量
这种位置编码就是绝对位置编码(abslute embeddings)。
P E ( p o s , 2 i ) = s i n ( p o s 100 0 2 i d m o d e l ) PE(pos, 2i)=sin(\frac{pos}{1000^{\frac{2i}{d_{model}}}}) PE(pos,2i)=sin(1000dmodel2ipos)
P E ( p o s , 2 i + 1 ) = c o s ( p o s 100 0 2 i d m o d e l ) PE(pos, 2i+1)=cos(\frac{pos}{1000^{\frac{2i}{d_{model}}}}) PE(pos,2i+1)=cos(1000dmodel2ipos)
-
pos:当前 token 的位置索引(0, 1, 2, …)
-
i:当前维度对的索引(从 0 到 𝑑 m o d e l / 2 − 1 𝑑_{model} / 2 -1 dmodel/2−1
-
𝑑 m o d e l 𝑑_{model} dmodel :embedding 向量总维度
向量的偶数维使用 sin,奇数维使用 cos,这样每个位置向量都是 [sin, cos, sin, cos, …] 的形式。
ROPE
相对位置编码不关注词的绝对位置信息,而是关注相对位置信息,因为绝对位置信息的用处实际上并不是很大。
relative embedding应该具有如下特征,假设token x在sequence中的位置为i,其relative embedding表示为 f ( x , i ) f(x,i) f(x,i),token y在sequence中的位置为j,表示为 f ( y , j ) f(y,j) f(y,j)
两者之间的内积应该只和x,y以及i-j有关即
< f ( x , i ) , f ( y , j ) > = g ( x , y , i − j ) <f(x,i),f(y,j)>=g(x, y, i - j) <f(x,i),f(y,j)>=g(x,y,i−j)
怎样才能做到relative embedding的内积和绝对位置无关,而只和相对位置有关,这里就有向量旋转的关键性质:
两个vector旋转相同的角度其内积不变,其内积之与两者之间的夹角有关
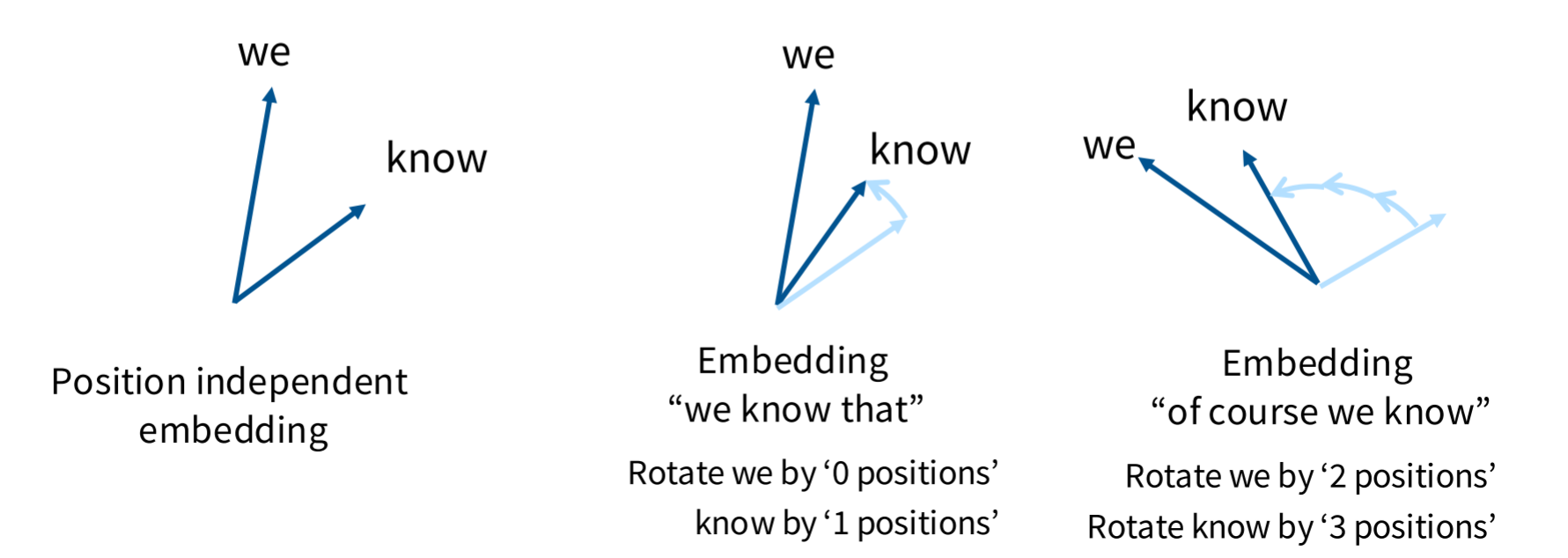
这样通过旋转embedding,既可以给embedding加上位置信息,同时也满足了相对位置这一条件。
对于二维向量的旋转是容易做到的,就是将向量乘上一个旋转矩阵即可完成旋转向量这一操作。
[ c o s θ − s i n θ s i n θ c o s θ ] \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix} [cosθsinθ−sinθcosθ]
然后将多个这样的矩阵拼接起来就有了旋转矩阵
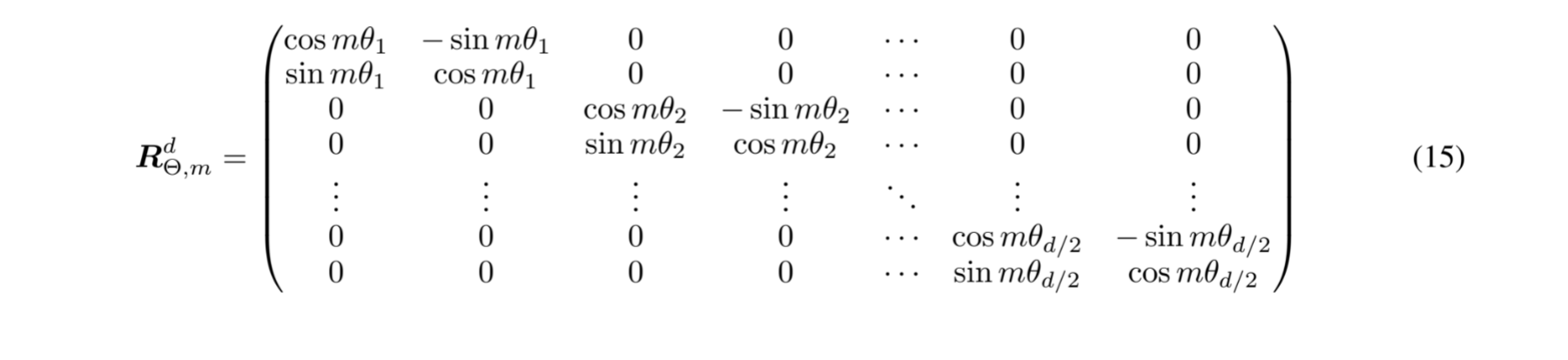
下面是llama中的实现

二、 Hyperparameters that (do or don’t) matter 超参数相关问题
d m o d e l 和 d f f d_{model}和d_{ff} dmodel和dff
FFN的 d m o d e l d_{model} dmodel和 d f f d_{ff} dff的大小一般是一个倍数关系.
d f f = 4 d m o d e l d_{ff}=4d_{model} dff=4dmodel
一般隐藏层维度和嵌入维度是一个4倍关系,这是transformer原论文中一致延用过来的,大部分模型都采用的这个关系,一般认为放大4倍能让模型在中间层学习到更复杂的特征。
这个数量关系并非绝对的,也有很多模型并不采用这个比例:
例如采用了GLU的变体FFN就是个例外:
d f f = 8 3 d m o d e l d_{ff}=\frac{8}{3}d_{model} dff=38dmodel
因为这样可以保证和标准FFN参数量不变。
标准FFN:
F F N ( x ) = W 2 ( a c t i v a t i o n ( W 1 x ) ) FFN(x) = W_2 (activation(W_1x)) FFN(x)=W2(activation(W1x))
其参数量为:
d m o d e l × d f f + d f f × d m o d e l = 2 d m o d e l × d f f d_{model} \times d_{ff} + d_{ff} \times d_{model} = 2d_{model} \times d_{ff} dmodel×dff+dff×dmodel=2dmodel×dff
对于变体的加入GLU的FFN
F F N G L U ( x ) = W 3 ( ( W 1 x ) ⊗ a c t i v a t i o n ( W 2 x ) ) FFN_GLU(x) = W_3((W_1x) \otimes activation(W_2x)) FFNGLU(x)=W3((W1x)⊗activation(W2x))
这里的模型参数为 W 1 、 W 2 、 W 3 W_1、W_2、W_3 W1、W2、W3
3 d m o d e l d f f 3d_{model}d_{ff} 3dmodeldff
所以啊如果要想变体后的FFN和原来的FFN相同,这就需要 d f f = 8 3 d m o d e l d_{ff}=\frac{8}{3}d_{model} dff=38dmodel。
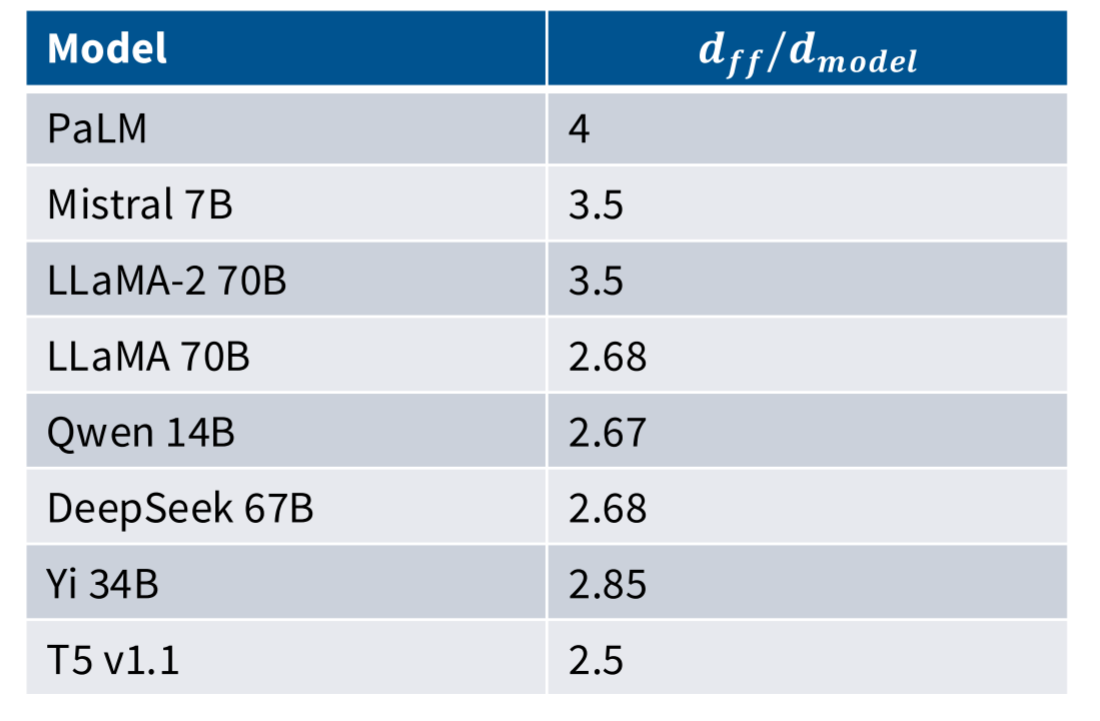
这里还有另一个例外就是T5模型。其将FFN的 d f f d_{ff} dff放大了将近64倍
d m o d e l = 1024 d_{model}=1024 dmodel=1024
d f f = 65536 d_{ff}=65536 dff=65536
这里有论文做过相关研究,关于这个ratio和损失函数损失值的关系,可以看到最优的结果应该是存在于1-10之间
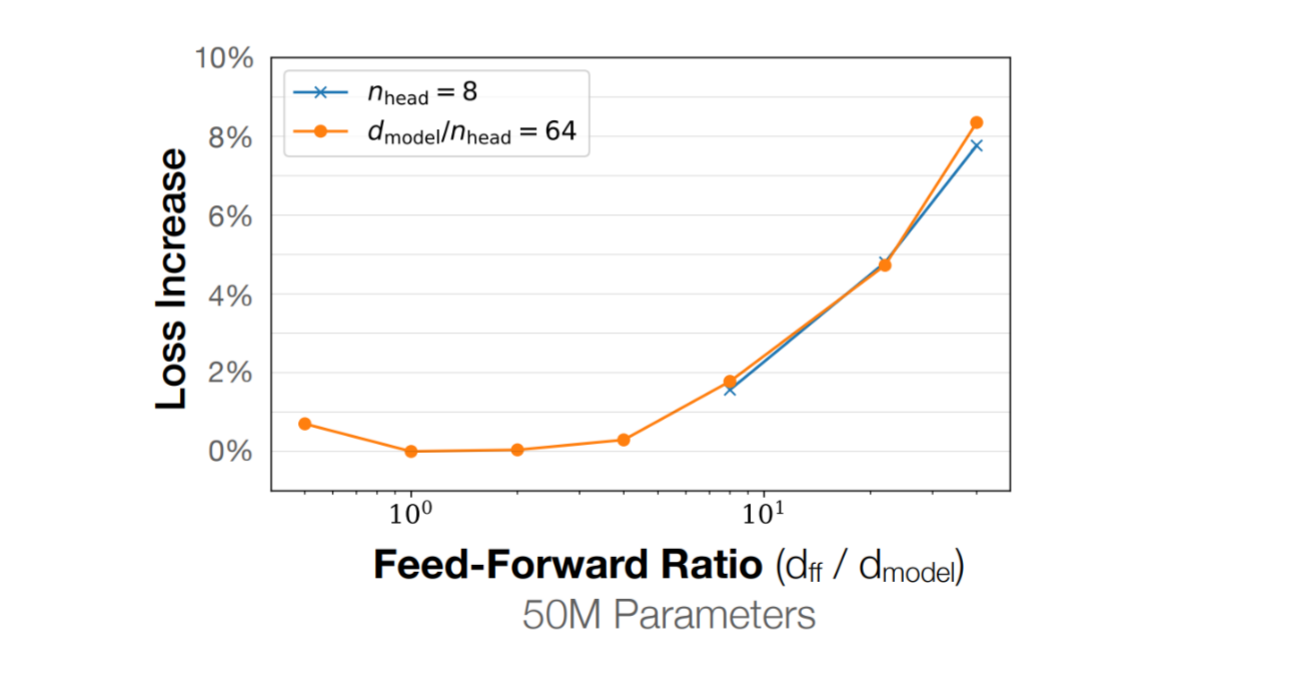
num_head和 h e a d d i m head_{dim} headdim
大部分模型都是采用下面这样的参数。
n u m h e a d × h e a d d i m = d m o d e l num_{head} \times head_{dim}=d_{model} numhead×headdim=dmodel
当然这里肯定也有一些例外,就比如上面出现的T5模型
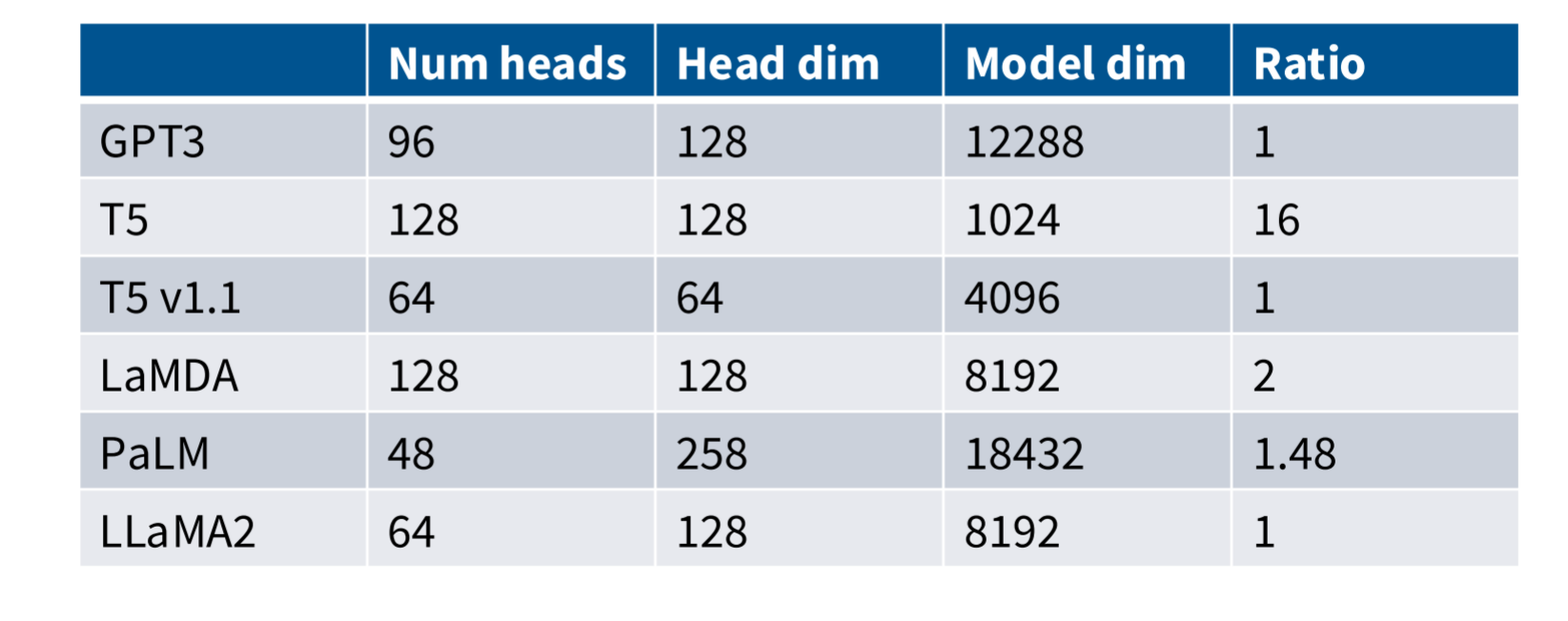
这里也就一些研究关于 n u m h e a d ∗ h e a d d i m 和 d m o d e l num_{head} * head_{dim}和d_{model} numhead∗headdim和dmodel之间比例对注意力机制表达的影响。
最开始采用1这个比例,应该也只是想参数量保持不变。
模型的高宽比 d m o d e l / n l a y e r d_{model}/n_{layer} dmodel/nlayer
更宽的网络意味着网络的效率更高,而更深的网络可能意味着网络的表达和理解能力更强。
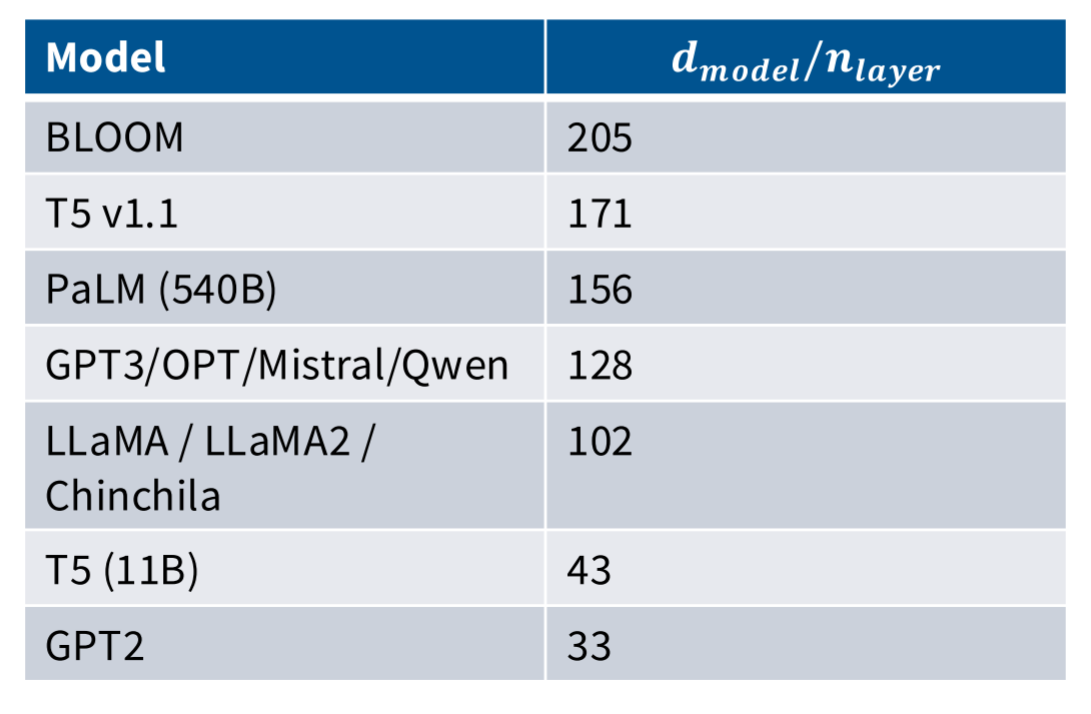
对于极深的网络并行是比较困难的。
因为模型计算本身是串行的,也就是说上一层计算完后才会将计算结果传递到下一层,下一层 才能开始计算,如果想要并行计算就需要对模型进行划分,然后采用流水线技术,这对于模型的设计提出了一定的限制。
而扩展宽度可以使用张量并行(tensor parallel),只需要将矩阵切片后部署到分布式的GPU集群就可以进行并行运算了。
当然这里也有研究关于这里比例和训练模型时损失的关系,在两者比例为100左右时,损失有最小值。
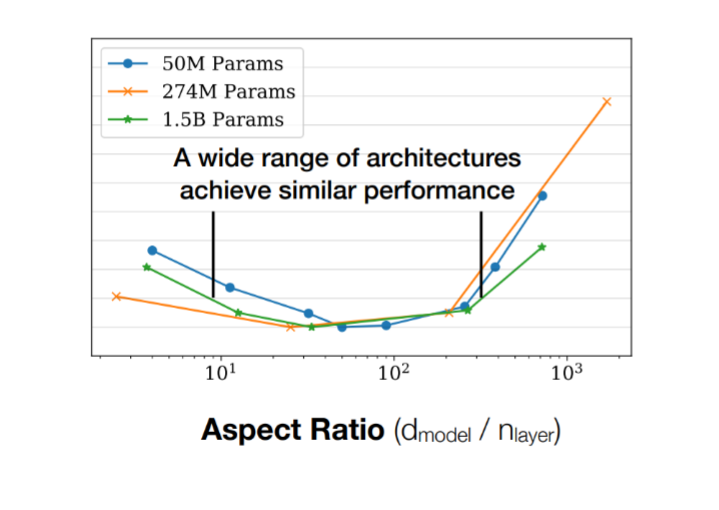
词表大小 vocabulary size
词表大小的变化趋势是越来越大的,早期的单语言模型的词表大约在30K~50K之间,现在的多语言模型的词表在100 ~ 250K之间
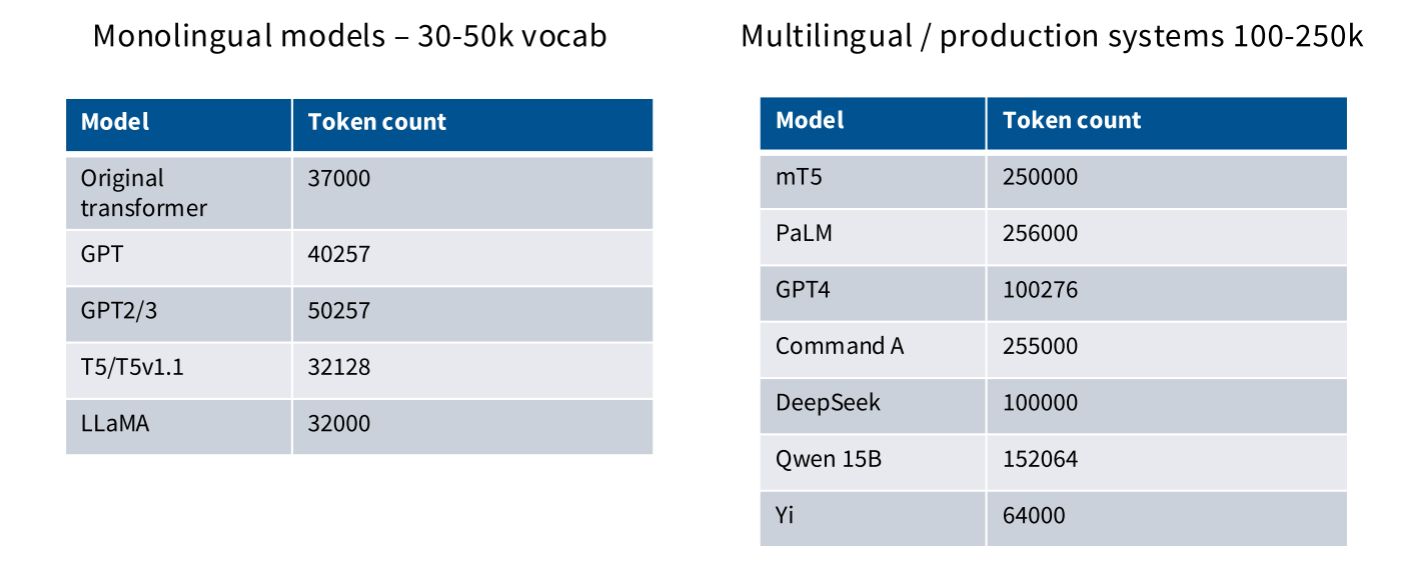
三、 正则化
在pre-train阶段基本上不会考虑正则化,因为一般pre-train的数据集非常大,基本上只会进行一个epoch的训练,很难会出现过拟合的情况,所以一般不太会考虑正则化。
于是很容易得出pre-train不需要正则化,但实际情况却不像理论分析这样。
实际上现在的模型在训练过程中会采用weight decay,这是因为weight decay的作用并非防止过拟合,weight decay是为了模型更好的训练,于是weight decay在这里的作用就变成了优化和稳定模型训练
四、 稳定训练过程的 trick
导致LLM训练不稳定的因素有很多,这里需要关注softmax。
有两个地方用到softmax一个是最后输出头,还有一个是attention内会用到softmax
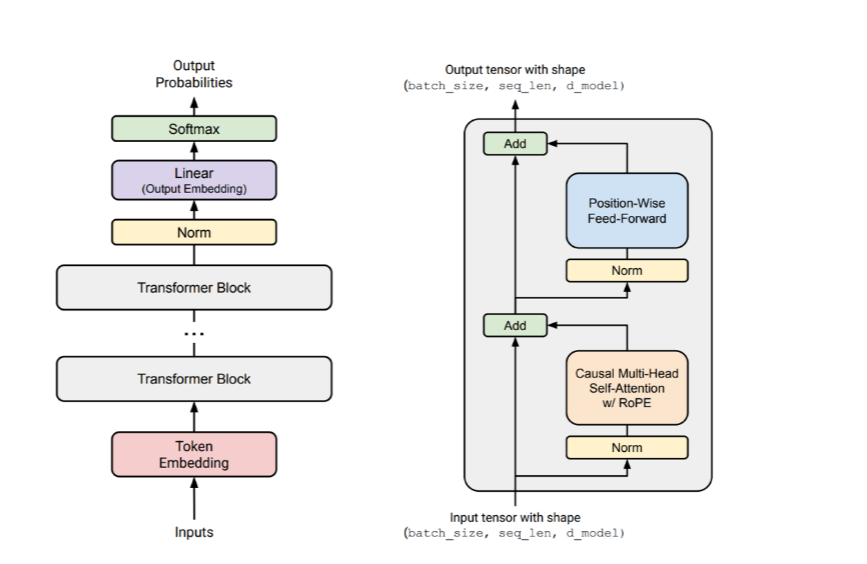
待补充
五、 注意力机制
待补充
