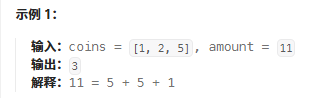java-代码随想录第38天|322. 零钱兑换、279.完全平方数、139.单词拆分
目录
322. 零钱兑换
279.完全平方数
139.单词拆分
学习链接:代码随想录
322. 零钱兑换
链接:322. 零钱兑换 - 力扣(LeetCode)
题目:
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回
-1。你可以认为每种硬币的数量是无限的。
题解:
1.确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
2.确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
3.dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
4.确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = max;}//当金额为0时需要的硬币数目为0dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍历:完全背包每个硬币可以选择多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != max) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}
}279.完全平方数
链接:279. 完全平方数 - 力扣(LeetCode)
题目:
给你一个整数
n,返回 和为n的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,
1、4、9和16都是完全平方数,而3和11不是。
题解:
1.确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j]
2.确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
3.dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?
看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, ...),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。
非0下标的dp[j]应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
4.确定遍历顺序
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];// 初始化for (int j = 0; j <= n; j++) {dp[j] = max;}// 当和为0时,组合的个数为0dp[0] = 0;// 遍历背包for (int j = 1; j <= n; j++) {// 遍历物品for (int i = 1; i * i <= j; i++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}139.单词拆分
链接:139. 单词拆分 - 力扣(LeetCode)
题目:
给你一个字符串
s和一个字符串列表wordDict作为字典。如果可以利用字典中出现的一个或多个单词拼接出s则返回true。注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
题解:
1.确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
2.确定递推公式
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
3.dp数组如何初始化
从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。
那么dp[0]有没有意义呢?
dp[0]表示如果字符串为空的话,说明出现在字典里。
但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况,那么dp[0]初始为true完全就是为了推导公式。
下标非0的dp[i]初始化为false,只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。
4.确定遍历顺序
题目中说是拆分为一个或多个在字典中出现的单词,所以这是完全背包。
还要讨论两层for循环的前后顺序。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public boolean wordBreak(String s, List<String> wordDict) {boolean[] dp=new boolean[s.length()+1];dp[0]=true;//排列问题,先背包后物品for(int i=1;i<=s.length();i++){for(String word:wordDict){int len=word.length();if(i>=len && dp[i-len] && word.equals(s.substring(i-len,i))){dp[i]=true;break;}}}return dp[s.length()];}
}