当前位置： 首页 > news >正文

5.吴恩达机器学习—神经网络的基本使用

news 2025/10/1 12:52:50

目录

一、神经网络基本概念

1.什么是神经网络

2.激活向量计算与前向传播算法

二、TensorFlow

1.TensorFlow和Numpy中数据表示对比

2.向前传播和学习实现

1.原始写法

2.在TensorFlow中简化写法

3.从头实现向前传播

三、使用TensorFlow实现线性回归和逻辑回归

1.实现不带激活函数的线性回归

2.实现带激活函数的逻辑回归

四、初步实现一个神经网络模型

1.数据归一化

2.增加数据

3.实现神经网络层

4.使用Numpy实现隐藏层函数

五、矩阵-矩阵运算实现隐藏层函数

一、神经网络基本概念

1.什么是神经网络

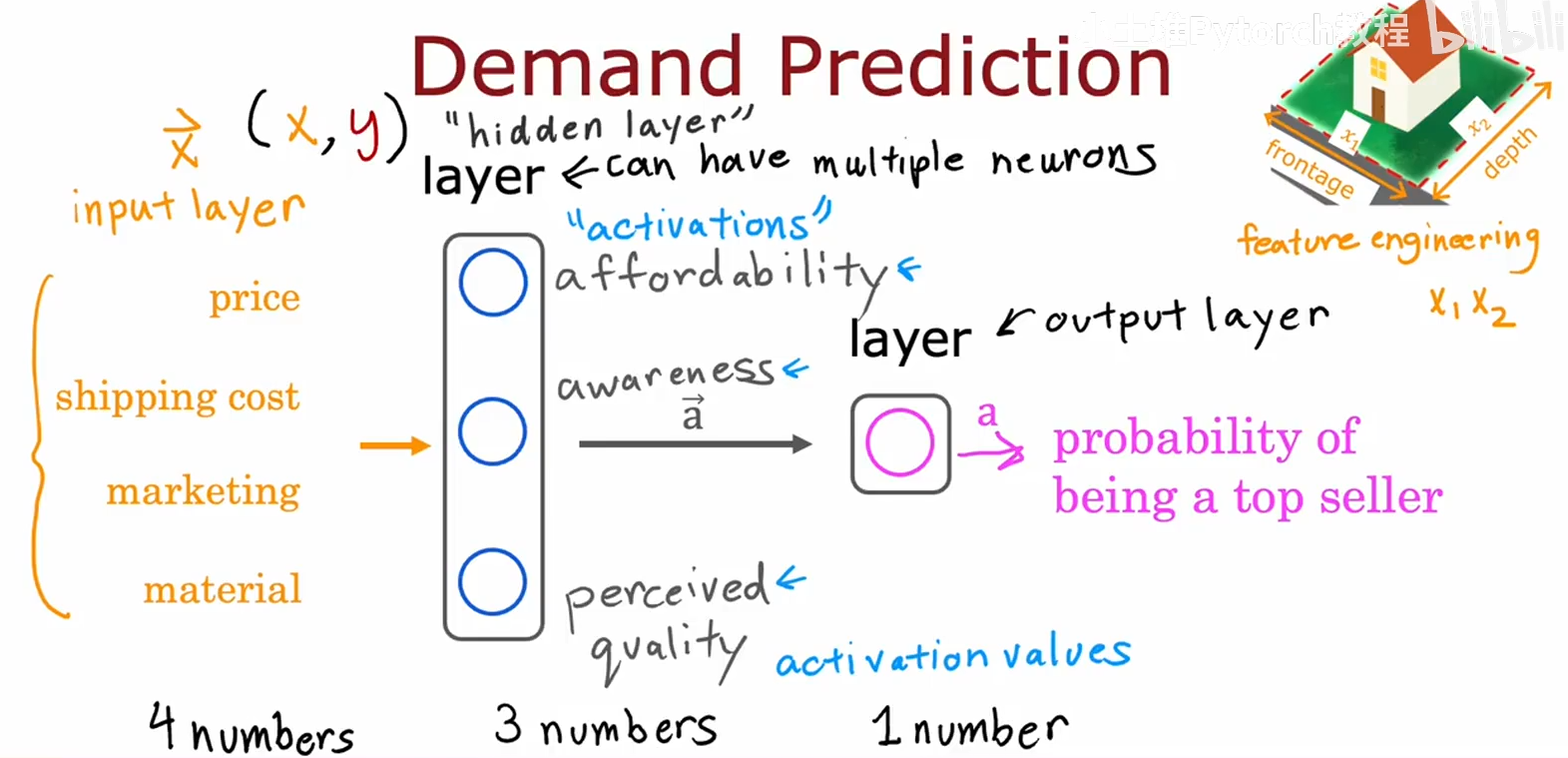
  • 神经网络由三大部分组成，输入层，中间层（隐藏层），输出层，我们将输入层简化为向量X，它是一个特征向量；隐藏层产生的结果简化为向量a，它叫做激活向量，隐藏层不止一层；输出层就是最后神经网络预结果的概率，也叫最终激活值或最终预测；
  • 神经网络最显著的特点是，当你进行训练时候，不必知道隐藏层的特征有哪些，在训练神经网络时，它会自己寻找并进行训练

2.激活向量计算与前向传播算法

  • sigmoid函数就是激活函数之一，我们把输入层向量X规定为

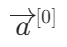
  • 前向传播算法就是指当你计算隐藏层时候，你会从输入层开始向右一层一层进行计算。同时还有反向传播算法，这将在后文提及

二、TensorFlow

1.TensorFlow和Numpy中数据表示对比

  • x = np.array([[200,17]]) 这会得到一个 1x2的二维矩阵 [200 17]
  • x = np.array([[200],[17]]) 这会得到一个 1x2的二维矩阵

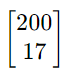
  • 而在之前的线性回归和逻辑回归中，我们经常使用x = np.array([200,17]),这只会的到一个一维向量
  • 在TensorFlow中，我们是通过矩阵而不是一维数组来表示数据，这会使得TensorFlow在内部计算上更高效

2.向前传播和学习实现

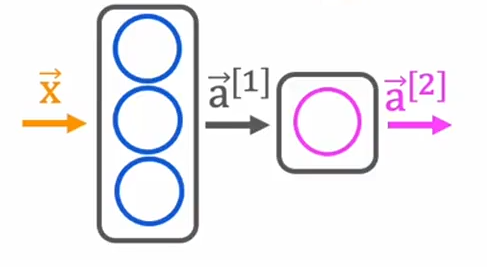
1.原始写法

这是一种显示的书写方式，直接展现了每一层的相关信息，逐层的前向传播计算

x = np.array([[200.0,17.0]])
layer_1 = Dense(units = 3,activation="sigmoid")
a1 = layer_1(x)layer_2 = Dense(units = 1,activation="sigmoid")
a2 = layer_2(a1)

2.在TensorFlow中简化写法

# 隐藏层定义
layer_1 = Dense(units = 3,activation="sigmoid")
layer_2 = Dense(units = 1,activation="sigmoid")
model = Sequential([layer_1,layer_2])
# 数据定义
x = np.array([[200.0,17.0],[120.0,5.0],[425.0,20.0],[212.0,18.0]])
y = np.array([1,0,0,1])# 模型训练
model.compile(...) # 在后文中会解释如何使用
model.fit(x,y)
# 模型预测
model.predict(x_new)

更简化的写法是

# 将以下代码
layer_1 = Dense(units = 3,activation="sigmoid")
layer_2 = Dense(units = 1,activation="sigmoid")
model = Sequential([layer_1,layer_2])# 修改为
model = Sequential([Dense(units = 3,activation="sigmoid"),Dense(units = 1,activation="sigmoid")
])

3.从头实现向前传播

  1. 这是我们要使用的w参数，在定义时候，使用以下定义，将其定义为2x3的矩阵

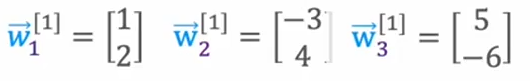
  1. 然后是b参数的定义和实现

  1. 然后定义初始的输入层，也就是a0

  1. 实现密集层函数Dense(),在前文有所提及

  • units表示的是该层中的单元数
  • a_out初始化定义为一个与units相同数量的0数组，表示我们需要使用到的激活函数的个数
  • 接下来通过循环实现
    • w = W[:,j] 表示是取得w的第一列数据，也就是我们的w1
    • z = np.dot(w,a_in)+ b[j] 和 a_out[j] = g(z) 计算的是最后通过激活函数计算要输出给下一层的激活值，激活函数在外部定义，不一定是sigmoid函数
  1. 密集函数顺序连接实现

  • 直接按照顺序实现每一层的激活值的计算，并进行向前传播，最后得到输出层的最后结果

三、使用TensorFlow实现线性回归和逻辑回归

Tips：Sequential model 官方源码

1.实现不带激活函数的线性回归

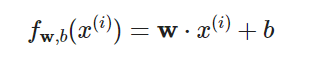
# 构建的数据集是二维矩阵
X_train = np.array([[1.0], [2.0]], dtype=np.float32)           #(size in 1000 square feet)
Y_train = np.array([[300.0], [500.0]], dtype=np.float32)       #(price in 1000s of dollars)
# 实现隐藏层，设置单元数为1，激活函数就是普通的线性函数
linear_layer = tf.keras.layers.Dense(units=1, activation = 'linear', )
# 索引操作会降维，所以当我们单独取出X_train[0]需要进行重塑为1x1的矩阵
# 如果直接使用X_train，便不需要进行重塑
a1 = linear_layer(X_train[0].reshape(1,1))# 设置权重和偏置，注意w参数也是矩阵
set_w = np.array([[200]])
set_b = np.array([100])
linear_layer.set_weights([set_w, set_b])# 比较使用TensorFlow和初始实现模型，利用X的某个数据
# 来和之前实现的模型进行比较
a1 = linear_layer(X_train[0].reshape(1,1))
print(a1)
alin = np.dot(set_w,X_train[0].reshape(1,1)) + set_b
print(alin)

2.实现带激活函数的逻辑回归

# 构建的数据集是二维矩阵
X_train = np.array([0., 1, 2, 3, 4, 5], dtype=np.float32).reshape(-1,1)  # 2-D Matrix
Y_train = np.array([0,  0, 0, 1, 1, 1], dtype=np.float32).reshape(-1,1)  # 2-D Matrix# 获取Y_train为1的数据，或者为0的数据
pos = Y_train == 1
neg = Y_train == 0
X_train[pos]# 使用Sequential创建一个线性堆叠的神经网络模型model = Sequential([tf.keras.layers.Dense(1, input_dim=1,  activation = 'sigmoid', name='L1')]# 该层只有一个神经单元，输入数据的特征维度为 1，使用 sigmoid 激活函数，该层的名称是L1
)# 定义隐藏层
logistic_layer = model.get_layer('L1')# 设置权重和偏置
set_w = np.array([[2]])
set_b = np.array([-4.5])
logistic_layer.set_weights([set_w, set_b])# 进行对比
a1 = model.predict(X_train[0].reshape(1,1))
print(a1)
alog = sigmoidnp(np.dot(set_w,X_train[0].reshape(1,1)) + set_b)
print(alog)

四、初步实现一个神经网络模型

# 加载数据
X,Y = load_coffee_data();

1.数据归一化

在前文中我们已经知道了数据归一化的相关内容，进行归一化之后，将权重拟合到数据的过程会进行得更快，数据中的每个特征都被归一化到相似的范围。下面的程序使用了Keras归一化层，他有以下步骤：

  • 创建一个“归一化层”，注意，此处应用的并非你模型中的一个层。
  • “适配”数据，这会学习数据集的均值和方差并在内部保存这些值。
  • 归一化数据，对任何利用所学模型的未来数据应用归一化非常重要。
norm_l = tf.keras.layers.Normalization(axis=-1)
norm_l.adapt(X)  # learns mean, variance
Xn = norm_l(X)

2.增加数据

# 将Xn数组在第一个维度复制1000次，第二个维度复制1次（保持不变）
# 一行为一个数据，一列是数据中的特征数
# 增加数据规模，并没有增加数据的特征，所以对第一个维度复制1000次
# 第一个维度就是数据量
Xt = np.tile(Xn,(1000,1))
Yt= np.tile(Y,(1000,1))   
print(Xt.shape, Yt.shape)

3.实现神经网络层

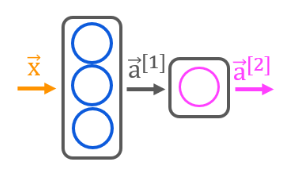
网络是由两层具有sigmoid激活函数层构成

tf.random.set_seed(1234)
model = Sequential([# 指定了输入的预期形状# 这使得TensorFlow能够在此处确定权重和偏差参数的大小# 在实际应用中可以省略，model.fit中输入指定数据时候# 会确定参数大小tf.keras.Input(shape=(2,)),# 设计两层网络，第一个参数表示层中单元数# 第二个表示层中的激活函数Dense(3, activation='sigmoid', name = 'layer1'),Dense(1, activation='sigmoid', name = 'layer2')]
)model.summary()
# 使用model.summary()可以得到网络的一些基本情况# 使用compile和fit运行梯度下降函数，进行数据拟合
# 之后的内容中会进行详细介绍
model.compile(loss=tf.keras.losses.BinaryCrossentropy(),optimizer=tf.keras.optimizers.Adam(0.001),
)model.fit(X,y,epochs=20
)

4.使用Numpy实现隐藏层函数

def my_dense(a_in, W, b, g):"""Computes dense layerArgs:a_in (ndarray (n, )) : Data, 1 example 输入数据W    (ndarray (n,j)) : Weight matrix, n features per unit, j unitsb    (ndarray (j, )) : bias vector, j units  偏置g    activation function (e.g. sigmoid, relu..)激活函数Returnsa_out (ndarray (j,))  : j units"""units = W.shape[1] # 获取该层的单元数a_out = np.zeros(units) # 创建基于单元数的维度的输出矩阵# 循环计算每一个单元for j in range(units):# W[:,j]表示获取W的列向量# 根据之前的计算公式，进行计算z = np.dot(a_in,W[:,j]) + b[j]# 最后使用激活函数a_out[j] = g(z)return(a_out)# 使用以下函数一次创建三层神经网络
def my_sequential(x, W1, b1, W2, b2, W3, b3):a1 = my_dense(x,  W1, b1, sigmoid)a2 = my_dense(a1, W2, b2, sigmoid)a3 = my_dense(a2, W3, b3, sigmoid)return(a3)

五、矩阵-矩阵运算实现隐藏层函数

关键函数：np.matmul()，这个函数可以实现矩阵的运算，一行和一列相乘，但是最后得到的是一个矩阵

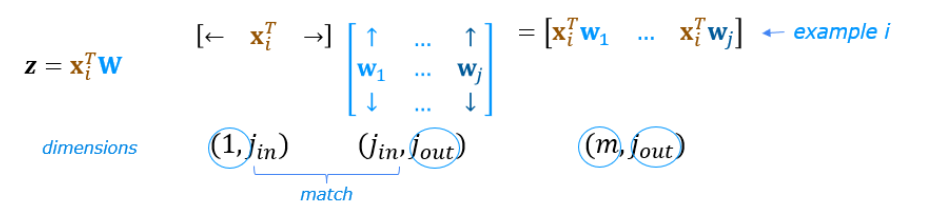
如果只有一个输入元素

x = X[0].reshape(-1,1)         # column vector (400,1)
z1 = np.matmul(x.T,W1) + b1    # (1,400)(400,25) = (1,25)
a1 = sigmoid(z1)
print(a1.shape)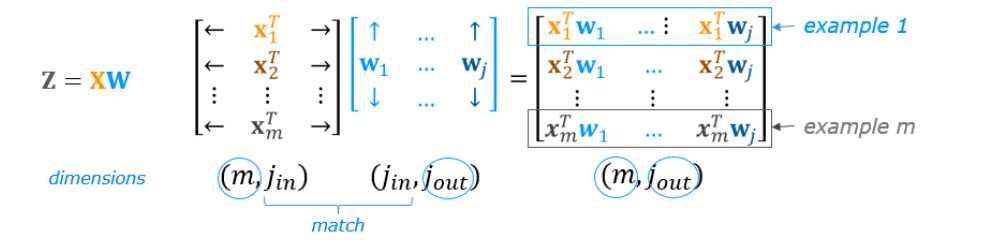

拓展到一般情况,X和W矩阵运算

def my_dense_v(A_in, W, b, g):"""Computes dense layerArgs:A_in (ndarray (m,n)) : Data, m examples, n features eachW    (ndarray (n,j)) : Weight matrix, n features per unit, j unitsb    (ndarray (j,1)) : bias vector, j units  g    activation function (e.g. sigmoid, relu..)ReturnsA_out (ndarray (m,j)) : m examples, j units"""Z = np.matmul(A_in,w) + bA_out = g(z)return(A_out)# 测试代码
X_tst = 0.1*np.arange(1,9,1).reshape(4,2) # (4 examples, 2 features)
# X_tst =
# [[0.1 0.2]
#  [0.3 0.4]
#  [0.5 0.6]
#  [0.7 0.8]]表示有 4 个样本，每个样本 2 个特征。
# 一行为一个样本
W_tst = 0.1*np.arange(1,7,1).reshape(2,3) # (2 input features, 3 output features)
# W_tst =
# [[0.1 0.2 0.3]
#  [0.4 0.5 0.6]]表示 权重矩阵，从 2 输入特征 → 3 输出单元。
# 一列为一个w
b_tst = 0.1*np.arange(1,4,1).reshape(1,3) # (3 features, 1)
# b_tst =
# [[0.1 0.2 0.3]]表示 偏置向量，长度为 3，对应输出层的 3 个单元。
A_tst = my_dense_v(X_tst, W_tst, b_tst, sigmoid)
print(A_tst)# 同4.4代码
def my_sequential_v(X, W1, b1, W2, b2, W3, b3):A1 = my_dense_v(X,  W1, b1, sigmoid)A2 = my_dense_v(A1, W2, b2, sigmoid)A3 = my_dense_v(A2, W3, b3, sigmoid)return(A3)
http://www.dtcms.com/a/428381.html

相关文章：

  • OSPF协议详解1：从基础概念到区域划分与报文类型解析
  • 广州哪里做公司网站号一级造价工程师报考条件及科目
  • 数据结构算法学习：LeetCode热题100-普通数组篇（最大子数组和、合并区间、轮转数组、除自身以外数组的乘积、缺失的第一个正常数）
  • JAVA爬虫实战项目——OKX解析
  • 解除网站开发合同 首付款是否退长沙公司网站设计报价
  • DOM CSS：深入理解与高效运用
  • 闵行网站建设外包微信营销策略有哪些
  • 创建网站怎么赚钱的如何做一个好网站
  • Elasticsearch - Linux下使用Docker对Elasticsearch容器设置账号密码
  • 10. Spring AI + RAG
  • wordpress做自建站上海高品质网站建设公司
  • 网站开发如何找甲方网站后台维护费用
  • 智能化企业级CRM系统开发实战飞算JavaAI全流程体验
  • Matlab通过GUI实现点云的PCA配准(附最简版)
  • 10.17 上海 Google Meetup：从数据出发，解锁 AI 助力增长的新边界
  • 免费成品网站下载上海网站设计多少钱
  • 外管局网站上做预收登记制作公司网页图片
  • 【DockerFile+Nginx+DockerCompose】前后端分离式项目部署(docker容器化方式)
  • 快速傅里叶变换简介及python实现
  • 网站的实现怎么写重庆网站seo方法
  • 公司建设网站费用会计分录哈尔滨建筑工程招聘信息
  • 猫眼网站建设适合小县城开的加盟店
  • 网站开发 系统需求文档个性化定制网站
  • IDEA+SpringBoot实现远程DEBUG到本机
  • 网站建设与维护 目录开发公司前期手续流程
  • 物品奖励系统介绍
  • 广州站西手表公司彩页设计制作
  • sat4j中参数作用
  • 网站建设课程有哪些收获西安注册公司虚拟地址
  • 哪家做网站性价比高朋友圈自己做的网站