快速傅里叶变换简介及python实现

一、傅里叶变换简介

1.1傅里叶级数（Fourier Serie）

在数学和信号分析处理等多个领域中，法国数学家傅里叶提出的傅里叶级数和变换理论被广泛使用，该理论的核心思想可概括为：在一定条件下，任何一个复杂函数可以表示为不同频率的正弦函数之和，如下图所示，图中最底部的函数是上面4个函数之和：

不同频率的正弦函数之和就是傅里叶级数，公式如下：


f(t)是连续变量t的函数，Cn是系数。

1.2傅里叶变换（Fourier Transform，FT）

傅里叶变换可分为连续傅里叶变换和离散傅里叶变换，分别针对的分析对象是连续信号或离散信号。
连续傅里叶变换（Continuous Fourier Transform，CFT）主要用于分析真实世界的连续信号，正变换和反变换公式如下：


f(t)是连续变量t的连续函数，F(u)是傅里叶变换函数。

离散傅里叶变换（Discrete Fourier Transform，DFT）主要用于处理对真实世界取样得到的离散信号，例如一维振动信号，二维数字图像。正变换和反变换公式如下：


在现实信号分析处理中，主要使用的是离散傅里叶变换，而为了提高计算效率，在离散傅里叶变换的基础上提出了快速傅里叶变换。

1.3快速傅里叶变换（Fast Fourier Transform，FFT）

快速傅里叶变换是计算离散傅里叶变换的快速算法，基本思想是利用DFT复指数的对称性和周期性等特性，将长序列分解为短序列的DFT实现整个序列的DFT，比较常用的基2FFT算法，可将算法复杂度降至DFT的对数级别。

基2FFT算法可分为按时间抽取和按频率抽取，按时间抽取可使用蝶形结构的流程图表示，如下图：

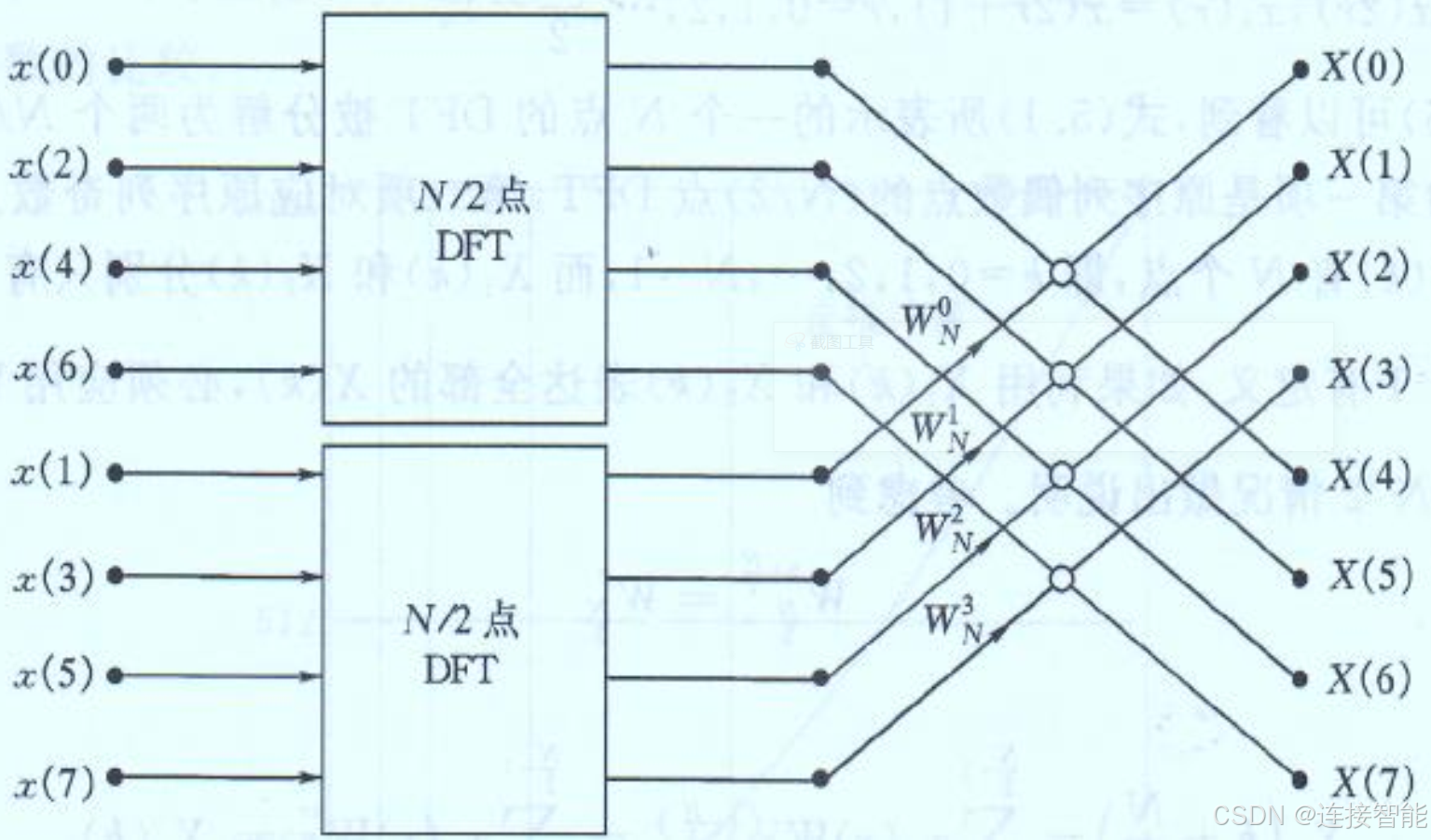
上图是将原始序列按照奇偶进行分解，分解成两组，而这两组又可以分别继续进行分解，最终实现对数级算法复杂度。
计算公式如下：

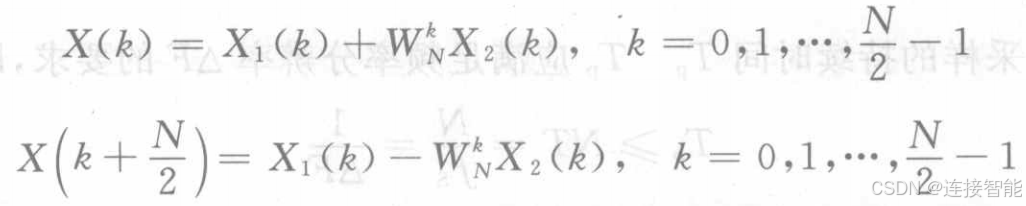
二、快速傅里叶变换python实现

2.1关键说明

本节使用python编写一个完整的按时间抽取的基2FFT算法，而与python中现成的FFT函数包区别如下：

1. 代码在执行效率上不如现成的函数包；
2. 且要求输入序列长度为2的指数次幂，否则会输出错误结果，而现有的FFT函数包如numpy的FFT函数可接受任意长度的序列；
3. 本节代码的主要用途是帮助更好地理解算法原理。

2.2代码实现

def FastFourierTransform_1D(origin_seq):def butterfly(tmp_seq):tmp_len = len(tmp_seq)half_len = tmp_len // 2x1 = tmp_seq[0:half_len]x2 = tmp_seq[half_len:tmp_len]new_data_seq = np.arange(tmp_len, dtype = complex)for k in range(half_len):weight = np.exp(-2j * np.pi * k / tmp_len)new_data_seq[k] = x1[k] + weight * x2[k]new_data_seq[half_len + k] = x1[k] - weight * x2[k]return new_data_seqseq_len = len(origin_seq)if seq_len == 1:return origin_seqseq_even = FastFourierTransform_1D(origin_seq[0::2])seq_odd = FastFourierTransform_1D(origin_seq[1::2])fft_seq = butterfly(np.concatenate((seq_even, seq_odd)))return fft_seq

2.3代码说明

代码主体是一个一维FFT变换函数FastFourierTransform_1D，接收输入的变量origin_seq应为一维numpy数组，返回输出的是FFT变换后的序列。

1. 代码主体使用递归形式，调用自身，对序列进行奇偶分解；
2. 奇偶序列分解计算FFT之后，通过子函数butterfly计算出原始序列的FFT；
3. butterfly函数内部按照1.3小节公式进行计算，计算过程使用复数计算。