当前位置：首页 > news >正文

PostgreSQL 向量操作符的计算和使用方式

news 2025/10/1 11:53:25

PostgreSQL 向量操作符的计算和使用方式

- 一. 概述
- 二. 向量操作符列表
- 三. 操作符计算公式
- - 3.1 <-> L2 距离（欧氏距离）
  - 3.2 <#> 负内积
  - 3.3 <=> 余弦距离
  - 3.4 <+> L1 距离（曼哈顿距离）
  - 3.5 <~> 汉明距离（Binary vectors）
  - 3.6 <%> Jaccard 距离（Binary vectors）
- 四. 建索引优化查询
- 五. 总结

前言
这是我在这个网站整理的笔记,有错误的地方请指出，关注我，接下来还会持续更新。

作者：神的孩子都在歌唱

一. 概述

pgvector 是 PostgreSQL 的一个扩展，用于存储和检索高维向量，常用于语义搜索、推荐系统、图像检索等场景。

向量检索的核心操作是 计算查询向量与数据库中向量的相似度，pgvector 提供多种操作符支持不同的相似度计算方式，包括欧氏距离、内积、余弦距离、曼哈顿距离、汉明距离和 Jaccard 距离。

二. 向量操作符列表

操作符	距离/相似度度量	说明	数据类型	推荐场景
`<->`	L2 距离 (Euclidean)	几何距离	实数向量	图像、音频、地理数据检索
`<#>`	负内积 (Negative Inner Product)	内积取负，用于最大内积搜索	实数向量	推荐系统、模型打分
`<=>`	余弦距离 (Cosine Distance)	1 - 余弦相似度，长度归一化	实数向量	文本语义检索、跨语言向量匹配
`<+>`	L1 距离 (Manhattan Distance)	各维度差值绝对值之和	实数向量	对异常值敏感的特征空间检索
`<~>`	汉明距离 (Hamming Distance)	二进制向量中不同位数	二进制向量	二进制向量、编码匹配
`<%>`	Jaccard 距离 (Jaccard Distance)	集合、稀疏二进制向量匹配	交集	集合、稀疏二进制向量匹配

距离越小越相似

三. 操作符计算公式

3.1 <-> L2 距离（欧氏距离）

$\sqrt{\sum_{i=1}^{n} (q_i - v_i)^2}$

例子
q = [1,2,3], v = [4,0,5]
$\sqrt{(1-4)^2 + (2-0)^2 + (3-5)^2} = \sqrt{17} \approx 4.123$
SQL 示例

SELECT id,embedding, embedding <-> '[1,2,3]' as score
FROM documents
ORDER BY embedding <-> '[1,2,3]'
LIMIT 5;

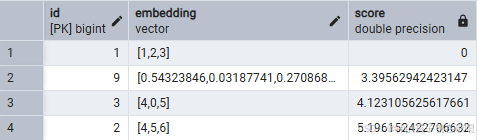
在这里插入图片描述

3.2 <#> 负内积

$\sum_i q_i v_i$

例子
q = [1,2,3], v = [4,0,5]
$\cdot v = 19 \implies d = -19$
SQL 示例

SELECT id
FROM documents
ORDER BY embedding <#> '[1,2,3]'
LIMIT 5;

负内积

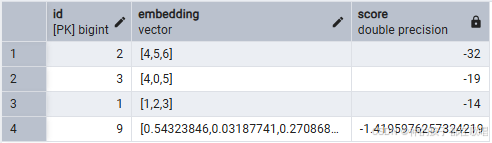
3.3 <=> 余弦距离

$\frac{q \cdot v}{||q|| \cdot ||v||}, \quad ||q|| = \sqrt{\sum_i q_i^2}$

例子
q = [1,2,3], v = [4,0,5]

内积：q·v = 19
模长：||q|| = √14 ≈ 3.742, ||v|| = √41 ≈ 6.403
余弦距离：1 - 19 / (3.742*6.403) ≈ 0.207

SQL 示例

SELECT id
FROM documents
ORDER BY embedding <=> '[1,2,3]'
LIMIT 5;

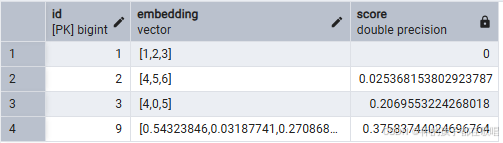
在这里插入图片描述

3.4 <+> L1 距离（曼哈顿距离）

$\sum_i |q_i - v_i|$

例子
q = [1,2,3], v = [4,0,5] → d = 7

SQL 示例


SELECT id, embedding, embedding <+> '[1,2,3]' as score
FROM documents
ORDER BY embedding <+> '[1,2,3]'
LIMIT 5;

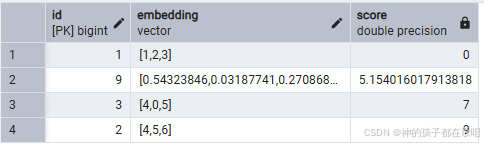
在这里插入图片描述

3.5 <~> 汉明距离（Binary vectors）

$\text{count of differing bits(不同的位数)}$

例子
q = 10101, v = 10011 → 不同位 = 2

SQL 示例

SELECT id, data
FROM binary_vector
ORDER BY data <~> B'10101'
LIMIT 5;

3.6 <%> Jaccard 距离（Binary vectors）

$\frac{|q \cap v|}{|q \cup v|}$

例子
q = 10101, v = 10011 → 交集 10001 = 2 位, 并集 10111 = 4 位
d = 1 - 2/4 = 0.5

SQL 示例

SELECT id, data
FROM binary_vector
ORDER BY data <%> B'10101'
LIMIT 5;

四. 建索引优化查询

为了提升检索效率，可使用 IVFFlat 索引：

-- L2距离
CREATE INDEX idx_l2 ON documents USING ivfflat (embedding vector_l2_ops) WITH (lists = 100);-- 内积
CREATE INDEX idx_ip ON documents USING ivfflat (embedding vector_ip_ops) WITH (lists = 100);-- 余弦距离
CREATE INDEX idx_cosine ON documents USING ivfflat (embedding vector_cosine_ops) WITH (lists = 100);-- L1距离
CREATE INDEX idx_l1 ON documents USING ivfflat (embedding vector_l1_ops) WITH (lists = 100);-- 汉明距离
CREATE INDEX idx_hamming ON binary_vector USING ivfflat (data vector_hamming_ops) WITH (lists = 100);-- Jaccard距离
CREATE INDEX idx_jaccard ON binary_vector USING ivfflat (data vector_jaccard_ops) WITH (lists = 100);