小杰深度学习（four）——神经网络可解释性、欠拟合、过拟合

神经网络可解释性与欠拟合

1.1 神经网络的可解释性

神经网络的可解释性是指神经网络中每个决策或预测的可解释性。神经网络是一种黑箱模型，其决策或预测的结果往往难以解释。因此，可解释性是神经网络中的一个重要问题，它有助于助理解神经网络的行为，发现网络中的问题，并提高网络的可靠性和可信度。

通过可解释性分析，可以更好地理解神经网络的行为，发现网络中的问题，改进网络的性能和可靠性。同时，可解释性分析还可以帮助建立用户可信的神经网络系统，提高用户对系统的信任度。

提升神经网络可解释性的常用方法：

• 全连接层：在输出层前添加，辅助解析决策逻辑。
• Dropout 层：随机失活神经元抑制过拟合，间接增强可解释性。
• 归一化层：标准化输入分布，缓解梯度消失并提升特征可解释性。
• 注意力机制：聚焦关键特征，直观展现输入与预测的关联权重。

神经网络的可解释性对其应用至关重要，只有具备可解释性，才能增强人们对预测结果的信任并推动实际应用。

1.2 欠拟合的概念

欠拟合指模型在训练集上未能有效拟合数据，无法捕捉复杂关系与模式，导致训练误差和测试误差均较高。

造成欠拟合的常见原因：

1. 数据量不足：训练数据匮乏，模型无法学习到足够特征与模式，导致预测误差大。
2. 模型复杂度低：模型过于简单（如用线性模型拟合非线性数据），无法捕捉数据中的复杂关系。
3. 正则化过度：强正则化迫使模型参数趋近于零，过度简化模型，忽略重要特征。

例子：

模型因学习特征不足导致识别结果不准确，是欠拟合的典型表现，如下图所示：

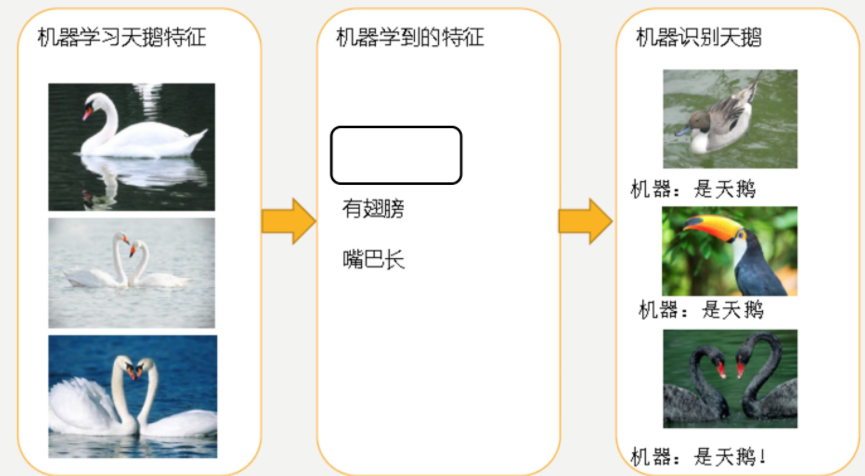
欠拟合较易解决：项目中若出现欠拟合，可通过增加数据量（如数据增强）或采用更复杂模型（如换用深层网络）改善，核心问题是模型复杂度不足或数据信息有限。

1.3 散点输入

本实验中提供了一些散点，其分布如下图所示：

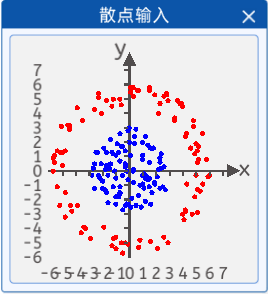
现在需要根据这些散点来拟合一条曲线来将这些点分类。

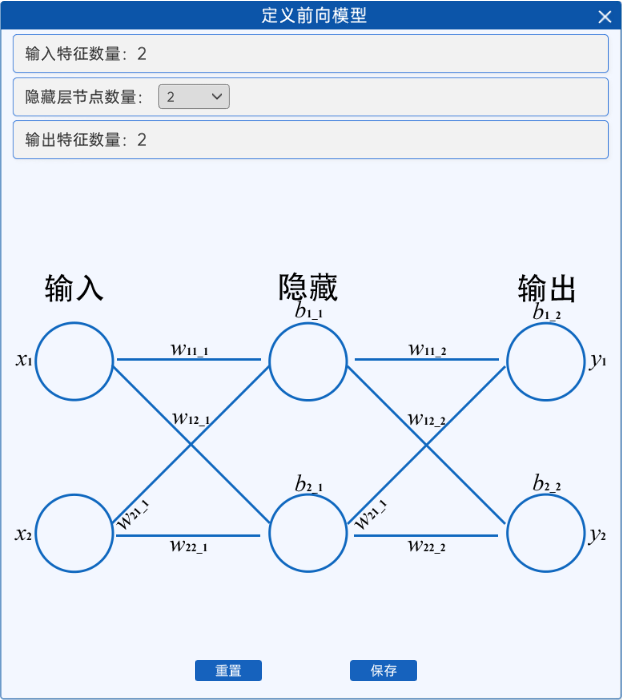
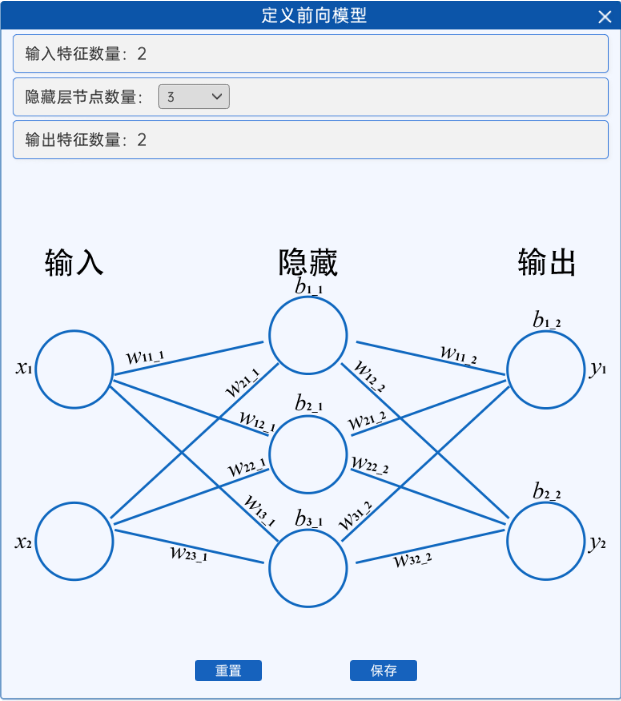
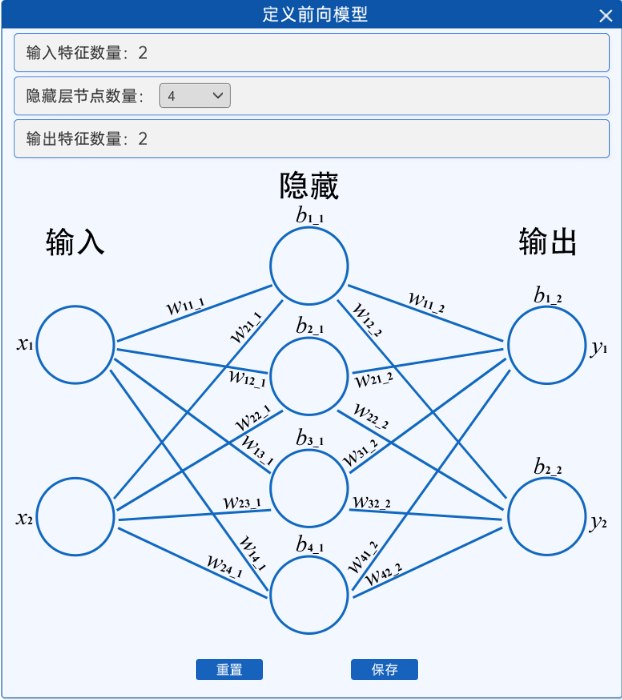
可以看到，这个神经网络其实还不是很复杂，当“隐藏层节点数量”选择“3”或“4”时，其网络结构如下图所示：

隐藏层节点数量=3	隐藏层节点数量=4

可以看到，隐藏层节点的数量越多，网络结构越复杂，其计算量也越加的复杂。

1.5 定义损失函数和优化器

前向模型定义完成后，就需要定义反向传播过程所用到的一些超参数了，在“定义损失函数和优化器”组件中，使用交叉熵损失函数。除此之外，可以自己选择学习率与优化器，优化器给出了两个选项，分别为SGD（随机梯度下降）和Adam，如下图所示：

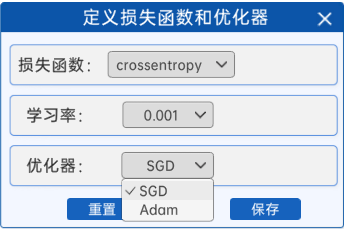
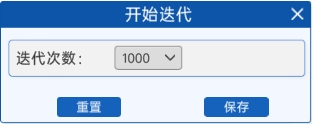
1.6 开始迭代

通过“开始迭代”组件，设置模型的训练次数。

1.7 显示频率设置

为了能够更好的观察迭代过程中的现象，可以通过“显示频率设置”组件来设置每隔多少次显示一次当前的曲线拟合状态。

1.8 拟合线显示与输出

通过“拟合线显示与输出”组件，就可以观察到迭代过程中曲线的拟合状态了。

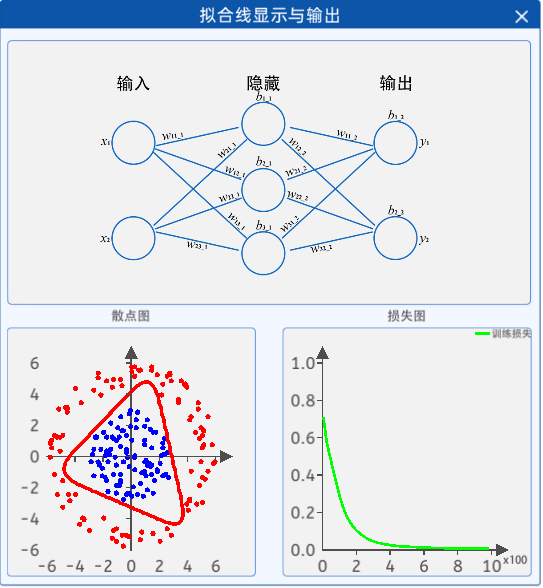
其中，参数的值会随着不断的迭代而实时更新，左边的图也是根据参数值而实时绘制的，右边的图则是以迭代次数为横坐标、损失值为纵坐标绘制的损失图。

1.9 试错

当定义前向模型中的隐藏层节点是2时，会发现永远无法形成拟合的边界，原因是一个节点对应着一条直线的w和b，两个节点只有两条直线，两条直线并不能形成闭合边界，所以最少需要三个节点才可以实现分类边界。

代码

神经网络可解释性和欠拟合有图

#神经网络可解释性和欠拟合
import numpy as np
import  torch
import  torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 1.散点输入
class1_points = np.array([[-2.8, 0.1], [0.4, 2.8], [-0.1, 1.9], [-2.0, 1.5], [-0.4, 0.4], [2.1, -0.0],[-0.8, 0.6], [0.4, -2.5], [0.1, -2.0], [-0.6, 1.6], [-1.5, 2.1], [-0.9, 1.2],[1.3, 1.7], [0.2, -0.0], [0.2, -0.1], [-2.1, -0.8], [-0.7, 1.6], [1.4, -1.2],[-0.8, -1.6], [-1.3, 1.1], [-1.2, -0.1], [-2.9, -0.4], [2.4, -1.2], [-2.7, -1.3],[-1.1, -1.9], [1.4, 0.5], [-1.0, 1.8], [2.2, 0.8], [0.9, 1.9], [1.8, -0.9],[1.4, -0.6], [-0.2, -0.7], [-0.3, -2.4], [-1.5, 0.4], [1.2, -0.5], [-1.8, 1.2],[-0.8, -1.7], [-1.7, -2.3], [-0.6, -0.4], [0.3, 1.8], [-0.9, -1.9], [1.6, -1.6],[0.8, -2.6], [-2.6, 1.2], [1.8, -1.0], [0.2, -0.9], [-0.4, -2.5], [1.5, 1.5],[2.2, -1.3], [-1.4, 1.2], [-0.4, 1.3], [-1.3, -1.2], [-2.2, 0.4], [-0.1, 2.9],[1.5, -2.4], [1.1, 2.3], [0.4, 2.8], [-0.8, -1.2], [-2.7, 0.4], [2.3, 1.1],[0.9, 1.0], [0.9, 0.7], [-1.8, 0.3], [-1.7, -0.4], [1.0, -0.3], [-1.1, -0.6],[-2.4, -0.4], [2.6, -1.4], [1.3, -0.7], [-0.0, 1.0], [-1.1, -2.4], [2.0, -0.5],[0.3, 2.3], [-0.6, -2.8], [0.6, -1.8], [0.9, -0.4], [1.0, -1.3], [-0.4, 0.2],[2.3, 0.1], [2.2, 0.5], [2.5, 0.2], [-2.1, -1.3], [-1.1, 1.0], [1.7, 1.5],[0.9, -1.0], [1.1, -2.2], [-0.2, -2.4], [0.7, -1.1], [-0.4, 0.3], [-0.0, -2.6],[-0.3, -0.1], [-1.8, -1.6], [-0.8, 2.5], [-1.9, -1.4], [-2.5, 1.2], [-2.3, -0.6],[-1.6, 0.1], [-1.9, 0.0], [1.1, -0.6], [-0.2, 2.7]])
class2_points = np.array([[5.1, 1.6], [-5.1, 1.2], [-4.6, 3.0], [-5.7, 0.5], [5.4, 2.5], [-4.5, -2.5],[4.9, -0.4], [1.4, 5.5], [1.4, 5.7], [4.2, -1.0], [-1.3, -4.8], [-4.4, -2.9],[-3.6, 3.4], [-3.4, -4.1], [-5.8, -0.1], [4.7, 3.0], [-1.4, 4.4], [2.5, -4.7],[2.7, 5.3], [4.1, -2.8], [-4.0, -2.5], [5.0, 0.5], [-4.0, 4.3], [5.0, 1.3],[3.3, 3.4], [2.2, 4.6], [2.8, 4.8], [4.0, -3.5], [4.6, -3.1], [0.5, 5.5],[-4.7, 3.1], [-5.7, 1.0], [2.8, -5.1], [-1.3, 4.9], [2.7, 5.2], [-4.9, 1.3],[4.1, -2.9], [-4.9, -3.3], [-4.6, 2.8], [-4.6, 3.1], [-1.8, 4.8], [-2.4, 5.3],[-5.2, 3.0], [-3.7, -4.4], [1.5, -5.0], [4.8, 1.1], [-0.6, -5.8], [0.7, -4.9],[0.2, 5.7], [5.8, -0.5], [-2.0, -4.0], [3.9, -3.1], [0.2, 5.1], [4.5, 1.5],[-1.4, -5.3], [5.0, -1.4], [5.1, 0.7], [5.0, -3.0], [-0.7, -5.1], [5.2, -1.5],[-0.7, 4.5], [2.1, 3.9], [-2.4, 5.0], [-0.8, 4.9], [-5.1, 0.3], [3.3, 3.6],[-0.4, -5.1], [3.8, 4.6], [-5.3, -2.5], [-5.5, -1.2], [0.6, 5.5], [-5.8, 0.8],[-5.3, 1.2], [2.0, -5.5], [5.7, 0.7], [-1.1, -4.7], [-0.0, 5.7], [-3.0, -4.8],[-3.5, -4.0], [4.9, 1.8], [-1.1, -5.5], [-2.7, 4.2], [-4.9, -1.6], [-0.2, -5.2],[2.5, 5.1], [-0.0, 5.4], [3.9, 4.4], [3.5, 4.8], [4.8, -1.9], [5.4, -1.0],[3.7, 4.6], [1.8, 5.2], [4.7, 3.4], [4.1, 2.3], [0.6, -5.4], [1.4, 5.5],[-5.5, 1.3], [4.2, 2.5], [-2.2, 3.9], [5.9, -0.4]])
#连接起来
points=np.concatenate((class1_points,class2_points),axis=0)
labels=np.concatenate((np.ones(len(class1_points)),np.zeros(len(class2_points))))
#2.定义模型
class Model(nn.Module):def __init__(self):super(Model,self).__init__()self.layer1=nn.Linear(2,4)self.layer2=nn.Linear(4,2)def forward(self,x):x=torch.sigmoid(self.layer1(x))x=self.layer2(x)return x
#7创建网格点 画等高线
xx,yy=np.meshgrid(np.linspace(-6.5,6.5,100),np.linspace(-6.5,6.5,100))
grid_points=np.c_[xx.ravel(),yy.ravel()]
#初始化模型
model=Model()
#3.定义优化器与损失函数
#定义学习率
lr=0.05
#定义损失函数（交叉熵）
cri=nn.CrossEntropyLoss()
#定义优化器
optimizer=optim.Adam(model.parameters(),lr=lr)
#4.迭代
epoches=1000
for epoch in range(1,epoches+1):#将numpy转化成tensorinput_data=torch.tensor(points,dtype=torch.float32)label_data=torch.tensor(labels,dtype=torch.long)#前向传播output=model(input_data)#计算损失loss=cri(output,label_data)#反向传播与优化#梯度清空optimizer.zero_grad()#计算梯度loss.backward()optimizer.step()print(loss.detach().cpu().item())# 5.显示频率设置if epoch == 1 or epoch % 20 == 0:print(f"epoch:{epoch},loss:{loss}")# 进行预测网格点grid_points_tensor = torch.tensor(grid_points, dtype=torch.float32)pre_result = model(grid_points_tensor).detach().numpy()# 获取其中的一类one_lables_prob = pre_result[:, 1].reshape(xx.shape)plt.cla()plt.scatter(class1_points[:, 0], class1_points[:, 1], c='r')plt.scatter(class2_points[:, 0], class2_points[:, 1], c='b')plt.contour(xx, yy, one_lables_prob, levels=[0.5])plt.pause(1)print('s')# 6.绘图
plt.show()

神经网络的过拟合

1. 原理

1.1 过拟合的概念

过拟合是指模型过于复杂，即模型对训练数据的拟合能力过强，导致模型在训练数据上的表现很好，但在测试数据上的表现较差。

例如下图，模型训练中过拟合与提前停止策略的示意图

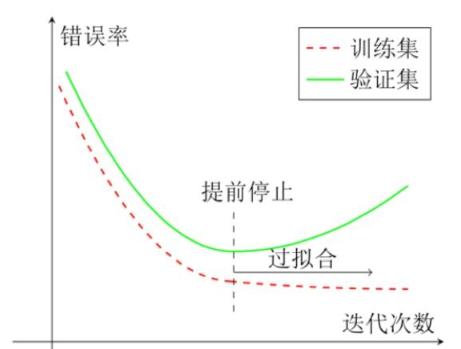
横轴是训练迭代次数（模型学习数据的轮次），纵轴是错误率（预测结果的误差）。

训练集（虚线）：迭代越多，模型对训练数据 “学” 得越熟，错误率持续下降（但可能因死记硬背偏离真实规律）。

验证集（实线）：前期随训练，错误率同步下降（模型泛化有效）；但迭代超临界点后，错误率反弹（模型开始 “死记” 训练集细节，对新数据（验证集）预测变差，即过拟合）。

提前停止：验证集错误率触底反弹前，及时终止训练（虚线标注处），可避免模型过拟合，保留较好泛化能力。

总结，这张图教你 “别让模型学太‘呆’”—— 当验证集效果从变好转向变差时，赶紧停，防止过拟合！

造成过拟合的常见原因：

1. 数据量不足，模型易过度学习训练数据噪声与细节，致测试表现差。
2. 模型过复杂，会过度学习训练数据细节、噪声，导致在测试数据上的表现较差。
3. 正则化强度不足，模型易过度学习训练数据细节、噪声，让测试表现变差（后续章节介绍正则化 ）。
4. 数据量比例不均衡，复杂模型易将少量特例当噪声去除，引发识别偏差，此为 AI 需解决的 “长尾效应”—— 因多数数据常见、少量数据特例占比低，模型学习时易忽视特例，将某些真实存在但出现频率较低的特征，错误地判定为 “不属于目标群体的普遍规律”，进而忽略或排除这些特征的现象 。

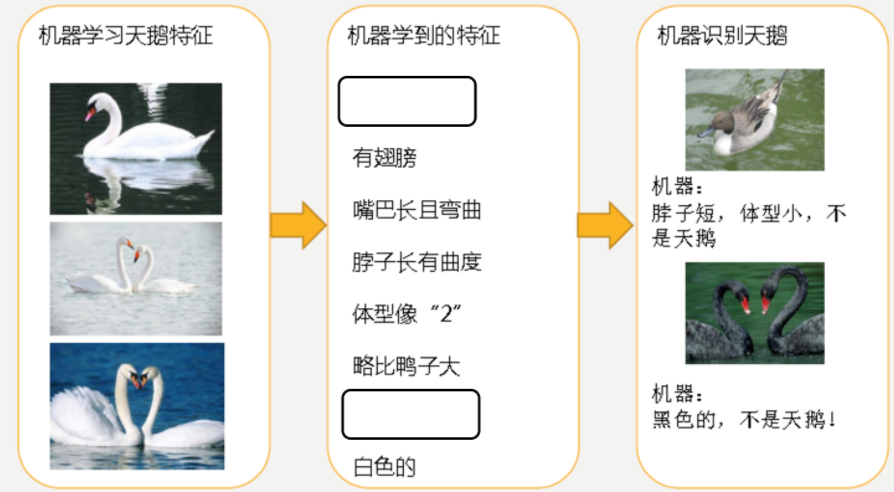
下图为有过拟合现象的例子，因模型学习的 “细节” 特征过多，识别新动物时，会因 “细节” 特征不匹配致识别结果不准。

1.2 欠拟合与过拟合的区别

欠拟合因模型学习能力不足，未能捕捉数据复杂关系；

过拟合因模型学习能力过强，过度学习训练数据细节与噪声，导致泛化能力差。

1.3 散点输入

本实验中提供了一些散点，其分布如下图所示：

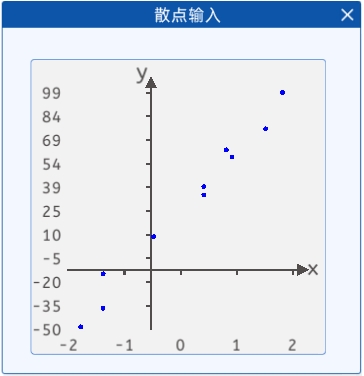
现在我们需要根据这些散点来拟合一条线。

其中，横坐标为输入特征，纵坐标为预测结果。

1.4 定义前向模型

根据上面的散点我们可以得到：最少可以使用一个来拟合这条线，但是这是提前知道可以使用一个参数w即可实现目的，但是实际上大部分的数据没办法通过绘图将其表示出来，所以就需要随便搭建一个神经网络来拟合这条曲线。在“定义前向模型”组件中，规定好了一个完整的神经网络，如下图所示。

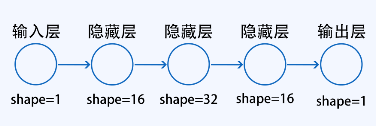
其中包含了一个输入层、三个隐藏层和一个输出层。输入层有一个节点，用来接收输入特征x；这三层隐藏层都用了很多的节点用来计算；最后输出层使用一个节点来输出拟合结果。

1.5 定义损失函数和优化器

前向模型定义完成后，就需要定义反向传播过程所用到的一些超参数了，在“定义损失函数和优化器” 组件中，我们给出了MSE（均方误差损失函数，拟合问题），并且已经选好了优化器为Adam，为了保证能够过拟合，所以学习率也固定为0.005，如下图所示：

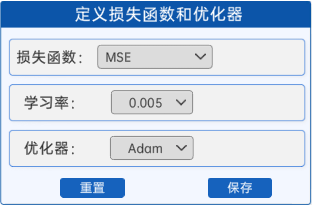
1.6 开始迭代

通过“开始迭代”组件，设置模型的训练次数。

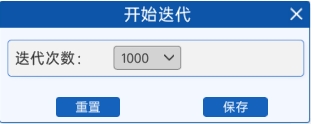
1.7 显示频率设置

为了能够更好的观察迭代过程中的现象，可以通过“显示频率设置”组件来设置每隔多少次显示一次当前的曲线拟合状态。

1.8 拟合线显示与输出

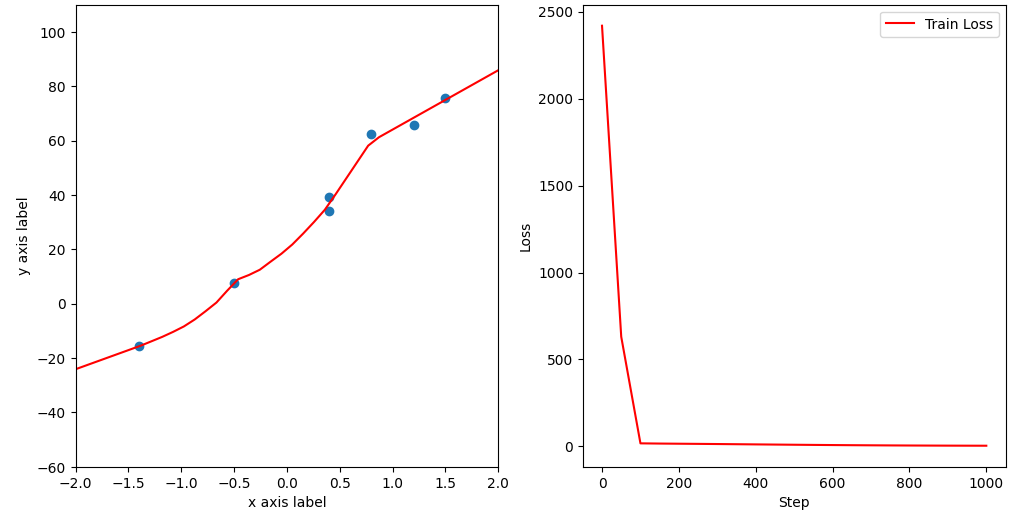
通过“拟合线显示与输出”组件，就可以观察到迭代过程中曲线的拟合状态了。

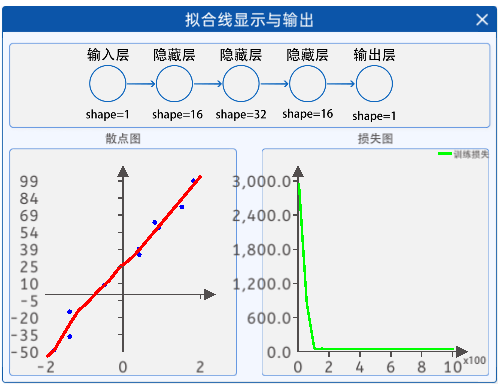
如上图所示，过拟合的状态下，其拟合的曲线想拟合每一个点，这是由于神经网络过度学习了每个点的特征，从而导致拟合的曲线对每个点都非常敏感，影响其拟合的结果。

过拟合的解决方案是比较复杂的，因为正常情况下，欠拟合解决方案比较简单，网络简单，多搞点比较深层次的网络，让网络复杂起来就可以了，数据量太少，多搞点数据。

在过拟合中的数据量太少，多搞点数据，还有一个就是网络太复杂，需要你去弄一个更简单的网络，但是更简单的网络，当网络更简单的时候，代表它的性能不一定是最好的。比如在不断的提出神经网络的时候或者算法的时候，新的算法往往比旧的算法好，不能因为新的算法过拟合，再去使用旧的算法。最优的方式是用新的算法，加一些技巧，让它去拟合你的数据，在你的数据上表现的更好。新的算法不只是网络参数的变多或者层数的变多，它还代表着更加新的技术和更可解释性的一些技巧。

代码

import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt# 1.创造数据，数据集
points = np.array([[-0.5, 7.7], [1.2, 65.8], [0.4, 39.2], [-1.4, -15.7],[1.5, 75.6], [0.4, 34.0], [0.8, 62.3]])
# 分离特征和标签
x_train = points[:, 0]
y_train = points[:, 1]# 2.定义前向模型
class Model(nn.Module):#定义初始化def __init__(self):super(Model,self).__init__()self.layer1=nn.Linear(1,2)# self.layer2=nn.Linear(16,32)# self.layer3=nn.Linear(32,16)self.layer4=nn.Linear(2,1)#前向过程def forward(self,x):#线性层后都跟着激活函数，实现非线性化x=torch.tanh(self.layer1(x))# x=torch.relu(self.layer2(x))# x=torch.relu(self.layer3(x))# 最后一层是拟合回归不用激活x=self.layer4(x)return xmodel=Model()# 3.定义损失函数和优化器
#定义学习率
lr=0.05
#定义损失函数，这里是回归问题用mse
cri=torch.nn.MSELoss()
#定义优化器
optimizer=torch.optim.Adam(model.parameters(),lr=lr)#7.画图
fig,(ax1,ax2) =plt.subplots(1,2,figsize=(12,6))
epoch_list=[]
loss_list=[]
# 4.开始迭代
epoches=1000
for epoch in range(1,epoches+1):#数据转化为tensorx_train_tensor=torch.tensor(x_train,dtype=torch.float32).unsqueeze(1)y_train_tensor=torch.tensor(y_train,dtype=torch.float32)#数据输入模型前向传播pre_result=model(x_train_tensor)#计算损失loss=cri(pre_result.squeeze(1),y_train_tensor)loss_list.append(loss.detach().numpy())epoch_list.append(epoch)#优化更新#梯度清零optimizer.zero_grad()#反向传播loss.backward()#参数更新optimizer.step()# 5.显示频率设置if epoch==1 or epoch%20==0:print(f"epoch:{epoch},loss:{loss}")# 6.绘图ax1.cla()ax1.scatter(x_train,y_train)x_range=torch.tensor(np.linspace(-2,2,100),dtype=torch.float32)y_range=model(x_range.unsqueeze(1))ax1.plot(x_range.detach().numpy(),y_range.detach().numpy().squeeze(1))ax2.cla()ax2.plot(epoch_list,loss_list)plt.pause(1)
plt.show()

实验结果为：