算法题（222）：摆花

审题：

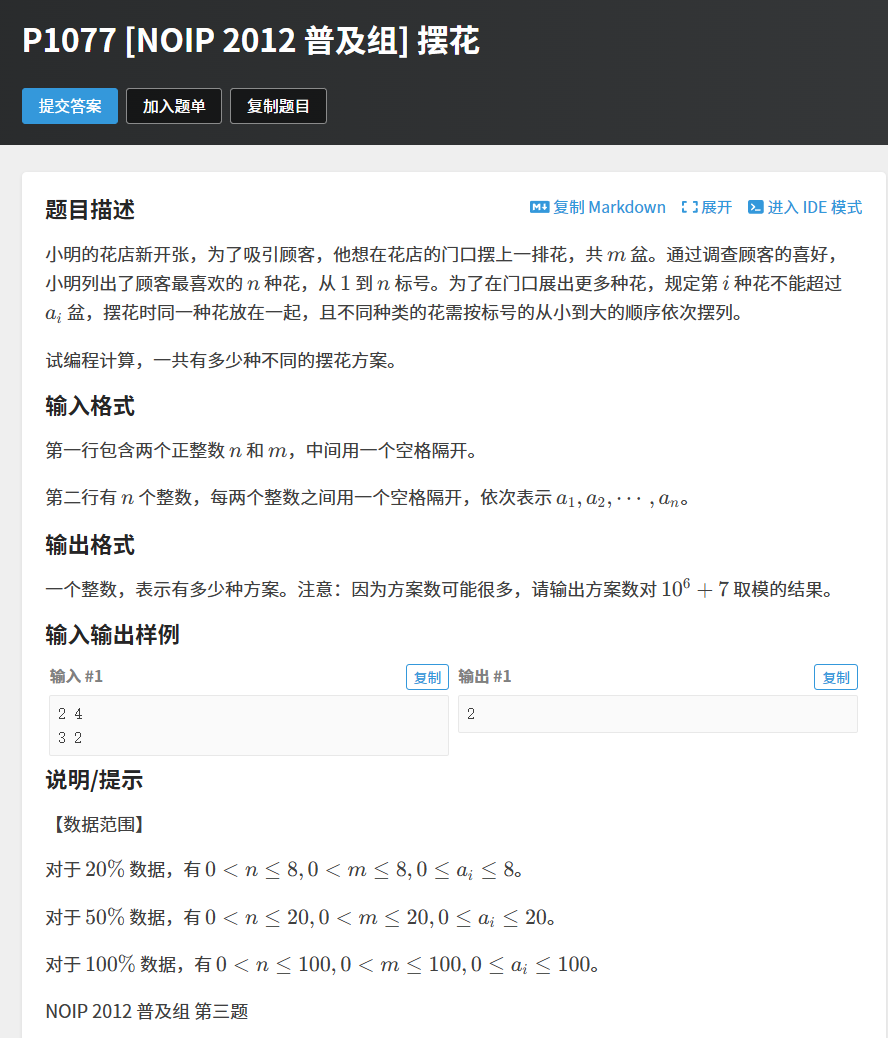
本题需要我们在1~n种有数量限制的花中选取m盆组成一种摆花方案（需要取模1e6+7），且该方案不用考虑排列

思路：

方法一：动态规划

（1）状态表示：

f[i][j]表示在种类1~i范围的花中选择j盆花的所有方案数

（2）状态转移方程：
情况1：不选择i

情况2：选择k个i

其中情况2需要用for循环来计算，且进入for循环计算前一定要满足两个条件

条件1：j >= k，若j小于k说明可选择的盆数j小于想选择的盆数k，非法情况

条件2：k <= a[i]，若k大于a[i]，说明想选择i花的盆数k大于可选择的i花盆数a[i]

（3）初始化：
经过分析，第一行除了（0,0）有一种合法方案，其他位置都是无法达成的，所以要初始化为0，且根据状态转移方程，我们当前节点依赖的都是上一行的节点，所以初始化第一行即可接着计算后面的数据

综上，先全部初始化为0，然后单独将（0,0）赋值为1

（4）填表顺序：
根据状态转移方程，我们纵向从上往下（1~n）遍历即可

（5）答案输出：
直接输出f[n][m]即可

（6）空间优化：
我们本题属于多重背包，且是求方案数的问题，所以只能使用普通的降维，无法进一步使用二进制空间优化

而根据状态转移方程可知，当前节点依赖上一行数据，为了防止数据覆盖，我们需要在横向倒着填表

解题：
空间优化版本

#include<iostream>
using namespace std;
const int N = 110,MOD = 1e6+7;
int n, m;
int a[N], f[N];
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}//初始化f[0] = 1;//填表for (int i = 1; i <= n; i++){for (int j = m; j >= 0; j--){for (int k = 1; k <= min(j, a[i]); k++){f[j] =(f[j]+f[j - k])%MOD;}}}//答案输出cout << f[m] << endl;return 0;}

P1077 [NOIP 2012 普及组] 摆花 - 洛谷