顺序队列与环形队列的基本概述及应用
目录
队列的基本概念介绍
1.队列的基本概念
2.队列的特点
3.类比
队列的顺序存储结构及其基本运算的实现
顺序队列的定义
顺序队中实现队列的基本运算
顺序队的基本运算算法
1)初始化队列 InitQueue
2)销毁队列 DestroyQueue
3)判断队列空 QueueEmpty
4)入队操作 enQueue
5)出队操作 deQueue
队列的环形队列存储结构及其基本运算的实现
相关概念定义
基本实现算法
1. 初始化队列 InitQueue1
2. 销毁队列 DestroyQueue1
3. 判断队列空 QueueEmpty1
4. 入队操作 enQueue1
5. 出队操作 deQueue1
6. 计算元素个数 Count
环形队列的小总结
本文用于给像我一样的初学者学习理解,总结最重要的知识点避免书上杂乱枯燥,也方便自己以及其他老手可借此文进行大体的复习。
队列的基本概念介绍
1.队列的基本概念
队列是一种先进先出(First In First Out, FIFO)的线性数据结构,它只允许在表的一端(称为队尾)进行插入操作,而在另一端(称为队头)进行删除操作。这种特性使得队列中的元素保持其进入的顺序,最先进入的元素最先被处理。以上即是队列的定义了。
2.队列的特点
队列的核心特点是其操作受限性,这意味着不是所有对线性表的操作都可以用于队列。例如,不能直接访问或操作队列中间的元素。这种受限性虽然降低了灵活性,但提高了数据处理的可靠性和可预测性。
-
队头(Front):允许删除的一端,又称队首。在队列中,队头元素是最先被插入的元素,也将是最先被删除的元素。
-
队尾(Rear):允许插入的一端。新元素总是被添加到队尾。
-
空队列:不含任何元素的队列,此时队头和队尾指针重合。
3.类比
为了大家更好的理解,我现在用更加形象的类比来举例:
隧道类比:想象一个单行隧道,车辆从一端进入,从另一端离开。先进入隧道的车辆会先离开,后进入的车辆后离开。这就是队列的FIFO原则。
排队买票:在电影院排队买票时,新来的人排在队伍末尾(入队),买到票的人从队伍前面离开(出队)。如果有人想中途离开(从队列中间删除),这是不允许的,这体现了队列的操作受限性。
以上就是队列的一些最基本的概念,不难理解,队列队列---说白了就是一条队嘛。
队列的基本实现有几种,我们先从顺序结构说起。
队列的顺序存储结构及其基本运算的实现
顺序队列的定义
队列的顺序存储结构是一种利用连续内存空间(通常通过数组实现)来存储队列元素的方法。它通过两个指针(front和 rear)来标记队头和队尾的位置,从而高效地实现“先进先出”(FIFO)的特性。
我们假设队列中的元素个数最多不超过整数MaxSize,所有元素都具有ElemType数据类型,则顺序队类型SqQueue声明如下:
#define ElemType int //我们这里举例就定义为int类型,当然什么类型都可以
#define MaxSize 50 //我们这举例就定义MaxSize为50,填多少都可以
typedef struct
{ElemType data[MaxSize];int front,rear;
}SqQueue; 队列到顺序队的映射过程如图所示:
顺序队中实现队列的基本运算
我们接下来的示意图中MaxSize=5。初始front=rear=-1。图如下:
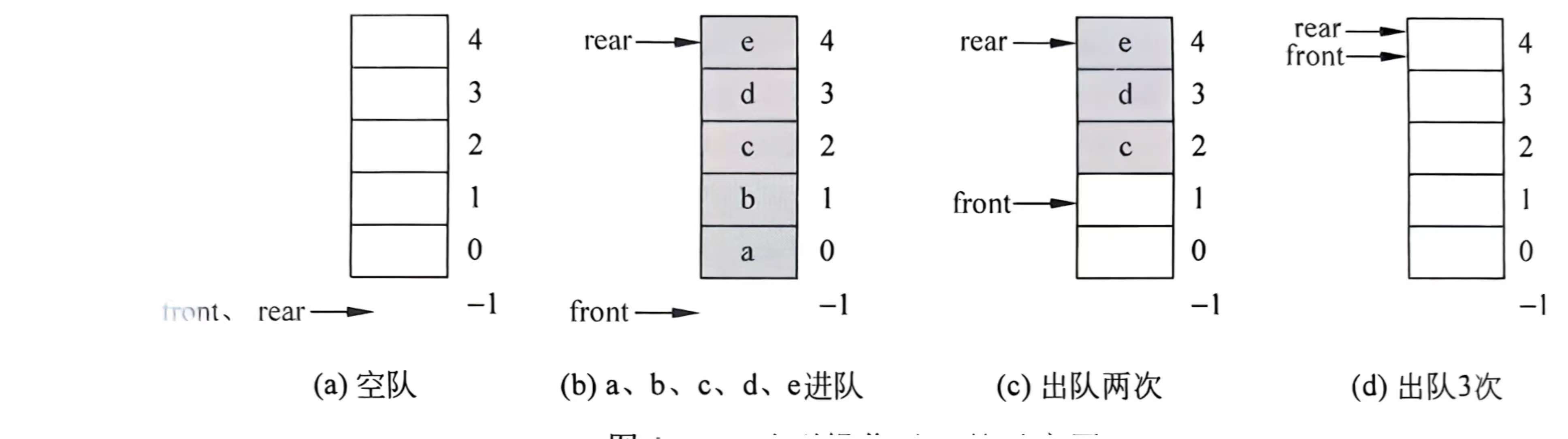
综上所述,对于q所指的顺序队(即顺序队q),初始时设置q->rear=q->front=-1,可以归纳出对后面算法设计来说非常重要的4个要素。
- 队空的条件:q->front==q->rear。
- 队满的条件:q->rear==MaxSize-1(data数组的最大下标)。
- 元素e进队的操作:先将rear增1,然后取出data数组中front位置的元素。
顺序队的基本运算算法
我们先列个表简单概括一下:
| 函数 | 功能描述 | 关键操作 |
|---|---|---|
|
| 初始化队列 | 分配内存, |
|
| 销毁队列 | 释放队列所占内存 |
|
| 判断队列是否为空 | 检查 |
|
| 元素入队 |
|
|
| 元素出队 |
|
1)初始化队列 InitQueue
void InitQueue(SqQueue *&q) {q = (SqQueue *)malloc(sizeof(SqQueue));q->front = q->rear = -1; // 队头和队尾指针初始化为-1
}-
功能:为顺序队列申请内存空间并进行初始化。
-
细节:
-
参数
SqQueue *&q表示一个指向队列指针的引用,允许函数修改调用者传来的指针。 -
初始时将
front和rear都设为 -1。这是一种常见的初始化方式,表示队列为空。
-
-
注意:确保在调用其他队列操作函数前已成功执行此函数。
2)销毁队列 DestroyQueue
void DestroyQueue(SqQueue *&q) {free(q); // 释放队列结构体内存
}功能:释放 malloc为队列分配的内存,防止内存泄漏。
3)判断队列空 QueueEmpty
bool QueueEmpty(SqQueue *q) {return (q->front == q->rear); // 判断队头指针是否等于队尾指针
}-
功能:判断队列是否为空。
-
细节:当
front和rear相等时,队列为空。由于初始化时将它们都设为 -1,且出队入队操作可能使它们相等,此判断在非循环队列且初始化为-1的逻辑下是有效的。 -
重要注意:这种判断方式强烈依赖于初始值设为 -1 以及后续的入队出队操作逻辑。如果初始值不同(如0),此判断法则需调整。
4)入队操作 enQueue
bool enQueue(SqQueue *&q, int e) {if (q->rear == MaxSize - 1) // 判断队尾是否已到数组最大下标return false; // 队满,入队失败q->rear++; // 队尾指针后移q->data[q->rear] = e; // 新元素放入队尾位置return true; // 入队成功
}-
功能:将新元素
e添加到队尾。 -
细节与问题:
-
判满条件:
if (q->rear == MaxSize - 1)检查队尾指针是否已到达数组末端。这是判断队列是否已满的条件。 -
“假溢出”:这是该实现的一个主要问题。即使
q->front不为 -1(即队列前面还有空位),只要rear到达数组末端,就无法再插入新元素,导致假溢出(False Overflow)。例如,经过多次入队和出队后,数组前端可能仍有空闲空间,但rear已到末尾,无法再利用这些空间。 -
操作顺序:先移动
rear指针,再存入数据。
-
5)出队操作 deQueue
bool deQueue(SqQueue *&q, ElemType &e) {if (q->front == q->rear) // 判断队列是否为空return false; // 队空,出队失败q->front++; // 队头指针后移e = q->data[q->front]; // 取出当前队头指针所指元素return true; // 出队成功
}-
功能:删除队头元素并将其值赋给
e。 -
细节与特点:
-
判空条件:使用
if (q->front == q->rear)。 -
front指针的含义:在这段代码中,front指针指向的是队头元素的【前一个位置】。这也是为什么初始化时要设为 -1。-
出队时,先执行
q->front++,使其指向真正的队头元素位置,然后再取出元素e = q->data[q->front]。
-
-
“假溢出”加剧:出队操作仅仅将
front指针后移,原队头位置的内存空间实际上被废弃了。这加剧了前面提到的“假溢出”问题,因为数组前部的空间无法被新入队的元素使用。
-
以上就是顺序队最为重要的基本运算实现了,想必大家看到这些也可以对顺序队有了更加清晰的理解吧
队列的环形队列存储结构及其基本运算的实现
相关概念定义
环形队列的诞生:解决“假溢出”
在你之前提供的顺序队列代码中,存在一个致命问题——“假溢出”(False Overflow)。即当 rear指针移动到数组末尾后,即使数组前端因执行了出队操作而留有空闲空间,也无法再插入新元素,导致空间被浪费。
环形队列(Circular Queue)的诞生正是为了解决这个问题。它通过将线性数组在逻辑上首尾相连,形成一个环(Circle),使得当指针移动到数组末尾时,可以通过取模运算(Modulo Operation)让它“绕回”数组开头,从而循环利用之前出队所释放的空间。
这种设计巧妙地规避了假溢出,极大地提高了固定空间的使用效率,特别适合处理数据流、缓冲等场景。
说白了就是将它的逻辑结构变成一个环形,但是它的物理结构依然是类似一个普通的线性数组。
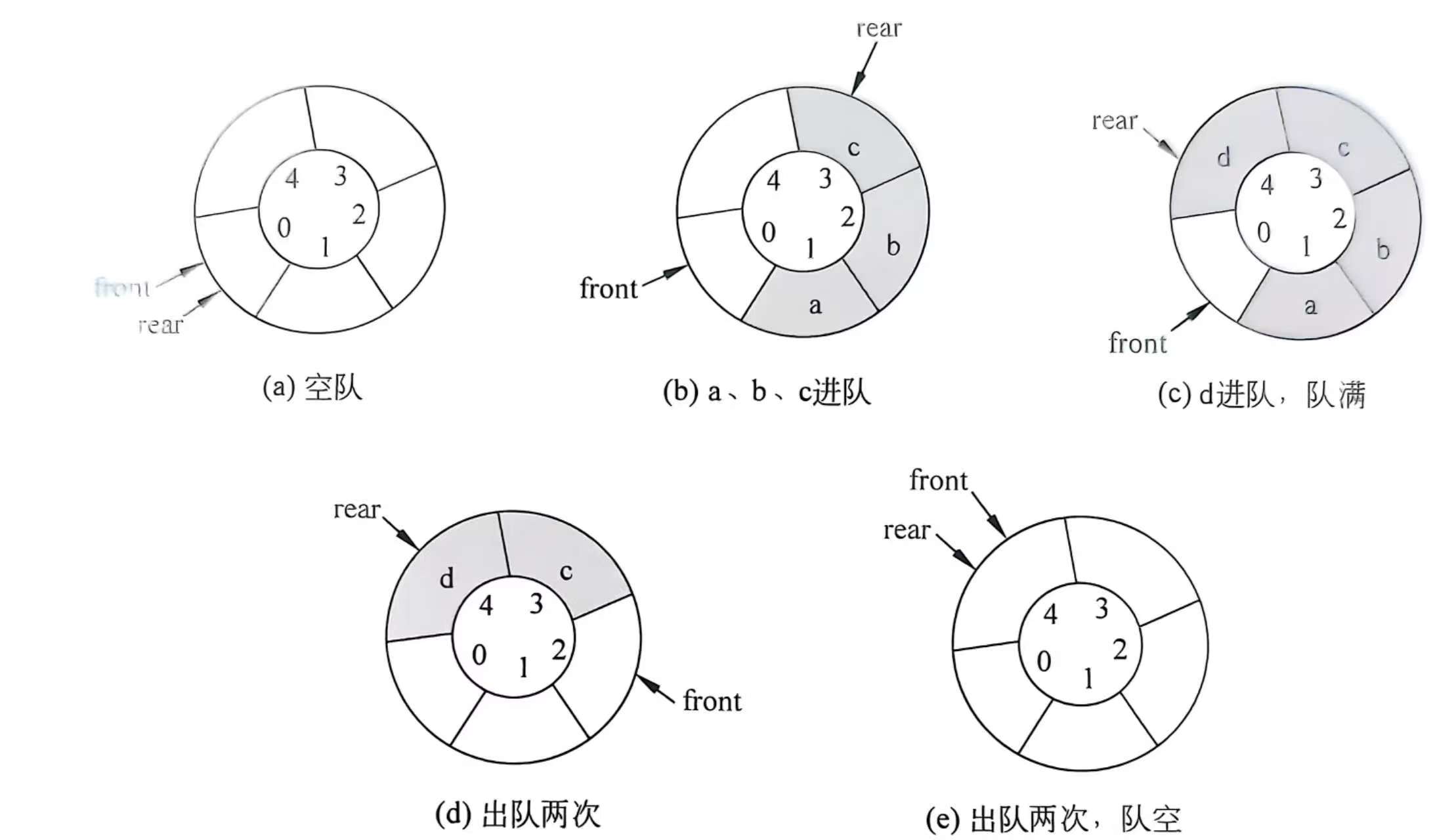
环形队列首尾相连之后头指针front和尾指针rear增1就不同于顺序队列了。而是如下算法:
front=(front+1)%MaxSize
rear=(rear+1)%MaxSize由于要循环,所以还要余个MaxSize。如有不理解在后面会有示意图帮助你理解的。
环形队列的队空条件是q->rear==q->front。当进队元素的速度快于出队元素的速度时,就会赶上队首指针,那么就会使队满也是q->rear==q->front,就会造成无法区分队空和队满。这显然是不对的。所以我们要改为“队尾指针循环增1时等于队头指针”作为队满条件。这样环形队列就会少用一个元素空间,即该队列中在任何时候就只能存储最多MaxSize-1个元素。
因此,在环形队列q中设置
- 队空条件是q->rear==q->front。
- 队满条件是(q->rear+1)%MaxSize==q->front。
- 出队和进队操作改为分别将队尾rear和队头front循环+1。
下图说明了环形队列操作的几种状态,设MaxSize为5。
基本实现算法
1. 初始化队列 InitQueue1
void InitQueue1(SqQueue *&q) {q = (SqQueue *)malloc(sizeof(SqQueue));q->front = q->rear = 0; // 队头和队尾指针初始化为0
}-
功能:为环形队列申请内存空间并进行初始化。
-
细节:
-
参数
SqQueue *&q是一个引用参数,允许函数修改调用者传来的指针。 -
初始时将
front和rear都设为 0。这是环形队列最常见的初始化方式。
-
-
注意:确保在调用其他队列操作函数前已成功执行此函数。
2. 销毁队列 DestroyQueue1
void DestroyQueue1(SqQueue *&q) {free(q); // 释放队列结构体内存
}-
功能:释放
malloc为队列分配的内存,防止内存泄漏。 -
注意:此函数释放了队列结构体的内存,但假设
q->data是结构体内部的静态数组(如ElemType data[MaxSize]),所以无需单独释放。如果data是动态分配的指针,则需要先释放q->data再释放q。此外,更安全的做法是在释放后将指针q置为NULL,但这里没有体现。
3. 判断队列空 QueueEmpty1
bool QueueEmpty1(SqQueue *q) {return (q->rear == q->front); // 判断队头指针是否等于队尾指针
}-
功能:判断队列是否为空。
-
细节:当
front和rear相等时,队列为空。这是环形队列判断队空的基本条件。
4. 入队操作 enQueue1
bool enQueue1(SqQueue *&q, int e) {if ((q->rear + 1) % MaxSize == q->front) // 判断队满return false; // 队满,入队失败q->rear = (q->rear + 1) % MaxSize; // 队尾指针循环后移q->data[q->rear] = e; // 新元素放入当前队尾位置return true; // 入队成功
}-
功能:将新元素
e添加到队尾。 -
细节与原理:
-
判满条件:
。当队尾指针的下一个位置是队头时,就认为队列已满。这样做的目的是为了区分队空和队满(因为两者在表面上都是if ((q->rear + 1) % MaxSize == q->front)。此条件是“牺牲一个存储单元”法的核心front == rear)。因此,这个队列最多可存储MaxSize - 1个元素。 -
操作顺序:先移动指针,再存入数据。这是一个非常关键的特点。
rear指针始终指向最后一个有效元素的下一个空位(或者说,当前队尾位置可以放入新元素)。 -
循环:通过取模运算
% MaxSize实现指针的循环移动。当rear指向数组末尾时(MaxSize-1),再加一取模就会回到数组开头(0)。
-
5. 出队操作 deQueue1
bool deQueue1(SqQueue *&q, int &e) {if (q->rear == q->front) // 判断队空return false; // 队空,出队失败q->front = (q->front + 1) % MaxSize; // 队头指针循环后移e = q->data[q->front]; // 取出当前队头指针所指元素return true; // 出队成功
}-
功能:删除队头元素并将其值赋给
e。 -
细节与原理:
-
判空条件:
if (q->rear == q->front)。 -
front指针的含义:在这段代码中,front指针指向的是队头元素的【前一个位置】。这也是为什么出队时,需要先执行q->front = (q->front + 1) % MaxSize;使其指向真正的队头元素位置,然后再取出元素e = q->data[q->front];。 -
操作顺序:先移动指针,再取出数据。与入队操作顺序一致。
-
循环:同样通过取模运算实现循环。
-
6. 计算元素个数 Count
int Count(SqQueue *q) {return ((q->rear - q->front + MaxSize) % MaxSize);
}-
功能:计算队列中当前有多少个元素。
-
细节与原理:
-
公式
(rear - front + MaxSize) % MaxSize是计算环形队列元素个数的标准方法。 -
+ MaxSize:是为了防止rear - front出现负数,确保被除数始终为正。 -
% MaxSize:最后取模是为了将结果映射到0到MaxSize-1的范围内。 -
例如,若
MaxSize=5,front=2,rear=0,计算过程:(0-2+5) % 5 = 3 % 5 = 3。这表示队列中有3个元素。
-
环形队列的小总结
-
“牺牲一个单元”策略:这是该实现最核心的特点。通过故意浪费一个存储单元,巧妙地解决了队空和队满的判断条件冲突问题(否则当队列真满时,
front也会等于rear,无法与队空区分)。因此,队列的实际容量是MaxSize - 1。 -
指针的指向
-
front:指向队头元素的前一个位置。 -
rear:指向队尾元素的下一个空位。 -
这种指向约定使得入队和出队操作都遵循“先移动指针,再操作数据”的统一顺序。
-
-
循环的实现:通过取模运算
% MaxSize让指针在数组的物理边界上实现“循环”,这是环形队列的灵魂。它使得队列可以重复利用出队后释放的空间,克服了普通顺序队列的“假溢出”问题。 -
操作顺序:无论是入队还是出队,都是先移动指针,再操作数据。这一点需要牢记,它与指针的初始定义是自洽的。
总的来说队列的顺序结构和环形结构就是以上的基本内容。在本文我没有举例相关应用,因为再举就篇幅太长,起码搞一万字了,在这就不举应用题了,希望本文可以帮助到大家理解队列的两个基本结构。
