数据结构入门 (五)：约束即是力量 —— 深入理解栈

引言：线性表的“受限模式”

在之前的探索中，我们已经熟悉了线性表——一种元素和元素“手拉手”的队伍。在这种结构中，我们可以在任意位置进行插入和删除，非常自由。

但须知，过度的自由也意味着混乱，越没有约束的结构也越没有意义，而表就是约束最少的有意义的数据结构。在许多现实场景中，我们需要的是一种更具纪律性、行为更可预测的结构。

我们在线性表上给它添加一个简单的约束：所有插入和删除操作，都只能在表的同一端进行。这个看似简单的“自我束缚”，却催生了一种极其强大而又应用广泛的数据结构——栈。

我们把允许插入和删除的一端称栈顶，另一端称为栈底。栈底是固定的，最先进栈的只能在栈底。栈的插入操作，叫做进栈；栈的删除操作，叫做出栈。

图1 进栈出栈示意图

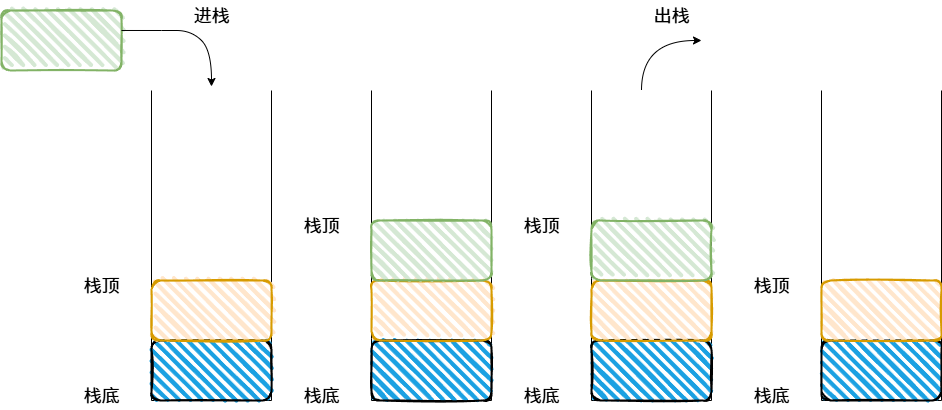
栈的核心特性是后进先出(Last-In, First-Out, LIFO)。这个特性让它非常普遍地被应用。比如实现“撤销/重做”功能、记录函数调用轨迹（调用栈）和深度优先搜索等。

一、顺序栈：数组的"后进先出"艺术

栈作为一类特殊的线性表，自然可以用数组来实现。这种基于顺序存储的栈，我们称之为顺序栈。

那么对于顺序栈来说数组的哪一端是栈顶，哪一端是栈底？显然数组里下标为0的一端作为固定的栈底比较好。同时我们需要一个游标top是时刻追踪栈顶元素在数组中的位置。

栈的设计模式

在书写顺序栈之前，我们需要了解四个概念：满栈，空栈，递增栈，递减栈。

1.栈的两种状态

栈的状态由栈顶指针 top 的位置决定，它决定了如何判断栈是否为空或已满。

空栈指的是top指针指向下一次要入栈的位置。当栈为空时，下一个插入位置是 0，因此 top == 0。

满栈指的是top指针指向最后压入的数据。若存储栈的最大容量为MaxSize，栈顶位置top必须小于MaxSize，满栈的判定条件为top = MaxSize - 1。

2.栈的两种增长方向

递增栈指的是栈的内存空间从低地址向高地址扩展，随着元素入栈，栈顶指针 top 的值递增。

递减栈指的是栈的内存空间从高地址向低地址扩展,随着元素入栈，栈顶指针 top 的值递减。

将上述状态和方向两两结合，这样会有四个组合：递增满栈，递增空栈，递减满栈，递减空栈。

图2 四种组合

递增空栈：

// 压栈
a1.data[a1.pos] = 1;//先赋值
a1.pos++;//后移动pos位置// 出栈
x = a1.data[a1.pos];
a1.pos--

递增满栈：

pos++;//先更新pos指向位置
a1.data[a1.pos]=1;//再赋值

递减空栈：

a1.data[a1.pos]=e;//先赋值
pos--;//后更新位点

递减满栈：

// 压栈
pos--;//先更新指向
a1.data[a1.pos]=e;//后更新栈值
// 出栈

二、顺序栈的C语言实现

1.定义结构体与接口

#define MaxStackSize 5
typedef int Element;
typedef struct
{Element data[MaxStackSize];int top;
} ArrayStack;// 递增空栈
void initArrayStack(ArrayStack *stack);void pushArrayStack(ArrayStack *stack, Element e);
void popArrayStack(ArrayStack *stack);Element getTopArrayStack(const ArrayStack *stack);int isEmptyArrayStack(const ArrayStack *stack);
int isFullArrayStack(const ArrayStack *stack);

2.初始化栈

// 递增空栈
void initArrayStack(ArrayStack* stack)
{memset(stack->data, 0, sizeof(stack->data));stack->top = 0;
}

3.压栈

void pushArrayStack(ArrayStack *stack, Element e)
{stack->data[stack->top] = e;++stack->top;
}

4.弹栈

void popArrayStack(ArrayStack *stack)
{--stack->top;
}

5.查询

Element getTopArrayStack(const ArrayStack *stack)
{int pos = stack->top - 1;return stack->data[pos];
}

6.判断是否为空栈

int isEmptyArrayStack(const ArrayStack *stack)
{return stack->top == 0;
}

7.判断是否为满栈

int isFullArrayStack(const ArrayStack *stack)
{return stack->top == MaxStackSize;
}

8.测试函数

#include "arrayStack.h"
#include <stdio.h>void test01()
{ArrayStack info;initArrayStack(&info);for (int i = 0; i < 5; i++){pushArrayStack(&info, i + 100);}printf("push 5 element success!\n");if (!isFullArrayStack(&info)){pushArrayStack(&info, 500);}// 采用弹栈，弹一个看一个，直到弹完为止Element w;printf("show:");while (!isEmptyArrayStack(&info)){w = getTopArrayStack(&info);printf("\t%d",w);popArrayStack(&info);}printf("\n");
}int main()
{test01();
}

结果为：

三、链式栈：永不“溢出”的自由

与顺序表相同，面对不知道数量的元素时，使用顺序栈可能造成“溢出”。为了追求灵活性，这时候就需要用到栈的链式存储结构——链式栈。

栈顶是做插入删除操作的，那么栈顶应该放在链表的头部还是尾部呢？我们知道，单链表必然有头指针，而栈顶指针是必须的，那么干脆让它们合体好了，同时对头部的插入和删除都是 O(1) 操作。所以一般把链表的头部作为栈顶。同时由于栈顶已经在头部了，单链表的头节点也失去意义了，对于链式栈来说，不需要头节点。

插入操作：

new_node->next = top;
top = new_node;

删除：

tmp = top;
top = top->next;
free(tmp);

四、链式栈的C语言实现

1.定义结构体与接口

#include "common.h"typedef struct _node
{Element data;struct _node *next;
} StackNode;typedef struct
{StackNode *top;int count;
} LinkStack;LinkStack *createLinkStack();
void releaseLinkStack(LinkStack *stack);int pushLinkStack(LinkStack *stack, Element e);
int popLinkStack(LinkStack *stack, Element *e);

2.创建链式栈

LinkStack *createLinkStack()
{LinkStack* link_stack = malloc(sizeof(LinkStack));if (link_stack == NULL){fprintf(stderr, "LinkStack malloc failed\n");return NULL;}link_stack->top = NULL;link_stack->count = 0;return link_stack;
}

3.压栈

int pushLinkStack(LinkStack *stack, Element e)
{StackNode* node = malloc(sizeof(StackNode));if (node == NULL){fprintf(stderr, "Stack Node malloc failed\n");return -1;}node->data = e;node->next = stack->top;;stack->top = node;++stack->count;return 0;
}

4.弹栈

int popLinkStack(LinkStack* stack, Element* e)
{if (stack->top == NULL){fprintf(stderr, "stack empty!\n");return -1;}*e = stack->top->data;StackNode *tmp = stack->top;stack->top = tmp->next;free(tmp);--stack->count;return 0;
}

5.释放

void releaseLinkStack(LinkStack *stack)
{if (stack){while (stack->top){StackNode *tmp = stack->top;stack->top = tmp->next;free(tmp);--stack->count;}printf("stack count:%d\n", stack->count);}
}

6.测试函数

void test02()
{LinkStack *stack = createLinkStack();if (stack == NULL){return;}for (int i = 0; i < 5; i++){pushLinkStack(stack, i + 50);}printf("Have %d element on thr stack!\n", stack->count);Element w;while (popLinkStack(stack, &w) != -1){printf("\t%d", w);}printf("\n");releaseLinkStack(stack);
}int main()
{test02();
}

结果为：

五、总结：效率与灵活性的抉择

今天，我们学习了栈——一种通过施加“约束”而获得强大力量的数据结构。在实现上，我们有两种主流选择：

特性	顺序栈 (动态数组)	链式栈
空间使用	内存连续，缓存友好。可能有预留空间造成浪费。	按需分配，无空间浪费，但有指针额外开销。
容量	有容量上限，需要扩容，扩容有性能代价。	理论上无容量上限，受限于系统总内存。
性能	通常更快，因为数组的内存局部性对CPU缓存有利。	每次操作都涉及 malloc/free，开销相对较大。
适用场景	元素数量可预估，对性能要求高的场景。	元素数量极不确定，或可能非常深的递归场景。

总的来说，顺序栈性能高，但容量有限；而链式栈则无限容量，灵活但取用稍慢。

我们已经掌握了“后进先出”的栈，那么它的兄弟——“先进先出”的公平排队模型，又该如何设计呢？这就是我们下一篇文章的主题：队列。