Python14-SVM⽀持向量机
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 1. 介绍
- 2. SVM算法api初步使⽤
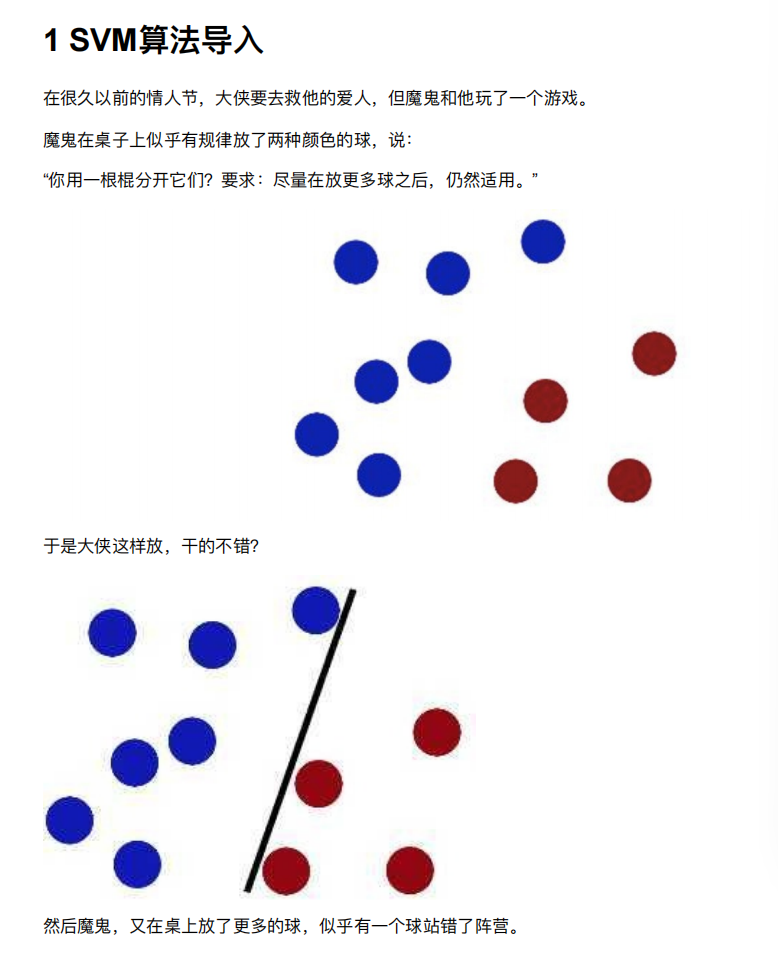
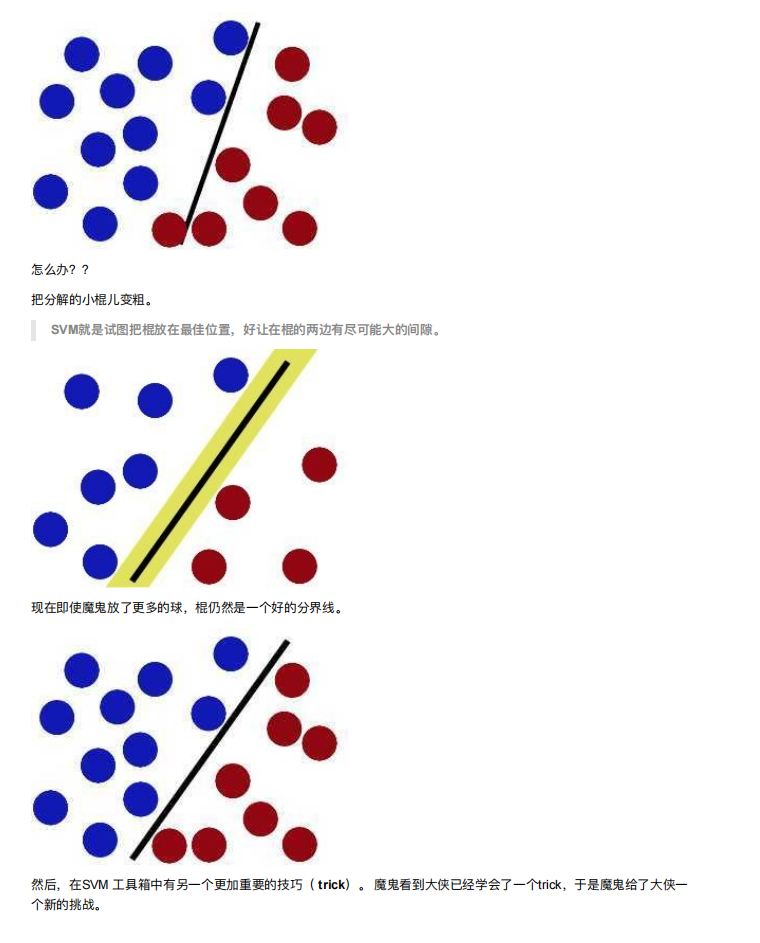
- 3. SVM算法原理
- 4. SVM损失函数
- 5. SVM的核⽅法
- 6. SVM回归
- 7. SVM算法api再介绍
- 7.1 SVC
- 7.2 NuSVC
- 7.3 LinearSVC
- 8. 案例:数字识别器
- 总结
前言
1. 介绍

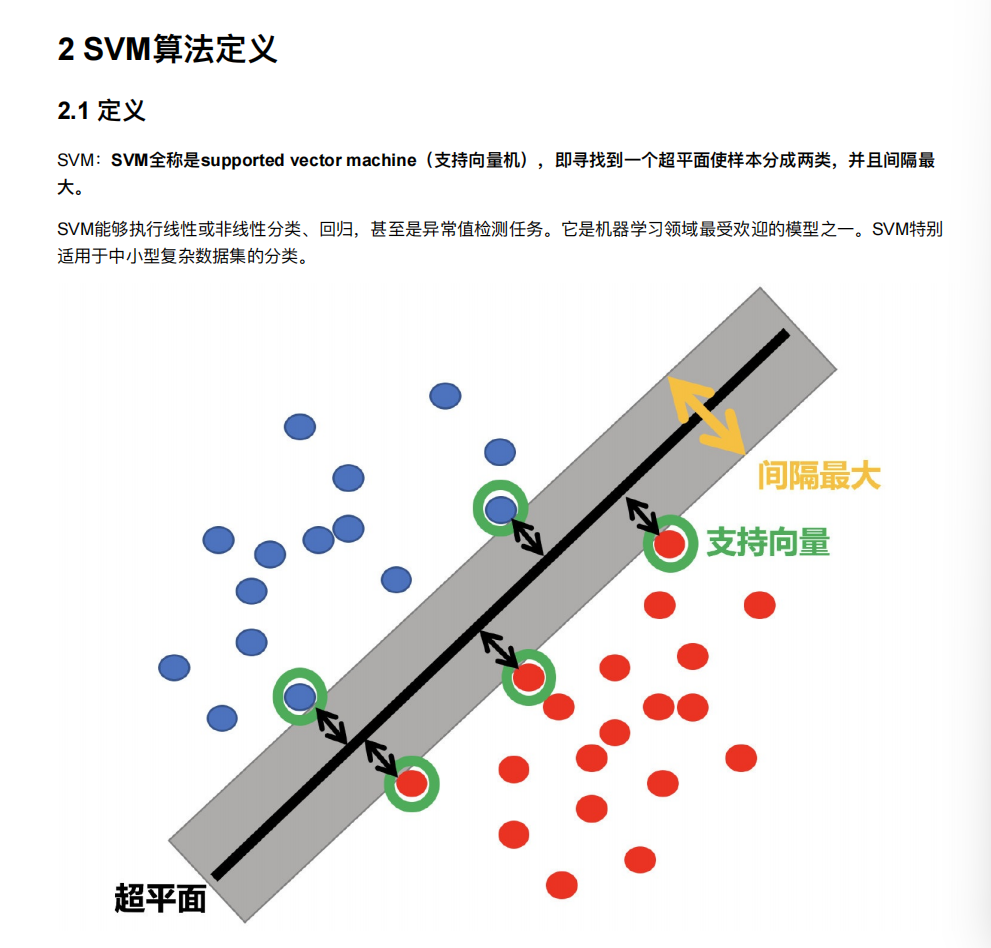
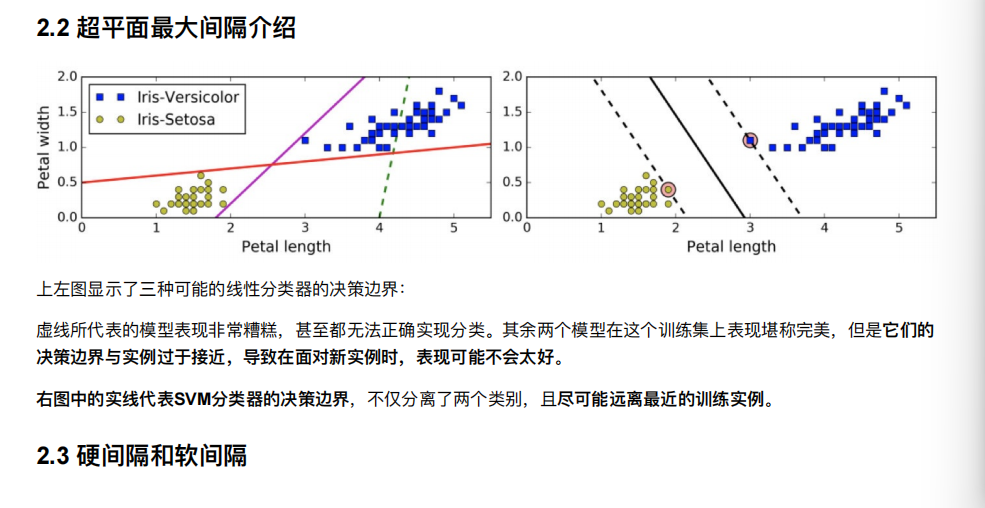
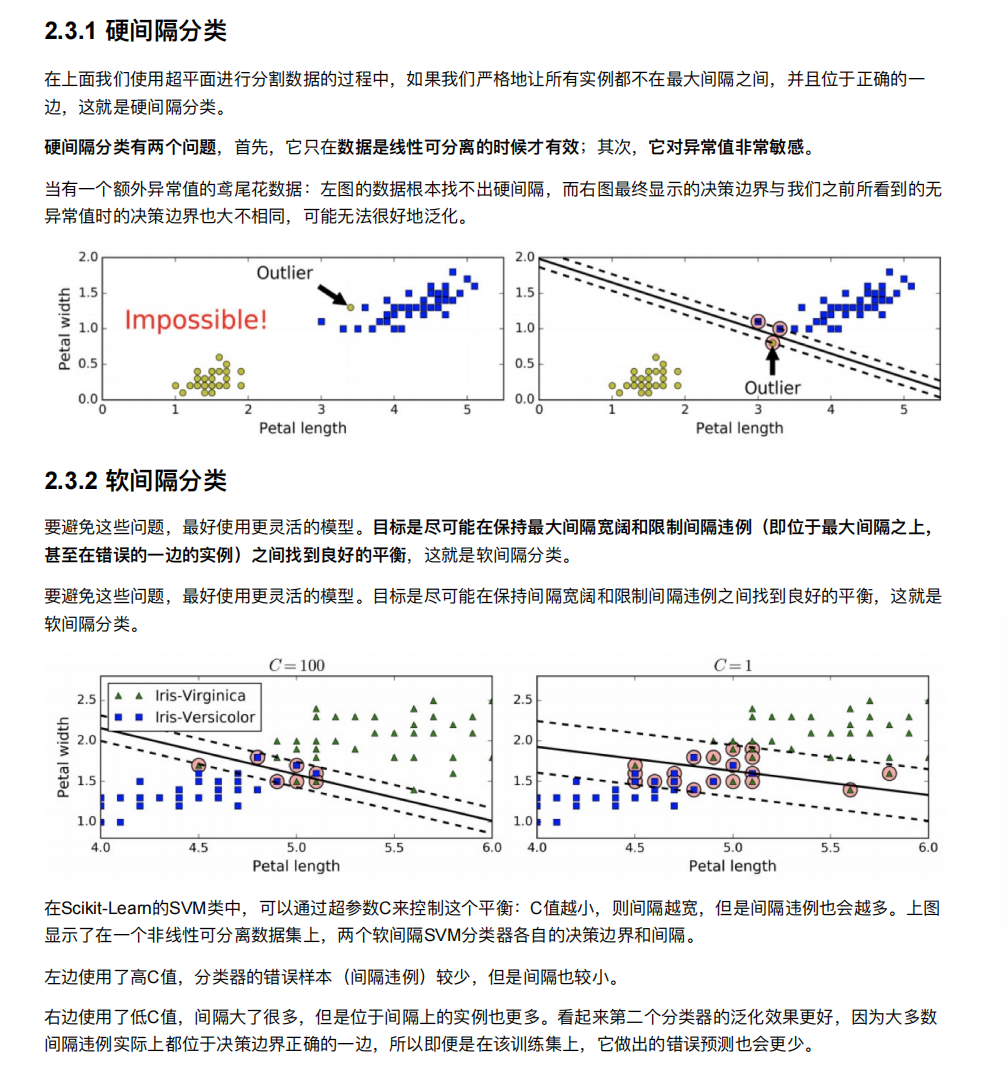
2. SVM算法api初步使⽤
from sklearn import svm
x=[[0,0],[1,1]]
y=[0,1]
ss=svm.SVC()
ss.fit(x,y)
ss.predict([[2,2]])
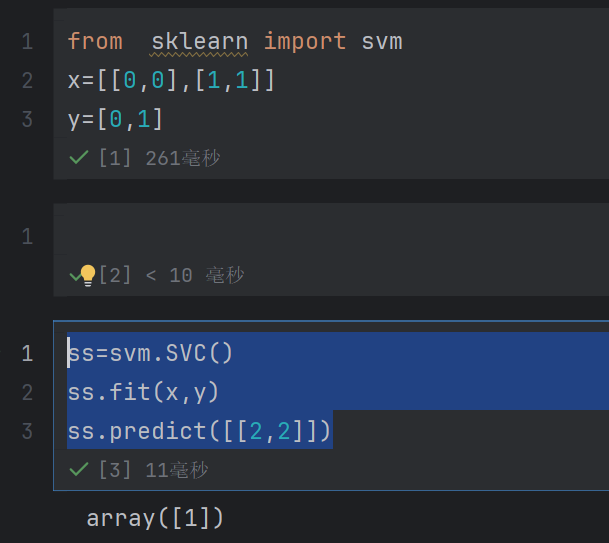
3. SVM算法原理



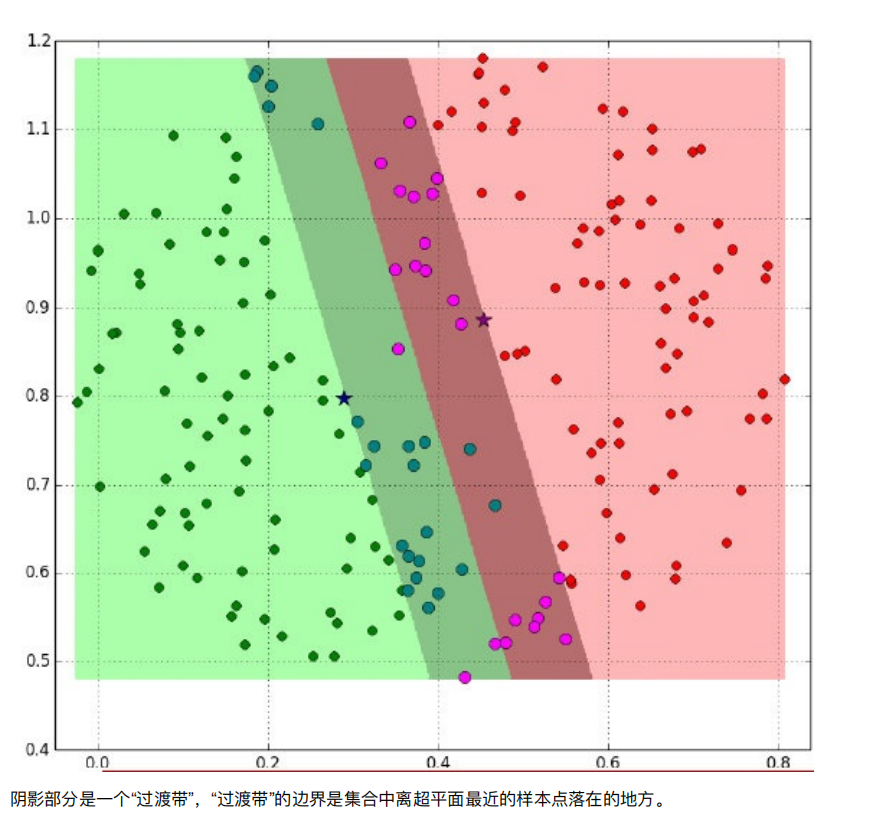





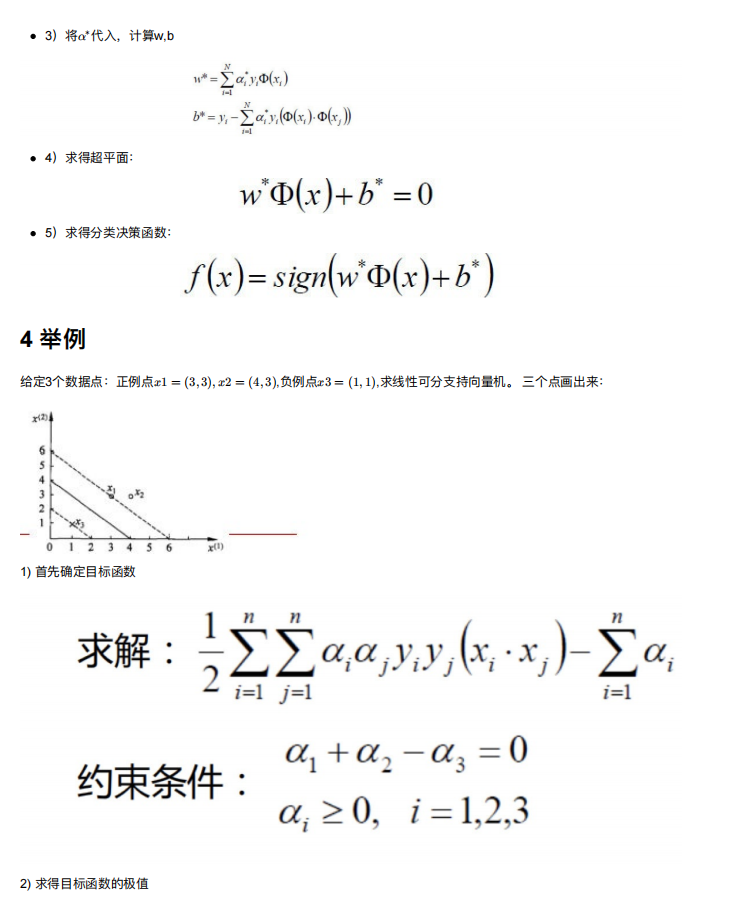


4. SVM损失函数
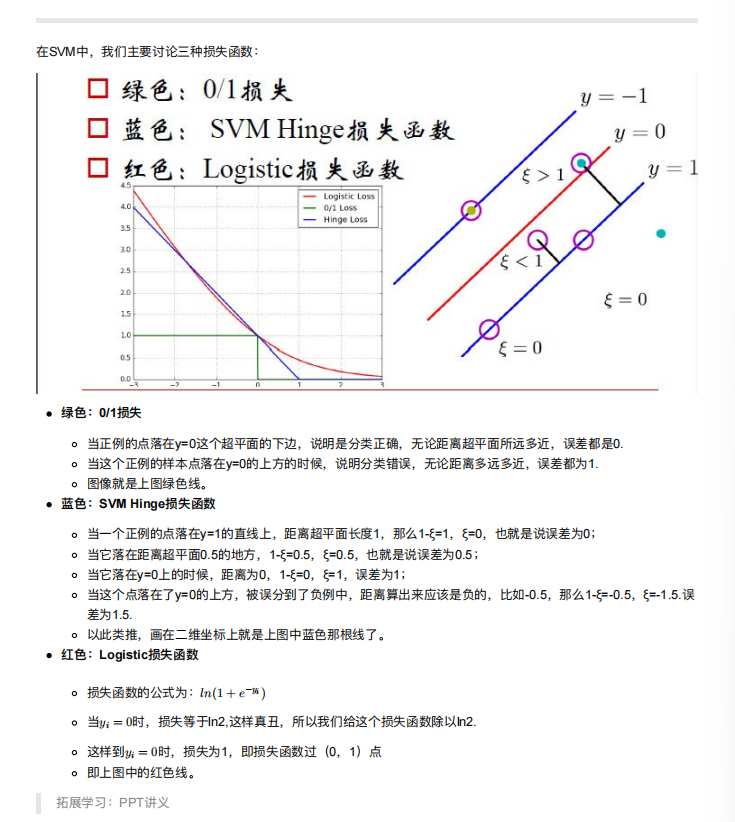
主要用的是Hinge损失
5. SVM的核⽅法
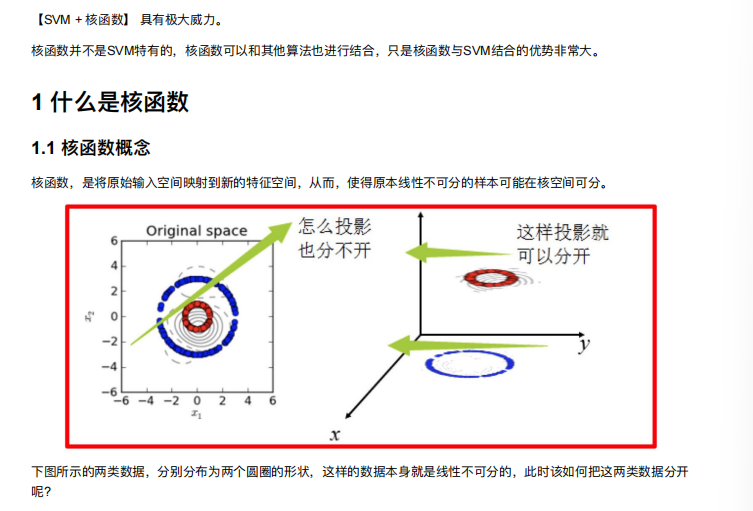
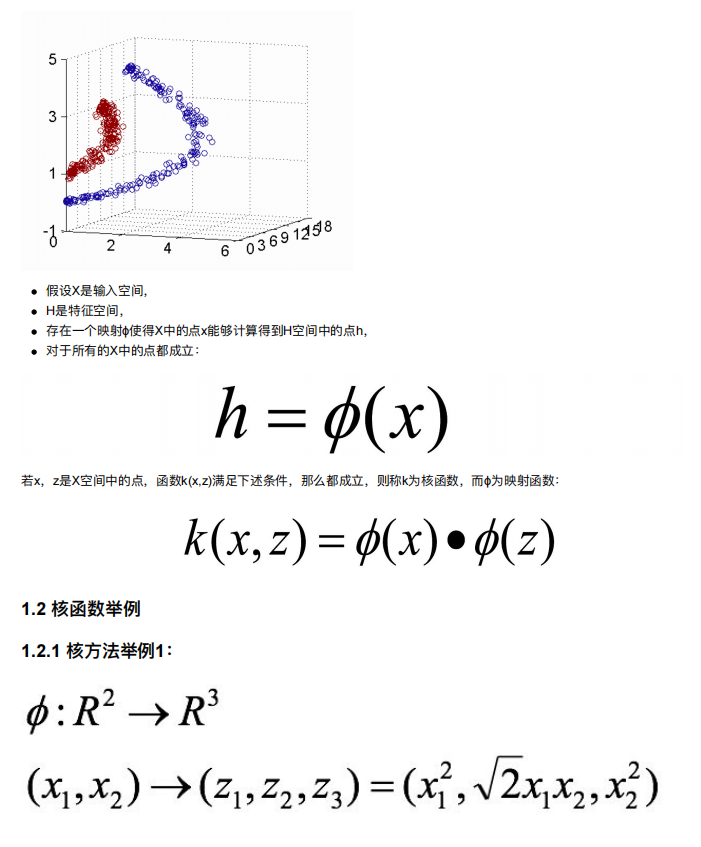
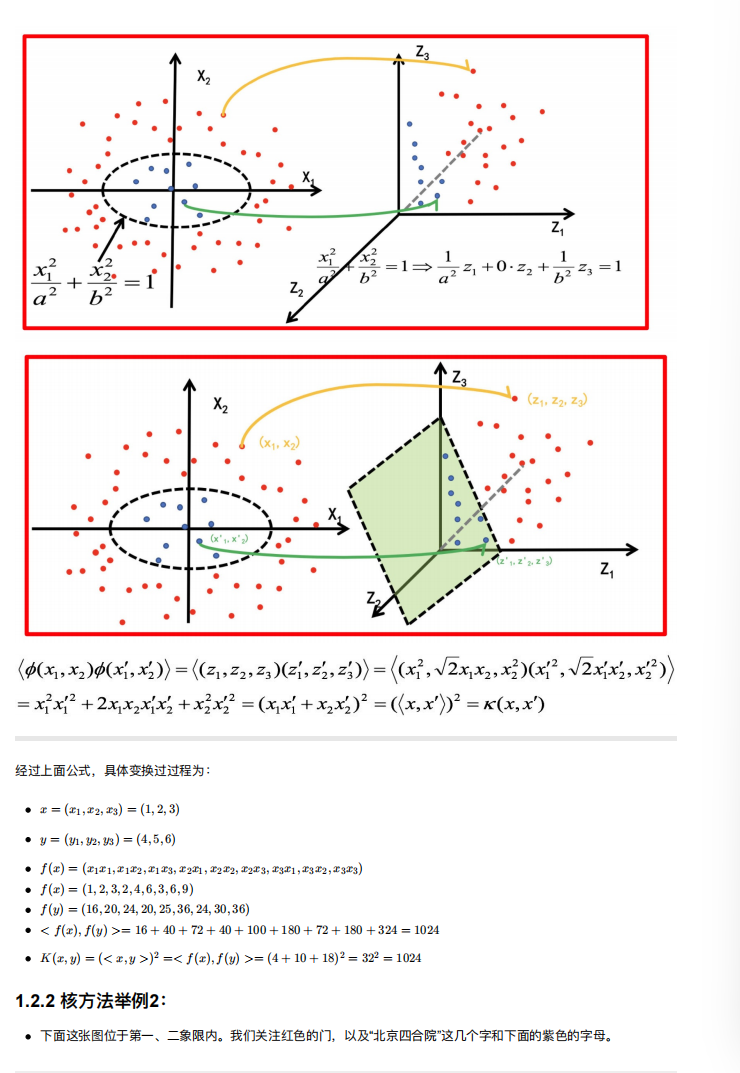



一般使用RBF高斯核
6. SVM回归
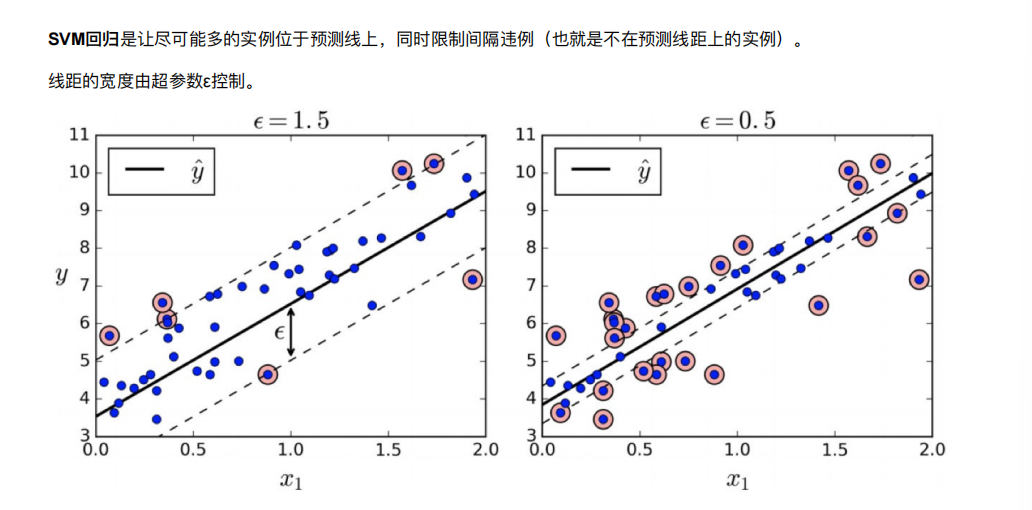
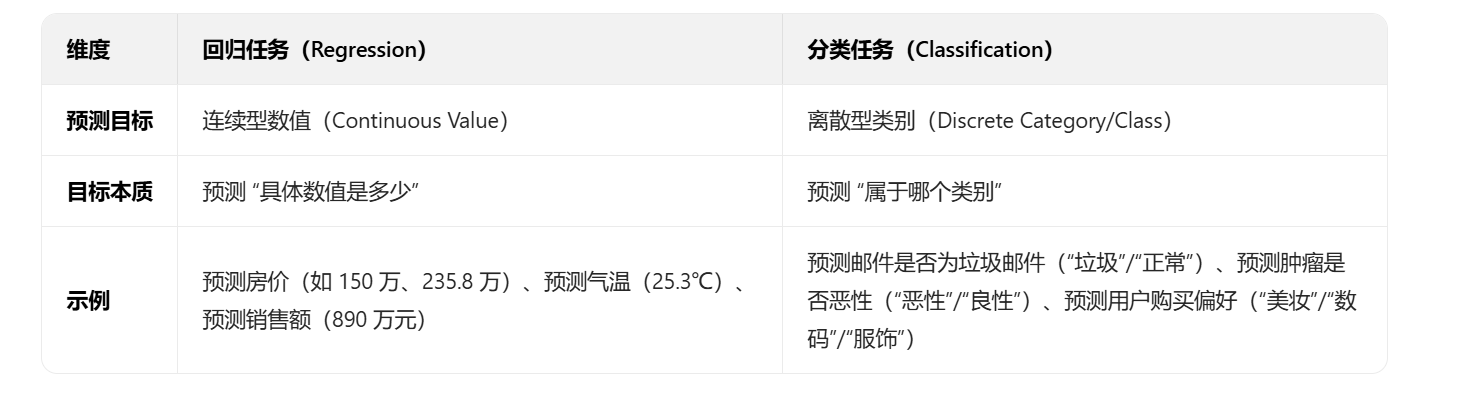
回归任务的目标是预测连续型数值,也就是可以取某一区间内任意具体数值的变量。简单说,回归要回答的是 “具体是多少” 的问题。比如预测一套房子的成交价(可能是 156.8 万、230.5 万等任意数值)、明天的气温(22.3℃、25.1℃)、下个月的销售额(890 万、1020 万),这些目标都不是固定的 “类别”,而是可连续变化的数值。
分类任务的目标是预测离散型类别,也就是目标变量只能从预设的几个固定选项中选一个。简单说,分类要回答的是 “属于哪一类” 的问题。比如判断一封邮件是 “垃圾邮件” 还是 “正常邮件”、诊断肿瘤是 “恶性” 还是 “良性”、预测用户会点击 “美妆类”“数码类” 还是 “服饰类” 商品,这些目标都是明确且互斥的 “类别”,无法取类别之外的中间值
7. SVM算法api再介绍
SVM⽅法既可以⽤于分类(⼆/多分类),也可⽤于回归和异常值检测。
SVM具有良好的鲁棒性,对未知数据拥有很强的泛化能⼒,特别是在数据量较少的情况下,相较其他传统机器学习
算法具有更优的性能。
使⽤SVM作为模型时,通常采⽤如下流程:
- 对样本数据进⾏归⼀化
- 应⽤核函数对样本进⾏映射(最常采⽤和核函数是RBF和Linear,在样本线性可分时,Linear效果要⽐RBF好)
- ⽤cross-validation和grid-search对超参数进⾏优选(交叉验证,网格搜索)
- ⽤最优参数训练得到模型
- 测试
sklearn中⽀持向量分类主要有三种⽅法:SVC、NuSVC、LinearSVC,扩展为三个⽀持向量回归⽅法:SVR、
NuSVR、LinearSVR。
SVC和NuSVC⽅法基本⼀致,唯⼀区别就是损失函数的度量⽅式不同
NuSVC中的nu参数和SVC中的C参数;
LinearSVC是实现线性核函数的⽀持向量分类,没有kernel参数
7.1 SVC
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3,coef0=0.0,random_state=None)
C: 惩罚系数,⽤来控制损失函数的惩罚系数,类似于线性回归中的正则化系数。C越⼤,相当于惩罚松弛变量,希望松弛变量接近0,即对误分类的惩罚增⼤,趋向于对训练集全分对的情况,这样会出现训练集测试时准确率很⾼,但泛化能⼒弱,容易导致过拟合。C值⼩,对误分类的惩罚减⼩,容错能⼒增强,泛化能⼒较强,但也可能⽋拟合。
kernel: 算法中采⽤的核函数类型,核函数是⽤来将⾮线性问题转化为线性问题的⼀种⽅法。参数选择有RBF, Linear, Poly, Sigmoid或者⾃定义⼀个核函数。默认的是"RBF",即径向基核,也就是⾼斯核函数;⽽Linear指的是线性核函数,Poly指的是多项式核,Sigmoid指的是双曲正切函数tanh核;。
degree:当指定kernel为'poly'时,表示选择的多项式的最⾼次数,默认为三次多项式;若指定kernel不是'poly',则忽略,即该参数只对'poly'有⽤。多项式核函数是将低维的输⼊空间映射到⾼维的特征空间。
coef0: 核函数常数值(y=kx+b中的b值),只有‘poly’和‘sigmoid’核函数有,默认值是0。
7.2 NuSVC
class sklearn.svm.NuSVC(nu=0.5)
nu: 训练误差部分的上限和⽀持向量部分的下限,取值在(0,1)之间,默认是0.5
7.3 LinearSVC
线性核函数
class sklearn.svm.LinearSVC(penalty='l2', loss='squared_hinge', dual=True, C=1.0)
penalty:正则化参数,L1和L2两种参数可选,仅LinearSVC有。
loss:损失函数,有hinge和squared_hinge两种可选,前者⼜称L1损失,后者称为L2损失,默认是squared_hinge,其中hinge是SVM的标准损失,squared_hinge是hinge的平⽅
dual:是否转化为对偶问题求解,默认是True。
C:惩罚系数,⽤来控制损失函数的惩罚系数,类似于线性回归中的正则化系数
8. 案例:数字识别器


import pandas as pd
import numpy as np
import matplotlib.pyplot as pltfrom sklearn import svm
from sklearn.model_selection import train_test_split
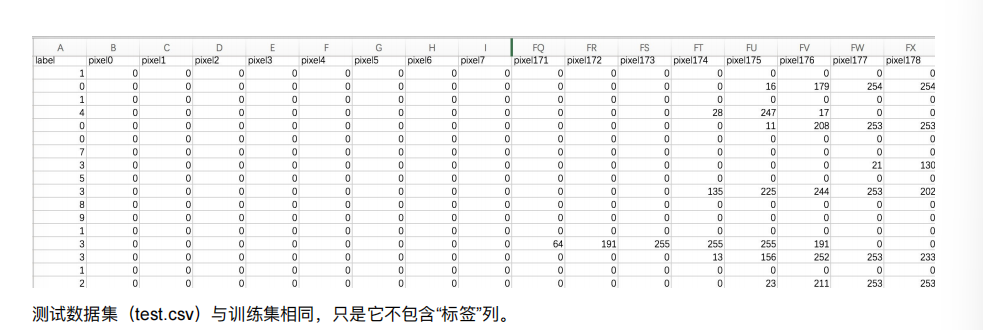
#获取数据
train = pd.read_csv('./source/train2.csv')
train
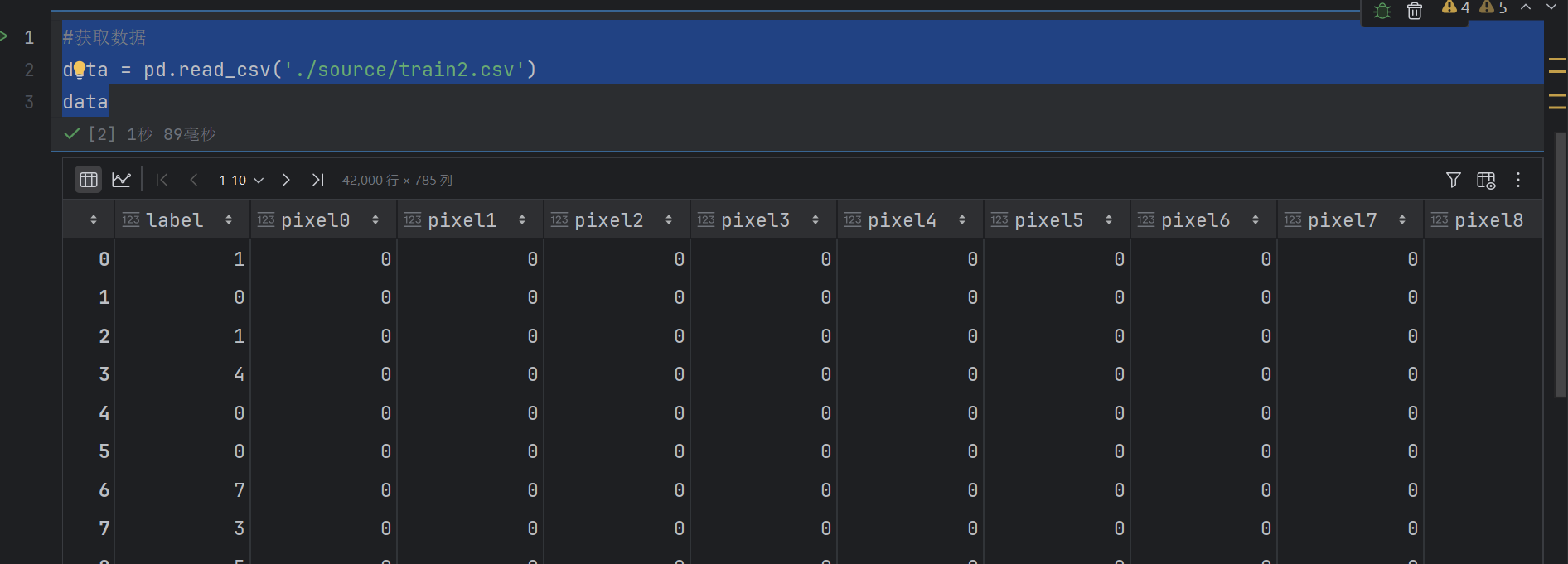
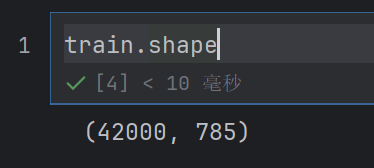
700多个特征—》降维
train_image=train.iloc[:,1:]
这个就是特征值
train_label=train.iloc[:,0]
这个是目标值
#查看具体图像
train_image.iloc[0,].values
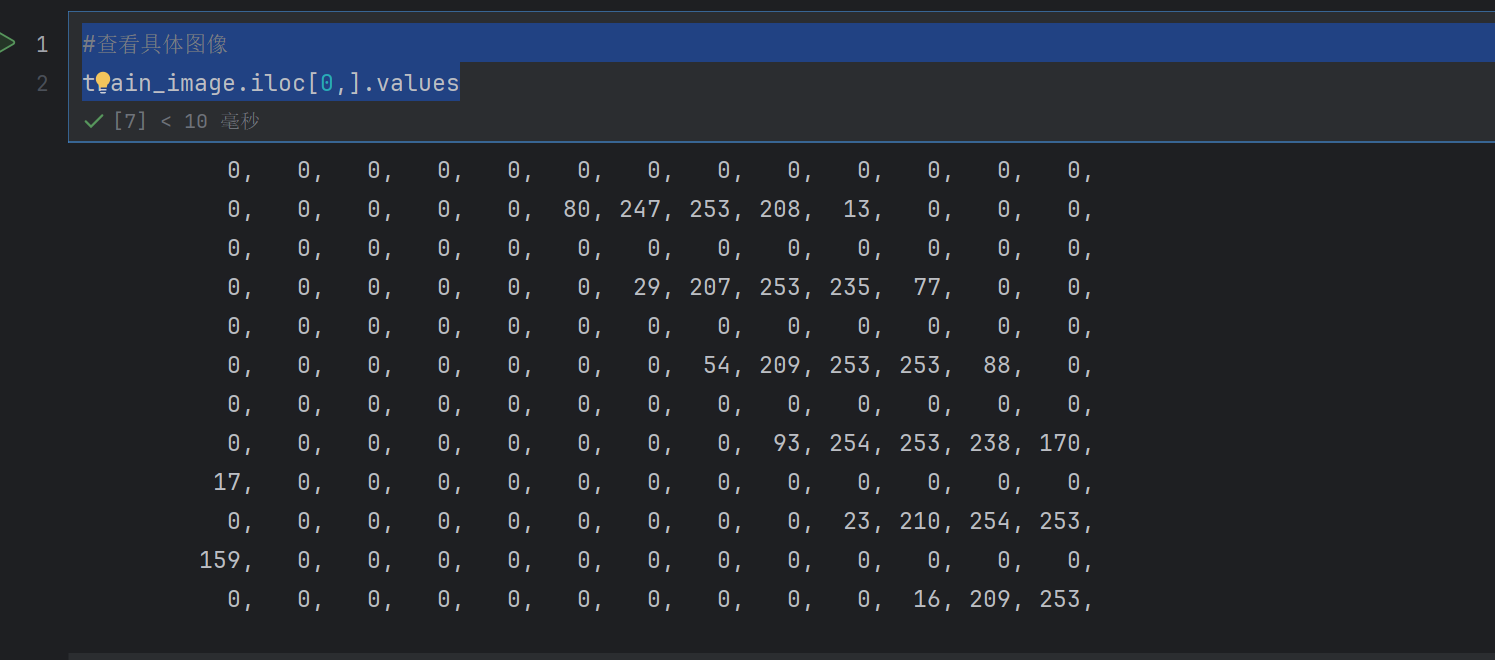
这是第一行
#查看具体图像
num=train_image.iloc[0,].values.reshape(28,28)
变成28行28列
plt.imshow(num)
plt.axis('off')
plt.show()
plt.imshow(num)
imshow 是 Matplotlib 中用于显示图像的核心函数。
参数 num 通常是一个数值数组(可以是二维数组或三维数组):
若为二维数组,会被当作灰度图像处理,数组中的每个值代表对应位置的像素亮度。
若为三维数组(形状为 (高度,宽度,3) 或 (高度,宽度,4)),则会被当作彩色图像(RGB 或 RGBA 格式),最后一个维度代表颜色通道。
plt.axis(‘off’)
这行代码用于隐藏图像的坐标轴(包括刻度、标签和边框),让图像显示更简洁,尤其适合纯粹展示图像内容的场景。
若不添加此行,图像周围会默认显示 x 轴和 y 轴的刻度与边框。
def to_plot(n):num=train_image.iloc[n,].values.reshape(28,28)plt.imshow(num)plt.axis('off')plt.show()
#数据基本处理
#对特征值归一化,,,变为0~1范围意思就是
train_image=train_image/255
train_image
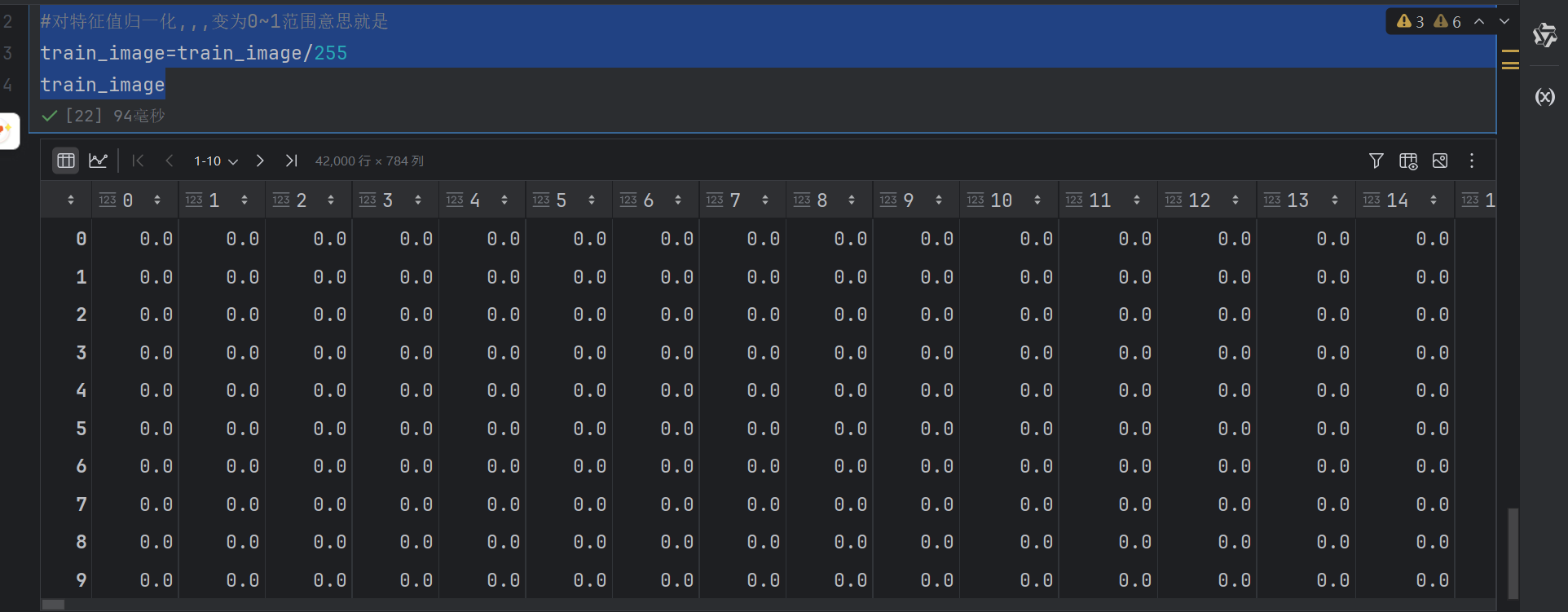
全部就都是零点几了
label目标值就是这一行表示的是数字几
train_label = train_label.values
这样目标值就变为一维的了
线性归一化(Min-Max 归一化)
这是最直观的归一化方法,核心是将原始数据线性映射到 [0, 1] 或 [-1, 1] 的固定区间内。
标准化(Z-Score 归一化)
标准化是将数据转换为 “均值为 0、标准差为 1” 的正态分布(或近似正态分布),属于一种 “基于统计特性” 的归一化。
#数据集分割
x_train,x_val,y_train,y_val = train_test_split(train_image,train_label,test_size=0.2,random_state=0)
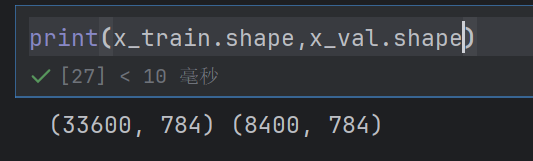
#特征降维--》特征太多了,模型训练
#多次使用pca,确定最后最优模型--->特征值合并
import time
from sklearn.decomposition import PCA
def n_component_analysis(n,x_train,x_val,y_train,y_val):start = time.time()#pca降维#n_components=n表示保留多少信息pca = PCA(n_components=n)print('开始降维......,传递的参数为;{}',format(n))pca.fit(x_train)x_train_pca = pca.transform(x_train)x_val_pca = pca.transform(x_val)#利用svc进行训练print('开始训练......')ss=svm.SVC()ss.fit(x_train_pca,y_train)#获取accuracyaccuracy=ss.score(x_val_pca,y_val)#记录结束时间end = time.time()print('准确率:{},耗时:{}'.format(accuracy,(end-start)))return accuracy
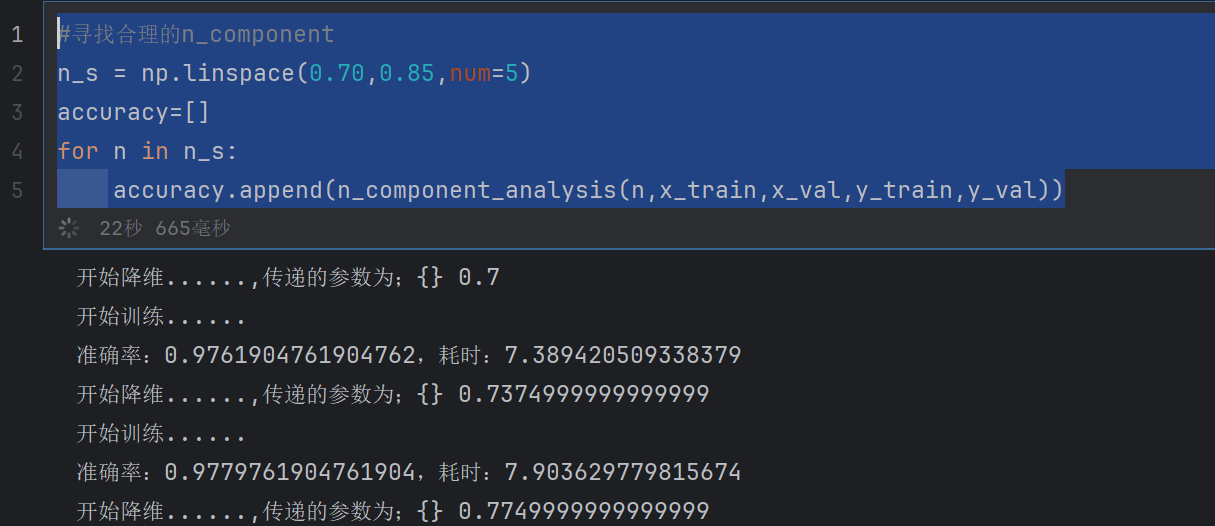
#寻找合理的n_component
n_s = np.linspace(0.70,0.85,num=5)
accuracy=[]
for n in n_s:accuracy.append(n_component_analysis(n,x_train,x_val,y_train,y_val))
#准确率可视化
plt.plot(n_s,np.array(accuracy),"r")
plt.show()
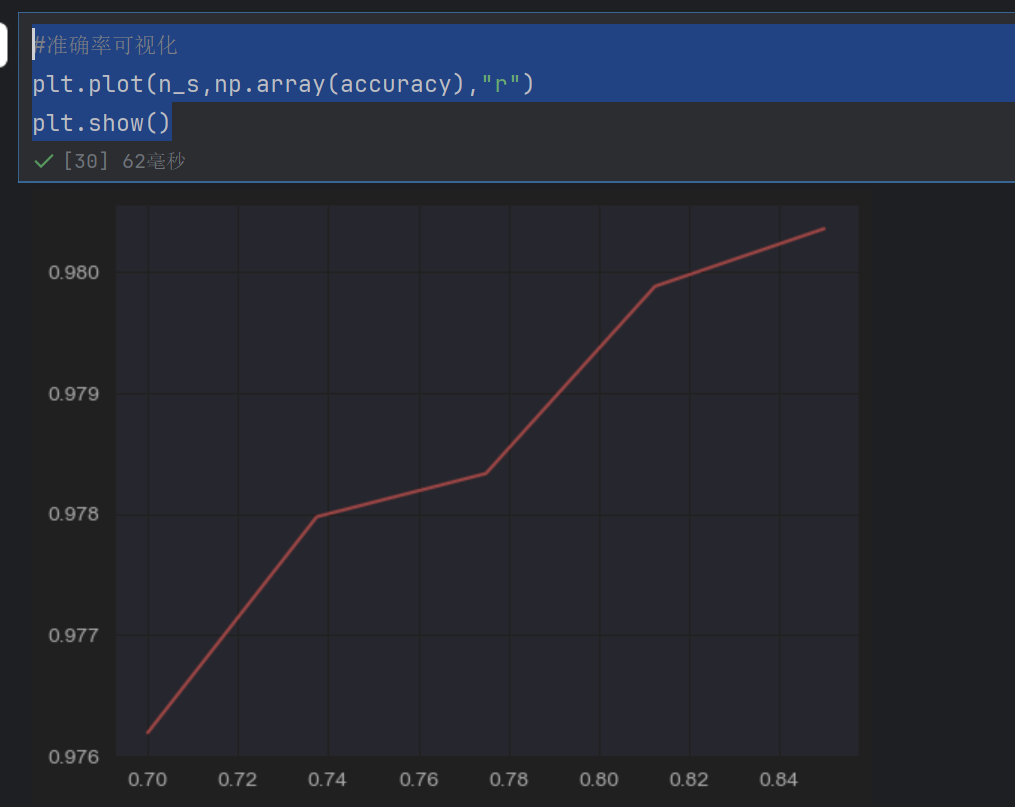
虽然准确率在上升,但是耗时也会增加的
我们这里选择n_component=0.8应该可以
#确定最优模型
pca = PCA(n_components=0.8)
pca.fit(x_train)
pca.n_components_
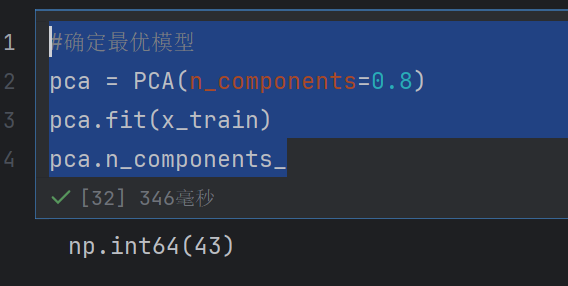
我们看到只有43个特征了
x_train_pca=pca.transform(x_train)
x_val_pca=pca.transform(x_val)
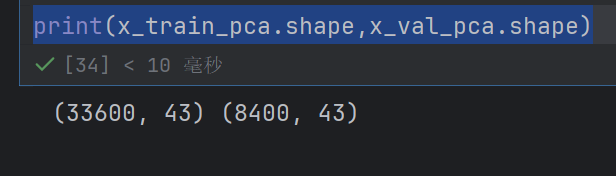
#训练模型,计算accurycy
ss1=svm.SVC()
ss1.fit(x_train_pca,y_train)
ss1.score(x_val_pca,y_val)