【控制理论】#3 一阶系统与二阶系统的时域响应分析

系统的时域响应分析研究一个系统在受到一个输入信号后，其输出信号随时间变化的规律和特性。

一阶系统的时域响应分析

一个典型的一阶系统微分方程为

$$\frac{\mathrm{d}x(t)}{\mathrm{d}t}+ax(t)=bu(t)$$

在零初始条件下对其进行拉普拉斯变换可得

$$sX(s)+aX(s)=bU(s)$$

则该系统的传递函数为

$$G(s)=\frac{X(s)}{U(s)}=\frac{b}{s+a}$$

单位冲激响应

单位冲激响应能够最直观地揭示系统固有的动态特性，是分析系统稳定性和响应速度的重要依据。在第一篇中我们介绍过单位冲激函数的定义如下

$$\{\begin{array}{c}\delta (t)=0,t\ne 0\\ {\int }_{-\infty }^{\infty }\delta (t)\mathrm{d}t=1\end{array}$$

其拉普拉斯变换为

$$\mathcal{L}[\delta (t)]={\int }_0^{\infty }\delta (t)e^{-st}\mathrm{d}t=e^{-s0}=1$$

当系统的输入为单位冲激函数时，$u(t)=\delta (t),U(s)=1$，则输出的拉普拉斯变换为

$$X(s)=U(s)G(s)=\frac{b}{s+a}$$

应用拉普拉斯逆变换得

$$x(t)={\mathcal{L}}^{-1}[X(s)]={\mathcal{L}}^{-1}\left[\frac{b}{s+a}\right]=b{e}^{-at}$$

于是我们可画出一阶系统的单位冲激响应图像

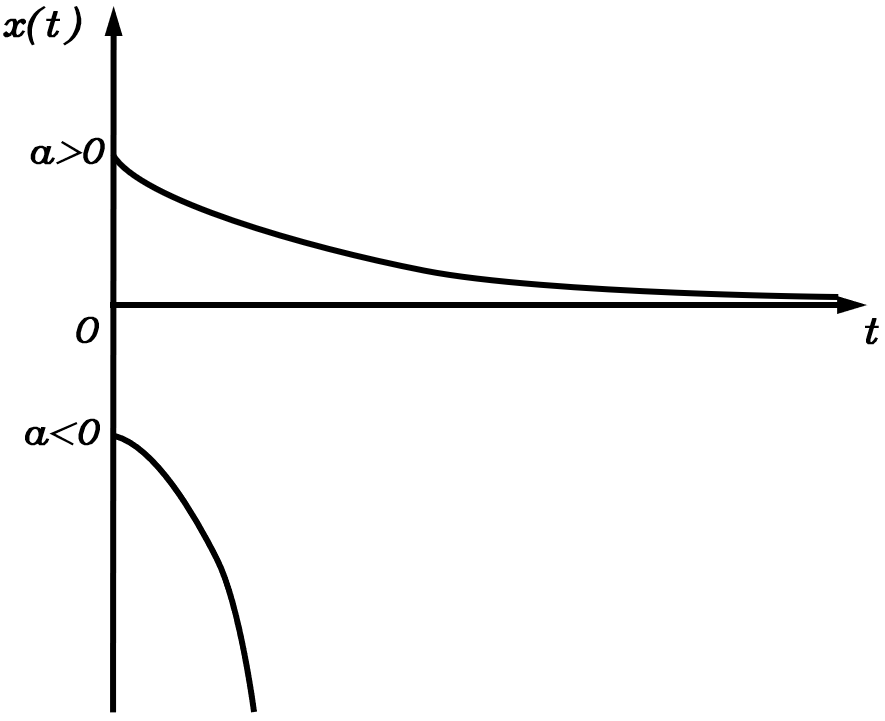
对于非零初始条件的零输入响应，即$u(0)=0,x(0)=x_0\ne 0$，则系统微分方程及其拉普拉斯变换变为

$$\begin{array}{c}\frac{\mathrm{d}x(t)}{\mathrm{d}t}+ax(t)=0\\ sX(s)-x_0+aX(s)=0\end{array}$$

系统输出的拉普拉斯变换及逆变换结果为

$$\begin{array}{c}X(s)=\frac{x_0}{s+a}\\ x(t)={\mathcal{L}}^{-1}[X(s)]=x_0{e}^{-at}\end{array}$$

则一阶系统的初始条件响应曲线为

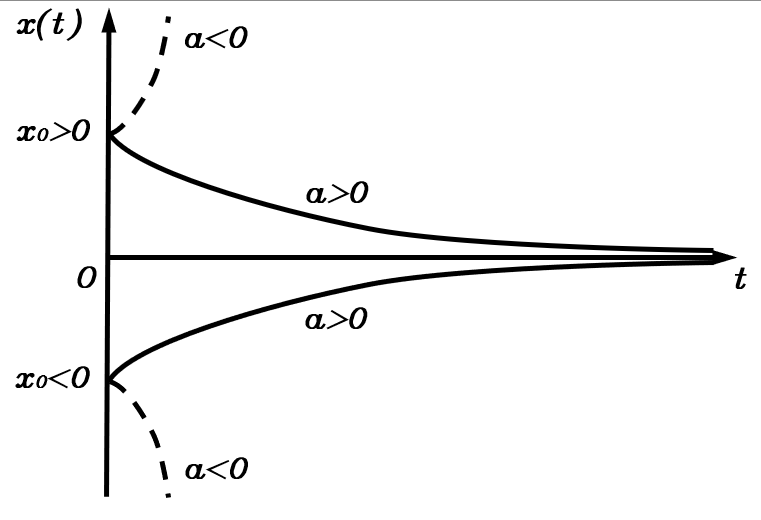
由此可见，一阶系统对初始条件的响应即系统的冲激响应，冲激强度决定系统的初始输出，而输出的收敛或发散取决于$a$的符号。

单位阶跃响应

单位阶跃函数的数学表达式为

$$u(t)=\{\begin{array}{c}1,t⩾0\\ 0,t<0\end{array}$$

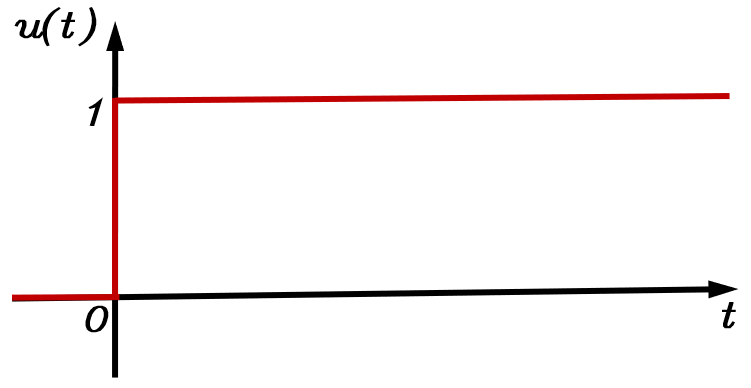
单位阶跃响应能够非常全面地展示系统的各项性能指标。当系统的输入为单位阶跃函数时，$U(s)=\frac{1}{s}$，则系统输出的拉普拉斯变换及其逆变换结果为

$$\begin{array}{c}X(s)=U(s)G(s)=\frac{b}{s(s+a)}\\ x(t)={\mathcal{L}}^{-1}[X(s)]={\mathcal{L}}^{-1}\left[\frac{b}{a}\left(\frac{1}{s}-\frac{1}{s+a}\right)\right]=\frac{b}{a}(1-e^{-at})\end{array}$$

当$a<0$时，$x(t)$将趋于负无穷。当$a>0$时，一阶系统的单位阶跃响应曲线为

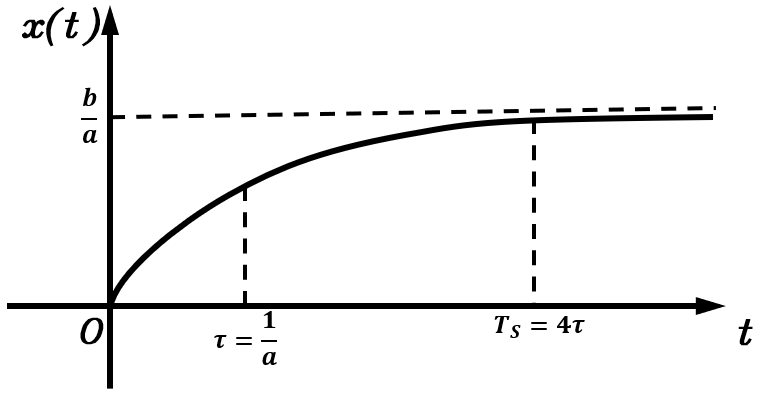
$x(t)$从$0$开始随着时间的增加而不断地增加，直到达到稳定值$\frac{b}{a}$。在这个过程中有两个一阶系统的重要性能指标

• 时间常数：$\tau =\frac{1}{a}$，此时$x(\tau )\approx 0.63\frac{b}{a}$。这个参数反映了系统的响应速度，$a$越大，$\tau$越小，系统的响应速度越快。
• 稳定时间：$T_S=4\tau =\frac{4}{a}$，此时$x(T_S)\approx 0.98\frac{b}{a}$。它表示了系统输出与终值之间的差距达到$2\%$以内所需要的事件，在工程中可以理解为对系统施加一个阶跃输入后，系统需要$T_S$的时间达到稳定状态。

在具体工程案例中，如果确定了一阶系统的终值，可以通过实验的方法测量上述指标来确定一阶系统的参数。

二阶系统的时域响应分析

以下面这个弹簧质量阻尼系统为例（$k,b,m>0$）

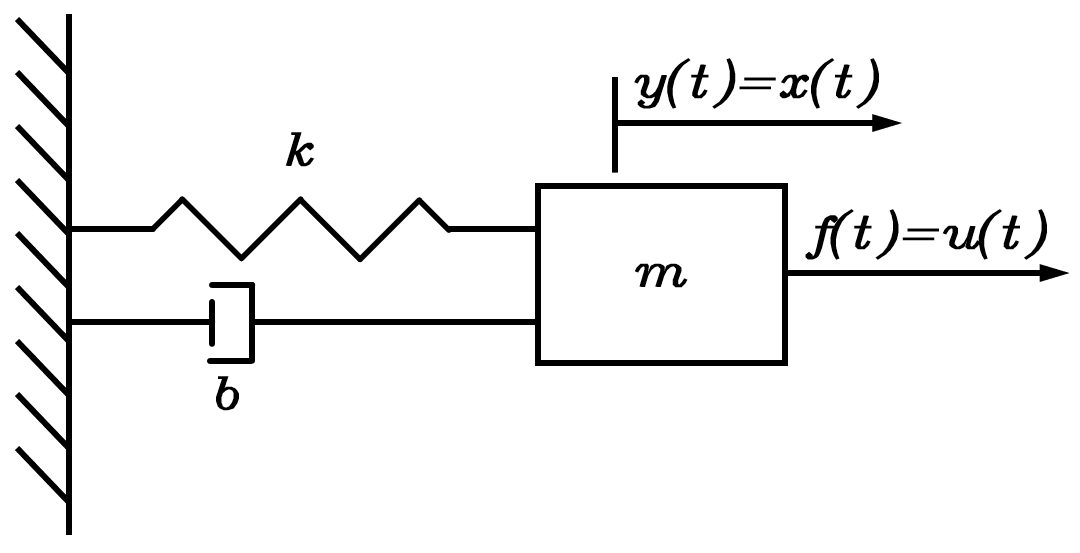
其对应的微分方程为

$$m\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}+b\frac{\mathrm{d}x(t)}{\mathrm{d}t}+kx(t)=f(t)$$

调整可得

$$\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}+\frac{b}{m}\frac{\mathrm{d}x(t)}{\mathrm{d}t}+\frac{k}{m}x(t)=\frac{1}{m}f(t)$$

定义

• 固有频率：${\omega }_n=\sqrt{\frac{k}{m}}$
• 阻尼比：$\zeta =\frac{b}{2\sqrt{km}}$

代入得

$$\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}+2\zeta {\omega }_n\frac{\mathrm{d}x(t)}{\mathrm{d}t}+{\omega }_n^{2}x(t)=\frac{1}{m}f(t)$$

为了简化计算，定义系统的输入$u(t)=\frac{f(t)}{m{\omega }_n^2}$，代入上式得

$$\frac{{\mathrm{d}}^{2}x(t)}{\mathrm{d}{t}^2}+2\zeta {\omega }_n\frac{\mathrm{d}x(t)}{\mathrm{d}t}+{\omega }_n^{2}x(t)={\omega }_n^{2}u(t)$$

考虑零初始状态，对上式两边进行拉普拉斯变换并整理可得其传递函数为

$$G(s)=\frac{X(s)}{U(s)}=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$

如果使用状态空间方程的表达形式，则设系统的状态变量为$\mathbf{z}(t)=[z_1(t),z_2(t){]}^{\top }={\left[x(t,\frac{\mathrm{d}x(t)}{\mathrm{d}t})\right]}^{\top }$，得到

$$\begin{array}{rl}\frac{\mathrm{d}{z}_1(t)}{\mathrm{d}t}=& z_2(t)\\ \frac{\mathrm{d}{z}_2(t)}{\mathrm{d}t}=& \frac{{\mathrm{d}}^2{z}_1(t)}{\mathrm{d}{t}^2}=-2\zeta {\omega }_n{z}_2(t)-{\omega }_n^2{z}_1(t)+{\omega }_n^{2}u(t)\end{array}$$

将其写成紧凑的矩阵形式得到

$$\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=\mathbf{Az}(t)+\mathbf{B}u(t)$$

其中

$$\mathbf{A}=\left[\begin{array}{cc}0& 1\\ -{\omega }_n^2& -2\zeta {\omega }_n\end{array}\right],\mathbf{B}=\left[\begin{array}{c}0\\ {\omega }_n^2\end{array}\right]$$

初始状态响应

本节采用状态空间方程的相轨迹法定性分析系统对初始条件的响应，即系统在无输入情况下，$t=0$时刻质量块的位置$x(0)\ne 0$或速度${\frac{\mathrm{d}x(t)}{\mathrm{d}t}|}_{t=0}\ne 0$的响应。

当系统的输入$u(t)=0$时，系统的状态空间方程可写成

$$\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=\mathbf{Az}(t),\mathbf{A}=\left[\begin{array}{cc}0& 1\\ -{\omega }_n^2& -2\zeta {\omega }_n\end{array}\right]$$

求该系统的平衡点，令$\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=0$可得$z_{1f}=z_{2f}=0$。

分析平衡点的性质需得到状态矩阵$\mathbf{A}$的特征值，令$|\mathbf{A}-\lambda \mathbf{I}|=0$得

$$\left|\begin{array}{cc}-\lambda & 1\\ -{\omega }_n^2& -2\zeta {\omega }_n-\lambda \end{array}\right|={\lambda }^2+2\zeta {\omega }_n\lambda +{\omega }_n^2=0$$

$$\{\begin{array}{c}{\lambda }_1=-\zeta {\omega }_n+{\omega }_n\sqrt{{\zeta }^2-1}\\ {\lambda }_2=-\zeta {\omega }_n-{\omega }_n\sqrt{{\zeta }^2-1}\end{array}$$

情况一：$\zeta ⩾1$

此时${\lambda }_1,{\lambda }_2$均为实数且都小于零，根据上一篇可知平衡点${\mathbf{z}}_f=[0,0{]}^{\top }$是一个稳定节点，相轨迹如下图所示

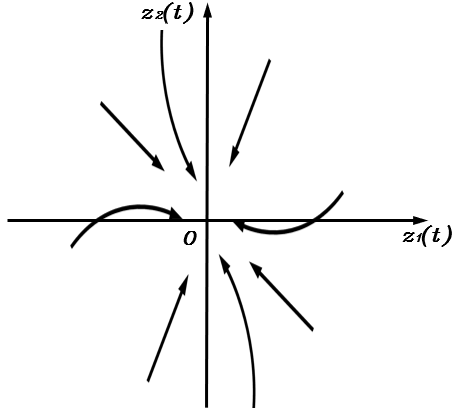
不管初始位置从何处开始，系统能量都会随着时间的增加而趋于零。其中，当$\zeta >1$时的系统称为过阻尼系统，当$\zeta =1$时的系统称为临界阻尼系统，二者的区别在于临界阻尼系统收敛更快。

情况二：$0<\zeta <1$

此时$\sqrt{{\zeta }^2-1}=\sqrt{1-{\zeta }^2}\mathrm{j}$，则有

$$\{\begin{array}{c}{\lambda }_1=-\zeta {\omega }_n+{\omega }_n\sqrt{1-{\zeta }^2}\mathrm{j}\\ {\lambda }_2=-\zeta {\omega }_n-{\omega }_n\sqrt{1-{\zeta }^2}\mathrm{j}\end{array}$$

${\lambda }_1,{\lambda }_2$为一对实部小于零的共轭复数，上一篇未提到这种情况。对于${\lambda }_{1,2}=\sigma \pm \mathrm{j}\omega$，则分析状态方程解耦后新状态变量

$$\frac{\mathrm{d}\bar{\mathbf{z}}(t)}{\mathrm{d}t}=\left[\begin{array}{cc}\sigma +\mathrm{j}\omega & 0\\ 0& \sigma -\mathrm{j}\omega \end{array}\right]\bar{\mathbf{z}}(t)$$

$$\bar{\mathbf{z}}(t)=\left[\begin{array}{c}{C}_1{e}^{(\sigma +\mathrm{j}\omega )t}\\ C_2{e}^{(\sigma -\mathrm{j}\omega )t}\end{array}\right]=e^{\sigma t}\left[\begin{array}{c}{C}_1{e}^{\mathrm{j}\omega t}\\ C_2{e}^{-\mathrm{j}\omega t}\end{array}\right]$$

该相轨迹在实部平面上的投影为螺旋线，$\sigma$的正负决定了系数$e^{\sigma t}$随时间增加而增大还是趋于零。当$\sigma >0$时，$\bar{\mathbf{z}}(t)$的相轨迹为从平衡点向外发散的螺旋线，平衡点称为不稳定焦点；当$\sigma <0$时，$\bar{\mathbf{z}}(t)$的相轨迹为向内收敛到平衡点的螺旋线，平衡点称为稳定焦点。

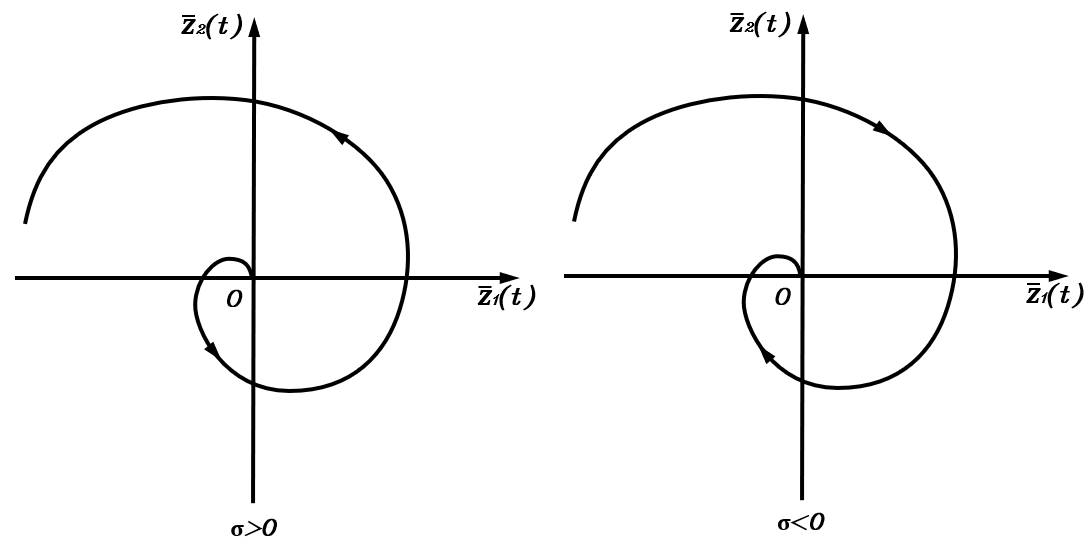
原状态变量$\mathbf{z}(t)$的相轨迹只是在此基础上经过了线性变换，变化趋势相同。对于弹簧阻尼系统而言，其相轨迹是类似右图的螺旋线，即边振荡边衰减，这种系统称为欠阻尼系统。

情况三：$\zeta =0$

此时${\lambda }_{1,2}=\pm {\omega }_n\mathrm{j}$，根据上一篇可知平衡点${\mathbf{z}}_f=[0,0{]}^{\top }$是一个中心点，相轨迹如下图所示

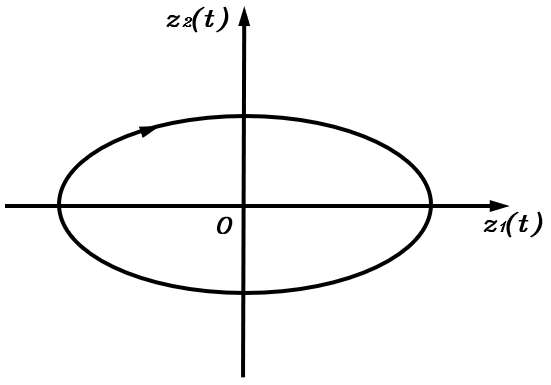
质量块将会不断地振动，循环往复，总能量不会被消耗，这种系统称为无阻尼系统。

单位阶跃响应

本节采用传递函数的方法定量分析二阶系统的单位阶跃响应。当系统的输入为单位阶跃函数时，输入的拉普拉斯变换为$U(s)=\frac{1}{s}$，可求出系统输出的拉普拉斯变换为

$$X(s)=G(s)U(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}\times \frac{1}{s}$$

令分母为零可求出系统的三个极点分别为

$$\{\begin{array}{rl}{s}_{p1}& =0\\ s_{p2}& =-\zeta {\omega }_n+{\omega }_n\sqrt{{\zeta }^2-1}\\ s_{p3}& =-\zeta {\omega }_n-{\omega }_n\sqrt{{\zeta }^2-1}\end{array}$$

不同的$\zeta$值将对应不同的系统表现，本节以欠阻尼系统$0<\zeta <1$这个最复杂的情况为例，此时系统的极点变为

$$\{\begin{array}{rl}{s}_{p1}& =0\\ s_{p2}& =-\zeta {\omega }_n+{\omega }_n\sqrt{1-{\zeta }^2}\mathrm{j}\\ s_{p3}& =-\zeta {\omega }_n-{\omega }_n\sqrt{1-{\zeta }^2}\mathrm{j}\end{array}$$

接下来采用分式分解法求$X(s)$的拉普拉斯逆变换，设三个待定的分子系数分别为$A,B,C$，可得

$$\begin{array}{rl}X(s)& =\frac{{\omega }_n^2}{s(s^2+2\zeta {\omega }_{n}s+{\omega }_n^2)}=\frac{A}{s-s_{p1}}+\frac{B}{s-s_{p2}}+\frac{C}{s-s_{p3}}\\ & =\frac{A(s-s_{p2})(s-s_{p3})+B(s-s_{p1})(s-s_{p3})+C(s-s_{p1})(s-s_{p2})}{(s-s_{p1})(s-s_{p2})(s-s_{p3})}\end{array}$$

取等式两侧分子

$${\omega }_n^2=A(s-s_{p2})(s-s_{p3})+B(s-s_{p1})(s-s_{p3})+C(s-s_{p1})(s-s_{p2})$$

分别令$s=s_{p1},s_{p2},s_{p3}$可利用上式求出三个系数如下

$$\{\begin{array}{rl}A& =1\\ B& =-\frac{1}{2}(1-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})\\ C& =-\frac{1}{2}(1-\frac{\zeta }{\sqrt{1+{\zeta }^2}}\mathrm{j})\end{array}$$

于是$X(s)$的分式分解结果为

$$X(s)=\frac{1}{s-s_{p1}}-\frac{1}{2}(1-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})\frac{1}{s-s_{p2}}-\frac{1}{2}(1+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})\frac{1}{s-s_{p3}}$$

其拉普拉斯逆变换为

$$x(t)={\mathcal{L}}^{-1}[X(s)]=e^{s_{p1}t}-\frac{1}{2}(1-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})e^{s_{p2}t}-\frac{1}{2}(1+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})e^{s_{p3}t}$$

将极点的值代入得

$$x(t)=1-e^{-\zeta {\omega }_{n}t}\left[\frac{1}{2}(1-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})e^{{\omega }_n\sqrt{1-{\zeta }^2}\mathrm{j}t}-\frac{1}{2}(1+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})e^{-{\omega }_n\sqrt{1-{\zeta }^2}\mathrm{j}t}\right]$$

定义系统的阻尼固有频率为${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$，即极点$s_{p2,p3}$的虚部。此时上式可化简为

$$\begin{array}{rl}x(t)& =1-e^{-\zeta {\omega }_{n}t}\left[\frac{1}{2}(1-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})e^{{\omega }_d\mathrm{j}t}-\frac{1}{2}(1+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j})e^{-{\omega }_d\mathrm{j}t}\right]\\ & =1-e^{-\zeta {\omega }_{n}t}\left[\frac{1}{2}(e^{{\omega }_d\mathrm{j}t}+e^{-{\omega }_d\mathrm{j}t})+\frac{1}{2}\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{j}(-e^{{\omega }_d\mathrm{j}t}+e^{-{\omega }_d\mathrm{j}t})\right]\end{array}$$

根据欧拉公式，$e^{{\omega }_d\mathrm{j}t}=\cos {\omega }_{d}t+\mathrm{j}\sin {\omega }_{d}t$，$e^{-{\omega }_d\mathrm{j}t}=\cos {\omega }_{d}t-\mathrm{j}\sin {\omega }_{d}t$，可得

$$\begin{array}{r}\frac{1}{2}(e^{{\omega }_d\mathrm{j}t}+e^{-{\omega }_d\mathrm{j}t})=\cos {\omega }_{d}t\\ \frac{1}{2}\mathrm{j}(-e^{{\omega }_d\mathrm{j}t}+e^{-{\omega }_d\mathrm{j}t})=\sin {\omega }_{d}t\end{array}$$

代回原式化简得到

$$x(t)=1-e^{-\zeta {\omega }_{n}t}\left[\cos {\omega }_{d}t+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\sin {\omega }_{d}t\right]$$

令$\phi =\arctan \frac{\sqrt{1-{\zeta }^2}}{\zeta }$，可得

$$\begin{array}{rl}\cos {\omega }_{d}t+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\sin {\omega }_{d}t& =\sqrt{1^2+{\left(\frac{\zeta }{\sqrt{1-{\zeta }^2}}\right)}^2}\sin ({\omega }_{d}t+\phi )\\ & =\sqrt{\frac{1}{1-{\zeta }^2}}\sin ({\omega }_{d}t+\phi )\end{array}$$

代回原式化简得到

$$x(t)=1-e^{-\zeta {\omega }_{n}t}\sqrt{\frac{1}{1-{\zeta }^2}}\sin ({\omega }_{d}t+\phi )$$

上式即为二阶欠阻尼系统单位阶跃响应的时间函数，其中“1”来自系统输入，后半部分的$e^{-\zeta {\omega }_{n}t}\sqrt{\frac{1}{1-{\zeta }^2}}\sin ({\omega }_{d}t+\phi )$是一个指数衰减的三角函数，综合来看$x(t)$的图像如下

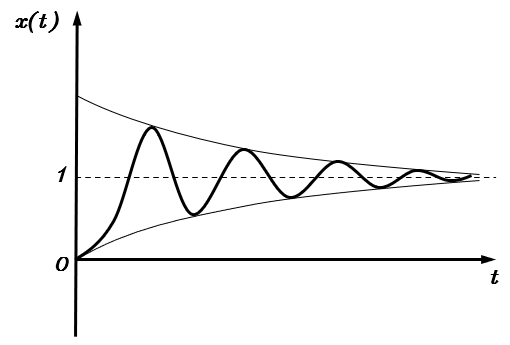
同样的方法可以用于推导其他情况，这里直接给出结果

• 无阻尼：$x(t)=1-\cos {\omega }_{n}t$
• 临界阻尼：$x(t)=1-e^{-{\omega }_{n}t}(1+{\omega }_{n}t)$
• 过阻尼：$x(t)=1-\frac{1}{2\sqrt{{\zeta }^2-1}(\zeta -\sqrt{{\zeta }^2-1})}{e}^{(-\zeta +\sqrt{{\zeta }^2-1}){\omega }_{n}t}+\frac{1}{2\sqrt{{\zeta }^2-1}(\zeta +\sqrt{{\zeta }^2-1})}{e}^{(-\zeta -\sqrt{{\zeta }^2-1}){\omega }_{n}t}$

二阶系统的性能指标分析

弹簧阻尼系统是控制领域最基础的物理模型之一，其描述了一个系统的两种基本动态特性

• 惯性/弹性（弹簧系数$k$）：代表系统存储和释放能量的能力，倾向于使系统振荡。
• 耗散/阻力（阻尼系数$b$）：代表系统消耗能量的能力，倾向于使系统稳定下来，抑制振荡。

下面以上一节求出的欠阻尼单位阶跃响应函数为例，介绍该系统的一些重要的性能指标

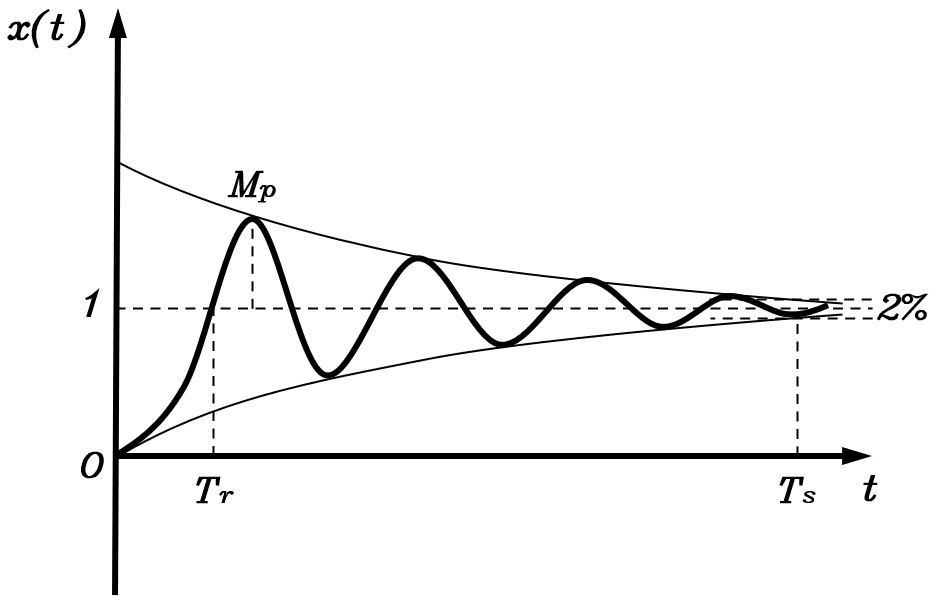
上升时间$T_r$：系统第一次到达稳定点的时间，体现了系统的反应速度。对于达不到稳定点的系统取稳定值的$90\%$。

根据定义，$x(T_r)=1$，代入函数表达式得

$$\begin{array}{rl}1& =1-e^{-\zeta {\omega }_n{T}_r}\sqrt{\frac{1}{1-{\zeta }^2}}\sin ({\omega }_d{T}_r+\phi )\\ 0& =e^{-\zeta {\omega }_n{T}_r}\sqrt{\frac{1}{1-{\zeta }^2}}\sin ({\omega }_d{T}_r+\phi )\end{array}$$

由于$e^{-\zeta {\omega }_n{T}_r}\sqrt{\frac{1}{1-{\zeta }^2}}\ne 0$，故等式成立时只有$\sin ({\omega }_d{T}_r+\phi )=0$，得到

$$\begin{array}{r}{\omega }_d{T}_r+\phi =k\pi ,k=1,2,3,\cdots \\ T_r=\frac{k\pi -\phi }{{\omega }_d},k=1,2,3,\cdots \end{array}$$

第一次达到稳定点的时间取$k=1$得

$$T_r=\frac{\pi -\phi }{{\omega }_d}=\frac{\pi -\phi }{{\omega }_n\sqrt{1-{\zeta }^2}}$$

上式说明，固有频率${\omega }_n$越大或阻尼比$\zeta$越小，上升时间$T_r$越小，系统的响应就越快。

最大超调量$M_p$：系统输出的最大值与稳态值的相对误差，即$M_p=\frac{x_{\max }-x(\infty )}{x(\infty )}\times 100\%$，体现了系统的相对稳定性。

求解最大超调量首先要找到系统的峰值时间$T_p$，在此时刻有

$$\begin{array}{rl}{\frac{\mathrm{d}x(t)}{\mathrm{d}t}|}_{t=T_p}& =e^{-\zeta {\omega }_n{T}_p}\sqrt{\frac{1}{1-{\zeta }^2}}(\zeta {\omega }_n\sin ({\omega }_d{T}_p+\phi )-{\omega }_d\cos ({\omega }_d{T}_p+\phi ))\\ & =0\end{array}$$

由于$e^{-\zeta {\omega }_n{T}_r}\sqrt{\frac{1}{1-{\zeta }^2}}\ne 0$，故等式成立时只有$\zeta {\omega }_n\sin ({\omega }_d{T}_r+\phi )-{\omega }_d\cos ({\omega }_d{T}_p+\phi )=0$，得到

$$\begin{array}{r}\zeta {\omega }_n\sin ({\omega }_d{T}_r+\phi )={\omega }_d\cos ({\omega }_d{T}_p+\phi )\\ \tan ({\omega }_d{T}_p+\phi )=\frac{{\omega }_d}{\zeta {\omega }_n}=\frac{\sqrt{1-{\zeta }^2}}{\zeta }\end{array}$$

根据上一小节定义，$\frac{\sqrt{1-{\zeta }^2}}{\zeta }=\tan \phi$，所以$\tan ({\omega }_d{T}_p+\phi )=\tan \phi$，即

$${\omega }_d{T}_p=k\pi ,k=1,2,3,\cdots$$

第一次峰值时间取$k=1$得

$$T_p=\frac{\pi }{{\omega }_d}=\frac{\pi }{{\omega }_n\sqrt{1-{\zeta }^2}}$$

将$T_p$代入系统输出函数得

$$x(T_p)=1+e^{-\frac{\zeta \pi }{\sqrt{1-{\zeta }^2}}}\sqrt{\frac{1}{1-{\zeta }^2}}\sin \phi$$

因为$\frac{\sqrt{1-{\zeta }^2}}{\zeta }=\tan \phi$，所以$\sin \phi =\sqrt{1-{\zeta }^2}$，代入上式得

$$x(T_p)=1+e^{-\frac{\zeta \pi }{\sqrt{1-{\zeta }^2}}}$$

则该系统的最大超调量为

$$M_p=\frac{1+e^{-\frac{\zeta \pi }{\sqrt{1-{\zeta }^2}}}-1}{1}\times 100\%=e^{-\frac{\zeta \pi }{\sqrt{1-{\zeta }^2}}}$$

上式说明，最大超调量只与阻尼比$\zeta$相关。$\zeta$越大，$M_p$就越小。

稳定时间$T_s$：系统进入稳态的误差范围内的时间，一般为最终状态的$2\%$以内，体现了系统的收敛速度。根据其定义可得

$$x(T_s)=1-e^{-\zeta {\omega }_n{T}_s}\sqrt{\frac{1}{1-{\zeta }^2}}\sin ({\omega }_d{T}_s+\phi )=0.98$$

考虑稳态时振动部分的最大值，即$\sin ({\omega }_d{T}_s+\phi )=1$，则上式变为

$$e^{-\zeta {\omega }_n{T}_s}\sqrt{\frac{1}{1-{\zeta }^2}}=0.02$$

对于较小的$\zeta$，$\sqrt{\frac{1}{1-{\zeta }^2}}\approx 1$，$T_s$可用如下近似公式计算

$$T_s\approx \frac{4}{\zeta {\omega }_n}$$

上式说明稳定时间与$\zeta {\omega }_n$（即系统极点$s_{p2,p3}$的实部）成反比。

与一阶系统中相同，上述指标也可以通过实验测得，进而用于系统的相关参数。

在设计系统时，通常情况下，我们无法要求系统的各项指标都达到优秀，尤其是在引入更多指标之后，需要结合应用场景优先考虑某些指标。对于追求精度与稳定的系统，应当注重最大超调量；而对于需要应对突发情况的场景，则上升时间会成为首选要素。